Download as PDF, PPTX
Uploaded bynipslab
COHERENCE, SELF-SIMILARITY AND BRAIN ACTIVITY
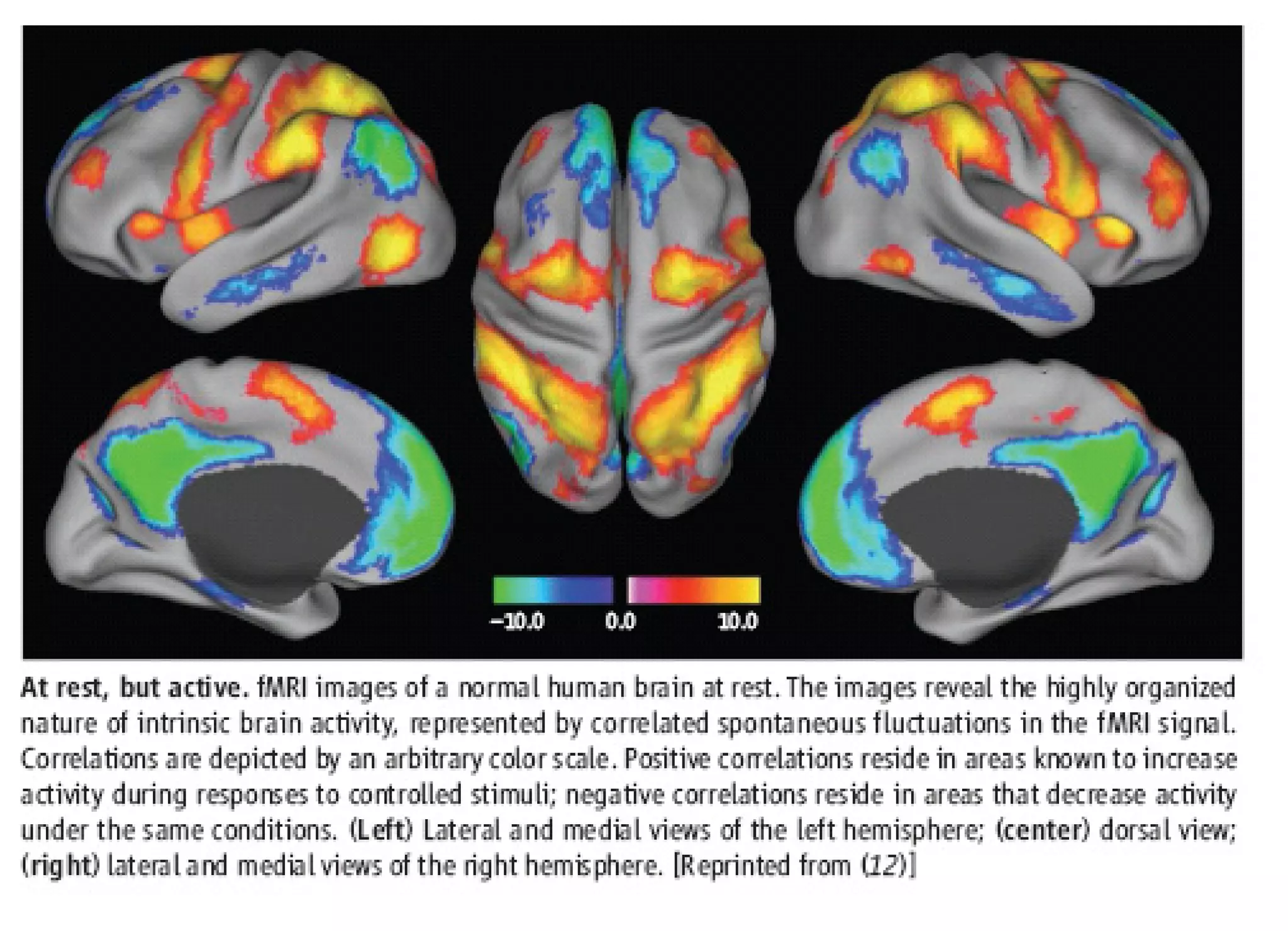
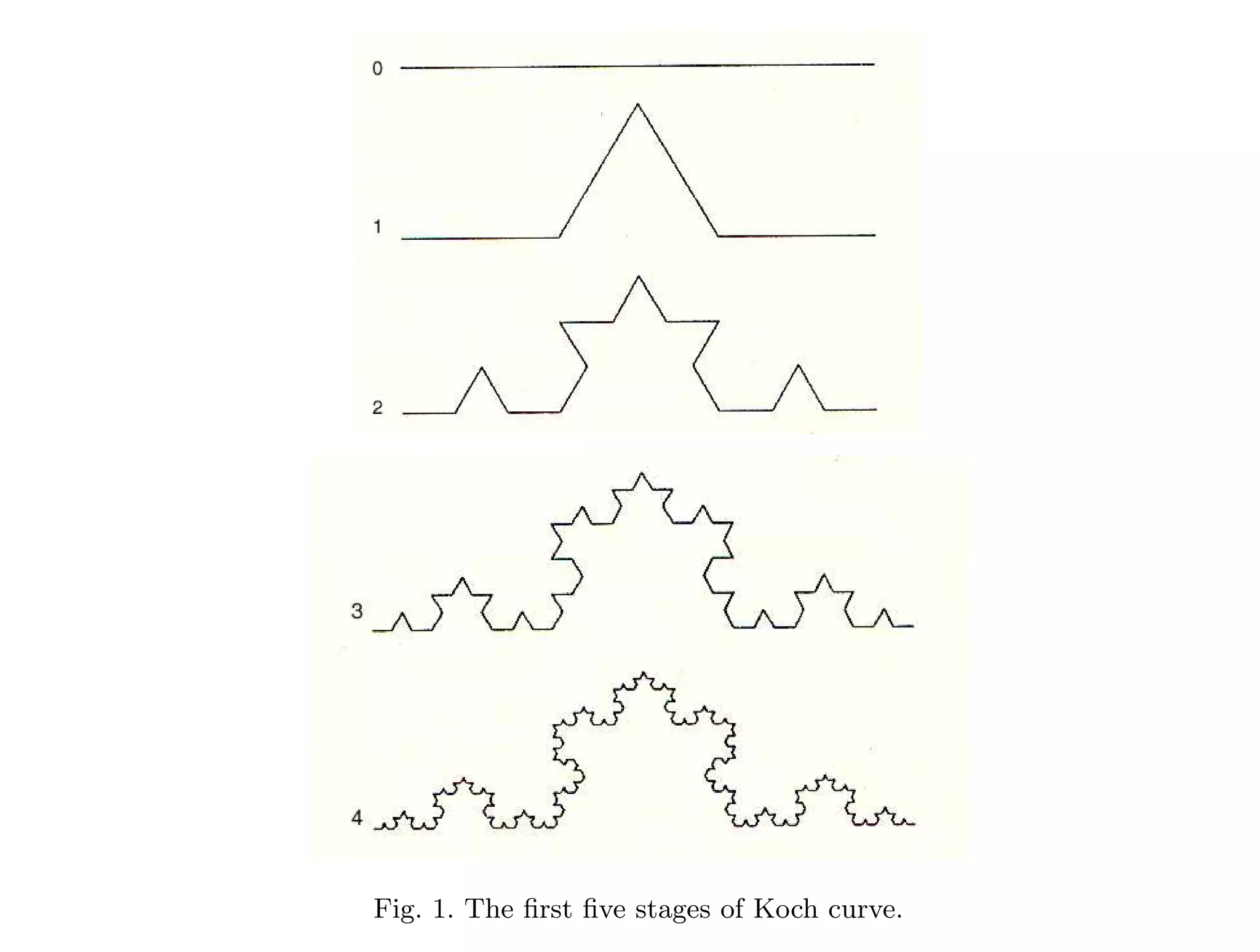
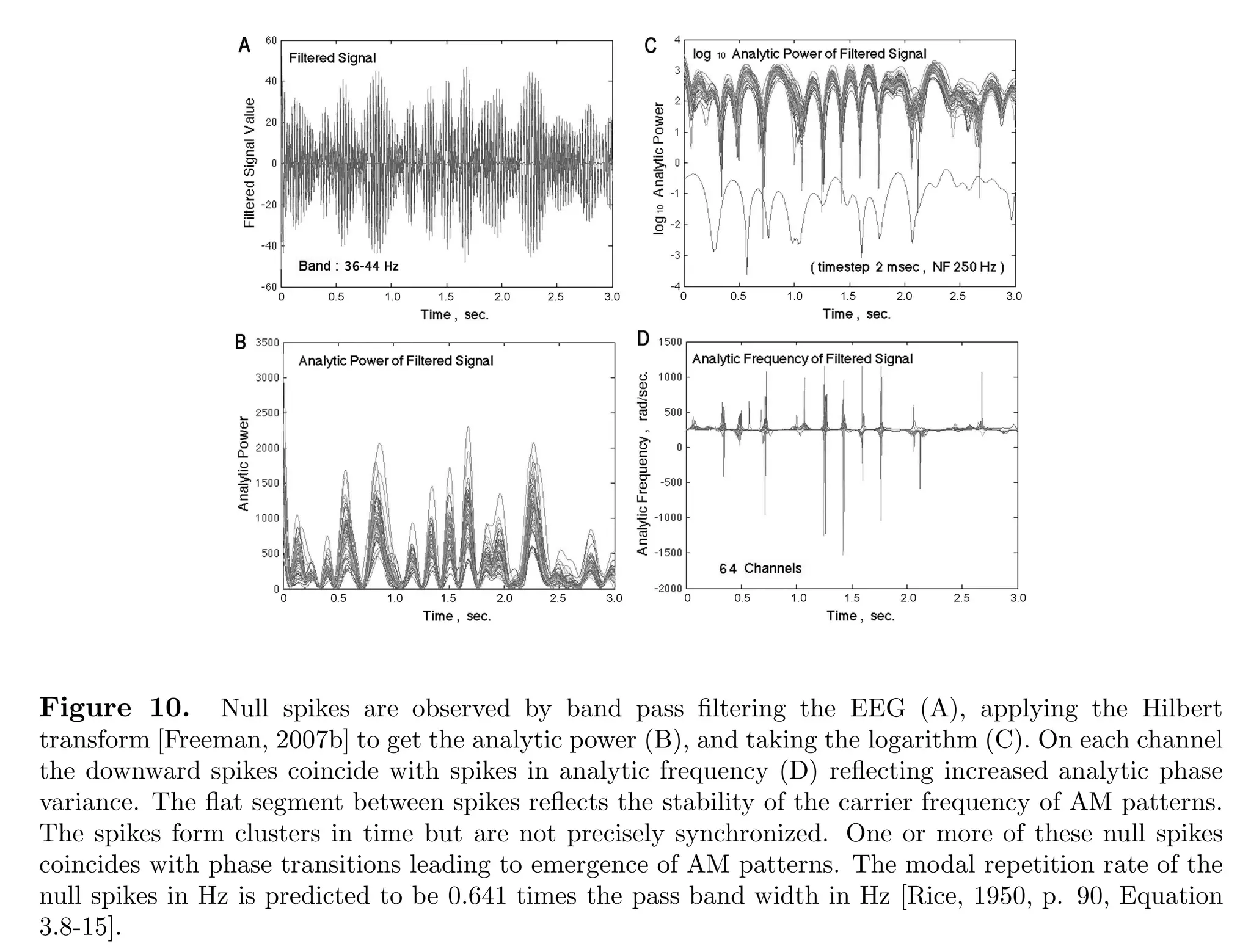
1) The document discusses coherence and self-similarity in brain activity, proposing that spatially extended domains of synchronized neural oscillations form rapidly in the brain and re-synchronize in frames at rates in the theta-alpha range. 2) These synchronized oscillation patterns cover large areas of the brain and are present during both resting and cognitive task periods, suggesting they represent background brain activity modulated by environmental engagement. 3) A dissipative quantum field theory model is able to account for the dynamical formation of these synchronized oscillations through spontaneous symmetry breaking mechanisms generating long-range correlations mediated by massless quanta.
