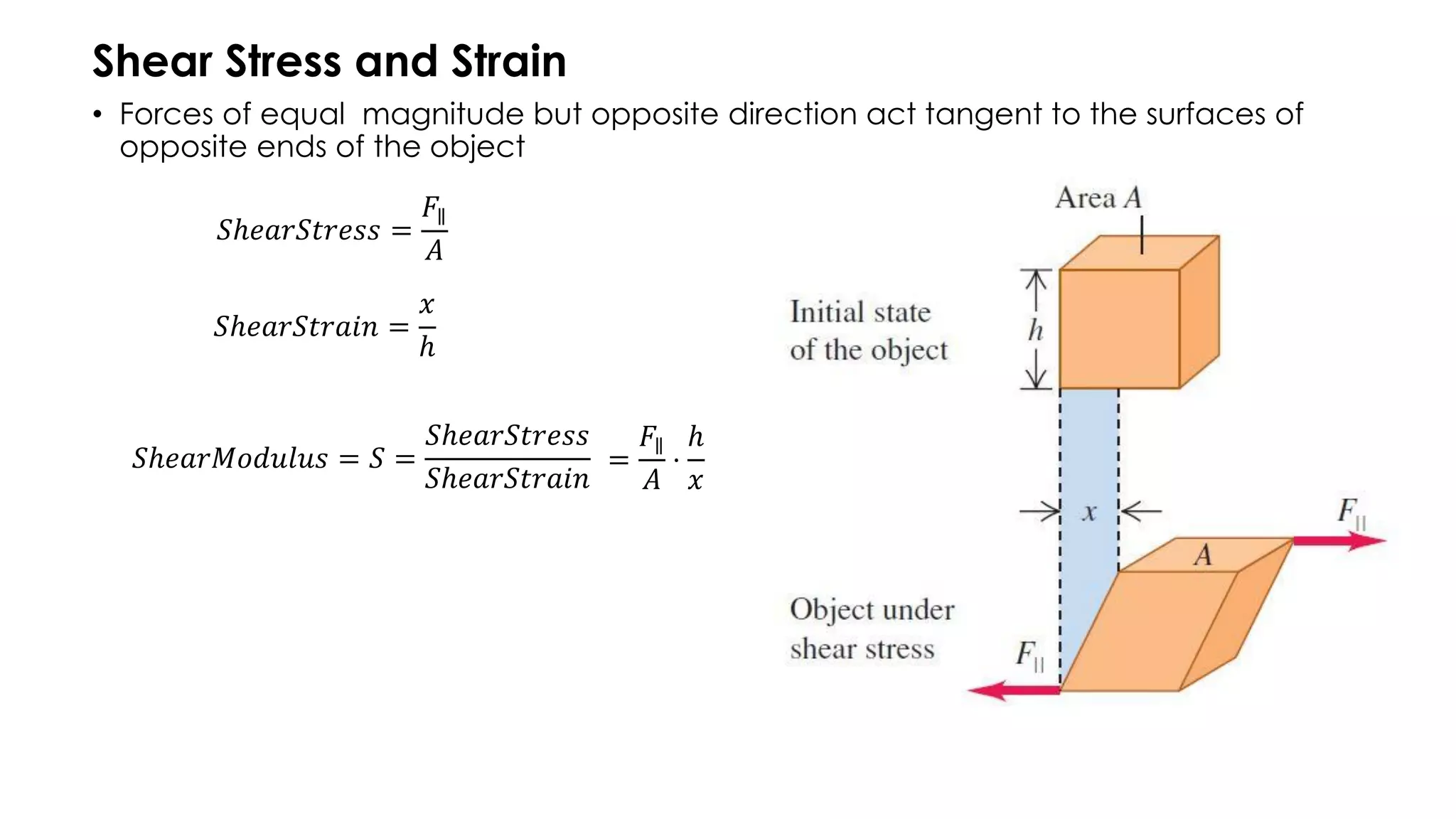
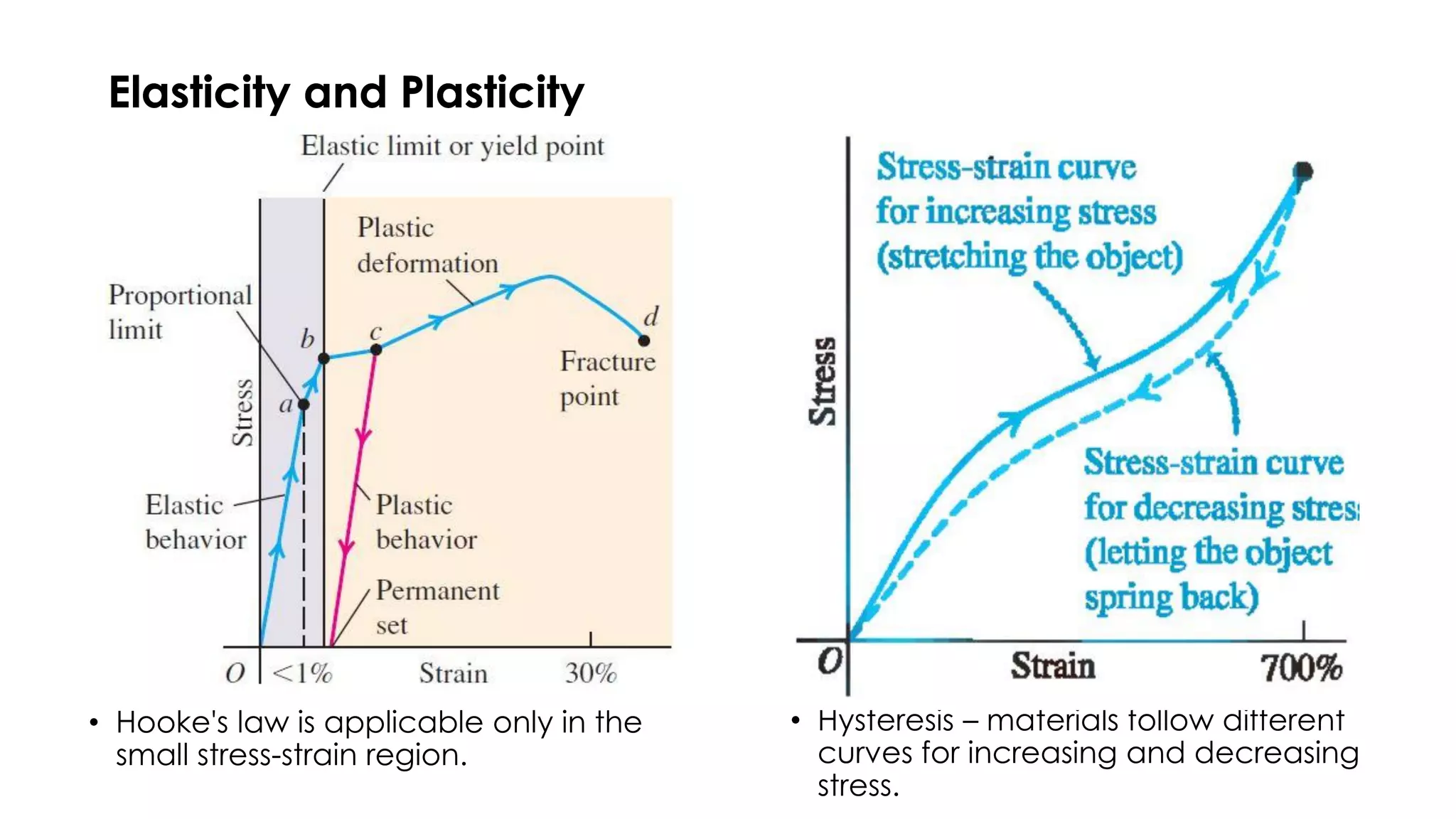
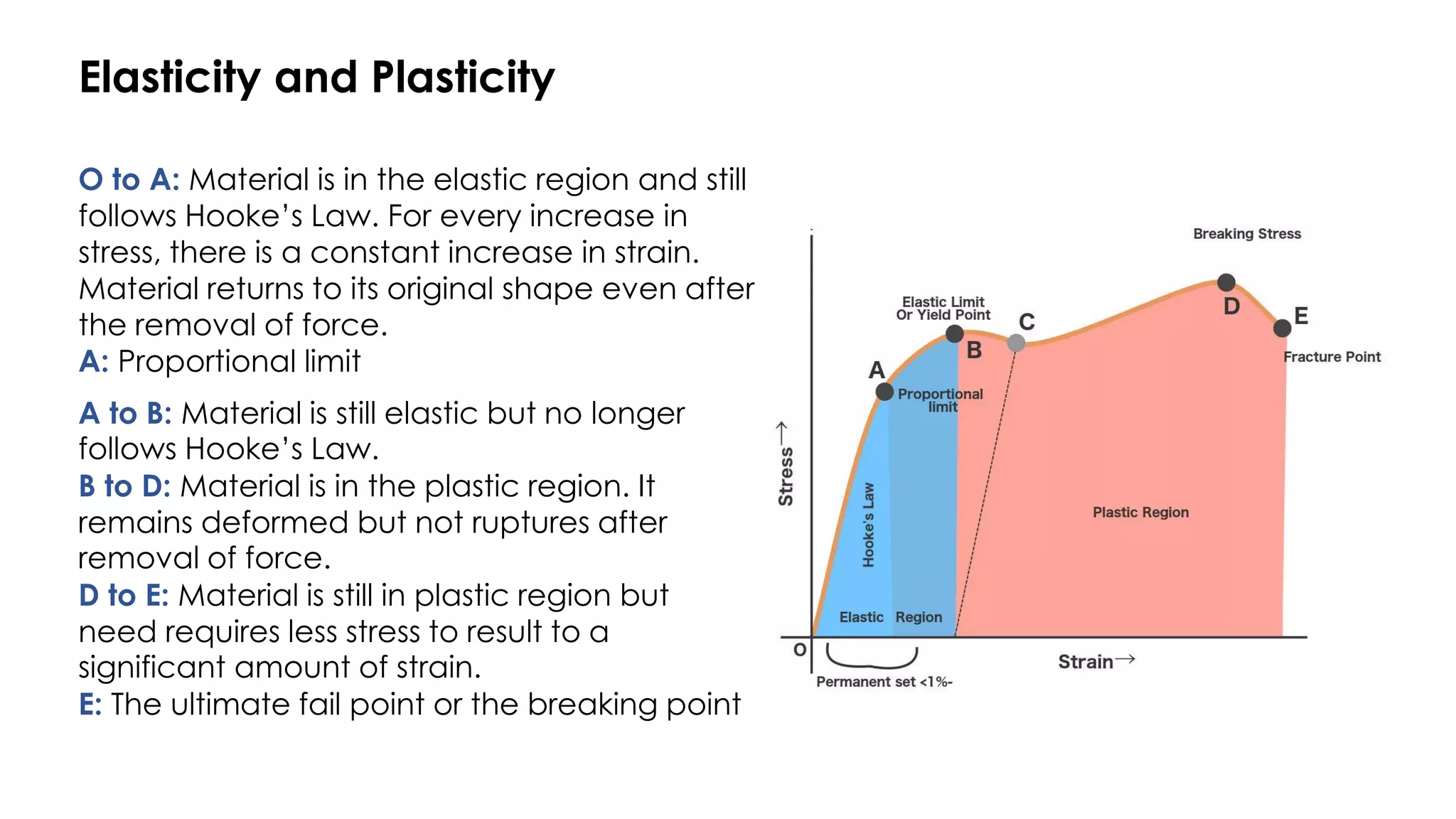
1) Hooke's law states that the ratio of stress to strain is constant, known as the modulus. Stress and strain are directly proportional for small deformations. 2) Young's modulus describes the relationship between tensile stress and tensile strain. Materials with higher Young's modulus are less stretchable. 3) Beyond the proportional limit, materials no longer follow Hooke's law and can enter the plastic region where permanent deformation occurs.

1. Classical Mechanics
Topic 8: Equilibrium and Elasticity
Plasticity
Based from Sears and Zemansky’s University Physics
with Modern Physics 13th ed

2. Stress Strain and Elastic Moduli
● Stress:
– The strength of the forces causing the deformation.
● Strain:
– The resulting deformation.
● Hooke's Law:
– states that the ratio of stress to strain is constant. This ratio is also known
as the MODULUS and it varies depending on the type of strain.
– When the stress and strain are small enough, they are directly
proportional to each other.
𝑆𝑡𝑟𝑒𝑠𝑠
𝑆𝑡𝑟𝑎𝑖𝑛
= 𝐸𝑙𝑎𝑠𝑡𝑖𝑐𝑀𝑜𝑑𝑢𝑙𝑢𝑠

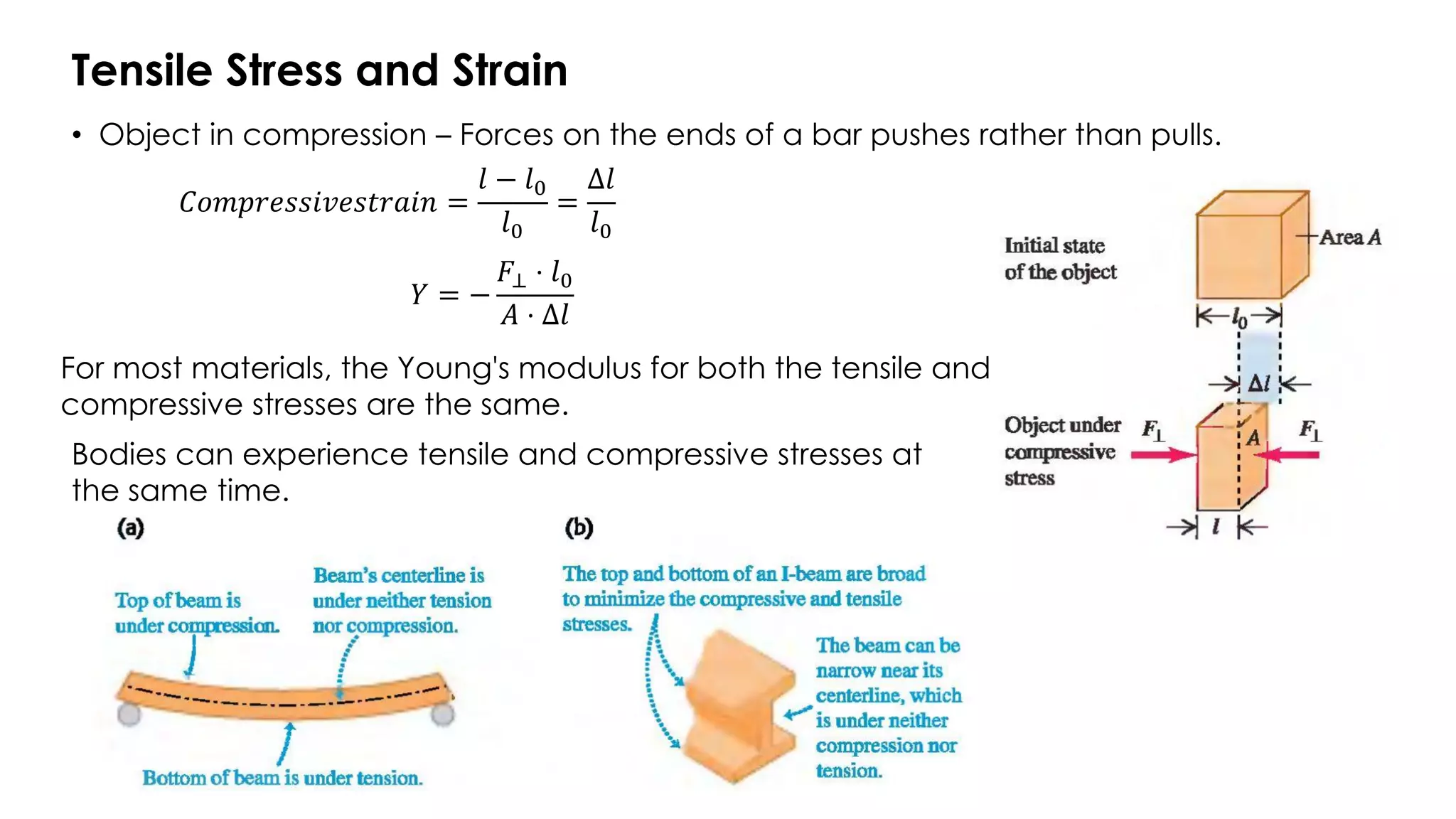
3. Tensile Stress and Strain
• Object in tension – Forces of the same magnitude but opposite in directions are
applied at the object's ends (pulling the object from its ends).
S.I. unit of tensile stress is 1 [N/m2] = 1[Pa]
• Young's modulus (Y)
𝑇𝑒𝑛𝑠𝑖𝑙𝑒 𝑠𝑡𝑟𝑒𝑠𝑠 =
𝐹⊥
𝐴
𝑇𝑒𝑛𝑠𝑖𝑙𝑒 𝑠𝑡𝑟𝑎𝑖𝑛 =
𝑙 − 𝑙0
𝑙0
=
Δ𝑙
𝑙0
𝑌 =
𝑇𝑒𝑛𝑠𝑖𝑙𝑒𝑠𝑡𝑟𝑒𝑠𝑠
𝑇𝑒𝑛𝑠𝑖𝑙𝑒𝑠𝑡𝑟𝑎𝑖𝑛
=
𝐹⊥ ⋅ 𝑙0
𝐴 ⋅ Δ𝑙

4. Tensile Stress and Strain
● A material with higher value of Y
is relatively unstretchable.
Higher stress results to higher strain but
only up to a certain limit called
proportional limit. Beyond this point,
the material no longer follows Hooke’s
Law.

5. Tensile Stress and Strain
• Object in compression – Forces on the ends of a bar pushes rather than pulls.
𝐶𝑜𝑚𝑝𝑟𝑒𝑠𝑠𝑖𝑣𝑒𝑠𝑡𝑟𝑎𝑖𝑛 =
𝑙 − 𝑙0
𝑙0
=
Δ𝑙
𝑙0
𝑌 = −
𝐹⊥ ⋅ 𝑙0
𝐴 ⋅ Δ𝑙
For most materials, the Young's modulus for both the tensile and
compressive stresses are the same.
Bodies can experience tensile and compressive stresses at
the same time.

6. Example:
A cable stretches by an amount d when it supports a crate of mass M. The cable is cut in
half. What is the mass of the load that can be supported by either half of the cable if the
cable stretches by an amount d?
(a) M/4 (b) M/2 (c) M (d) 2M (e) 4M
E3. A cable stretches by an amount d when it supports a crate of mass M. The cable is cut
in half. If the same crate is supported by either half of the cable, by how much will the
cable stretch?
(a) d (b) d/2 (c) d/4 (d) 2d (e) 4d
Tensile Stress and Strain

7. Shear Stress and Strain
• Forces of equal magnitude but opposite direction act tangent to the surfaces of
opposite ends of the object
𝑆ℎ𝑒𝑎𝑟𝑆𝑡𝑟𝑒𝑠𝑠 =
𝐹∥
𝐴
𝑆ℎ𝑒𝑎𝑟𝑆𝑡𝑟𝑎𝑖𝑛 =
𝑥
ℎ
𝑆ℎ𝑒𝑎𝑟𝑀𝑜𝑑𝑢𝑙𝑢𝑠 = 𝑆 =
𝑆ℎ𝑒𝑎𝑟𝑆𝑡𝑟𝑒𝑠𝑠
𝑆ℎ𝑒𝑎𝑟𝑆𝑡𝑟𝑎𝑖𝑛
=
𝐹∥
𝐴
⋅
ℎ
𝑥

8. Elasticity and Plasticity
• Hooke's law is applicable only in the
small stress-strain region.
• Hysteresis – materials follow different
curves for increasing and decreasing
stress.
Elasticity and Plasticity

9. O to A: Material is in the elastic region and still
follows Hooke’s Law. For every increase in
stress, there is a constant increase in strain.
Material returns to its original shape even after
the removal of force.
A: Proportional limit
A to B: Material is still elastic but no longer
follows Hooke’s Law.
B to D: Material is in the plastic region. It
remains deformed but not ruptures after
removal of force.
D to E: Material is still in plastic region but
need requires less stress to result to a
significant amount of strain.
E: The ultimate fail point or the breaking point
Elasticity and Plasticity

10. Bulk Stress and Strain
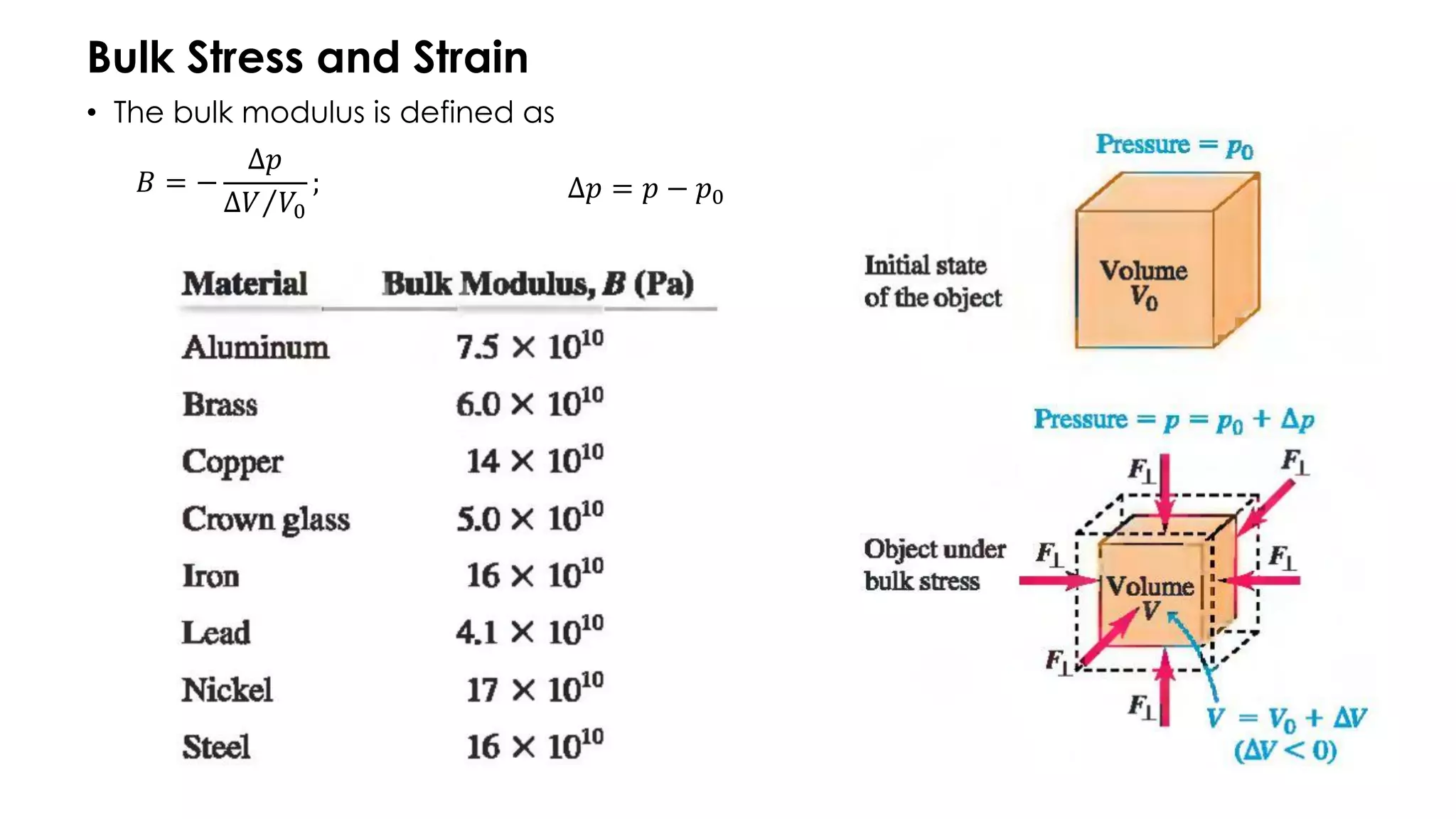
• The stress is now a uniform pressure on all sides, and
the resulting deformation is a volume change.
• S.I. unit of pressure: 1 [N/m2]=1[Pa]
• The force per unit area that the fluid exerts on the
surface of an object immersed object is called the
pressure p:
• The approximate pressure of the earth's atmosphere at
sea level:
• Where V0 is the object's initial volume and ΔV is
the change in volume.
𝑝 =
𝐹⊥
𝐴
1𝑎𝑡𝑚𝑜𝑠𝑝ℎ𝑒𝑟𝑒 = 1 𝑎𝑡𝑚 = 1.013 × 105
𝑃𝑎
𝐵𝑢𝑙𝑘𝑆𝑡𝑟𝑎𝑖𝑛 =
Δ𝑉
𝑉0

11. Bulk Stress and Strain
• The bulk modulus is defined as
𝐵 = −
Δ𝑝
Τ
Δ𝑉 𝑉0
; Δ𝑝 = 𝑝 − 𝑝0