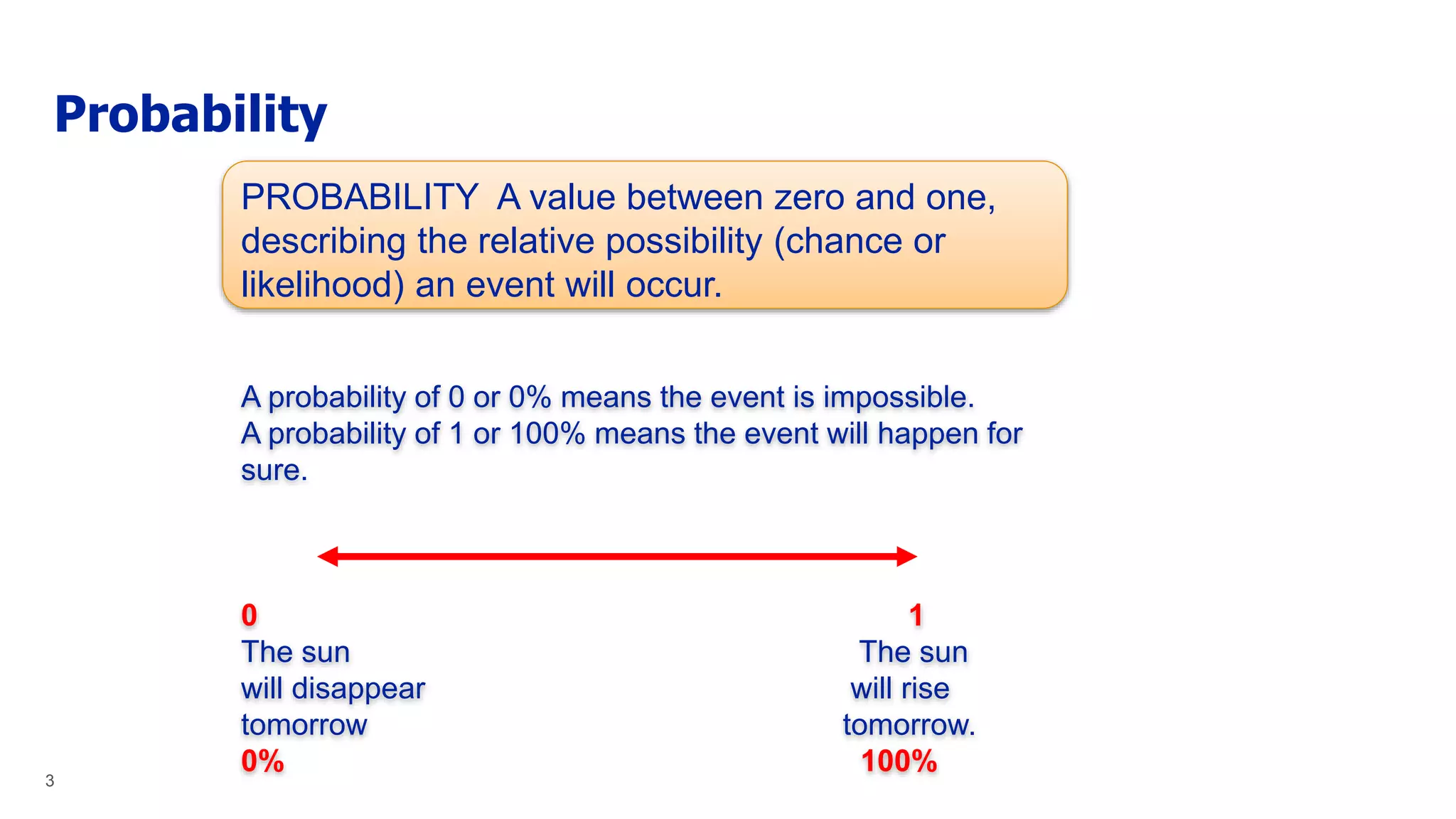
The document explains the addition rules of probability, focusing on mutually exclusive and non-mutually exclusive events. It outlines how to calculate probabilities for both types of events, providing examples relevant to rolling dice and drawing cards. Additionally, it discusses joint probability and includes a practical application involving a survey of tourists visiting two restaurants.

1. CLO 2: Addition Rules of Probability
CIS 2003 Probability and Statistics

2. LEARNING OBJECTIVES
 At the end of this lecture, student should be able to
 Classify events as mutually exclusive and not mutually exclusive
 Apply addition rules of probability to both mutually exclusive and non-
mutually exclusive events.

3. 3
Probability
PROBABILITY A value between zero and one,
describing the relative possibility (chance or
likelihood) an event will occur.
A probability of 0 or 0% means the event is impossible.
A probability of 1 or 100% means the event will happen for
sure.
0 1
The sun The sun
will disappear will rise
tomorrow tomorrow.
0% 100%

4. 4
Addition Rule of Probability : Mutually Exclusive
Events
We can add probabilities as long as the events are mutually exclusive.
Mutually exclusive events cannot happen at the same time - that is, only
one can occur during the experiment.
(If you roll one die, you cannot roll a 6 and a 1. You can roll a 6 or a 1, however).

5. 5
Addition Rules of Probability
There are 2 Addition Rules- for events that are mutually exclusive or are not mutually exclusive.
For Mutually Exclusive Events - If two events A and B are mutually exclusive, the probability of one or the other
event occurring equals the sum of their probabilities.
P(A or B) = P(A) + P(B)
(Remember that events are mutually exclusive if they can’t occur at the same time. )
Example: What is the probability of rolling a number greater than 4 or a number less than
3?
We can call the first event, A (rolling 5 or 6) and the second event, B (rolling 1 or 2).
Since both these events cannot occur at the same time,
P(A) can be added to P(B). i.e. P(A or B) = P(A) + P(B)
=2/6 + 2/6 = 4/6 or 2/3
Question

6. 6
Addition Rules of Probability
For events that are not Mutually Exclusive - If two events A and B are not
mutually exclusive, the probability of one or the other event is given as:
P(A or B) = P(A) + P(B) – P(A and B)
Events are not mutually exclusive if they can occur at the same time.
Example: What is the probability of rolling 4 or more or rolling an odd
number?
Event A: rolling 4 or more ={4,5,6}
Event B: rolling an odd number= {1,3,5}
The outcome 5 is in both events so the events are not mutually
exclusive.
So, P(A or B) = 3/6 + 3/6 – 1/6 =5/6

7. 7
Example 2: What is the probability of rolling a number greater than or
equal to 4 or rolling a 6?
P(4, 5, or 6) + P(6) X We cannot add these because they are not mutually
exclusive. 6 is in both sets so we need another addition rule here!
How would you solve the problem?
Since 6 is already included in the first set, we are still only looking for P(4,5, or 6)
The probability is 3/6 or ½.

8. 8
Picking Cards From a Deck
J Q K A 2 3 4 5 6 7 8 9 10
J Q K A 2 3 4 5 6 7 8 9 10
J Q K A 2 3 4 5 6 7 8 9 10
J Q K A 2 3 4 5 6 7 8 9 10

9. 9
Example 3:What is the probability of picking a 3 or a 10 from a deck of
cards?
(Total 52 cards in a deck).
P(A) = probability of picking a 3.
P(B) = probability of picking a 10.
P(A) = 4/52 because there are 4 threes.
P(B) = 4/52 because there are 4 tens.
P(A or B) = 4/52 + 4/52 = 8/52
= 2/13.

10. 10
Joint Probability
Often events are not mutually exclusive.
Sometimes two or more events can happen at the same time.
This is called joint probability.
For example:
A student can take both English and Mathematics in the same semester.
The probability of a student taking English and Mathematics is an example
of joint probability.

11. 11
Rule of Addition for non-mutually Exclusive Events
If two events are not mutually exclusive the probability of
one or the other occurring (A or B) is calculated by taking
the sum of the individual probabilities minus the joint
probability:
P(A or B) = P(A) + P(B) – P(A and B)

12. 12
Example
What is the probability of rolling a die and observing a number less than or equal to 4,
or a number greater than 3?
P(1,2,3 or 4) or P(4, 5 or 6).
Using a Venn Diagram, 4 is in both events:
1,2 ,3 4 5,6 P(1,2,3 or 4) = 4/6
P(4,5 or 6) = 3/6
P(4) = 1/6
P(1,2,3 or 4) + P(4, 5 or 6) – P(4)
= 4/6 + 3/6 – 1/6 =
= 6/6 = 1 or 100%

13. 13
Picking Cards From a Deck
J Q K A 2 3 4 5 6 7 8 9 10
J Q K A 2 3 4 5 6 7 8 9 10
J Q K A 2 3 4 5 6 7 8 9 10
J Q K A 2 3 4 5 6 7 8 9 10

14. 14
Example 2
What is the probability that a card chosen at random from a standard deck of cards
will be either a king or a heart?
Card Probability
King 4 cards out of 52 4/52
Heart 13 cards out of 52 13/52
P(King or Heart) = P(King) + P(Heart)- P(King and Heart)
P(A or B) = P(A) + P(B) - P(A and B)
= 4/52 + 13/52 - 1/52
= 16/52, or .3077 or 30.77%

15. 15
Example 3
A survey of 1000 tourists to RAK
showed that 800 visited the Pure
Veg Restaurant and 500 visited
the Grand Restaurant. 400
tourists visited both restaurants.
What is the probability that a
selected tourist visited the
Pure Veg Restaurant or the
Grand Restaurant?
P(Pure Veg) + P(Grand) – P(Pure
Veg and Grand)
P(A) + P(B) – P(A and B)
= 800/1000 + 500/1000 -
400/1000
= 900/1000 = 9/10 = 0.9 =
90%
What is the probability that the
selected tourist did not visit
the Pure Veg or the Grand?
1 – 0.9 = 0.1 or 100% -
90% = 10%
What rule did you use to solve
this?
The Complement Rule.
What is the probability that a
tourist visits the Pure Veg and
the Grand Restaurant called?
Joint probability
Are the events of eating at the
Pure Veg and Eating at the
Grand mutually exclusive?
No, because some tourists ate
at both restaurants.

16. 800 MyHCT (800 69428) www.hct.ac.ae