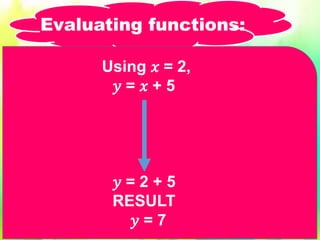
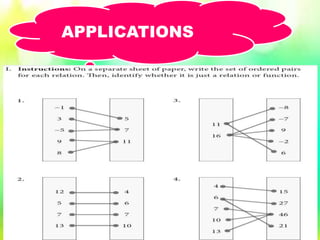
The document outlines learning objectives focused on polynomial functions, evaluation of functions, and the relationships between different groups of entities. It explains concepts of relations and functions, including one-to-one and many-to-one relationships, illustrated with examples of family dynamics. Additionally, it provides evaluations and exercises for specific equations, emphasizing the process of substituting values to find corresponding outputs.

2. Learning Objectives:
1. Illustrates polynomial functions.
2. Evaluates functions.
3. Express satisfaction in mastery
of new ways of thinking through
application of mathematics.

3. GAMES

5. MOTHER

7. FATHER

9. GRANDPARENTS

11. SIBLINGS

12. Questions:
1.When do we say that
people are related?
2. What qualifies for two
people to have a relation?

13. Partners :
(Milagros, Ernesto) (Teresa, Rudy) (Maureen, Jun)
First Second First Second First Second
Group Group Group Group Group Group

14. Relations and functions:
 Relations are made up of two groups, both with at least
one object in them that are connected by some
characteristic or rule.
 Use arrows to show connections between pairs of
objects between groups.
 Emphasize that in writing ordered pairs, the elements
must be written in a strict order: (first group, second
group).
 All functions are relations, but not all relations are
functions.
RELATION - A set of one or more
ordered pairs

15. have all elements in the first group
paired with exactly one object in the
second group (one-to-one relation). If an
element in the second group is paired
with two or more objects in the first
group, it can still be a function provided
that the first statement is still followed
(many-to-one relation).
FUNCTIONS

16. Partners :
NANAY TATAY
MILAGROS ERNESTO
TERESA RUDY
MAUREEN JUN

17. This is an example of a
function because each
person has exactly one
partner. Moreover, this
illustration shows a one-to-
one function because for
every one nanay, there
corresponds only one tatay
from the second group.

18. CHILDREN FATHER
Diane
Manny
Marianne
Joseph
Lando
Kenneth
Children-to-parent

19. In addition, this illustration
shows a many-to-one function
because there are more than
one child that has one tatay.
For instance, Diane and
Marianne connect to Manny as
their tatay. Similarly, Joseph
and Kenneth connect to Tatay
Lando.

20. One-to-many and many-to-
many relations cannot be
functions and are simply
referred to as RELATIONS.

21. LOLA GRANDCHILDREN
Jose
Lola Tinay
Basyang
Pedro
Mutya
Grandparent to Grandchildren

22. This illustration shows a one-
to-many correspondence
because Lola Basyang
connects to more than one
grandchildren (Jose, Tinay,
Pedro, and Mutya).

23. • Recall equations in two
variables 𝑥 and 𝑦. Give some
simple examples of these
equations such as:
𝑦 = 𝑥 + 1 𝑦 = 𝑥 + 3 𝑦 = 𝑥 − 5
Evaluating functions:

24. • Recall substitution of a value in x to
get the value of 𝒚.
Using 𝑥 = 1,
𝑦 = 𝑥 + 5
𝑦 = 1 + 5
RESULT
𝑦 = 6
Evaluating functions:

25. Using 𝑥 = 2,
𝑦 = 𝑥 + 5
𝑦 = 2 + 5
RESULT
𝑦 = 7
Evaluating functions:

26. Using 𝑥 = 3,
𝑦 = 𝑥 + 5
𝑦 = 3 + 5
RESULT
𝑦 = 8
Evaluating functions:

27. Explain that equations are also
relations of numbers relating 𝒙
and 𝒚.

28. INPUT EQUATION OUTPUT
(x) (x + 5) (y)
1 1 + 5 6
2 2 + 5 7
3 3 + 5 8
Imagine that we are processing the numbers, as shown below, by
substituting each value in place of x:
1 + 5
2 + 5
3 + 5

31. APPLICATIONS

32. II. Instructions: Determine the value of y by
replacing x in each equation with the given
value.
1. y = 8x - 10 x = 6
2. y = −3x + 5 x = −1
3. y = 15 − 8x x = 4
4. y = 2 + 7x x = 1
5. y = -9x − 100 x = −10
APPLICATIONS

33. APPLICATIONS

34. Maraming Salamat!