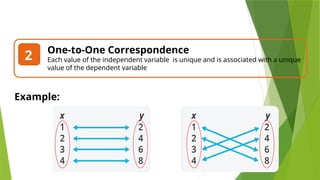
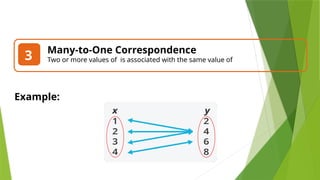
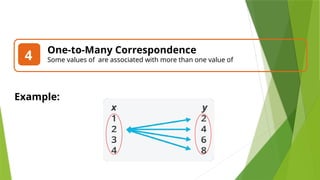
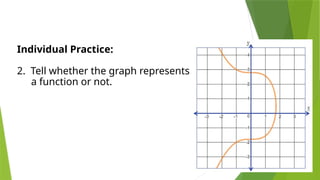
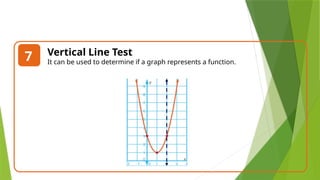
This lesson aims to teach the distinction between functions and relations, with clear definitions and examples. It covers types of correspondence, the vertical line test for identifying functions, and provides individual and group exercises for practice. The lesson emphasizes understanding the different ways to represent functions and their applications in real life.

1. Lesson 2
Functions vs.
Relations

2. At the end of this lesson, the learner should be able to
 clearly define relations and functions;
 correctly differentiate a function from a relation; and
 accurately determine whether a given scenario is a
function or not.

3.  What is a relation?
 How will you distinguish a function from a relation?

4. In this lesson, you will learn how to distinguish functions
from relations. One way to do that is by observing their
graphs!
Let’s take a look at this short video to have some background
about the different types of relations.
LegaC. “Correspondence between Variables.” Youtube (June
2016). Retrieved 20 February 2019 from
https://www.youtube.com/watch?v=em_KshLsCxU

5. ● In the video, what are the two types of test used to
determine the correspondence between variables?
● Among the types of correspondence, which of them
represents a function? Why do you say so?

6. Relation
a set of objects, such as numbers, grouped with one another which may or may
not represent a pattern; simply a set of ordered pairs that are arranged in an
orderly manner
1
Example:
Billy is associated to his friends: Gabriel, Jasmine, and Luis.
We can define a relation showing Billy’s association or
correspondence.

7. One-to-One Correspondence
Each value of the independent variable is unique and is associated with a unique
value of the dependent variable
2
Example:

8. Many-to-One Correspondence
Two or more values of is associated with the same value of
3
Example:

9. One-to-Many Correspondence
Some values of are associated with more than one value of
4
Example:

10. Many-to-Many Correspondence
Some values of and are associated with more than one value of their
counterpart
5
Example:

11. Function
It is a special kind of relation in which no two distinct ordered pairs have the
same first element.
6
Example:
Miguel, Karlo, and Bien are paired to their respective schools.
Let us name this relation .
is a function because no two ordered pairs have the same
first element.

12. Vertical Line Test
It can be used to determine if a graph represents a function.
7
Example:
The given graph on the right passes the
vertical line test since if we draw an
imaginary vertical line anywhere on the
graph, it would touch exactly one point.

13. Example 1: Determine whether the following set is a
function.

14. Answer:
No first element was repeated.
Hence, the set of ordered pairs represents a function.
Example 1: Determine whether the following set is a
function.

15. Example 1: Write all the ordered pairs in the
figure and determine the type of
relation depicted by the given
figure.

16. Example 1: Write all the ordered pairs in the
figure and determine the type of
relation depicted by the given
figure.
Solution:
Pairing each element of with each element of , we have
Observe that more than one element in set are
associated with the same element in set . Thus, the
figure shows a many-to-one type of relation.

17. Individual Practice:
1. Determine whether the following table of values satisfies
the definition of a function.
0 1 4 16
0

18. Individual Practice:
2. Tell whether the graph represents
a function or not.

19. Group Practice: To be done by 2-5 groups
Given:
a. Complete the table of values.
b. Sketch the graph of .
c. Determine whether is a function of .
0 2

20. Relation
a set of objects, such as numbers, grouped with one another which may or may
not represent a pattern; simply a set of ordered pairs that are arranged in an
orderly manner
1
One-to-One Correspondence
Each value of the independent variable is unique and is associated with a unique
value of the dependent variable
2
Many-to-One Correspondence
Two or more values of is associated with the same value of
3

21. One-to-Many Correspondence
Some values of are associated with more than one value of
4
Many-to-Many Correspondence
Some values of and are associated with more than one value of their
counterpart
5
Function
It is a special kind of relation in which no two distinct ordered pairs have the
same first element.
6

22. Vertical Line Test
It can be used to determine if a graph represents a function.
7

23. ● What is the difference between a function and a relation?
● Why is it important to know that there are a lot of ways to
represent a function?
● How do we make use of functions to solve real-life
problems?