This document is a lecture on trigonometric functions from Dr. Pranav Sharma of the Maths Learning Centre in Jalandhar. It derives trigonometric identities for the sum and difference of angles, including formulas for cos(θ + φ), cos(θ - φ), and relationships between trig functions of complementary angles like cos(π/2 - x) = sin(x). Diagrams and algebraic steps are shown to demonstrate the derivations.

![youtube.com/@MathematicsOnlineLectures
TRIGONOMETRIC FUNCTIONS OF SUM AND DIFFERENCE OF NUMBERS
(i) 𝐜𝐨𝐬 (𝜽 + 𝝋) = 𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋 − 𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 𝝋
(ii) 𝐜𝐨𝐬 (𝜽 − 𝝋) = 𝐜𝐨𝐬 𝟔 𝐜𝐨𝐬 𝝋 + 𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 𝝋
Let 𝐗′
𝑶𝐗 and 𝐘𝑶𝐘′
be the coordinate axes. With 𝑶 as the centre and taking a unit
radius, draw a circle, cutting the axes at 𝑨, 𝑨′
, 𝑩 and 𝑩′
as shown in the figure.
Let ∠𝑨𝑶𝑷 = 𝜽 and ∠𝑷𝑶𝑸 = 𝝋. Then,
∠𝑨𝑶𝑸 = (𝜽 + 𝝋) .
Let ∠𝑨𝑶𝑹 = −𝝋. Join 𝑷𝑹 and 𝑨𝑸.
(i) The points on the circle are given by
𝑷( 𝐜𝐨𝐬 𝜽, 𝐬𝐢𝐧 𝜽), 𝑸[ 𝐜𝐨𝐬 (𝜽 + 𝝋),
𝐬𝐢𝐧 (𝜽 + 𝝋)], 𝑹[ 𝐜𝐨𝐬 (−𝝋), 𝐬𝐢𝐧 (−𝝋)],
i.e., 𝑹( 𝐜𝐨𝐬 𝝋, − 𝐬𝐢𝐧 𝝋), 𝑨(𝟏, 𝟎), 𝑩(𝟎, 𝟏),
𝑨′(−𝟏, 𝟎) and 𝑩′(𝟎, 𝟏) .
In △ 𝑷𝑶𝑹 and △ 𝑸𝑶𝑨, we have 𝑷𝑶 =
𝑸𝑶 = 𝟏 unit, 𝑶𝑹 = 𝑶𝑨 = 𝟏 unit and
∠𝑷𝑶𝑹 = ∠𝑸𝑶𝑨 [each equal to (𝝋 + ∠𝑸𝑶𝑹)]. So, △ 𝑷𝑶𝑹 ≅△ 𝑸𝑶𝑨.
Hence, 𝑷𝑹 = 𝑸𝑨.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture3-230616085353-4897c830/85/Class-11_Chapter-3_Lecture_3-2-320.jpg)
![youtube.com/@MathematicsOnlineLectures
Therefor, 𝑷𝑹𝟐
= 𝑸𝑨𝟐
⇒ ( 𝐜𝐨𝐬 𝜽 − 𝐜𝐨𝐬 𝝋)𝟐
+ ( 𝐬𝐢𝐧 𝜽 + 𝐬𝐢𝐧 𝝋)𝟐
= [ 𝐜𝐨𝐬 (𝜽 + 𝝋) − 𝟏]𝟐
+ [ 𝐬𝐢𝐧 (𝜽 + 𝝋) − 𝟎]𝟐
⇒ (𝒄𝒐𝒔𝟐
𝜽 + 𝐜𝐨𝐬𝟐
𝝋 − 𝟐 𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋) +(𝐬𝐢𝐧𝟐
𝜽 + 𝐬𝐢𝐧𝟐
𝝋 + 𝟐 𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 𝝋)
= [𝐜𝐨𝐬𝟐(𝜽 + 𝝋) + 𝟏 − 𝟐 𝐜𝐨𝐬 (𝜽 + 𝝋)] + 𝐬𝐢𝐧𝟐(𝜽 + 𝝋)
⇒ (𝒄𝒐𝒔𝟐
𝜽 + 𝐬𝐢𝐧𝟐
𝜽) +(𝐜𝐨𝐬𝟐
𝝋 + 𝐬𝐢𝐧𝟐
𝝋) − 𝟐( 𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋 − 𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 𝝋)
= [𝐜𝐨𝐬𝟐(𝜽 + 𝝋) + 𝐬𝐢𝐧𝟐(𝜽 + 𝝋)] + 𝟏 − 𝟐 𝐜𝐨𝐬 (𝜽 + 𝝋)
⇒ 𝟐 − 𝟐( 𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋 − 𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 𝝋) = 𝟐 − 𝟐 𝐜𝐨𝐬 (𝜽 + 𝝋)
⇒ ( 𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋 − 𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 𝝋) = 𝐜𝐨𝐬 (𝜽 + 𝝋) .
Hence, 𝐜𝐨𝐬 (𝜽 + 𝝋) = 𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋 − 𝐬𝐢𝐧 𝜽𝐬i𝐧𝝋.
(ii) (1) Replacing 𝝋𝐛𝐲 − 𝝋 in identity (1), we get
𝐜𝐨𝐬 (𝜽 − 𝝋) = 𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 (−𝝋) − 𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 (−𝝋) .
Hence, 𝐜𝐨𝐬 (𝜽 − 𝝋) = 𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋 + 𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 𝝋
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture3-230616085353-4897c830/85/Class-11_Chapter-3_Lecture_3-3-320.jpg)
![youtube.com/@MathematicsOnlineLectures
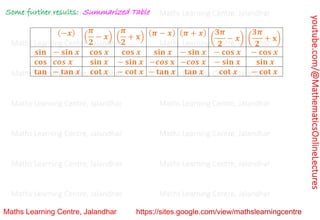
(i) 𝐜𝐨𝐬 (
𝝅
𝟐
− 𝒙) = 𝐬𝐢𝐧 𝒙 (ii) 𝒔𝒊𝒏 (
𝝅
𝟐
− 𝒙) = 𝐜𝐨𝐬 𝒙
(iii) 𝐭𝐚𝐧 (
𝝅
𝟐
− 𝒙) = 𝐜𝐨𝐭 𝒙 (iv) 𝐜𝐨𝐭 (
𝝅
𝟐
− 𝒙) = 𝐭𝐚𝐧 𝒙
(v) 𝐬𝐞𝐜 (
𝝅
𝟐
− 𝒙) = 𝐜𝐨𝐬𝐞𝐜 𝒙 (vi) 𝐜𝐨𝐬𝐞𝐜 (
𝝅
𝟐
− 𝒙) = 𝐬𝐞𝐜 𝒙
(i) 𝐜𝐨𝐬 (
𝝅
𝟐
− 𝒙) = 𝐜𝐨𝐬
𝝅
𝟐
𝐜𝐨𝐬 𝒙 + 𝐬𝐢𝐧
𝝅
𝟐
𝐬𝐢𝐧 𝒙 = 𝐬𝐢𝐧 𝒙.
(ii) 𝐬𝐢𝐧 (
𝝅
𝟐
− 𝒙) = 𝐬𝐢𝐧 𝜽, where 𝜽 = (
𝝅
𝟐
− 𝒙)
= 𝐜𝐨𝐬 (
𝝅
𝟐
− 𝜽) = 𝐜𝐨𝐬 {
𝝅
𝟐
− (
𝝅
𝟐
− 𝒙)} = 𝐜𝐨𝐬 𝒙.
(iii) 𝐭𝐚𝐧 (
𝝅
𝟐
− 𝒙) =
𝐬𝐢𝐧 (
𝝅
𝟐
−𝒙)
𝐜𝐨𝐬 (
𝝅
𝟐
−𝒙)
=
𝐜𝐨𝐬 𝒙
𝐬𝒊𝒏 𝒙
= 𝐜𝐨𝐭 𝒙 [using (ii) and (i)].
(iv) 𝐜𝐨𝐭 (
𝝅
𝟐
− 𝒙) =
𝐜𝐨𝐬 (
𝝅
𝟐
−𝒙)
𝐬𝐢𝐧 (
𝝅
𝟐
−𝒙)
=
𝐬𝒊𝒏 𝒙
𝐜𝐨𝐬 𝒙
= 𝐭𝐚𝐧 𝒙 [using (i) and (ii)].
(v) 𝐬𝐞𝐜 (
𝝅
𝟐
− 𝒙) =
𝟏
𝐜𝐨𝐬 (
𝝅
𝟐
−𝒙)
=
𝟏
𝐬𝐢𝐧 𝒙
= 𝐜𝐨𝐬𝐞𝐜 𝒙 = 𝐜𝐨𝐬𝐞𝐜 𝒙.
(vi) 𝐜𝐨𝐬𝐞𝐜 (
𝝅
𝟐
− 𝒙) =
𝟏
𝐬𝐢𝐧 (
𝝅
𝟐
−𝒙)
=
𝟏
𝐜𝐨𝐬 𝒙
= 𝐬𝐞𝐜 𝒙.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture3-230616085353-4897c830/85/Class-11_Chapter-3_Lecture_3-4-320.jpg)
![youtube.com/@MathematicsOnlineLectures
(i) 𝐜𝐨𝐬 (
𝝅
𝟐
+ 𝒙) = − 𝐬𝐢𝐧 𝒙 (ii) 𝐬𝐢𝐧 (
𝝅
𝟐
+ 𝒙) = 𝐜𝐨𝐬 𝒙
(iii) 𝐭𝐚𝐧 (
𝝅
𝟐
+ 𝒙) = − 𝐜𝐨𝐭 𝒙 (iv) 𝐜𝐨𝐭 (
𝝅
𝟐
+ 𝒙) = − 𝐭𝐚𝐧 𝒙
(v) 𝐬𝐞𝐜 (
𝝅
𝟐
+ 𝒙) = − 𝐜𝐨𝐬𝐞𝐜 𝒙 (vi) 𝐜𝐨𝐬𝐞𝐜 (
𝝅
𝟐
+ 𝒙) = 𝐬𝐞𝐜 𝒙
(i) 𝐜𝐨𝐬 (
𝝅
𝟐
+ 𝒙) = 𝐜𝐨𝐬
𝝅
𝟐
𝐜𝐨𝐬 𝒙 − 𝐬𝐢𝐧
𝝅
𝟐
𝐬𝐢𝐧 𝒙 = −𝐬𝒊𝒏 𝒙.
(ii) 𝐬𝐢𝐧 (
𝝅
𝟐
+ 𝒙) = 𝐬𝐢𝐧 [
𝝅
𝟐
− (−𝒙)] = 𝐜𝐨𝐬 (−𝒙) [ 𝐬𝐢𝐧 (
𝝅
𝟐
− 𝜽) = 𝐜𝐨𝐬 𝜽] = 𝐜𝐨𝐬 𝒙
(iii) 𝐭𝐚𝐧 (
𝝅
𝟐
+ 𝒙) =
𝐬𝐢𝐧 (
𝝅
𝟐
+𝒙)
𝐜𝐨𝐬 (
𝝅
𝟐
+𝒙)
=
𝒄𝒐𝒔 𝒙
−𝒔𝒊𝒏 𝒙
= − 𝐜𝐨𝐭 𝒙.
(iv) 𝐜𝐨𝐭 (
𝝅
𝟐
+ 𝒙) =
𝟏
𝐭𝐚𝐧 (
𝝅
𝟐
+𝒙)
=
𝟏
− 𝐜𝐨𝐭 𝒙
= − 𝐭𝐚𝐧 𝒙.
(v) 𝐬𝐞𝐜 (
𝝅
𝟐
+ 𝒙) =
𝟏
𝐜𝐨𝐬 (
𝝅
𝟐
+𝒙)
=
𝐥
− 𝐬𝐢𝐧 𝒙
= − 𝐜𝐨𝐬𝐞𝐜 𝒙.
(vi) 𝐜𝐨𝐬𝐞𝐜 (
𝝅
𝟐
+ 𝒙) =
𝟏
𝐬𝐢𝐧 (
𝝅
𝟐
+𝒙)
=
𝟏
𝐜𝐨𝐬 𝒙
= 𝐬𝐞𝐜 𝒙.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture3-230616085353-4897c830/85/Class-11_Chapter-3_Lecture_3-5-320.jpg)
![youtube.com/@MathematicsOnlineLectures
(i) 𝐜𝐨𝐬 (𝝅 − 𝒙) = − 𝐜𝐨𝐬 𝒙 (ii) 𝐬𝐢𝐧 (𝝅 − 𝒙) = 𝐬𝐢𝐧 𝒙
(iii) 𝐭𝐚𝐧 (𝝅 − 𝒙) = − 𝐭𝐚𝐧 𝒙 (iv) 𝐜𝐨𝐭 (𝝅 − 𝒙) = − 𝐜𝐨𝐭 𝒙
(v) 𝐬𝐞𝐜 (𝝅 − 𝒙) = − 𝐬𝐞𝐜 (vi) 𝐜𝐨𝐬𝐞𝐜 (𝝅 − 𝒙) = 𝐜𝐨𝐬𝐞𝐜 𝒙
𝐜𝐨𝐬 (𝝅 − 𝒙) = 𝐜𝐨𝐬 𝝅 𝐜𝐨𝐬 𝒙 + 𝐬𝐢𝐧 𝝅 𝐬𝐢𝐧 𝒙 = − 𝐜𝐨𝐬 𝒙.
𝐬𝐢𝐧 (𝝅 − 𝒙) = 𝐬𝐢𝐧 [
𝝅
𝟐
+ (
𝝅
𝟐
− 𝒙)] = 𝐜𝐨𝐬 (
𝝅
𝟐
− 𝒙) = 𝐬𝒊𝐧𝒙
𝐭𝐚𝐧 (𝝅 − 𝒙) =
𝐬𝐢𝐧 (𝝅 − 𝒙)
𝐜𝐨𝐬 (𝝅 − 𝒙)
=
𝐬𝒊𝒏 𝒙
− 𝐜𝐨𝐬 𝒙
= − 𝐭𝐚𝐧 𝒙.
𝐜𝐨𝐭 (𝝅 − 𝒙) =
𝟏
𝐭𝐚𝐧 (𝝅−𝒙)
=
𝐥
− 𝐭𝐚𝐧 𝒙
= − 𝐜𝐨𝐭 𝒙.
𝐬𝐞𝐜 (𝝅 − 𝒙) =
𝟏
𝐜𝐨𝐬 (𝝅−𝒙)
=
𝟏
− 𝐜𝐨𝐬 𝒙
= − 𝐬𝐞𝐜 𝒙.
𝐜𝐨𝐬𝐞𝐜 (𝝅 − 𝒙) =
𝟏
𝐬𝐢𝐧 (𝝅−𝒙)
=
𝟏
𝐬𝐢𝐧 𝒙
= 𝐜𝐨𝐬𝐞𝐜 𝒙.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture3-230616085353-4897c830/85/Class-11_Chapter-3_Lecture_3-6-320.jpg)
![youtube.com/@MathematicsOnlineLectures
(i) 𝐜𝐨𝐬 (𝝅 + 𝒙) = − 𝐜𝐨𝐬 𝒙 (ii) 𝐬𝒊𝐧(𝝅 + 𝒙) = − 𝐬𝐢𝐧 𝒙
(iii) 𝐭𝐚𝐧 (𝝅 + 𝒙) = 𝐭𝐚𝐧 𝒙 (iv) 𝐜𝐨𝐭 (𝝅 + 𝒙) = 𝐜𝐨𝐭 𝒙
(v) 𝐬𝐞𝐜 (𝝅 + 𝒙) = − 𝐬𝐞𝐜 𝒙 (vi) 𝐜𝐨𝐬𝐞𝐜 (𝝅 + 𝒙) = − 𝐜𝐨𝐬𝐞𝐜 𝒙
(i) 𝐜𝐨𝐬 (𝝅 + 𝒙) = 𝐜𝐨𝐬 𝝅 𝐜𝐨𝐬 𝒙 − 𝐬𝐢𝐧 𝝅 𝐬𝐢𝐧 𝒙 = − 𝐜𝐨𝐬 𝒙.
(ii) 𝐬𝐢𝐧 (𝝅 + 𝒙) = 𝐬𝐢𝐧 [
𝝅
𝟐
+ (
𝝅
𝟐
+ 𝒙)] = 𝐜𝐨𝐬 (
𝝅
𝟐
+ 𝒙) = −𝐬𝒊𝒏 𝒙.
(iii) 𝐭𝐚𝐧 (𝝅 + 𝒙) =
𝐬𝐢𝐧 (𝝅+𝒙)
𝐜𝐨𝐬 (𝝅+𝒙)
=
− 𝐬𝐢𝐧 𝒙
− 𝐜𝐨𝐬 𝒙
= 𝐭𝐚𝐧 𝒙.
(iv) 𝐜𝐨𝐭 (𝝅 + 𝒙) =
𝟏
𝐭𝐚𝐧 (𝝅+𝒙)
=
𝟏
𝐭𝐚𝐧 𝒙
= 𝐜𝐨𝐭 𝒙.
(v) 𝐬𝐞𝐜 (𝝅 + 𝒙) =
𝟏
𝐜𝐨𝐬 (𝝅+𝒙)
=
𝟏
− 𝐜𝐨𝐬 𝒙
= − 𝐬𝐞𝐜 𝒙.
(vi) 𝐜𝐨𝐬𝐞𝐜 (𝝅 + 𝒙) =
𝟏
𝐬𝐢𝐧 (𝝅+𝒙)
=
𝐥
− 𝐬𝐢𝐧 𝒙
= − 𝐜𝐨𝐬𝐞𝐜 𝒙.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture3-230616085353-4897c830/85/Class-11_Chapter-3_Lecture_3-7-320.jpg)
![youtube.com/@MathematicsOnlineLectures
(i) 𝐬𝐢𝐧 (𝜽 + 𝝋) = 𝐬𝐢𝐧 𝜽 𝐜𝐨𝐬 𝝋 + 𝐜𝐨𝐬 𝜽 𝐬𝐢𝐧 𝝋
(ii) 𝐬𝐢𝐧 (𝜽 − 𝝋) = 𝐬𝐢𝐧 𝜽 𝐜𝐨𝐬 𝝋 − 𝐜𝐨𝐬 𝜽 𝐬𝐢𝐧 𝝋
(i) 𝐬𝐢𝐧 (𝜽 + 𝝋) = 𝐜𝐨𝐬 [
𝝅
𝟐
− (𝜽 + 𝝋)] = 𝐜𝐨𝐬 [(
𝝅
𝟐
− 𝜽) − 𝝋]
= 𝐜𝐨𝐬 (
𝝅
𝟐
− 𝜽) 𝐜𝐨𝐬 𝝋 + 𝐬𝐢𝐧 (
𝝅
𝟐
− 𝜽) 𝐬𝐢𝐧 𝝋
= 𝐬𝐢𝐧 𝜽 𝐜𝐨𝐬 𝝋 + 𝐜𝐨𝐬 𝟔 𝐬𝐢𝐧 𝝋.
Hence, 𝐬𝐢𝐧 (𝜽 + 𝝋) = 𝐬𝐢𝐧 𝜽 𝐜𝐨𝐬 𝝋 + 𝐜𝐨𝐬 𝜽 𝐬𝐢𝐧 𝝋.
(ii) Replacing 𝝋 by −𝝋 in (i), we get
𝐬𝐢𝐧 [𝜽 + (−𝝋)] = 𝐬𝐢𝐧 𝜽 𝐜𝐨𝐬 (−𝝋) + 𝐜𝐨𝐬 𝜽 𝐬𝐢𝐧 (−𝝋)
⇒ 𝐬𝐢𝐧 (𝜽 − 𝝋) = 𝐬𝐢𝐧 𝜽 𝐜𝐨𝐬 𝝋 − 𝐜𝐨𝐬 𝜽 𝐬𝐢𝐧 𝝋
[ 𝐜𝐨𝐬 (−𝝋) = 𝐜𝐨𝐬 𝝋, 𝐬𝐢𝐧 (−𝝋) = − 𝐬𝐢𝐧 𝝋].
Hence, 𝐬𝐢𝐧 (𝜽 − 𝝋) = 𝐬𝐦
̇ 𝜽 𝐜𝐨𝐬 𝝋 − 𝒄𝒐𝒔𝜽 𝐬𝐢𝐧 𝝋.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture3-230616085353-4897c830/85/Class-11_Chapter-3_Lecture_3-9-320.jpg)
![youtube.com/@MathematicsOnlineLectures
If none of the angles 𝜽, 𝝋 and (𝜽 + 𝝋) is an odd multiple of 𝝅/𝟐 then
(𝒊) 𝐭𝐚𝐧 (𝜽 + 𝝋) =
𝐭𝐚𝐧 𝜽+ 𝐭𝐚𝐧 𝝋
𝟏− 𝐭𝐚𝐧 𝜽 𝐭𝐚𝐧 𝝋
(ii) 𝐭𝐚𝐧 (𝜽 − 𝝋) =
𝐭𝐚𝐧 𝜽− 𝐭𝐚𝐧 𝝋
𝟏+ 𝐭𝐚𝐧 𝜽 𝐭𝐚𝐧 𝝋
(i) 𝐭𝐚𝐧 (𝜽 + 𝝋) =
𝐬𝐢𝐧 (𝜽+𝝋)
𝐜𝐨𝐬 (𝜽+𝝋)
=
( 𝐬𝐢𝐧 𝜽 𝐜𝐨𝐬 𝝋+ 𝐜𝐨𝐬 𝜽 𝐬𝐢𝐧 𝝋)
( 𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋−𝐬𝐦
̇ 𝜽 𝐬𝐢𝐧 𝝋)
=
(
𝐬𝐢𝐧 𝜽 𝐜𝐨𝐬 𝝋
𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋
+
𝐜𝐨𝐬 𝜽 𝐬𝐢𝐧 𝝋
𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋
)
(
𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋
𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋
−
𝐬𝐢𝐧 𝜽𝐬𝐦
̇ 𝝋
𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋
)
[dividing 𝐧𝐮𝐦. and denom. by 𝒄𝒐𝒔𝜽 𝐜𝐨𝐬 𝝋]
=
𝐭𝐚𝐧 𝜽 + 𝐭𝐚𝐧 𝝋
𝟏 − 𝐭𝐚𝐧 𝜽 𝐭𝐚𝐧 𝝋
.
Hence, 𝐭𝐚𝐧 (𝜽 + 𝝋) =
𝐭𝐚𝐧 𝜽+ 𝐭𝐚𝐧 𝝋
𝟏− 𝐭𝐚𝐧 𝜽 𝐭𝐚𝐧 𝝋
.
(ii) Replacing 𝝋𝐛𝐲 − 𝝋 in (i), we get
𝐭𝐚𝐧 [𝜽 + (−𝝋)] =
𝐭𝐚𝐧 𝜽 + 𝐭𝐚𝐧 (−𝝋)
𝟏 − 𝐭𝐚𝐧 𝜽 𝐭𝐚𝐧 (−𝝋)
⇒ 𝐭𝐚𝐧 (𝜽 − 𝝋) =
𝐭𝐚𝐧 𝜽 − 𝐭𝐚𝐧 𝝋
𝟏 + 𝐭𝐚𝐧 𝜽 𝐭𝐚𝐧 𝝋
.
Hence, 𝐭𝐚𝐧 (𝜽 − 𝝋) =
𝐭𝐚𝐧 𝜽− 𝐭𝐚𝐧 𝝋
𝟏+ 𝐭𝐚𝐧 𝜽 𝐭𝐚𝐧 𝝋
.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture3-230616085353-4897c830/85/Class-11_Chapter-3_Lecture_3-10-320.jpg)
![youtube.com/@MathematicsOnlineLectures
If none of the angles 𝜽, 𝝋 and (𝜽 + 𝝋) is a multiple of 𝝅 then
(i) 𝐜𝐨𝐭 (𝜽 + 𝝋) =
𝐜𝐨𝐭 𝜽 𝐜𝐨𝐭 𝝋−𝟏
𝐜𝐨𝐭 𝝋+ 𝐜𝐨𝐭 𝜽
(ii) 𝐜𝐨𝐭 (𝜽 − 𝝋) =
𝐜𝐨𝐭 𝜽 𝐜𝐨𝐭 𝝋+𝟏
𝐜𝐨𝐭 𝝋− 𝐜𝐨𝐭 𝜽
(i) 𝐜𝐨𝐭 (𝜽 + 𝝋) =
𝐜𝐨𝐬 (𝜽+𝝋)
𝐬𝐢𝐧 (𝜽+𝝋)
=
( 𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋− 𝐬𝐢𝐧 𝜽𝐬𝐦
̇ 𝝋)
( 𝐬𝐢𝐧 𝜽 𝐜𝐨𝐬 𝝋+ 𝐜𝐨𝐬 𝜽 𝐬𝐢𝐧 𝝋)
=
(
𝐜𝐨𝐬 𝜽 𝐜𝐨𝐬 𝝋
𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 𝝋
−
𝐬𝐦
̇ 𝜽 𝐬𝐢𝐧 𝝋
𝐬𝐦
̇ 𝜽 𝐬𝐢𝐧 𝝋
)
(
𝐬𝐢𝐧 𝜽 𝐜𝐨𝐬 𝝋
𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 𝝋
+
𝐜𝐨𝐬 𝜽 𝐬𝐢𝐧 𝝋
𝐬𝐢𝐧 𝜽𝐬𝐦
̇ 𝝋
)
[dividing 𝐧𝐮𝐦. and denom. by 𝐬𝐢𝐧 𝜽 𝐬𝐢𝐧 𝝋]
=
𝐜𝐨𝐭 𝜽 𝐜𝐨𝐭 𝝋 − 𝟏
𝐜𝐨𝐭 𝝋 + 𝐜𝐨𝐭 𝜽
.
Hence, 𝐜𝐨𝐭 (𝜽 + 𝝋) =
𝐜𝐨𝐭 𝜽 𝐜𝐨𝐭 𝝋−𝟏
𝐜𝐨𝐭 𝝋+ 𝐜𝐨𝐭 𝜽
.
(ii) Replacing 𝝋𝐛𝐲 − 𝝋 in (i), we get
𝐜𝐨𝐭 [𝜽 + (−𝝋)] =
𝐜𝐨𝐭 𝜽 𝐜𝐨𝐭 (−𝝋) − 𝟏
𝐜𝐨𝐭 (−𝝋) + 𝐜𝐨𝐭 𝜽
⇒ 𝐜𝐨𝐭 (𝜽 − 𝝋) =
− 𝐜𝐨𝐭 𝜽 𝐜𝐨𝐭 𝝋 − 𝟏
− 𝐜𝐨𝐭 𝝋 + 𝐜𝐨𝐭 𝜽
⇒ 𝐜𝐨𝐭 (𝜽 − 𝝋) =
𝐜𝐨𝐭 𝜽 𝐜𝐨𝐭 𝝋+𝟏
𝐜𝐨𝐭 𝝋− 𝐜𝐨𝐭 𝜽
. Hence, 𝐜𝐨𝐭 (𝜽 − 𝝋) =
𝐜𝐨𝐭 𝜽 𝐜𝐨𝐭 𝝋+𝟏
𝐜𝐨𝐭 𝝋− 𝐜𝐨𝐭 𝜽
.
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar
Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar Maths Learning Centre, Jalandhar](https://image.slidesharecdn.com/class11chapter3lecture3-230616085353-4897c830/85/Class-11_Chapter-3_Lecture_3-11-320.jpg)
