Chessboard Puzzles Part 2 - Independence

Chessboard Puzzles: Independence
Part 2 of a 4-part Series of Papers on the Mathematics of the Chessboard
by Dan Freeman
May 1, 2014

Dan Freeman Chessboard Puzzles: Independence
MAT 9000 Graduate Math Seminar
Table of Contents
Table of Figures .............................................................................................................................. 3
Introduction ..................................................................................................................................... 4
Definition of Independence............................................................................................................. 4
Rooks Independence ....................................................................................................................... 5
Bishops Independence..................................................................................................................... 7
Kings Independence ...................................................................................................................... 10
Knights Independence................................................................................................................... 12
The 8-queens Problem .................................................................................................................. 14
Proof that β(Qnxn) = n .................................................................................................................... 17
The n-queens Problem .................................................................................................................. 21
Conclusion .................................................................................................................................... 23
Sources Cited ................................................................................................................................ 25
2

Table of Figures
Image 1: Rook Movement............................................................................................................... 5
Image 2: Eight Independent Rooks on 8x8 Board .......................................................................... 6
Image 3: All Six Permutations of Three Independent Rooks on 3x3 Boards ................................. 7
Image 4: Bishop Movement ............................................................................................................ 7
Image 5: Maximum Set of Independent Bishops on 8x8 Board ..................................................... 8
Image 6: Pairs of Independent Bishops on Either the Top and Bottom Rows
or the Left and Right Columns...................................................................................................... 10
Image 7: King Movement ............................................................................................................. 10
Image 8: Maximum Set of Independent Kings on 8x8 Board ...................................................... 11
Image 9: Maximum Set of Independent Kings on 9x9 Board ...................................................... 12
Image 10: Knight Movement ........................................................................................................ 13
Image 11: Queen Movement......................................................................................................... 14
Image 12: The 1 5 8 6 3 7 2 4 Solution to the 8-queens Problem................................................. 15
Image 13: The 4 2 8 5 7 1 3 6 Solution to the 8-queens Problem................................................. 17
Image 14: Ten Independent Queens on 10x10 Board................................................................... 18
Image 15: Eight Independent Queens on 8x8 Board Using Cloning Construction ...................... 19
Image 16: Nine Independent Queens on 9x9 Board Using Clone Construction .......................... 21
Image 17: Doubly Centrosymmetric Solution to the 5-queens Problem ...................................... 22
Table 1: Independence Number Notation ....................................................................................... 4
Table 2: Sum of Row and Column Numbers for the 1 5 8 6 3 7 2 4 Solution.............................. 15
Table 3: Sum of Row and Column Numbers for the 1 5 8 6 3 7 2 4 Solution.............................. 15
Table 4: Permutations of Solutions to the 8-queens Problem ....................................................... 16
Table 5: Solutions to the n-queens Problem by Symmetry Type for 4 ≤ n ≤ 15 .......................... 23
Table 6: Domination Number Formulas by Piece ........................................................................ 23
Table 7: Independence Number Formulas by Piece ..................................................................... 24
3

Introduction
4
This paper analyzes the concept of chessboard independence, a similar but different idea
from domination, which was examined in my first paper on chessboard puzzles. Like
domination, independence is a problem that involves placing an optimal amount of chess pieces
of a particular type on a chessboard. However, unlike domination, which is a minimization
problem, independence is a maximization problem. Therefore, the way to attack puzzles with
independence differs somewhat from the approach used in domination. In addition, the level of
knowledge and understanding regarding formulas and patterns associated with independence will
naturally deviate from what is known about domination.
In a structure that closely parallels my first paper in this series, this paper seeks to
provide a full survey of chessboard independence among rooks, bishops, kings, knights and
queens. In doing this, I hope to be able to make the link between the two ideas of domination
and independence by comparing and contrasting what has already been established vs. what
remains as an open problem.
Definition of Independence
An independent set of chess pieces is one such that no piece in the set attacks another
piece in the set. The independence number for a certain piece and certain size mxn1chessboard is
the maximum number of independent pieces that can be placed on the board; a set of such
maximum size is called a maximum independent set [1, p. 163]. Independence numbers are
denoted by β(Pmxn) where P represents the type of chess piece, as denoted in Table 1.
Table 1: Independence Number Notation
Piece Abbreviation
Knight N
Bishop B
Rook R
Queen Q
King K
1 Throughout this paper, m and n refer to arbitrary positive integers denoting the number of rows and columns of a
chessboard, respectively.

5
Note that the domination number γ(Pmxn) ≤ β(Pmxn) for all pieces P and for all m and n.
To see why this is the case, suppose that a maximum independent set of pieces, call it I, fails to
dominate a chessboard. In other words, there exists at least one square on the board that is not
covered by any piece in I and hence γ(Pmxn) > β(Pmxn). Then one could simply add as many
independent pieces as are required on the uncovered squares so as to dominate the entire board.
But then this dominating set of pieces, call it D, would be an independent set larger than I,
contradicting the fact that I is a maximum independent set. Therefore, the number of pieces in a
maximum independent set I must be at least as many as the number of pieces in a minimum
dominating set D. Put more concisely, γ(Pmxn) ≤ β(Pmxn) [1, p. 164].
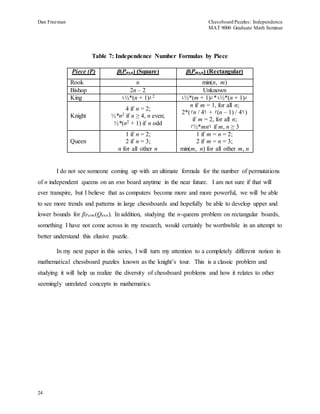
Rooks Independence
Recall from my first paper on chessboard domination that rooks are permitted to move
any number of squares either horizontally or vertically, as long as they do not take the place of a
friendly piece or pass through any piece (own or opponent’s) currently on the board. In Image
1, the white rook can move to any of the squares with a white circle and the black rook can move
to any of the squares with a black circle [4].
Image 1: Rook Movement
As with domination, independence among rooks is the simplest of all chess pieces and
β(Rnxn) = n. The proof for this formula is quite simple. There are n rows and n columns on an
nxn board. In order to be independent, no two rooks may lie on the same column or same row.
Therefore, an independent set of rooks may contain no more than n rooks. Furthermore, n rooks
placed along the main diagonal is an independent set since no two rooks share the same row or

the same column. As a result, we have that β(Rnxn) ≤ n and β(Rnxn) ≥ n, which implies that
β(Rnxn) = n. This result is illustrated in Image 2.
6
Image 2: Eight Independent
Rooks on 8x8 Board
Also in line with rooks domination is the fact that for a general rectangular mxn
chessboard, β(Rmxn) = min(m, n). The argument that is this case closely parallels that for the
square chessboard. Without loss of generality, suppose that m < n. Clearly, if there are more
than m rooks on the board, then there exists a pair of rooks that lie on the same row. Therefore,
β(Rmxn) ≤ m. Also, if m rooks are placed in a diagonal fashion on the board, then this set of rooks
is independent and β(Rmxn) ≥ m. Since we have designated m as the lesser of m and n, we have
that β(Rmxn) = m = min(m, n). A symmetric argument works if we suppose that m > n so the
proof is complete.
A formula for the number of permutations of maximum independent sets of rooks on an
nxn square board is also well-known. The number of such permutation is n!,[1, p. 179] and we
shall denote this number by βPerm(Rnxn), where the subscripted “Perm” is a shorthand indication
for the number of permutations. As with the proof for the rooks independence number, the proof
that βPerm(Rnxn) = n! is straightforward. A rook may be placed on any of the n squares of the first
column. Another rook may be placed on any of the n – 1 squares in the second column not in the
same row as the rook in the first column. Yet another rook may be placed on any of the n – 2
squares in the third column not in the same row as either of the rooks in the first two columns.
This process continues until the nth and final column is reached when just 1 square will remain
for the final rook. Therefore, the number of permutations is n*(n – 1)*(n – 2) * … *3*2*1 = n!.

The six different permutations of sets of three independent rooks on a 3x3 board are shown in
Image 3 [1, p. 179].
Bishops Independence
7
Image 3: All Six Permutations of Three
Independent Rooks on 3x3 Boards
Recall that bishops move diagonally any number of squares as long as they do not take
the place of a friendly piece or pass through any piece (own or opponent’s) currently on the
board. In Image 4, the white bishop can move to any of the squares with a white circle and the
black bishop can move to any of the squares with a black circle [4].
Image 4: Bishop Movement
The formula for the bishops independence number differs from the formula for the
bishops domination number. While γ(Bnxn) = n, β(Bnxn) = 2n – 2. The proof is fairly
straightforward. For any nxn chessboard, there are 2n – 1 positive diagonals (as well as 2n – 1

negative diagonals2). Except for opposite corner squares, exactly one bishop may be placed in
each diagonal so as to have an independent set of bishops. In the case of opposing corner
squares, only one bishop may be placed on one of the two squares, in order to avoid two bishops
attacking each other from corner to corner. Therefore, the number of pieces in an independent
set of bishops must be no more than one fewer than the number of diagonals, or (2n – 1) – 1 = 2n
– 2. Additionally, one may place n – 1 bishops along the top row and n – 1 bishops along the
bottom row, as in Image 5, for a total of 2n – 2 bishops that are independent. Therefore, β(Bnxn)
= 2n – 2 [1, p. 182].
8
Image 5: Maximum Set of
Independent Bishops on 8x8 Board
As might be expected, as is the case with the bishops domination number, no formula is
currently known for the bishops independence number on a general rectangular board [2, p. 13].
In 1964, the Yaglom brothers proved that a maximum set of independent bishops must be
placed on the outermost edges of the board. That is, either half of the 2n – 2 bishops must be
placed on the top row and half on the bottom row, or the bishops need to be placed half and half
on the left and right edges. To begin, assume that 2n – 2 independent bishops have been placed
on the board. Label each square with the number of bishops that cover it. A square cannot be
controlled by more than two bishops as this would result in at least one pair of bishops that attack
each other. Also, a square cannot be controlled by zero bishops, since then the set of
2 Hereafter within the Bishops Independence section of this paper, the sign (positive or negative) associated with
diagonals will be omitted, as this is not an important distinction.

independent bishops would not be maximum. Therefore, each square gets assigned a label of 1
or 2 [1, p. 183].
9
Now we will show that at least 2n squares on the board are labeled with a 1. The four
corner squares can only be controlled by a single bishop, whether the squares are occupied or
not. At least two of the corner squares must be unoccupied in order to have an independent set
of bishops. In addition, the 2n – 2 squares containing bishops clearly have a label of 1.
Together, the 2 unoccupied corner squares and the 2n – 2 squares containing bishops each having
a label of 1 result in there being at least (2n – 2) + 2 = 2n squares with a label of 1 [1, pp. 183-
184].
Next, let S be the sum of the labels for the entire chessboard. Since there are at least 2n
squares with a label of 1, the remaining n2 – 2n squares have a label of 1 or 2. This results in the
following inequality: S ≤ 1*(2n) + 2*(n2 – 2n) = 2n2 – 2n = n*(2n – 2). Now we seek to obtain a
lower bound for S. A bishop on the outer ring of edge squares (top, bottom, left or right edges)
covers exactly n squares. A bishop inside of the outermost ring controls at least n + 2 squares
(this number increases by 2 for each move the bishop makes closer to the center of the board).
Let a be the number of bishops in the interior of the board and b be the number of bishops on the
outermost ring. So, by construction, a + b = 2n – 2 and we have the following inequality: S ≥
b*n + a*(n+2) = n*(a + b) + 2a = n*(2n – 2) + 2a. All together, we now have S bounded below
and above, as follows: n*(2n – 2) + 2a ≤ S ≤ n*(2n – 2), which implies that n*(2n – 2) + 2a ≤
n*(2n – 2). The only way this latter inequality can possibly hold is if a = 0. In other words,
there cannot be any bishops on the interior of the board, and so all of them must be on the
outermost ring [1, p. 184].
Now that we have proved that all bishops in a maximum independent set must be placed
on the outer ring of edge squares, we are well-equipped to go about proving a formula for the
number of permutations of 2n – 2 independent bishops on an nxn square chessboard. There are
2n such arrangements. Because a bishop must be on an edge square, we need only consider the
possible arrangements of bishops on the top row. First consider the squares on the four corners
of the board. A bishop may be placed on one of two opposite corners. Since there are two pairs
of opposite corners, there are 2*2 = 4 permutations of independent bishops on the corner squares.
Next we turn our attention to the non-corner squares. For any non-corner square in the top row,

either that square in the top row and the square straight down from it in the bottom row contain
bishops while the two squares on the left and right edge diagonally from the top and bottom
squares are unoccupied or the top and bottom squares are left open and the squares on the left
and right edges contain bishops. These facts are illustrated in Image 6. So for each of the n – 2
columns not on the left or right edges of the board, there are two possible arrangements of
independent bishops. Combined with the fact that are two permutations for each of the columns
on the left and right edges, we conclude that βPerm(Bnxn) = 22*2n – 2 = 2n [1, pp. 184-185].
Kings Independence
10
Image 6: Pairs of Independent Bishops on Either the
Top and Bottom Rows or the Left and Right Columns
Recall that kings are allowed to move exactly one square in any direction as long as they
do not take the place of a friendly piece. In Image 7, the king can move to any of the squares
with a white circle [4].
Image 7: King Movement

11
As with the kings domination number, a formula has been established for the kings
independence number. The formula, β(Knxn) = └½*(n + 1)┘
2, is different from the kings
domination number formula (recall that that γ(Knxn) = └(n + 2) / 3┘
2) but similar in that both
formulas involve the floor function and a term that gets squared. The proof is relatively
straightforward [1, p. 185].
First, note that any 2x2 square on a chessboard may contain at most one independent
king. When n is even, the board can be split into (½*n)2 squares and so β(Knxn) = (½*n)2 [1, pp.
185-186]. The case when n is even is illustrated on an 8x8 board in Image 8.
Independent Kings on 8x8 Board
Now if n is odd, one can divide the board into (½*(n – 1)2 2x2 squares, ½*(n – 1) 1x2
rectangles, ½*(n – 1) 2x1 rectangles and one 1x1 square. Each of these areas may contain at
most one independent king, so β(Knxn) = (½*(n – 1)2 + 2*(½*(n – 1)) + 1 = (½*(n + 1)2. The
formulas for n even and n odd can be condensed into a single formula using the floor function3,
as follows: β(Knxn) = └½*(n + 1)┘
2. Since n is odd, the king in the 1x1 square fixes the
arrangement of all the other kings on the board; hence such a maximum arrangement of
independent kings is unique [1, p. 186]. The case when n is odd is shown on a 9x9 board in
Image 9.
3 Throughout this paper, the symbols ‘└’ and ‘┘’ will be used to indicate the greatest integer or floor function.

12
Independent Kings on 9x9 Board
Furthermore, like we were able to do with the kings domination number formula, we can
generalize kings independence to rectangular boards by expanding the squared term in the
formula into two separate factors and replacing the n variable with an m variable in one of them,
as follows: β(Kmxn) = └½*(m + 1)┘*└½*(n + 1)┘.
Knights Independence
Recall that knights move two squares in one direction (either horizontally or vertically)
and one square in the other direction as long as they don’t take the place of a friendly piece. In
Image 10, the white and black knights can move to squares with circles of the corresponding
color [4].

13
Image 10: Knight Movement
Unlike with knights domination, a formula is known for the knights independence
number. The formula is broken into three separate cases, as follows [1, p. 181]:
4 if n = 2
β(N
nxn
) = ½*n2 if n ≥ 4, n even
½*(n2 + 1) if n odd
I will omit the proof of the above formula since it relies on a concept known as the
knight’s tour that we won’t explore until the third paper in this series. I will be sure to revisit
this proof at the appropriate point in that paper.
For the sake of completeness, it should be mentioned that a somewhat more complicated
formula (which we will not prove in this or any subsequent paper) is known for the knights
independence number on a general mxn rectangular board. The formula, which makes use of the
ceiling function4, is as follows [5]:
n if m = 1
β(N
m xn
) = 2*(┌n / 4┐ + ┌(n – 1) / 4┐) if m = 2
┌½*mn┐ if m, n ≥ 3
4 Throughout this paper, the symbols ‘┌’ and ‘┐’ will be used to indicate the least integer or ceiling function.

The 8-queens Problem
14
Recall that queens move horizontally, vertically and diagonally any number of squares as
long as they do not take the place of a friendly piece or pass through any piece (own or
opponent’s) currently on the board. In Image 11, the queen can move to any of the squares with
a black circle [4].
Image 11: Queen Movement
A classic chessboard puzzle is the 8-queens problem, in which one attempts to place 8
independent queens on an 8x8 chessboard. The problem was first presented by a chess player
named Max Bezzel in a German newspaper in September 1948. Less than two years later, in
June 1850, Franz Nauck posed the problem in another German newspaper. Nauck correctly
published all 92 solutions to the 8-queens problem in the same paper on September 21, 1850.
During that same summer, Carl Friedrich Gauss read Nauck’s account of the problem and began
studying it on his own [1, pp. 164-165].
In all his brilliance, Gauss used permutations of the numbers 1 through 8 to analyze
solutions to the 8-queens problem. For example, the permutation 1 5 8 6 3 7 2 4 corresponds to a
solution to the 8-queens problem (shown in Image 12) in which the queen in the first column
from the left is placed in the first row from the bottom, the queen in the second column from the
left is placed in the fifth row from the bottom, and so on. Gauss devised a method for
determining whether an arrangement of 8 queens on an 8x8 board is independent. For each
queen, if the sum of its row number and column number (again, from bottom to top, from left to
right) is unique to this sum for all other queens, then it follows that no two queens lie on the
same negative diagonal. Additionally, for each queen, if the sum of its row number and reverse
column number (from bottom to top, from right to left) is distinct from that of all other queens,

then it follows that no two queens lie on the same positive diagonal. If these two conditions
hold, then the 8 queens are independent [1, pp. 165-166].
15
Image 12: The 1 5 8 6 3 7 2 4
Solution to the 8-queens Problem
In the aforementioned 1 5 8 6 3 7 2 4 permutation of 8 queens, the sums of the row
numbers and column numbers and the sums of the row numbers and reverse column numbers for
each queen are shown in Tables 2 and 3, respectively.
Table 2: Sum of Row and Column Numbers for the 1 5 8 6 3 7 2 4 Solution
Row # 1 5 8 6 3 7 2 4
Column # 1 2 3 4 5 6 7 8
Sum 2 7 11 10 8 13 9 12
Table 3: Sum of Row and Column Numbers for the 1 5 8 6 3 7 2 4 Solution
Row # 1 5 8 6 3 7 2 4
Reverse
8 7 6 5 4 3 2 1
Column #
Sum 9 12 14 11 7 10 4 5
In his 1953 book Mathematical Recreations, Maurice Kraitchik provided all 92 solutions
to the 8-queens problem. There are 11 permutations which account for 8 different arrangements
when all rotations and reflections are considered and one additional permutation which is

symmetric under rotations of 180° and hence gives rise to 4 different solutions. These 12
different permutations are shown in Table 4 [1, pp. 166-167].
16
Table 4: Permutations of Solutions to the 8-queens Problem
Permutation No. of Solutions
1 5 8 6 3 7 2 4 8
1 6 8 3 7 4 2 5 8
2 4 6 8 3 1 7 5 8
2 5 7 1 3 8 6 4 8
2 5 7 4 1 8 6 3 8
2 6 1 7 4 8 3 5 8
2 6 8 3 1 4 7 5 8
2 7 3 6 8 5 1 4 8
2 7 5 8 1 4 6 3 8
3 5 8 4 1 7 2 6 8
3 6 2 5 8 1 7 4 8
3 5 2 8 1 7 4 6 4
As an additional note on the 8-queens problem, H.E. Dudeney observed that all but one
of the 12 fundamental solutions consists of three queens lying on a straight line (though
obviously not along the same row, column or diagonal, for then the set of queens would not be
independent). For instance, in the 1 5 8 6 3 7 2 4 solution shown in Image 12, the queens on
squares (2, 5), (4, 6) and (6, 7) lie on a straight line, where the coordinates (x, y) correspond to
the xth column from the left and the yth row from the bottom5. One solution to the 8-queens
problem that does not exhibit three queens in a straight line is 4 2 8 5 7 1 3 6, shown in Image 13
[1, pp. 167-168].
5Throughout this paper, this (x, y) coordinate notation will be used.

Proof that β(Qnxn) = n
17
Image 13: The 4 2 8 5 7 1 3 6
Solution to the 8-queens Problem
Before we extend the 8-queens problem to a more general n-queens problem, it would be
prudent to first examine the queens independence number for square nxn boards. In stark
contrast to queens domination, the queens independence number has a known formula and a very
simple one too: β(Q2x2) = 1, β(Q3x3) = 2 and for n ≠ 2 or 3, β(Qnxn) = n. The proof, however, is
not nearly as simple and requires considering a number of different cases.
First, let’s get the easy cases where 1 ≤ n ≤ 3 out of the way. The n = 1 case is
completely trivial, as we can only place a single queen on the lone square of the board; hence
β(Q1x1) = 1. The n = 2 case is almost as trivial, as we note that if two or more queens are placed
on a 2x2 board, then they will necessarily be adjacent to each other; so β(Q2x2) = 1. When n = 3,
note that each queen placed along the edge of the board (that is, any square other than the center
square) will control exactly 7 of the 9 squares on the board. The two squares not under attack
will lie on the same row, column or diagonal. Thus, no more than 2 independent queens can be
placed on a 3x3 board and β(Q2x2) = 3.
For n ≥ 4, we will have to split the proof up into even and odd cases and further divide
the even case into two subcases, one which n ≡ 2 mod 6 and the other in which n ≢ 2 mod 6.
Let’s first consider the subcase where n ≢ 2 mod 6. We start by placing a queen on the (1, 2)

square and make repeated knight’s moves, one square and two squares up, until you hit the top
row. At this point, we have placed ½*n queens on the board that control all of the columns on
the left half of the board and all of the even-numbered rows. Now we place a queen in the
bottom row, one column over from where we left off, and continue the same placement of
queens until we reach the right edge of the board. These ½*n queens on the right side of the
board control all of the columns on the right half of the board, as well as all of the odd-numbered
rows. We have now placed n independent queens on an nxn board where n ≢ 2 mod 6; this is
shown for n = 10 in Image 14 [1, pp. 170-171].
18
Image 14: Ten Independent Queens
on 10x10 Board
Now the only thing we need to worry about in the case where n ≢ 2 mod 6 is whether or
not any of the queens on the left half of the board lie on the same negative diagonal as any of the
queens on the right half of the board. Let n = 2k. The rth queen on the left side of the board is
on square (r, 2r) and the sum of these two coordinates is 3r. The sth queen on the right side of
the board is at (k + s, 2s – 1). If these two queens occupy the same negative diagonal, then (k +
s) + (2s – 1) = 3r, that is, 3s + k – 1 = 3r. If we substitute k with ½*n and isolate n, the equation
becomes n = 6*(r – s) + 2. This implies that if two queens are on the same negative diagonal,
then n ≡ 2 mod 6. Therefore, our construction above works precisely for even n where n ≢ 2
mod 6 [1, pp. 171].

19
Now for n = 8, 14, 20, …, that is n ≡ 2 mod 6, we start by placing a queen at (2, 3) and
then doing repeated knight’s moves, as we did before, until we reach the second row from the
top. At this point, the leftmost column and the bottom row are uncovered. In order to account
for these uncovered squares, we revert to the second-to-last knight we placed (the one on the
fourth row from the top), and “clone” it into two copies. We move one copy straight over to the
leftmost column and the other straight down to the bottom row. Letting n = 2k, we now have
placed k queens that control all of the columns in the left half of the board as well as all of the
odd-numbered rows. In order to take care of the right half of the board, rotate the board 180°
and repeat the same knight’s move construction. This construction on an 8x8 board is illustrated
in Image 15, in which the squares on which the “cloned” queens originated are shaded in gray
with arrows pointing to the final destinations of the cloned queens [1, pp. 172-173].
Image 15: Eight Independent
Queens on 8x8 Board Using
Cloning Construction
In order to verify that this construction works for all n ≡ 2 mod 6, imagine that the
cloning steps described above were skipped. That is, the cloned queens in the left column and
the bottom row were removed from the board and the queen from where they came was placed
back on the board. Likewise, the cloned queens in the right column and the top row disappear
and the queen from where they originated reappears. In order to confirm that these remaining n
– 2 queens are independent, we need only check that no queen from the left half of the board
occupies the same negative diagonal as a queen from the right half of the board. The rth queen
on the left side of the board occupies square (r + 1, 2r + 1) while the sth queen on the right side

of the board occupies square (k + s, 2s). If two queens lie on the same negative diagonal, then (r
+ 1) + (2r + 1) = (k + s) + (2s), that is, 3r + 2 = 3s + k. Since n = 2k, this equation resolves to n =
6*(r – s) + 4, which implies that n ≡ 4 mod 6, contradicting the fact that n ≡ 2 mod 6. Therefore,
these n – 2 queens are independent [1, pp. 172-173].
20
The only piece that remains to show is that the introduction of the cloned queens does not
compromise the independence of the n queens. It suffices to check that the cloned queens do not
lie on the same negative diagonal as one of the other queens on the board. The clone on the left
edge is situated at (1, n – 3) and the rth queen on the left side of the board is located at (r + 1, 2r
+ 1). So if these two queens lie on the same negative diagonal, then (1) + (n – 3) = (r + 1) + (2r
+ 1), which simplifies to n – 2 = 3r + 2. Therefore, n = 3r + 4 ≡ 1 mod 3, contradicting the fact n
≡ 2 mod 6. If the cloned queen at (1, n – 3) lies on the same diagonal as an sth queen on the right
side of the board, then n – 2 = (k + s) + (2s) = 3s + k. Since n = 2k, we have that n – 2 = 3s +
½*n, which implies that n = 6s + 4 ≡ 4 mod 6, another contradiction. Now the cloned queen on
the bottom row is at square (k – 1, 1), and if this queen lies on the same negative diagonal as the
rth queen on the left half of the board, then (k – 1) + (1) = (r + 1) + (2r + 1). This simplifies to k
= 3r + 2, or equivalently n = 6r + 4, which, again, contradicts the fact that n ≡ 2 mod 6. Also, if
this cloned queen lies on the same negative diagonal as the sth queen on the right half of the
board, then k = 3s + k, which implies that s = 0, which is nonsense, since s is a positive integer.
This fact makes intuitive sense since the queen is at the bottom of the board on the left side and
so cannot possibly share a negative diagonal with any queen on the right side of the board.
Lastly, a symmetric argument works for the cloned queen on the right side of the board and the
one on the top row [1, pp. 173-174].
Now the proof that β(Qnxn) = n for all even n ≥ 4 is complete. This makes the proof for
odd-sized boards is easy. The construction we used for even boards, whether n ≡ 2 mod 6 or not,
leaves the main positive diagonal unoccupied. Therefore, for any even n, we simply add a row to
the top and a column to the right of the board and place a queen in the upper-right hand corner to
produce a set of n + 1 independent queens on this new (n + 1)x(n + 1) board. Image 16 shows
this construction for a 9x9 board, with the additional row and column shaded in orange. This
completes the longwinded proof [1, p. 174].

21
Image 16: Nine Independent
Queens on 9x9 Board Using
Clone Construction
As a bonus, it has been shown that β(Qmxn) = min(m, n) for any mxn rectangular board
with the exception of the aforementioned 2x2 and 3x3 cases [3, p. 9].
The n-queens Problem
Now we turn our attention to the n-queens problem, that is, how many different ways can
one place n independent queens on an nxn board? While we have a value for β(Qnxn) for all
values of n, the n-queens problem itself remains far from solved. In Mathematical Recreations,
Maurice Kraitchik provides the number of solutions of arrangements of n independent queens for
small values of n and classifies these solutions based on their level of symmetry, as follows [1,
pp. 174-175]:
 Ordinary solutions (O): solutions with no symmetry and thus yield a total of 8
solutions under rotation and reflection
 Centrosymmetric solutions (C): solutions that are unchanged under rotations of
180° but are changed by other rotations or reflections and thus yield a total of 4
solutions

22
 Doubly Centrosymmetric solutions (Q): solutions that are unchanged under any
rotation but are changed by reflections and yield a total of 2 solutions
An example of an ordinary solution to the n-queens problem is the 1 5 8 6 3 7 2 4
solution to the 8-queens problem in Image 12. A centrosymmetric solution is the 5 3 1 7 2 8 6 4
solution in which we used the cloning construction in Image 15. Finally, the 2 5 3 1 4 solution
to the 5-queens problem is doubly centrosymmetric and is shown in Image 17 [1, pp. 175].
Image 17: Doubly
Centrosymmetric Solution
to the 5-queens Problem
Kraitchik identified the number of solutions to the n-queens problem by symmetry type
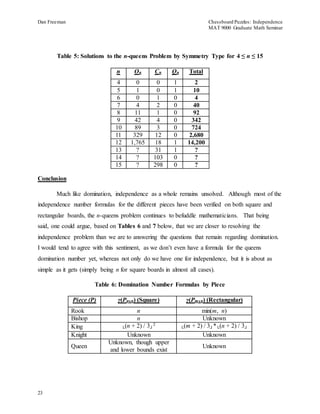
for 4 ≤ n ≤ 15, as shown in Table 5. Per the definitions above, the total number of solutions for
each value of n is 8On + 4Cn + 2Qn. As can be inferred from the fact that the number of solutions
to the problem for n = 13, 14 and 15 are unknown, much work still needs to be done to solve this
puzzle. Also worth pointing out is that the number of solutions decreases dramatically as the
level of symmetry increases. For example, there are a whopping 1,765 distinct ordinary
solutions to the 12-queens problem, but only 18 centrosymmetric solutions and just 1 doubly
centrosymmetric solution [1, pp. 175].

23
Table 5: Solutions to the n-queens Problem by Symmetry Type for 4 ≤ n ≤ 15
n On Cn Qn Total
4 0 0 1 2
5 1 0 1 10
6 0 1 0 4
7 4 2 0 40
8 11 1 0 92
9 42 4 0 342
10 89 3 0 724
11 329 12 0 2,680
12 1,765 18 1 14,200
13 ? 31 1 ?
14 ? 103 0 ?
15 ? 298 0 ?
Conclusion
Much like domination, independence as a whole remains unsolved. Although most of the
independence number formulas for the different pieces have been verified on both square and
rectangular boards, the n-queens problem continues to befuddle mathematicians. That being
said, one could argue, based on Tables 6 and 7 below, that we are closer to resolving the
independence problem than we are to answering the questions that remain regarding domination.
I would tend to agree with this sentiment, as we don’t even have a formula for the queens
domination number yet, whereas not only do we have one for independence, but it is about as
simple as it gets (simply being n for square boards in almost all cases).
Table 6: Domination Number Formulas by Piece
Piece (P) γ(Pnxn) (Square) γ(Pmxn) (Rectangular)
Rook n min(m, n)
Bishop n Unknown
King └(n + 2) / 3┘
2 └(m + 2) / 3┘*└(n + 2) / 3┘
Knight Unknown Unknown
Queen
Unknown, though upper
and lower bounds exist
Unknown

24
Table 7: Independence Number Formulas by Piece
Piece (P) β(Pnxn) (Square) β(Pmxn) (Rectangular)
Rook n min(n, m)
Bishop 2n – 2 Unknown
King └½*(n + 1)┘
2 └½*(m + 1)┘*└½*(n + 1)┘
Knight
4 if n = 2;
½*n2 if n ≥ 4, n even;
½*(n2 + 1) if n odd
n if m = 1, for all n;
2*(┌n / 4┐ + ┌(n – 1) / 4┐)
if m = 2, for all n;
┌½*mn┐ if m, n ≥ 3
Queen
1 if n = 2;
2 if n = 3;
n for all other n
1 if m = n = 2;
2 if m = n = 3;
min(m, n) for all other m, n
I do not see someone coming up with an ultimate formula for the number of permutations
of n independent queens on an nxn board anytime in the near future. I am not sure if that will
ever transpire, but I believe that as computers become more and more powerful, we will be able
to see more trends and patterns in large chessboards and hopefully be able to develop upper and
lower bounds for βPerm(Qnxn). In addition, studying the n-queens problem on rectangular boards,
something I have not come across in my research, would certainly be worthwhile in an attempt to
better understand this elusive puzzle.
In my next paper in this series, I will turn my attention to a completely different notion in
mathematical chessboard puzzles known as the knight’s tour. This is a classic problem and
studying it will help us realize the diversity of chessboard problems and how it relates to other
seemingly unrelated concepts in mathematics.

Sources Cited
[1] J.J. Watkins. Across the Board: The Mathematics of Chessboard Problems. Princeton, New
Jersey: Princeton University Press, 2004.
[2] J. DeMaio, W.P. Faust. Domination on the mxn Toroidal Chessboard by Rooks and Bishops.
Department of Mathematics and Statistics, Kennesaw State University.
[3] S. Wagon. Hex Graphs. Department of Mathematics, Statistics and Computer Science,
Macalester College.
[4] “Chess.” Wikipedia, Wikimedia Foundation. http://en.wikipedia.org/wiki/Chess
[5] A. Tamid. “Math Forum Discussions. ”
http://mathforum.org/kb/message.jspa?messageID=363988
25

Chessboard Puzzles Part 2 - Independence

More Related Content

Viewers also liked

Chessboard Puzzles Part 2 - Independence