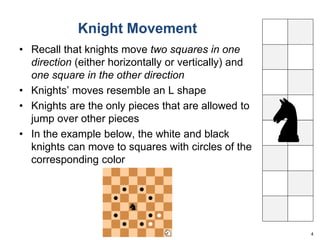
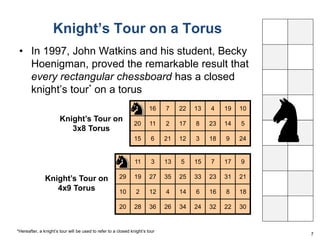
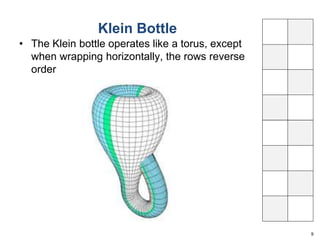
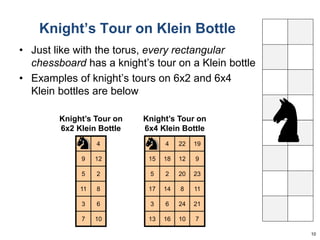
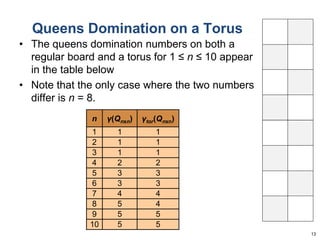
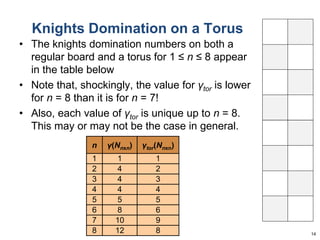
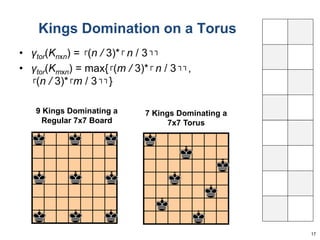
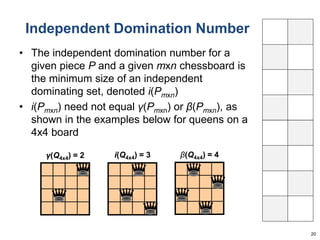
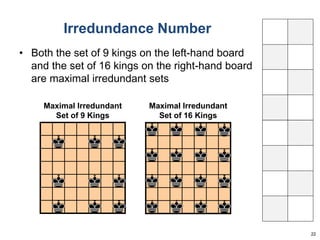
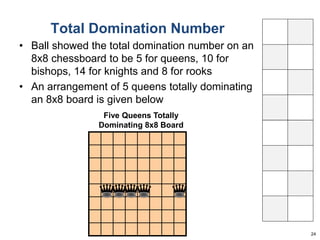
This document summarizes Dan Freeman's presentation on chessboard puzzles involving surfaces other than the standard chessboard. It discusses knight's tours, domination numbers, and other concepts on toroidal, cylindrical, Klein bottle, and Mobius strip surfaces. Key results include every rectangular board having a closed knight's tour on a torus, formulas for domination numbers of various pieces on these surfaces, and examples of puzzles on different board geometries.

1. Chessboard Puzzles
Part 4: Other Surfaces
and Variations
Dan Freeman
April 27, 2014
Villanova University
MAT 9000 Graduate Math Seminar

2. Any Questions from Last Time?
2

3. Introduction
• In the first three presentations, we looked at
the concepts chessboard domination,
chessboard independence and the knight’s tour
• Tonight we will conclude this series of
presentations with a look at these three
concepts on non-regular surfaces
• We will also touch on a few other concepts
associated with chessboard mathematics
3

4. Knight Movement
• Recall that knights move two squares in one
direction (either horizontally or vertically) and
one square in the other direction
• Knights’ moves resemble an L shape
• Knights are the only pieces that are allowed to
jump over other pieces
• In the example below, the white and black
knights can move to squares with circles of the
corresponding color
4

5. Knight’s Tour Revisited
• A knight’s tour is a succession of moves made
by a knight that traverse every square on a
chessboard once and only once
• There are two kinds of knight’s tours, a closed
knight’s tour and an open knight’s tour:
– A closed knight’s tour is one in which the knight’s last
move in the tour places it a single move away from
where it started
– An open knight’s tour is one in which the knight’s last
move in the tour places it on a square that is not a
single move away from where it started
5

6. Toroidal Chessboard
6
• A torus is a donut-shaped surface in which
both the rows and columns wrap around

7. Knight’s Tour on a Torus
• In 1997, John Watkins and his student, Becky
Hoenigman, proved the remarkable result that
every rectangular chessboard has a closed
knight’s tour* on a torus
7
1
16 7 22 13 4 19 10
20 11 2 17 8 23 14 5
15 6 21 12 3 18 9 24
Knight’s Tour on
3x8 Torus
Knight’s Tour on
4x9 Torus
11 3 13 5 15 7 17 9
1
29 19 27 35 25 33 23 31 21
10 2 12 4 14 6 16 8 18
20 28 36 26 34 24 32 22 30
*Hereafter, a knight’s tour will be used to refer to a closed knight’s tour

8. Knight’s Tour on a Cylinder
• Unlike a torus, a cylinder only wraps in one
dimension, not both
• In 2000, John Watkins proved that a knight’s
tour exists on an mxn cylindrical chessboard
unless one of the following two conditions
holds:
1) m = 1 and n > 1; or
2) m = 2 or 4 and n is even
• Here is why the above cases are excluded:
– If m = 1, a knight can’t move at all
– If m = 2 and n is even, then each move would take
the knight left or right by two columns and so then
only at most half of the columns would be visited
– If m = 4 and n is even, then the coloring argument by
Louis Pósa from the last presentation holds
8

9. Klein Bottle
9
• The Klein bottle operates like a torus, except
when wrapping horizontally, the rows reverse
order

10. Knight’s Tour on Klein Bottle
• Just like with the torus, every rectangular
chessboard has a knight’s tour on a Klein bottle
• Examples of knight’s tours on 6x2 and 6x4
Klein bottles are below
10
1 4
9 12
5 2
11 8
3 6
7 10
4 22 19
15 18 12 9
5 2 20 23
17 14 8 11
3 6 24 21
13 16 10 7
Knight’s Tour on
6x2 Klein Bottle
Knight’s Tour on
6x4 Klein Bottle
1 1

11. Möbius Strip
11
• A Möbius strip is like a cylinder in that it only
wraps in one dimension but is distinguished by
the half-twist it makes when wrapping, like the
Klein bottle

12. Knight’s Tour on Möbius Strip
12
• A knight’s tour exists on a Mobius strip unless
one or more of the following three conditions
hold:
1) m = 1 and n > 1; or n = 1 and m = 3, 4 or 5;
2) m = 2 or 4 and n is even
3) n = 4 and m = 3

13. Queens Domination on a Torus
• The queens domination numbers on both a
regular board and a torus for 1 ≤ n ≤ 10 appear
in the table below
• Note that the only case where the two numbers
differ is n = 8.
13
n γ(Qnxn) γtor(Qnxn)
1 1 1
2 1 1
3 1 1
4 2 2
5 3 3
6 3 3
7 4 4
8 5 4
9 5 5
10 5 5

14. Knights Domination on a Torus
• The knights domination numbers on both a
regular board and a torus for 1 ≤ n ≤ 8 appear
in the table below
• Note that, shockingly, the value for γtor is lower
for n = 8 than it is for n = 7!
• Also, each value of γtor is unique up to n = 8.
This may or may not be the case in general.
14
n γ(Nnxn) γtor(Nnxn)
1 1 1
2 4 2
3 4 3
4 4 4
5 5 5
6 8 6
7 10 9
8 12 8

15. Rooks Domination on a Torus
• Since it doesn’t make any difference whether a
rook is on a regular board or on a torus, it
follows that γ(Rnxn) = γtor(Rnxn) = n
15

16. Bishops Domination on a Torus
• Since the number of distinct diagonals in either
direction drops from 2n – 1 to n on a torus, it is
easy to see that γtor(Bnxn) = n, just like
γ(Bnxn) = n
16
n Distinct Diagonals on
a Torus Shown in Red

17. Kings Domination on a Torus
• γtor(Knxn) = ┌(n / 3)*┌ n / 3 ┐┐
• γtor(Kmxn) = max{┌(m / 3)*┌ n / 3 ┐┐,
┌(n / 3)*┌m / 3 ┐┐}
17
9 Kings Dominating a
Regular 7x7 Board
7 Kings Dominating a
7x7 Torus

18. Kings Independence on a Torus
• The formulas for the kings independence
number on a torus are analogous to those for
the kings domination number
• βtor(Knxn) = └(½*n)*└½*n┘┘
• βtor(Kmxn) = min{└(½*m)*└ ½*n ┘┘,
└(½*n)*└ ½*m┘┘}
18

19. n-queens Problem on Cylinder
• A formula for βcyl(Qnxn) has not yet been found
• While βcyl(Q5x5) = β(Q5x5) = 5 and βcyl(Q7x7) =
β(Q7x7) = 7, βcyl(Q8x8) = 6 ≠ β(Q8x8) = 8
• The picture below shows why 8 queens fail to
be independent on an 8x8 cylinder
19
8 Queens Fail to Be
Independent on 8x8 Cylinder

20. Independent Domination Number
• The independent domination number for a
given piece P and a given mxn chessboard is
the minimum size of an independent
dominating set, denoted i(Pmxn)
• i(Pmxn) need not equal γ(Pmxn) or β(Pmxn), as
shown in the examples below for queens on a
4x4 board
20
γ(Q4x4) = 2 i(Q4x4) = 3 β(Q4x4) = 4

21. Irredundance Number
• An irredundant set of chess pieces is one in
which each piece in the set either occupies a
square that is not covered by another piece or
else it covers a square that no other piece
covers
• A maximal irredundant set is one that is not a
proper subset of any irredundant set
• The irredundance number for a given piece P
and a given mxn chessboard is the minimum
size of a maximal irredundant set
21

22. Irredundance Number
• Both the set of 9 kings on the left-hand board
and the set of 16 kings on the right-hand board
are maximal irredundant sets
22
Maximal Irredundant
Set of 9 Kings
Maximal Irredundant
Set of 16 Kings

23. Total Domination Number
• W.W. Rouse Ball introduced the concept of
total domination in 1987
• The total domination number is the minimum
number of pieces of a given type P on a given
mxn chessboard that are required to attack
every square on the board, including occupied
ones
23

24. Total Domination Number
• Ball showed the total domination number on an
8x8 chessboard to be 5 for queens, 10 for
bishops, 14 for knights and 8 for rooks
• An arrangement of 5 queens totally dominating
an 8x8 board is given below
24
Five Queens Totally
Dominating 8x8 Board

25. Sources Cited
• J.J. Watkins. Across the Board: The Mathematics of
Chessboard Problems. Princeton, New Jersey:
Princeton University Press, 2004.
25