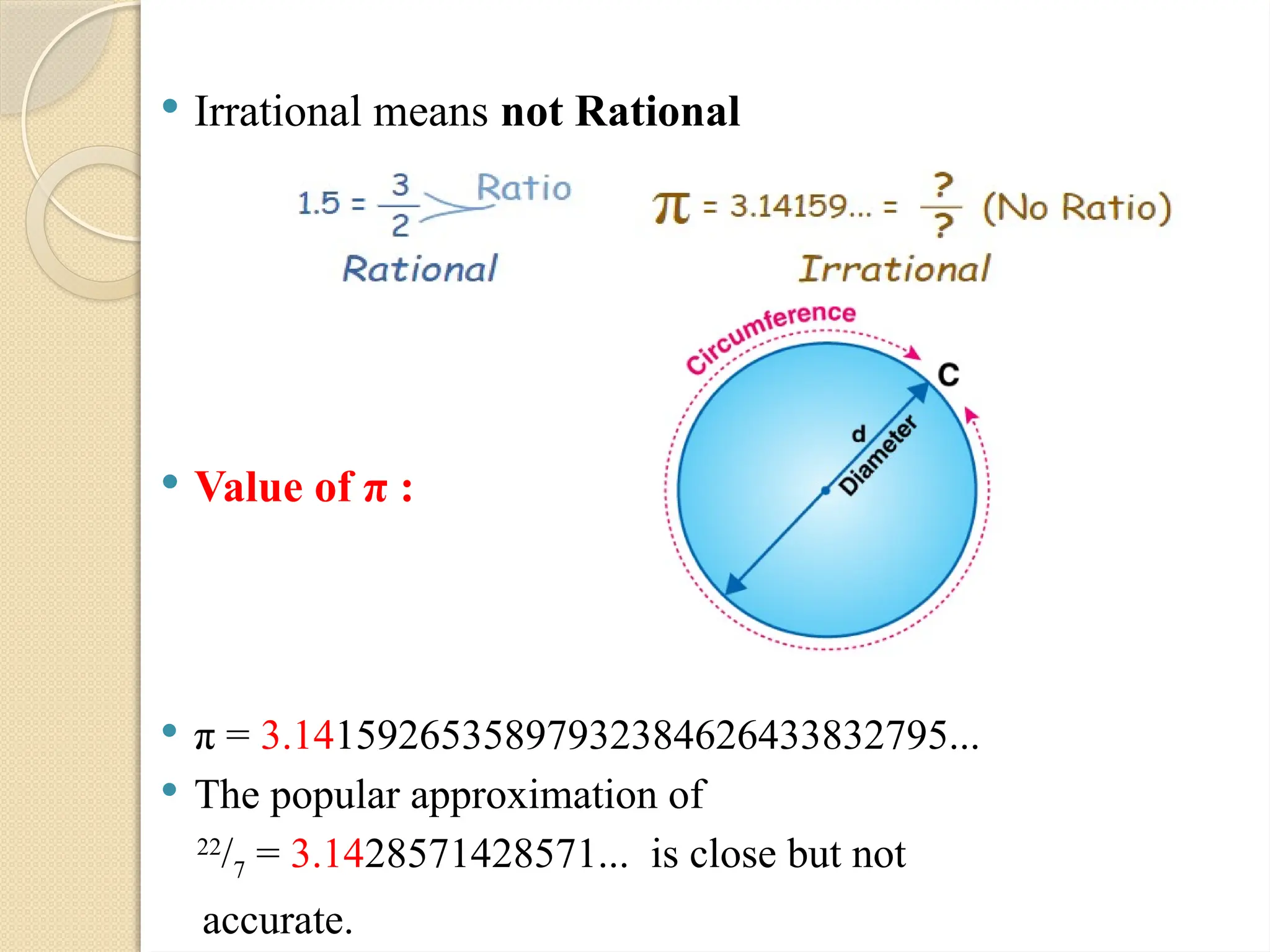
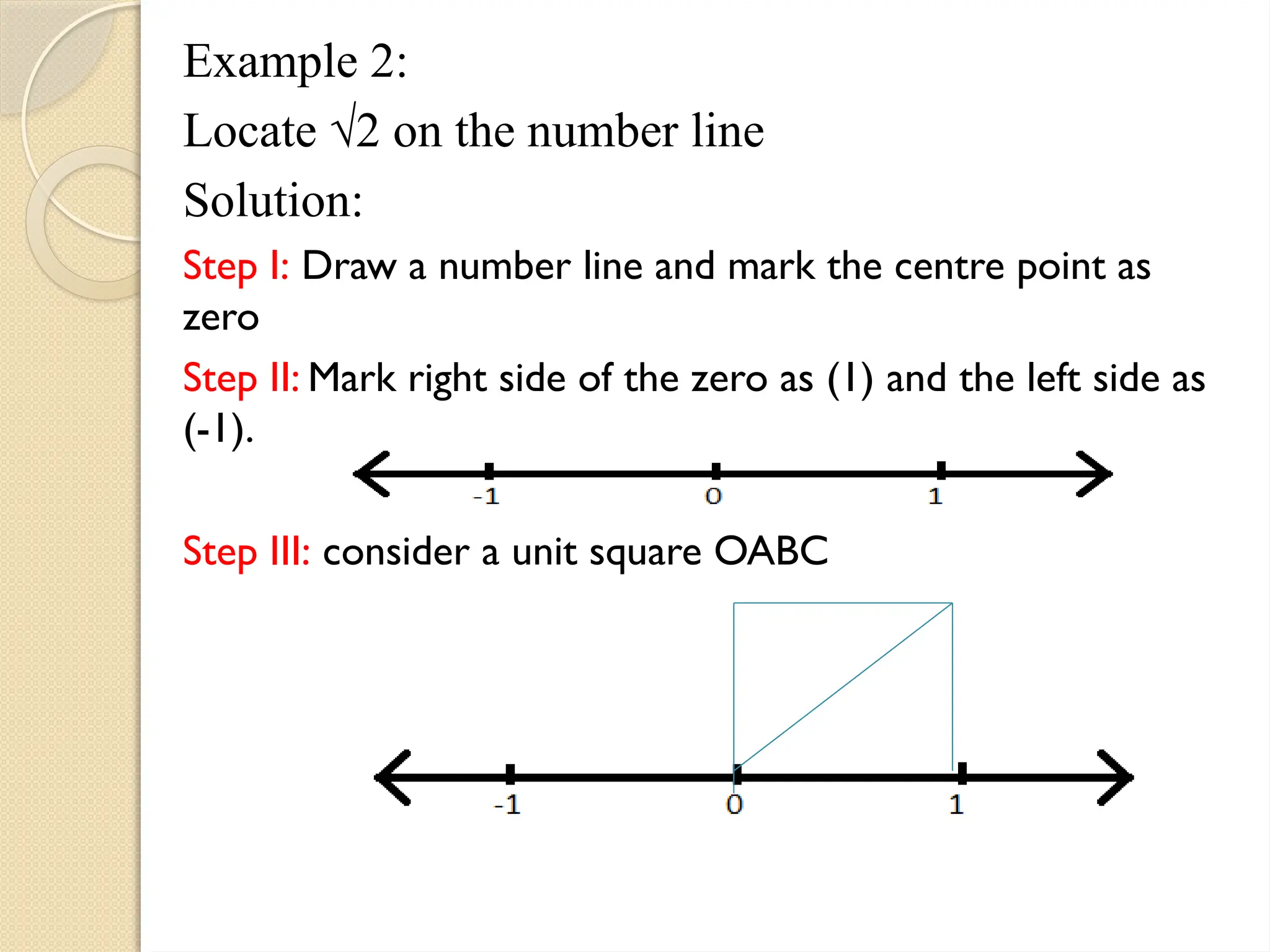
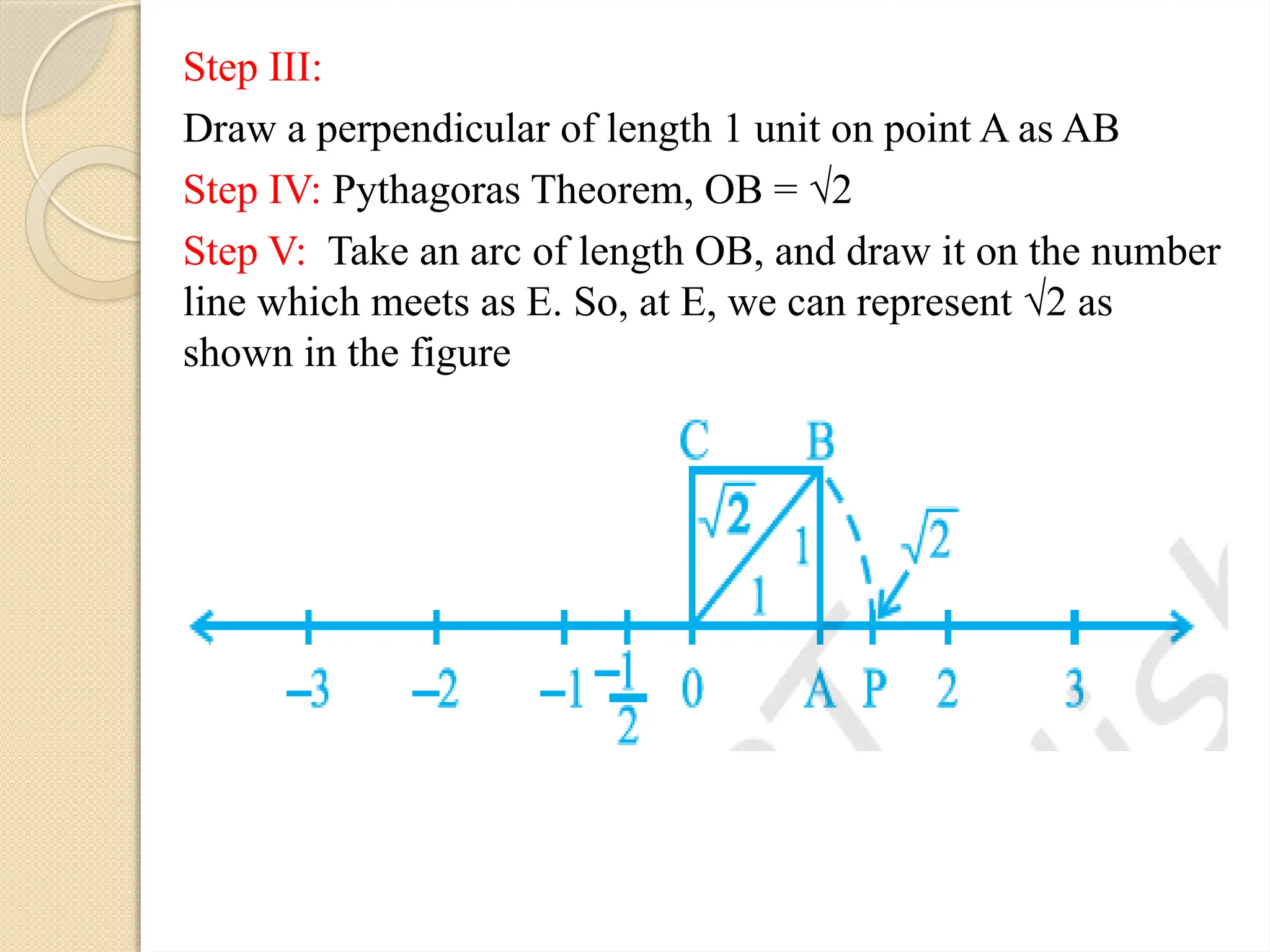
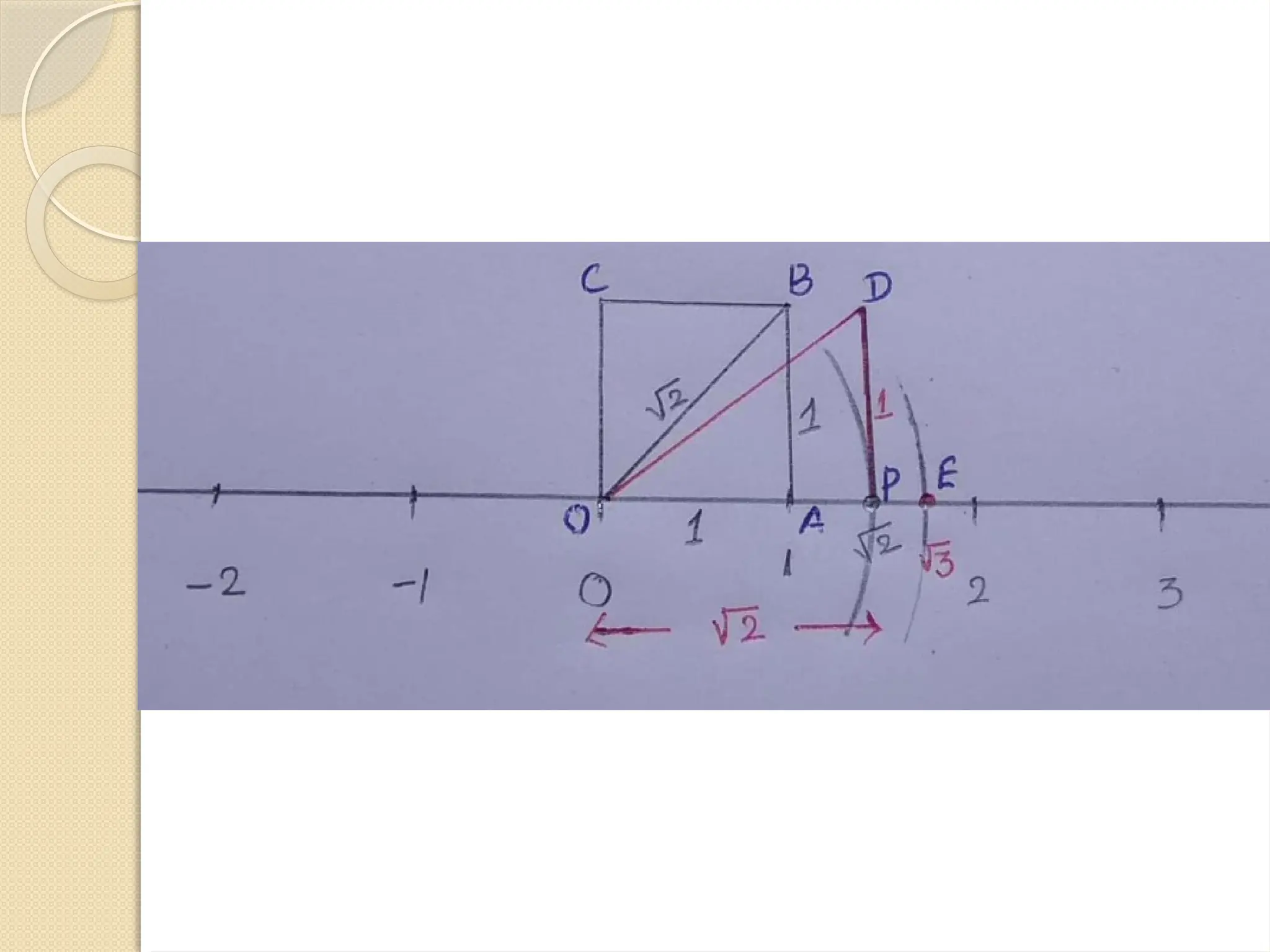
The document discusses irrational numbers, first discovered by the Pythagoreans around 400 BC, defining them as numbers that cannot be expressed as the ratio of integers. It explains their characteristics, such as non-terminating, non-recurring decimal expansions with examples like √2 and π. Additionally, it provides methods for locating square roots of irrational numbers on a number line using the Pythagorean theorem and includes exercises for further understanding.

1. NUMBER SYSTEMS
 Irrational Number
Presented by
Dr.T.Gandhimathi
Associate Professor of Mathematics
P.A.C.E.T, Pollachi

2. History of Irrational Number
 The Pythagoreans in Greece, followers of the
famous mathematician and philosopher
Pythagoras, were the first to discover the
numbers which were not rationals, around 400
BC.
 These numbers are called irrational
numbers(irrationals), because they cannot be
written in the form of a ratio of integers.

3. Definition
 The number ‘s’ which cannot be written in the
form of p/q is called irrational, where p and q
are integers and q ≠ 0 or the numbers which are
not rational are called Irrational Numbers
 The decimal expansion of an irrational number
is non-terminating and non-recurring
 Example :
√2, √11,  , 0.10110111011110...

4.  Irrational means not Rational
 Value of π :
 π = 3.1415926535897932384626433832795...
 The popular approximation of
22
/7 = 3.1428571428571... is close but not
accurate.

5. Example 1:
Find the value of √2
Solution:

6. Pythagoras Theorem
In a right-angled triangle, the square of the
hypotenuse side is equal to the sum of squares of the
other two sides

7. Example 2:
Locate √2 on the number line
Solution:
Step I: Draw a number line and mark the centre point as
zero
Step II: Mark right side of the zero as (1) and the left side as
(-1).
Step III: consider a unit square OABC
Oo

8. Step III:
Draw a perpendicular of length 1 unit on point A as AB
Step IV: Pythagoras Theorem, OB = √2
Step V: Take an arc of length OB, and draw it on the number
line which meets as E. So, at E, we can represent √2 as
shown in the figure

9. Example 3:
Locate √3 on the number line
Solution:
Step I: Draw a √2 on number line
Step II: Construct PD of unit length perpendicular to
OP
Step III: using the Pythagoras theorem,
OD = = √3
Step IV: Using a compass, with centre O and radius
OD, draw an arc which intersects the number line at
the point E.
Step V: Then E corresponds to √3 .
....DocumentsRepresent Root 3 on Number line -
YouTube (480p).mp4

11. EXERCISE 1.2
1. State whether the following statements are true or
false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form √m
where m is a natural number.
(iii) Every real number is an irrational number.
Solution:
(i) True
(ii) False
(iii) False

12. 2. Are the square roots of all positive integers
irrational? If not, give an example of the square root
of a number that is a rational number
Solution:
The square roots of all positive integers are not
irrational.
Example: √4 = 2, 2 is a rational.
Homework:
3. Show how √5 can be represented on the number
line.
4. Locate √10 on the number line

13. Thank you