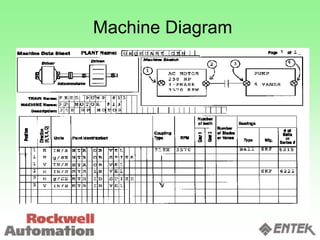
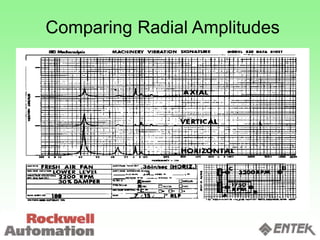
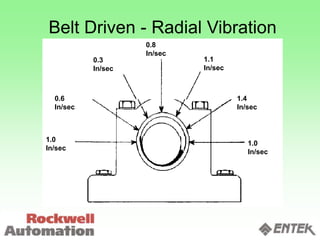
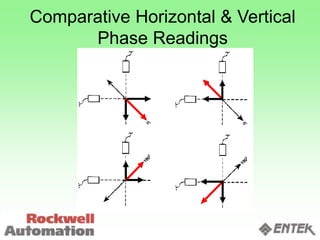
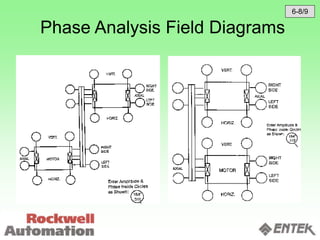
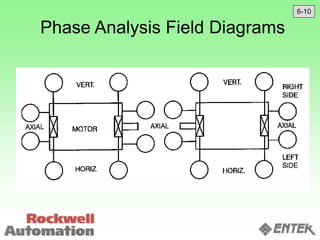
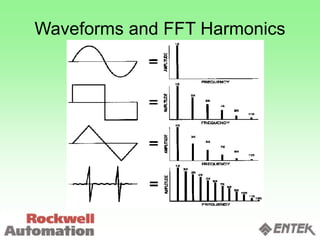
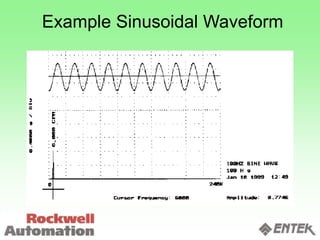
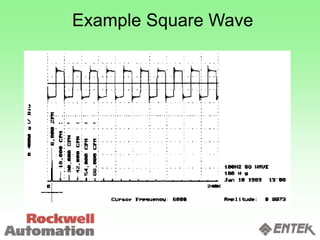
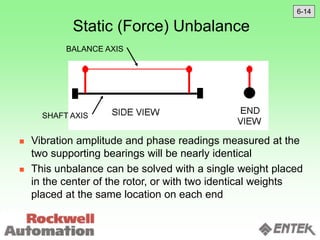
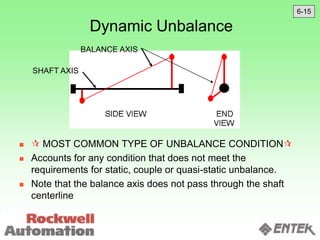
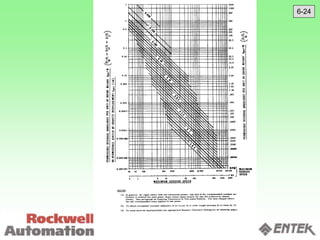
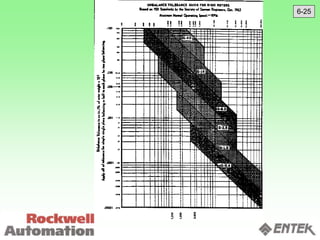
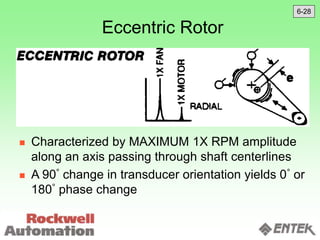
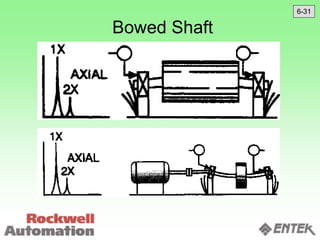
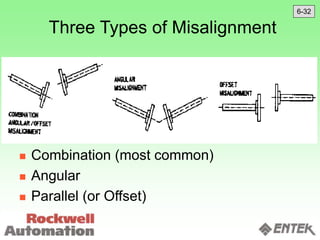
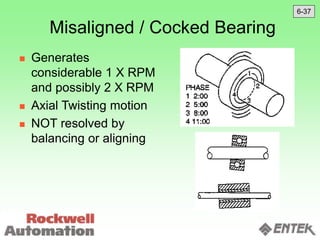
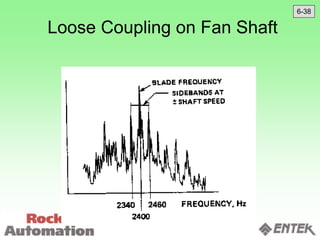
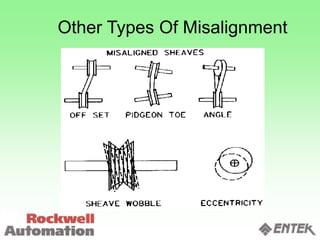
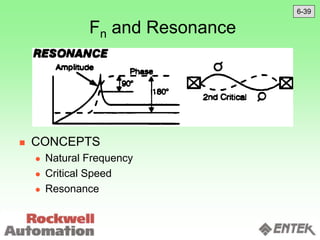
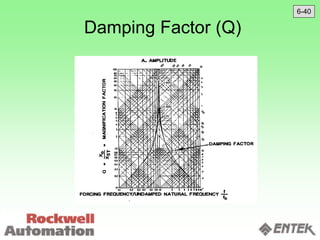
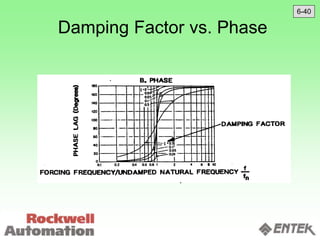
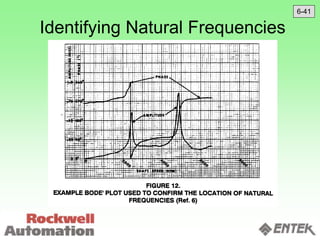
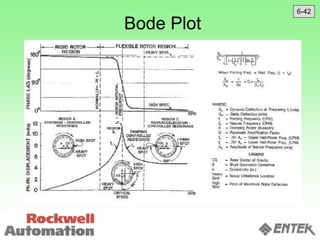
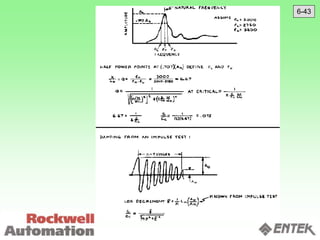
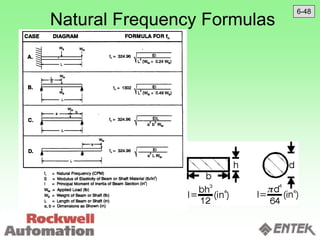
This document discusses vibration analysis and diagnostics. It outlines an 8 step analysis procedure including defining the problem, determining machine history and details, visual inspection, data collection, frequency confirmation, vibration direction/phase analysis, and probing studies. Specific vibration issues covered include unbalance, resonance, misalignment, bent shafts, and component failures. Diagnosing the root cause involves analyzing vibration frequency spectra and amplitudes across machine components.

1. Chapter 6
Vibration Spectrum Analysis & Diagnostics
(Part 1)
(Unbalance - Resonance)

2. Analysis
A Logical Process
 What is the problem ?
 What are the symptoms ?
 What machine information do I have ?
 What data should I take ?
 Where should I take data ?

3. Eight Step Analysis Procedure
 1 - Define the Problem
 2 - Determine the Machine History
 3 - Determine the Machine Details
 4 - Visual Inspection
 5 - Data Collection
 6 - Frequency Confirmation
 7 - Vibration Direction / Phase
 8 - Probing Studies

4. Step 1 - Define the Problem
 Bearing, seal, or other frequent component
failures
 Structural failures
 Inability to manufacture a quality product
(machine tools)
 Physical annoyance / noisy
 Vibration is excessive
 Does not meet performance standards
 (API, ISO, AGMA, etc.)

5. Step 2 - Determine Machine History
 When did the problem start?
 It’s always been rough
 The vibration has gradually increased over a period of
time
 The vibration increased abruptly
 Have any changes been made?
 Repairs or parts replaced?
 Modifications?
 Machine speed?
 Load or product?
 Is the vibration temp. related?

6. Step 3 - Determine Machine Details
 Machine RPM(s)
 Type of bearings
 For rolling element
bearings
 number of rolling
elements (balls), ball
and pitch diameter
 or, Mfgr and model
 For fluid film bearings -
bearing configuration
 Number of fan blades
 Number of impeller vanes
 Number of gear teeth
 Coupling type
 Machine critical speeds
 Background sources
 Baseline data

7. Machine Diagram

8. Step 4 - Visual Inspection
 Loose, worn, or broken parts
 Rotor wear or deposit build-up
 Leaking seals
 Cracks in the base, foundation,broken
welds
 “Slow motion” study of rotor, belts, pulleys,
coupling, etc., with strobe light

9. Step 5 - Data Collection
 Obtain tri-axial amplitude vs. frequency plots at
each bearing of the machine train
 Unless the analyst is very comfortable with mixed
scales, use same amplitude scale (range) for all plots
 For machine tools, analyze with:
 The machine shut down to evaluate background
sources
 The machine idling (no machining) to identify drive
related problems
 Under machine conditions to identify vibration from the
actual cutting, drilling or grinding operation (chatter)

10. Step 6 - Frequency Confirmation
 Determine if vibration frequencies are
EXACTLY related to machine RPM(s)
using:
 Strobe light
 Time-Synchronous averaging
 High resolution FFT
 Fmax 0-12,000 CPM
 #FFT Lines - 3200 (minimum)

11. Step 6 - Frequency Confirmation
 Fmax needs to be high enough to catch all
defect frequencies in machine
 Resolution needs to be sharp enough to
separate closely spaced frequencies
 Some machines may require more than
one set of FFT’s in order to capture all
problem frequencies with sufficient
resolution for analysis

12. Identifying the Problem Based on
Frequency
 Many vibration
problems generate
frequencies related to
the rotating speed or
harmonics
 Look for bearing and
electrical vibration

13. Step 7 - Vibration Direction / Phase
 Determine if the vibration is directional or
non-directional by:
 Comparing the horizontal and vertical phase
readings
 Taking radial vibration amplitude readings
every 30° around each bearing

14. FFT’s Should Be Compared by
Direction: H,V,A
 How do radial (horizontal and vertical)
readings compare to each other
 How do radial readings compare with axial
measurements

15. Comparing Radial Amplitudes

16. Comparing Radial And Axial
Measurements
 Only a few machine defects can cause high
axial readings
 These include Misalignment, Bent Shafts, or
Unbalance of Overhung Rotors
 General Rule:
 Any time the axial amplitude exceeds 50% of
the highest radial, these defects should be
strongly considered

17. Belt Driven - Radial Vibration
1.0
In/sec
0.6
In/sec
0.3
In/sec
0.8
In/sec
1.1
In/sec
1.4
In/sec
1.0
In/sec

18. Comparative Horizontal & Vertical
Phase Readings

19. Phase Analysis Field Diagrams
6-8/9

20. Phase Analysis Field Diagrams
6-10

21. Step 8 - Probing Studies
 Base/foundation
 Piping and other related components
 Across all mounting interfaces
 Background machinery

22. Waveforms and FFT Harmonics

23. Example Sinusoidal Waveform

24. Example Square Wave

25. Unbalance
Types, Symptoms, and Correction
6-11

26. Rotor Unbalance Characteristics
Can Only Cause 1X RPM Vibration 
 WARNING: 1X not ALWAYS from unbalance
 Amplitude proportional to distance between
center of mass and center of rotation
 Uniform rotating force, changing in direction
and evenly applied radially
 since mobility or “dynamic sensitivity” may
differ between H and V axes, amplitudes may
also differ
6-12

27. Rotor Unbalance Characteristics
 A dominant unbalance shows 90° phase
difference between H and V
 within usual 30° tolerance
 Horizontal phase difference between
inboard and outboard bearings should
match vertical phase difference
 Radial vibration much greater than axial
vibration
 Overhung rotors are the exception
6-12

28. Rotor Unbalance Characteristics
 Repeatable phase in all directions
 except for minor beats and “chasing” phases
when balance has been largely corrected
 May be amplified by resonance
 May be the force behind the evidence of
looseness
6-12

29.  Static Unbalance
 The central principal axis is displaced parallel to the shaft axis
 The unbalance is even at both ends, and is in the same direction
 Couple Unbalance
 The central principal axis intersects the shaft axis at the rotor
center of gravity
 The unbalance is even at both ends, but in the opposite direction
 Quasi-Static Unbalance
 A combination of static and couple unbalance where central
principal axis intersects the shaft axis, but NOT at the rotor center
of gravity
 Dynamic Unbalance
 A random combination of static and couple unbalance
 The centerline of unbalance does not intersect the centerline of
the shaft
Types Of Unbalance
6-11

30. Phase & Unbalance
6-13

31. Static (Force) Unbalance
SHAFT AXIS
BALANCE AXIS
 Vibration amplitude and phase readings measured at the
two supporting bearings will be nearly identical
 This unbalance can be solved with a single weight placed
in the center of the rotor, or with two identical weights
placed at the same location on each end
6-14

32.  Vibration amplitudes will be reasonably the
same, but phase readings at the bearings will
differ by 180°
 This unbalance can be solved with identical
weights placed at each end of the rotor 180°
apart
Coupled Unbalance
SHAFT AXIS
BALANCE AXIS
6-15

33. Quasi-Static Unbalance
SHAFT AXIS
BALANCE AXIS
 A Static (or Coupled) Unbalance where vibration
amplitudes at one support are considerably
higher than the other and phase readings are the
same (or differ by 180°)

34.   MOST COMMON TYPE OF UNBALANCE CONDITION
 Accounts for any condition that does not meet the
requirements for static, couple or quasi-static unbalance.
 Note that the balance axis does not pass through the shaft
centerline
Dynamic Unbalance
SHAFT AXIS
BALANCE AXIS
6-15

35. Cross Effect
 A heavy spot of unbalance located at one
end of a rotor will not only create unbalance
vibration at that end, but will also create
some unbalance vibration at the opposite
end of the rotor as well

36. Overhung Rotors
 Axial often greater than
radial
 due to couple effect
 Inboard axial phase
should equal outboard
axial phase
 Usually corrected by:
 Static first:
 Brg 2, Plane A
 Then coupled:
 Brg 1, Equal weights in
Planes A and B, 180° apart
6-16

37. Residual Unbalance
 Rotor Sensitivity =
 Trial Wt. Size X Mounting Radius
Trial Wt. Effect (amplitude)
 Trial weight effect is measured through the
vector length in the vector diagram
calculation during balancing
 Residual Unbalance =
 Rotor Sensitivity X Final Balance Amplitude
6-21

38. ISO-1940 Balance Grades
6-23

39. ISO-1940 Balance Grades 6-23

40. 6-24

41. 6-25

42. A Tolerable Residual
Unbalance for Modern
General Purpose Machines...
To satisfy MIL-STD and API, we should
meet ISO 1940 G 2.5
6-20

43. ISO 1940 G(rade) 6.3
 Means 6.3 mm/sec Peak
 Corresponds to  0.25 in/sec Peak
 NOT AN ACCEPTABLE STANDARD for
General Purpose Machines in 2000 and
beyond
 G 2.5 corresponds to  0.1in/sec Peak
 This balance specification should be readily
achievable (for most machines) using modern
equipment and balancing techniques
6-20

44. Eccentric Rotors
The physical center of the shaft does
not line up with the rotational centerline
of the shaft
6-27

45.  Characterized by MAXIMUM 1X RPM amplitude
along an axis passing through shaft centerlines
 A 90° change in transducer orientation yields 0° or
180° phase change
Eccentric Rotor
6-28

46. Eccentric Behavior
 Gears have variation in mating force along
centerline of gears
 Sheaves have vibration along centerline of
driver and driven pulley
 Eccentric Motor Armature causes moving
unbalanced magnetic forces
 2X Line Freq. And Pole Pass Freq.
 Eccentric Stator will show a line of maximized
vibration
 Eccentric bearings rarely cause a problem
because of precision manufacture
 when reaching late stages of deterioration, a
bearing may exhibit eccentric behavior
 Eccentric impellers may cause a hydraulic
unbalance between stationary and moving
vanes (high vibration at BPF and harmonics)
6-28

47. Eccentric Rotors
 Balancing attempts may cause a drop of
amplitude in one radial direction with a
simultaneous increase in another
 May cause significantly HIGHER vibration
in one radial direction than another
6-29

48. Bent or Kinked Shaft
Kinked - Bent at or near one bearing
Bent - Uniform bow between bearings
6-30

49. Bent Shaft
 Common causes of a bent shaft
 Manufacturing or machining errors
 Mishandling during transportation
 “Bow” due to thermal growth or uneven heating
due to rotor bar problems
 Sag from sitting in one spot for extended time
 Two types of bent shaft
 Kinked Shaft - Bend is at or near one bearing
 Bowed Shaft - Bend is uniform between two
bearings
6-30

50. Bent Shaft Symptoms
 Predominant vibration is at 1 X RPM. This
can be accompanied by a 2 X RPM peak
 Axial vibration amplitude normally exceeds
50% of highest radial amplitude
 Radial vibration is usually uniform
 Axial phase analysis must be used to verify
problem and type of bend
6-30

51. Identifying a Kinked Shaft
 Produces a twisting motion of the bearing
 Axial phase readings taken 90° apart will produce
a phase shift of 90°.
6-31

52. Bowed Shaft
6-31

53. A Critical Speed LOOKS like a Bent
Shaft
 A rotor operating close to or at a critical
speed may exhibit “bent shaft” behavior
 Shaft deflection is possibly imitating bent
shaft behavior
6-31

54. Electric Motors
 A growing vibration amplitude may indicate
shorted laminations…
 the localized heating imposes a shaft bend
as the rotor heats up
 may straighten or not, depending on whether
the bending exceeds elastic limits (reaches
permanent or plastic limits)
6-31

55. Misalignment
Still the most common source of vibration
(except in plants where PM has been successful
and laser alignment fully implemented)
6-32

56. Three Types of Misalignment
 Combination (most common)
 Angular
 Parallel (or Offset)
6-32

57. Misalignment
  MOST COMMON PROBLEM FOUND INITIALLY 
 Temperature changes can affect alignment
 Machines aligned cold can go out when warm
 Different expansion rates in the driver and driven bases can
cause misalignment with changes in ambient temperature
 Bases or foundations can settle
 Shims or bases can rust or corrode
 Grouting can shrink or deteriorate
 May increase energy demands
 More likely to be visible as an increase in RPM when
aligned correctly (power to product, not problem)
6-32

58. Misalignment (Cont.)
 Resulting forces are shared by driver and driven (not
localized)
 Differences in mass and stiffness may cause different
amplitudes on the driver and the driven, but the frequencies
will be present on both
 The level of misalignment severity is determined by
the machine’s ability to withstand the misalignment
 If the coupling is stronger or more pliable (can withstand
more misalignment) than the bearings, the bearings can fail
with little or no damage to the coupling
 A coupling’s ability to withstand more misalignment does not
reduce the higher forces resulting from this misalignment. It
merely transfers these higher forces to the bearings
6-32

59. Thermal Growth Rule of Thumb
 On start-up, vibration should start high and
ease up
 the pre-set “misalignment” eases as thermal
growth is achieved
 the machine “grows” (or “shrinks” for cryogenic
applications) into alignment
 Applicable to machines with significant thermal
growth

60. Symptoms Of Misalignment
 Radial vibration is highly directional
 1X RPM, 2 X RPM, and 3 X RPM can be present, IN
ANY COMBINATION, depending on the type and extent
of misalignment
Misalignment Symptom Direction
Angular 1X RPM Axial
Parallel 2 X RPM Radial (H & V)
Combination 1/2/3 X RPM Radial and Axial
 Problems internal to the coupling usually generate a 3 X
RPM vibration.
6-33

61. Symptoms are a function of...
 Coupled system’s ability to accommodate
misalignment
 Offset
 Speed
 Torque
 Corrosion, sludging and other factors
affecting coupling stiffness
6-33

62. Component Failure
 Coupling versus bearing
 the stiffer component wins out and survives
 Gears
 Belts
 Sheaves
 Blades
 Etc...

63. Outboard End - Possible Symptom
 The bearing next to the coupling may act
as a PIVOT
 relative to machine / bearing stiffness
 This may mean a stabilized INBOARD
bearing and severe vibration AWAY from
the coupling
6-32

64. Other Sources of High AXIAL Vibration
 ANGULAR misalignment
 Bent or kinked shaft
 Misaligned bearings
 Axial resonance
 Worn thrust bearings
 Worn helical or bevel gears
 Motor hunting for magnetic center (sleeve bearings)
 Couple unbalance or couple component of unbalance
 Highly pronounced on overhung rotors
6-33

65. PHASE ANALYSIS IS
ESSENTIAL
To assess misalignment or other
abnormal or excessive 1X, 2X and 3X
RPM vibration behavior
6-33

66. Angular Misalignment
 Produces predominant 1 X RPM peak in the axial
direction, with an elevated 2 X RPM possible
 Marked by 180 phase shift across the coupling in the
axial direction
 Axial forces cycle from max to min once per revolution
 Radial forces remain relative uniform throughout revolution
6-35

67. Parallel Or Offset Misalignment
 Produces a predominant 2 X RPM peak in the radial
spectrum
 Marked by 180 phase shift across the coupling in the
radial direction.
 Axial forces remain relative uniform throughout revolution
 Radial forces cycle from max to min twice each revolution
6-36

68. Very Pronounced Parallel
Misalignment on a SINGLE AXIS
 May cause behavior similar to other highly
directional vibration
 might be mistaken for resonance, eccentricity
or the like…
 Highly elliptical shaft orbit (flattened)
6-36

69. Misalignment Vs. Type C
Looseness
Excessive misalignment (whether
angular or parallel) may generate a
progressively HIGHER number of
running speed harmonics
6-36

70. Misaligned / Cocked Bearing
 Generates
considerable 1 X RPM
and possibly 2 X RPM
 Axial Twisting motion
 NOT resolved by
balancing or aligning
6-37

71. Coupling Problems
Reminder: seen in a MISALIGNMENT
context
6-37

72. Coupling Problems
 Long or short spacer
 noticeable radial 3 X RPM vibration
 much HIGHER axial 3 X RPM vibration
 Gear Type Lock-up
 may cause thrust bearing failure
 mostly 1X RPM with axial > radial
 when misalignment is present
 some mesh (# of grid X RPM) & harmonics
 Christmas Tree (2 X to 6 X, decreasing by 25% for
each harmonic increment
6-38

73. Coupling Problems
 Loose Coupling
 sidebands around BPF or GMF
 Text: “does not drive rotor at uniform speed
(RPM)”
 when torque is applied continuously, looseness will
not be manifest unless severe misalignment is
present
 Modulation mostly due to occasional shift of
coupling causing a pivoting effect resulting in
eccentric placement of the rotor within casing
6-38

74. Loose Coupling on Fan Shaft
6-38

75. Other Types Of Misalignment

76. Natural Frequency (Fn)
and Resonance
The Importance of Natural
Frequencies
6-39

77. Fn and Resonance
 CONCEPTS
 Natural Frequency
 Critical Speed
 Resonance
6-39

78. Fn and Resonance
 Every machine element has natural
frequencies based on mass, shape and
stiffness
 Resonance occurs when a forcing
frequency coincides with one of these
natural frequencies
6-39

79. VIBRATION DUE TO RESONANCE
 Every object, including every element or part of a
machine, has “natural frequencies” at which “it likes to
vibrate”
 Determined by machine mass and stiffness as well as moment
of inertia (shape) for the concerned axis
 CAN NOT CAUSE VIBRATION , it merely serves
as a “mechanical amplifier” (10x-100x)
 Resonance is a very common cause of excessive
vibration because:
 Machines consist of many individual elements
 Stiffness of each machine component differs in all directions,
meaning several natural frequencies within the range of the
generated forcing frequencies
6-39

80. Identifying Resonance
 Vibration will be highly directional
 Changing the exciting forcing frequency to
observe reaction
 Change the mass or stiffness of the
suspected resonant machine component
 Perform a bump test
 modally tuned hammer test
6-39

81. FORCING FREQUENCIES
 Almost ANY frequency present in the
spectrum can become a forcing frequency
 Unbalance, misalignment, torque or blade
pass pulses, harmonics of each, etc.
6-39

82. 6-40
Damping Factor (Q)

83. 6-40
Damping Factor vs. Phase

84. 6-40
Amplification Formula

85. Identifying Natural Frequencies
6-41

86. Bode Plot
6-42

87. 6-43

88. How to Resolve Resonance Problems
 Change stiffness
 Change mass
 Add isolation
 Add damping material
 Install Tune Damper (Vibration Absorber)
 Precision Balancing (last resort)
6-47

89. Natural Frequency Formulas
6-48