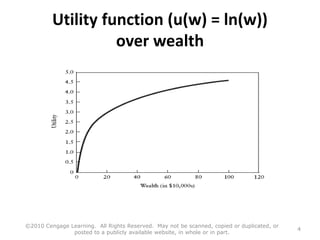
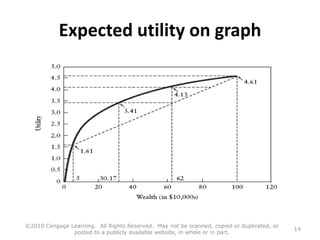
This document summarizes key concepts from expected utility theory. It outlines the theory's assumptions that people have rational preferences, maximize utility, and make independent decisions based on information. Preferences are defined as complete and transitive. Expected utility theory says individuals should act to maximize expected utility when making decisions under risk. It provides an example calculation and discusses properties like risk aversion. However, the document notes that expected utility theory has problems accounting for all observed behaviors.

1. Chapter 1: Foundations of Finance I:
Expected Utility Theory
Powerpoint Slides to accompany Behavioral
Finance: Psychology, Decision-making and Markets
by Lucy F. Ackert & Richard Deaves
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated,
or posted to a publicly available website, in whole or in part.
1

2. Neoclassical economics
1. People have rational preferences across
possible outcomes or states of nature.
2. People maximize utility and firms maximize
profits.
3. People make independent decisions based
on all relevant information.
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
2

3. Preferences and utility function
• Two key assumptions about preferences:
– Completeness (ordering)
– Transitivity
• Utility over goods:
u(2 bread, 1 water) > u(1 bread, 2 water)
• Utility over money:
u(w2) > u(w1) if w2 > w1
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
3

4. Utility function (u(w) = ln(w))
over wealth
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
4

5. Expected utility theory
• Says that individuals should act when
confronted with decision-making under
uncertainty in a certain way.
• Theory is really set up to deal with risk, not
uncertainty:
– Risk is when you know what the outcomes could be,
and can assign probabilities
– Uncertainty is when you can’t assign probabilities; or
you can’t come up with a list of possible outcomes
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
5

6. Wealth outcomes
• Say there are a given number of states of the world:
– A. rain or sun
– B. cold or warm
– Leading to 4 states: e.g., rain and cold
• And individuals can assign probabilities to each of these
states:
– Probability of rain+cold is .1, etc.
• Say income (or wealth) level can be assigned to each state of
world. Think of an ice cream vendor:
– Rain+cold: $100/day
– Sun+warm: $500/day
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
6

7. Prospects
• A prospect is defined as a series of wealth or
income levels and associated probabilities.
• Example:
– $500 with probability .8
– $2,000 with probability .2
– P1(.8, 500, 2,000)
• When 2nd option is zero, let’s write:
– P2(.8, 500)
• Expected utility theory comes from a series of
assumptions (axioms) on these prospects.
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
7

8. Transitivity and completeness of
preferences over prospects
• Consider two more prospects P3 and P4:
– P3(.7, 300, 2,100)
– P4(.5, 600, 2,000)
• An ordering of P1 vs. P3 and P1 vs. P4 could
be:
• P1 P3 and P4 P1
• Transitivity says: P4 P3
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
8

9. Expected utility
• Say one has to choose between two prospects.
• Based on assumptions such as ordering and
transitivity (and others), it can be shown that
when such choices over risky prospects are to be
made, people should act as if they are
maximizing expected utility:
U(P) = pr A * u(wA) + (1-pr A) * u(wB)
• Can generalize to more than two outcomes:
U(P) = pr A * u(wA) + pr B * u(wB) + pr C * u(wC)
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
9

10. Expected utility example
• u(w) = w.5
• Prospects:
– P5(.5, 1000, 500)
– P6(.6, 1200, 300)
• For P5: U(P5) = .5 * 1000.5 + .5 * 500.5 = 26.99
• For P6: U(P6) = .6 * 1200.5 + .4 * 300.5 = 27.71
• So P6 P5.
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
10

11. Properties of utility functions
• Certain properties of utility functions can be
demonstrated:
– Upward-sloping
– Unique up to a positive linear transformation
• Latter allows one to set u(lowest outcome)=0 and u(highest
outcome)=1, which can be useful for proving certain things
• Other properties such as differentiability
(implying continuity) are often assumed.
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
11

12. Risk aversion assumption
• This comes from frequent observation that
most people most of the time are not willing
to accept a fair gamble:
• Would you be willing to bet me $100 that you
can predict a coin flip?
– Most would say no.
– And if one of you says yes, I will say no, since I am
risk averse.
• Risk aversion implies concavity.
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
12

13. Expected utility of a prospect
• Consider prospect P7:
• P7(.4, 50,000, 1,000,000)
• Use expected utility formula:
U(P7) = 0.40u(50,000) + 0.60u(1,000,000)
• Using logarithmic utility function, we have:
U(P7) = 0.40(1.6094) + 0.60(4.6052) = 3.4069
• Graph also shows utility of exp. value of prospect:
u(E(w)) = ln(62) = 4.1271
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
13

14. Expected utility on graph
•
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
14

15. Certainty equivalents
• Certainty equivalent is defined as that wealth
level which leads decision-maker to be
indifferent between a particular prospect and
a certain wealth level.
• We need to solve for w below:
U(P7) = 3.4069 = u(w)
• Solution is w = 30.17
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
15

16. Problems with expected
utility theory
• A number of violations of expected utility
have been discovered.
• Most famous is Allais paradox.
• Alternative theories have been developed
which seek to account for these violations.
• Best-known is prospect theory of Daniel
Kahneman and Amos Tversky.
©2010 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or
posted to a publicly available website, in whole or in part.
16