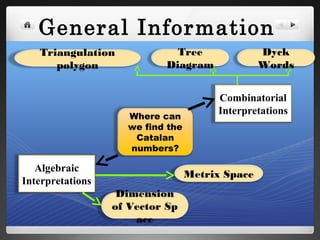
The document discusses Catalan numbers, which have various interpretations in combinatorics. Specifically: 1) Catalan numbers count the number of ways to triangulate a polygon with n+2 sides. 2) They also count the number of possible tree diagrams that can be drawn with n+1 leaves. 3) Additionally, Catalan numbers represent the number of arrangements of Dyck words of length 2n. The document provides historical background on Catalan numbers and explores proofs and interpretations of the numbers in fields like triangulation, trees, Dyck words, and monotonic paths on grids.

1. Catalan Numbers
and
Their Interpretations
Presented by
Pai Sukanya Suksak

2. What are the Catalan
Numbers?

3. Historical Information
In 1730 – Chinese
mathematician
Antu Ming
In 1751 – Swiss
mathematician
Leonhard Euler
In 1838 – Belgian
mathematician
Eugene Charles
Catalan

4. General Information
Where can
we find the
Catalan
numbers?
Combinatorial
Interpretations
Triangulation
polygon
Tree
Diagram
Dyck
Words
Algebraic
Interpretations
Dimension
of Vector Sp
ace
Metrix Space

5. The Catalan Numbers:
Sequence of Integer
Figure 1 The nth central binomial
coefficient of Pascal’s triangle which is
Let’s consider the numbers in circles
n = 0
n = 1
n = 2
n = 3
n = 4

6. Then, if we divide each central binomial
coefficient (1, 2, 6, 20, 70,…) by n + 1.
(i.e., 1, 2, 3, 4, 5,… respectively)
The first fifth terms: 1, 1, 2, 5, and 14
The first fifth terms of
the Catalan numbers
The Catalan Numbers:
Sequence of Integer

7. The Catalan Numbers:
The Formula
Theorem For any integer n ≥ 1, the Catalan
number Cn is given in term of binomial
coefficients by
For n ≥ 0

8. Proof by Triangulation Definition
The Catalan Numbers:
Proof of the Formula
Claim The formula of the Catalan numbers,
derives from Euler’s formula of triangulation
For n ≥ 0
Koshy first claim the triangulation formula of Euler which is
An = 2  6  10    (4n − 10) n
≥ 3 (n − 1)!

9. Proof by Triangulation Definition
The Catalan Numbers:
Proof of the Formula
Claim The formula of the Catalan numbers,
derives from Euler’s formula of triangulation
For n ≥ 0
An = 2  6  10    (4n − 10) n
≥ 3 (n − 1)!
By extending the formula to include the case n = 0, 1, and 2, and
rewriting the formula, Cn can be expressed as
Cn =
(4n − 2) n ≥ 1
(n − 1)! Cn-1
and C0 = 1

10. The Catalan Numbers:
Proof of the Formula
Cn = (4n − 2)
(n − 1)!
 Cn-1
To show the previously recursive formula is exactly
the formula of Catalan numbers, Koshy applies
algebraic processes as following.
(4n − 2)(4n – 6)(4n – 10) 
62 (n − 1)!
 C0
=
= 1
(n + 1) ( )2n
n
♯

11. The Catalan Numbers:
Some Interpretations
Judita Cofman draws the relationship among combinatorial
interpretations of the Catalan numbers as following.
1. The nth Catalan number is the number of
different ways to triangulate polygon with n + 2 sid
es.
Pentagon (n = 3), C3 = 5.
http://www.toulouse.ca/EdgeGuarding/MobileGuards.html

12. The Catalan Numbers:
Some Interpretations
Then, we are going to construct the tree-diagrams,
corresponding to the partitions.
2. The nth Catalan number is the number of
Different ways to construct tree-diagram with
n + 1 leave.
(Cofman, 1997)

13. The Catalan Numbers:
Some Interpretations
Then, we are going to label each branch of the tree-
diagram with r and l
(Cofman, 1997)

14. The Catalan Numbers:
Some Interpretations
The codes, derived from the labelled tree-diagrams, can
be formed the Dyck words of length 6
3. The nth Catalan number is the number of
different ways to arrange Dyck words of length 2n.
There are 5 different arrangements of
Dyck words of length 2n, where n = 3.
(Cofman, 1997)

15. The Catalan Numbers:
Some Interpretations
Let r stand for “moving right” and l stand for “going up”.
We will contruct monotonic paths in 3×3 square grid.
4. The nth Catalan number is the number of
different monotonic paths along n×n square grid.
(Cofman, 1997)

16. What is the Catalan
Numbers?

17. References
The Catalan Numbers
Conway, J., Guy, R. (1996). “THE BOOK OF NUMBERS”.
Copericus, New York.
Cofman, Judita (08/01/1997). "Catalan Numbers for the Classroom?".
Elemente der Mathematik (0013-6018), 52 (3), p. 108.
Koshy, T. (2007). “ELEMENTARY NUMBER THEORY WITH
APPLICATIONS”. Boston Academic Press, Massachusetts.
Stanley, R. (1944). “ENUMERATIVE COMBENATORICS”.
Wadsworth & Brooks/Cole Advanced Books & Software,
California.
Wikipedia, “Catalan Numbers”. Retrived November 3, 2010.

18. Thank you for your
attention