Tài liệu trình bày sự phát triển và các lý thuyết về liên kết hóa học, bao gồm các quan điểm nổi bật từ các nhà khoa học như Bergmann, Berzelius, Gerhardt, Dumas, Laurent, Kossel và Lewis. Các thuyết này đã giải thích và mô tả các quy luật và tính chất của cấu tạo phân tử, liên kết ion và cộng hóa trị từ cuối thế kỷ 18 đến giữa thế kỷ 20, cùng với sự phát triển của lý thuyết cơ học lượng tử về liên kết hóa học thông qua phương pháp Heitler-London. Cuối cùng, phương pháp VB được áp dụng để giải thích năng lượng và cấu trúc phân tử H2 dựa trên các hàm sóng và nguyên lý cơ bản của cơ học lượng tử.





![6
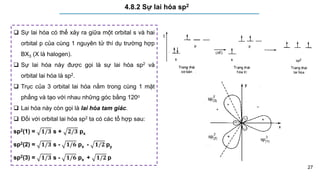
4.3 Các luận điểm cơ sở của Thuyết VB
Thuyết Heitler và London đã giải thích được bản chất “lực liên kết” cộng hóa trị và cũng chứng
minh được rằng không thể có sự kết hợp thêm 1 nguyên tử H thứ ba nào khác vào phân tử H2
nghĩa là đã giải thích được tính bão hòa về hóa trị.
Thuyết Heitler và London về phân tử H2 được phát triển và mở rộng thành thuyết VB áp dụng cho
phân tử nhiều nguyên tử. Theo thuyết VB, trong phân tử H2 có các cấu hình e của phân tử là:
(1sa)1(1sb)1 (Lưu ý: Heitler và London chỉ chú ý đến cấu hình này)
(1sa)2
(1sb)2
Trong thuyết VB, người ta gọi những hàm sóng đơn thu được từ các CH e là những cấu tạo hóa
trị. Xét phân tử H2 có các cấu tạo hóa trị sau: (dựa theo qui tắc nhân xác suất và nguyên lí không
phân biệt các hạt cùng loại).
Ψđồng cực = [Ψ1sa(1).Ψ1sb(2) + Ψ1sa(2).Ψ1sb(1)][α(1)β(2) - α(2)β(1)] ứng với CHe (1sa)1(1sb)1
Ψion = [Ψ1sa(1).Ψ1sa(2)[α(1)β(2) - α(2)β(1)] ứng với CHe (1sa)2
Ψion = [Ψ1sb(1).Ψ1sb(2)[α(1)β(2) - α(2)β(1)] ứng với CHe (1sb)2](https://image.slidesharecdn.com/c4-241002035554-30f65427/85/C4-Thuy-t-lien-k-t-hoa-tr-VB-pdf-6-320.jpg)




![11
4.4 Phương pháp Heitler – London giải bài toán H2
Hàm sóng mô tả trạng thái cơ bản của phân tử H2 là
hàm: Ψđc = [Ψa1 . Ψb2 + Ψb1 . Ψa2] [α(1)β(2) - α(2)β(1)]
Dựa trên các hàm sóng Ψ+ và Ψ-, Heitler và London đã
tính toán năng lượng các e trong phân tử H2 và xây
dựng đường cong thế năng. Kết quả thu được hai
đường cong có dạng giống với những đường cong thế
năng thực nghiệm (1) và (2): đường cong (1) tương
ứng hàm sóng đối xứng, đường cong (2) tương ứng
hàm sóng phản đối xứng.
Các giá trị ro và Eo của đường cong (1) theo tính toán
của Heitler và London bằng 0,869 Ao và 3,14 eV (gần
với giá trị thực nghiệm 0,741 Ao và 4,74 eV). Do vậy mà
pp Heitler và London được thừa nhận.](https://image.slidesharecdn.com/c4-241002035554-30f65427/85/C4-Thuy-t-lien-k-t-hoa-tr-VB-pdf-11-320.jpg)





















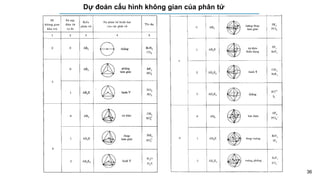
![34
Dự đoán trạng thái lai hóa của nguyên tử trung tâm
Bài tập áp dụng
Hãy dự đoán kiểu lai hóa trong các phân tử và ion sau:
a/ CO2 ; NH3 ; CCl4
b/ NH4
+; CO3
2-; [ICl4]-
a/ CO2
Số cặp e hóa trị tự do = (4 + 2 x 6) – 2 x 8 = 0
Số lk σ = 2
T = 0 + 2 = 2 lai hóa kiểu sp
NH3
Số cặp e hóa trị tự do = [(5 + 3 x 1) – 3 x 2]:2 = 1
Số lk σ = 3
T = 3 + 1 = 4 lai hóa kiểu sp3
CCl4
Số cặp e hóa trị tự do = [(4 + 7 x 4) – 8 x 4]:2 = 0
Số lk σ = 4
T = 0 + 4 = 4 lai hóa kiểu sp3
b/ NH4
+
Số cặp e hóa trị tự do = (5 + 4 x 1 -1) – 2 x 4 = 0
Số lk σ = 4
T = 4 + 0 = 4 lai hóa kiểu sp3
CO3
2-
Số cặp e hóa trị tự do = [(4 + 6 x 3 +2) – 3 x 8]:2 = 0
Số lk σ = 3
T = 3 + 0 = 3 lai hóa kiểu sp2
[ICl4]-
Số cặp e hóa trị tự do = [(7 + 7 x 4 + 1) – 8 x 4]:2 = 2
Số lk σ = 4
T = 2 + 4 = 6 lai hóa kiểu sp3d2](https://image.slidesharecdn.com/c4-241002035554-30f65427/85/C4-Thuy-t-lien-k-t-hoa-tr-VB-pdf-34-320.jpg)