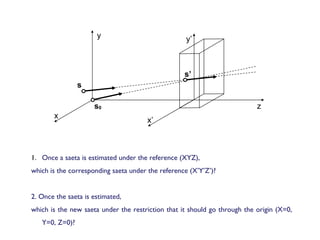
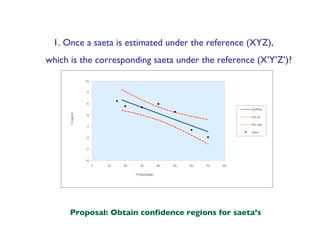
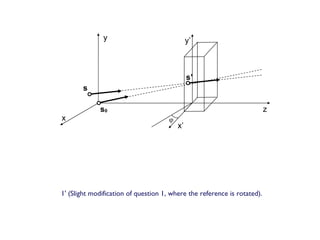
1. The document discusses methods for estimating and analyzing saetas (linear models). It proposes estimating a saeta under a new reference frame by applying the appropriate transformation to the estimated saeta coefficients. 2. Once a saeta is estimated, it can be restricted to pass through the origin by applying a linear restriction to the model estimation. The restriction can be tested with an F-test. 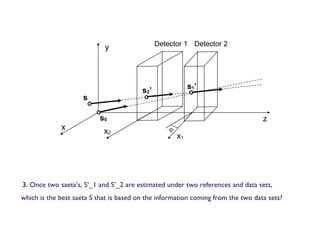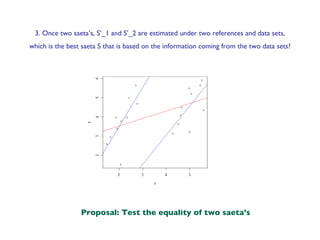3. When two saetas are estimated from different data sets, the best overall saeta can be determined by testing whether the two saetas are equal.

1. Reduction of saetas W.González-Manteiga and C. Sánchez-Sellero Department of Statistics and Operations Research University of Santiago de Compostela

2. Estimation of a saeta as a linear model The available data , denoted by Y, can be expressed as a function of known quantities, in the matrix X, unknow parameters, which determine the saeta, and some errors. It can be written in matrix form as a linear model: is assumed to be normal with mean zero and covariance matrix

3. Estimator and its properties The estimator can be obtained by which satisfies

4. Once a saeta is estimated under the reference (XYZ), which is the corresponding saeta under the reference (X’Y’Z’)? 2. Once the saeta is estimated, which is the new saeta under the restriction that it should go through the origin (X=0, Y=0, Z=0)? s s’ s 0 y x z x’ y’

5. 1. Once a saeta is estimated under the reference (XYZ), which is the corresponding saeta under the reference (X’Y’Z’)? Proposal: Obtain confidence regions for saeta’s

6. 2. Once the saeta is estimated, which is the new saeta under the restriction that it should go through the origin (X=0, Y=0, Z=0)? A linear model can be estimated under a linear restriction by In that case, and (assumption that it goes through the origin) can be tested by the F -test:

7. 3. Once two saeta’s, S’_1 and S’_2 are estimated under two references and data sets, which is the best saeta S that is based on the information coming from the two data sets? s s 1 ’ s 0 y x z φ s 2 ’ Detector 1 Detector 2 x 1 x 2

8. 3. Once two saeta’s, S’_1 and S’_2 are estimated under two references and data sets, which is the best saeta S that is based on the information coming from the two data sets? Proposal: Test the equality of two saeta’s

9. 1' (Slight modification of question 1, where the reference is rotated). s’ s s 0 y x z φ x’ y’