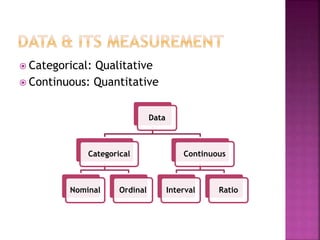
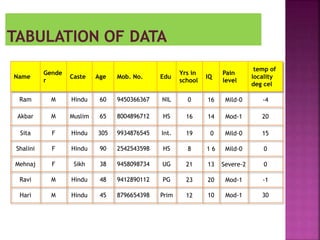
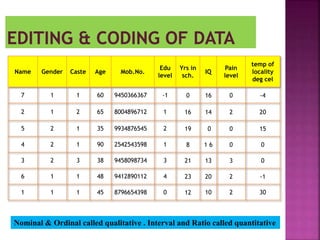
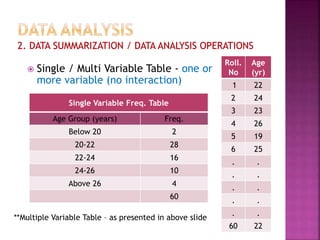
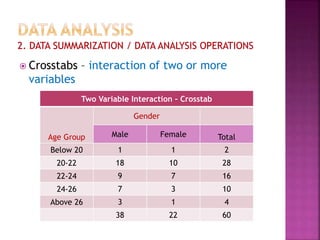
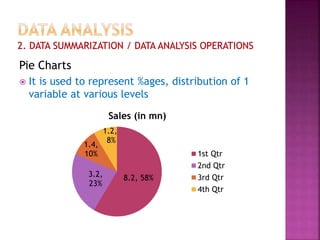
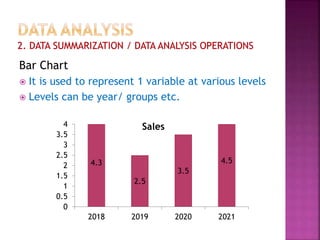
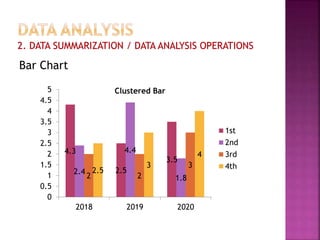
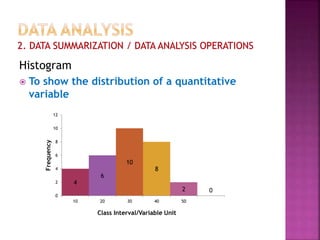
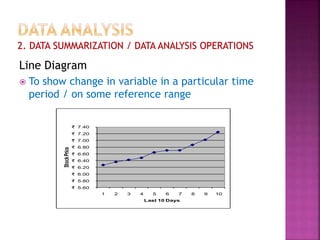
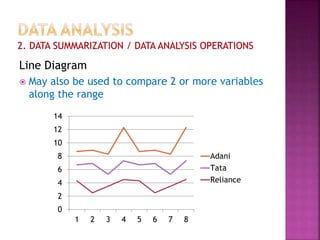
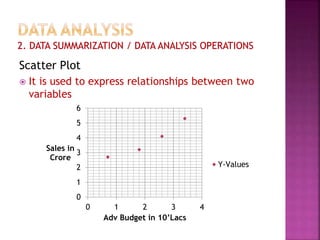
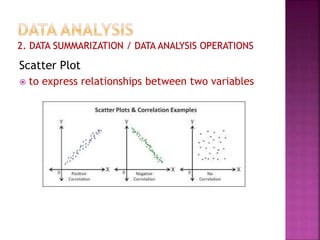
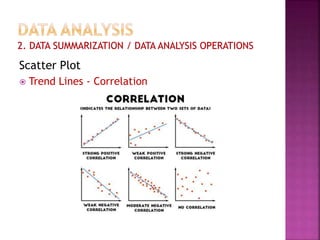
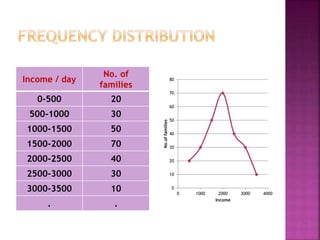
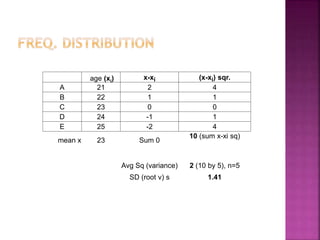
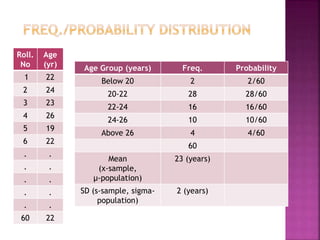
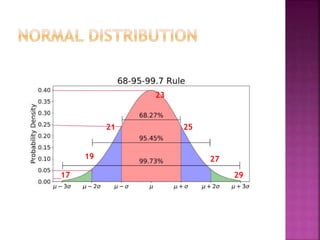
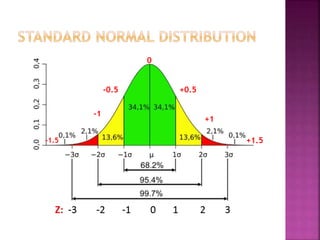
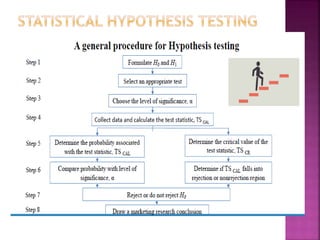
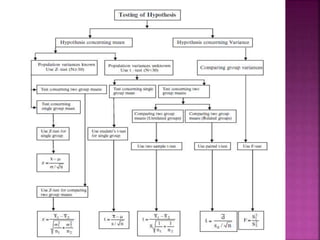
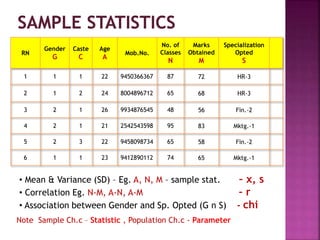
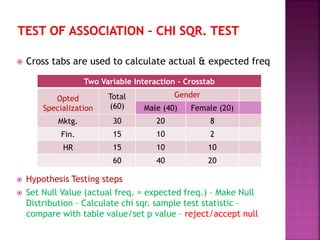
This document provides an overview of key concepts in data analysis and statistics. It defines different types of data (categorical, continuous) and variables (nominal, ordinal, interval, ratio). It then covers various steps in data analysis including data preparation, summarization, and descriptive and inferential statistical methods. Graphical representations like pie charts, bar graphs, histograms and scatter plots are also discussed. Hypothesis testing concepts like null/alternative hypotheses, p-values, and choosing test statistics based on data type are summarized.

1. Dr. Urooj A Siddiqui

2.  Data – Raw Facts, especially numerical facts,
collected together for reference or
information.
 Data is collected on some particular
variable/s
 Data analysis is processing of data to derive
useful information
 Knowledge communicated concerning some
particular fact
 The created knowledge helps in APPLICATION /
DECISION MAKING

3.  Categorical: Qualitative
 Continuous: Quantitative
Data
Categorical
Nominal Ordinal
Continuous
Interval Ratio

4.  Any phenomenon which takes at least two
different values/ observations
 Data: Set of values/ observations
collected on variable is called data
 Nominal
 Ordinal
 Interval
 Ratio

5. 1. Data Preparation / Initial
Operations
2. Summarizing Data / Data
Analysis Operations
 Editing / Cleaning
 Coding
 Classification
 Tabulation
 Graphical
Representation
 Tables / Crosstab
 Graph / Figure
 Statistical Analysis
1. Descriptive Methods
 Frequency, %age, Ratio,
 Mean, Median, Standard
Deviation (Variance)
2. Inferential Methods
 Comparison (t/z-test/Anova)
 Association (chi square test)
 Correlation (r)
 Prediction/ Regression
(y = ax + b)

6.  Editing / Data Cleaning
 examining the collected raw data to detect any errors
and omit/correct it if possible
 Coding
 assigning numerals to answers so that responses can
be put into a limited number of categories
 Classification
 Grouping of data on some basis (large volume of raw
data is reduced into homogenous groups
I. Attribute - on the basis of demographic bases
eg. gender, rural/urban, day scholar/hosteller
II. Class Interval – on the basis on some numeric range
eg. 0-10, 10-20 etc.

7. I. Tabulation
 is the process of displaying raw data in tabular
form and summarising it for further analysis
 orderly arranging data in columns and rows
Tabulation is essential because
 It conserves space and reduces statements
 It facilitates the process of summation of
items, comparison, detection of errors and
omissions
 Basis for various statistical computations

8. Name
Gende
r
Caste Age Mob. No. Edu
Yrs in
school
IQ
Pain
level
temp of
locality
deg cel
Ram M Hindu 60 9450366367 NIL 0 16 Mild-0 -4
Akbar M Muslim 65 8004896712 HS 16 14 Mod-1 20
Sita F Hindu 305 9934876545 Int. 19 0 Mild-0 15
Shalini F Hindu 90 2542543598 HS 8 1 6 Mild-0 0
Mehnaj F Sikh 38 9458098734 UG 21 13 Severe-2 0
Ravi M Hindu 48 9412890112 PG 23 20 Mod-1 -1
Hari M Hindu 45 8796654398 Prim 12 10 Mod-1 30

9. Name Gender Caste Age Mob.No.
Edu
level
Yrs in
sch.
IQ
Pain
level
temp of
locality
deg cel
7 1 1 60 9450366367 -1 0 16 0 -4
2 1 2 65 8004896712 1 16 14 2 20
5 2 1 35 9934876545 2 19 0 0 15
4 2 1 90 2542543598 1 8 1 6 0 0
3 2 3 38 9458098734 3 21 13 3 0
6 1 1 48 9412890112 4 23 20 2 -1
1 1 1 45 8796654398 0 12 10 2 30
Nominal & Ordinal called qualitative . Interval and Ratio called quantitative

10. Single Variable Freq. Table
Age Group (years) Freq.
Below 20 2
20-22 28
22-24 16
24-26 10
Above 26 4
60
Roll.
No
Age
(yr)
1 22
2 24
3 23
4 26
5 19
6 25
. .
. .
. .
. .
. .
60 22
 Single / Multi Variable Table - one or
more variable (no interaction)
**Multiple Variable Table – as presented in above slide

11.  Crosstabs – interaction of two or more
variables
Two Variable Interaction – Crosstab
Age Group
Gender
Male Female Total
Below 20 1 1 2
20-22 18 10 28
22-24 9 7 16
24-26 7 3 10
Above 26 3 1 4
38 22 60

12. Graphical Representation of Data
 Pie Chart
 Bar Graph
 Histogram
 Line Graph
 Scatter Plot
 Scatter Plot & Correlation

13. Pie Charts
 It is used to represent %ages, distribution of 1
variable at various levels
8.2, 58%
3.2,
23%
1.4,
10%
1.2,
8%
Sales (in mn)
1st Qtr
2nd Qtr
3rd Qtr
4th Qtr

14. Bar Chart
 It is used to represent 1 variable at various levels
 Levels can be year/ groups etc.
4.3
2.5
3.5
4.5
0
0.5
1
1.5
2
2.5
3
3.5
4
2018 2019 2020 2021
Sales

15. Bar Chart
4.3
2.5
3.5
2.4
4.4
1.8
2 2
3
2.5
3
4
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
2018 2019 2020
Clustered Bar
1st
2nd
3rd
4th

16. Histogram
 To show the distribution of a quantitative
variable
4
6
10
8
2 0
0
2
4
6
8
10
12
10 20 30 40 50
Frequency
Class Interval/Variable Unit

17. Line Diagram
 To show change in variable in a particular time
period / on some reference range
₹ 5.60
₹ 5.80
₹ 6.00
₹ 6.20
₹ 6.40
₹ 6.60
₹ 6.80
₹ 7.00
₹ 7.20
₹ 7.40
1 2 3 4 5 6 7 8 9 10
Stock
Price
Last 10 Days

18. Line Diagram
 May also be used to compare 2 or more variables
along the range
0
2
4
6
8
10
12
14
1 2 3 4 5 6 7 8
Adani
Tata
Reliance

19. Scatter Plot
 It is used to express relationships between two
variables
0
1
2
3
4
5
6
0 1 2 3 4
Sales in
Crore
Adv Budget in 10’Lacs
Y-Values

20. Scatter Plot
 to express relationships between two variables

21. Scatter Plot
 Trend Lines - Correlation

22. Income / day
No. of
families
0-500 20
500-1000 30
1000-1500 50
1500-2000 70
2000-2500 40
2500-3000 30
3000-3500 10
. .
0
10
20
30
40
50
60
70
80
0 1000 2000 3000 4000
No.of
families
Income

23. age (xi) x-xi (x-xi) sqr.
A 21 2 4
B 22 1 1
C 23 0 0
D 24 -1 1
E 25 -2 4
mean x 23 Sum 0
10 (sum x-xi sq)
Avg Sq (variance) 2 (10 by 5), n=5
SD (root v) s 1.41

24. Age Group (years) Freq. Probability
Below 20 2 2/60
20-22 28 28/60
22-24 16 16/60
24-26 10 10/60
Above 26 4 4/60
60
Mean
(x-sample,
µ-population)
23 (years)
SD (s-sample, sigma-
population)
2 (years)
Roll.
No
Age
(yr)
1 22
2 24
3 23
4 26
5 19
6 22
. .
. .
. .
. .
. .
60 22

25.  A distribution in frequencies of observations is
known – probability distribution
 Z- Normal Distribution/Test - Mean (µ), SD-
 To compare means (1 or 2 means)
 t – Distribution/Test- Mean (x), SD (s)
 To compare means (1 or 2 means)
 Chi Square Distribution / Test
 To compare sample SD with population SD
 F Test
 To compare two sample variances

26.  A freq. distribution with bell shape curve and
some known properties
 Parameters - Mean (µ), SD (sigma)
 Known properties
 68% values are within µ ± 1 SD
 95% values are within µ ± 2 SD
 99% values are within µ ± 3 SD
 95% CI = µ ± 2.SD (range)
 Lower limit µ - 2.SD
 Upper limit µ + 2.SD

27. 23
25
27
29
21
19
17

28. Example of our case
 95% CI = µ ± 2.SD
 Lower limit = µ - 2.SD, Upper limit = µ + 2.SD,
 LL = 23 - 2.2 = 19, UL = 23 + 2.2 = 27
 95% CI Range = 19-27 years
 95% of the students in the class are in the range
of 19-27 yrs
 We are 95% confident that if we randomly select
a student from the class his/her age will be
within this range (19-27 yrs)
 Reverse is Hypothesis Testing
 If mean and SD of any population is known and if
some value is given can we determine whether it
belongs to this population or distribution ?

29. 0
+0.5
+1
+1.5
-0.5
-1
-1.5

30. When Population SD is KNOWN When Population SD is UNKNOWN
Finding Probability
 Calculate z score (test statistic) of the observed
value or hypothesized value with the formula
 Determine p value associated with particular z
score at selected significance level (5%)
 P value can be seen in the tables of the particular
test
t =

32.  Two types of Hypothesis, Null - H0, Alternate - Ha

34. P Value Method
 Determine p value
 Compare with selected
alpha level (0.05)
 p ≤ 0.05 – Reject Null
 P > 0.05 – Fail to Reject
null / accept null
 This method is generally
employed by data analysis
software – Excel, SPSS
Table Value Method
 Calculate test statistic
value – Calculated TS
Value
 Determine Critical value
of test statistic at
selected significance level
– Table TS Value
 If TSCal ≥ TSTab – Reject
Null
 If TSCal < TSTab – Fail to
Reject null / accept null
 This method is generally
employed when manual
testing is done

38. RN
Gender
G
Caste
C
Age
A
Mob.No.
No. of
Classes
N
Marks
Obtained
M
Specialization
Opted
S
1 1 1 22 9450366367 87 72 HR-3
2 1 2 24 8004896712 65 68 HR-3
3 2 1 26 9934876545 48 56 Fin.-2
4 2 1 21 2542543598 95 83 Mktg.-1
5 2 3 22 9458098734 65 58 Fin.-2
6 1 1 23 9412890112 74 65 Mktg.-1
• Mean & Variance (SD) – Eg. A, N, M – sample stat. – x, s
• Correlation Eg. N-M, A-N, A-M – r
• Association between Gender and Sp. Opted (G n S) - chi
Note Sample Ch.c – Statistic , Population Ch.c - Parameter

39.  Assume a population – N, µ,
 Now assume we take many samples of size n and
calculate mean for each sample
 x1, x2, x3, x4, x5, x6, . . . . . . . . x100
 Can we make a freq. distribution of these values
and draw a curve?
 Now when we draw a distribution of these values
we will have an average (x) and SD (s)
 This average is called mean of means and
considered mean of population
 The SD of population is calculated as
which is called as Standard Error

42.  Sample mean & their difference - z / t
 Sample correlation statistic– z / t (derived from r)
 Variance (SD2) – F
 Association – Chi Sqr.
 Central Limit Theorem
 If we collect many samples and draw its
distribution the mean of this distribution is
population mean and SD of population is
 We use CLT in Hypothesis Testing

43.  z - when is Known and sample size is ≥ 30
 t - when is Unknown and sample size < 30
 In sample estimation t test is employed
 Example - H0 & H1
 H0 – There is no difference b/w mean of two groups
 H1 – There is a significant difference b/w mean of two groups
 H0 – There is no difference b/w mean marks of males &
females
 H1 – There is a significant difference b/w male & females
 Hypothesis Testing steps
 Set Null Value (u1=u2, u1-u2=0) – Make Null Distribution –
Calculate z /t sample test statistic – compare with table
value/set p value – reject/accept null

44.  Used to compare variance of two samples
 Employed in ANOVA – analysis of variance
 When there are more than two groups and their
means are to be compared
 Example
 Comparison of marks among three streams of
students arts, commerce and science
 H0 – There is no difference among mean marks of three groups
 H1 – There is a significant difference among mean marks of three
groups
 Set Null Value (µ1=µ2=µ3) – Make Null Distribution – Calculate F
test statistic – compare with table value/p value – reject/accept
null

45.  Test of Independence
 It is used to determine association between two
categorical variables (nominal & ordinal)
 Example
 Gender (M/F) and Opted Specialization (M/F/HR)
 Question like ‘is any specialisation is preferred by
females?’ are answered
 H0 – There is no association b/w gender and opted speclisa.n
 H1 – There is a significant association b/w gender & opted
speclisa.n
 Here, mean is not calculated instead frequency of categories
is taken into consideration
 Actual Frequency and Expected Frequency

46.  Cross tabs are used to calculate actual & expected freq
 Hypothesis Testing steps
 Set Null Value (actual freq. = expected freq.) – Make Null
Distribution – Calculate chi sqr. sample test statistic –
compare with table value/set p value – reject/accept null
Two Variable Interaction – Crosstab
Opted
Specialization
Total
(60)
Gender
Male (40) Female (20)
Mktg. 30 20 8
Fin. 15 10 2
HR 15 10 10
60 40 20

47.  Set Null and Alternate Hypothesis – H0 H1
 Select the null value
 Null – status quo, no difference, no effect
 Status quo – no change
 No difference – 0 difference
 No relationship – 0 effect / 0 correlation
 No association – 0 relationship (b/w nominal variab.)
 It is assumed that H0 is true in population
 Draw Null Distribution – find range of expected values
if null is true (µ ± 2.SE)
 Take observed value from sample and compare with
expected null values
 If observed value is among expected null range –
accept null
 If observed value is different from null range – reject
null

48. 1. Univariate/Bi-variate 2. Muti-variate
 Mean/Variance
Estimation
 Z test
 T test
 Chi Square
 F Test
 Correlation
 Correlation
 Regression
 Discriminant
 Cluster Analysis etc.

49.  Regression analysis
 1 dependent variable/DV (continuous)
 many independent variables/IV (continuous)
 Y = a.x1 +b.x2 +c.x3…….+.x.n
 Discriminant analysis
 1 dependent variable (catgorical)
 many independent variables (continuous)
 Z (yes/no) = a.x1 +b.x2 +c.x3…….+.x.n

50.  Cluster analysis
 No DV/IV
 Used to group respondents/customers in
various cluster
 Employed in market segmentation
 Factor analysis
 No DV/IV
 Used to group variables in various cluster of
more condensed variables