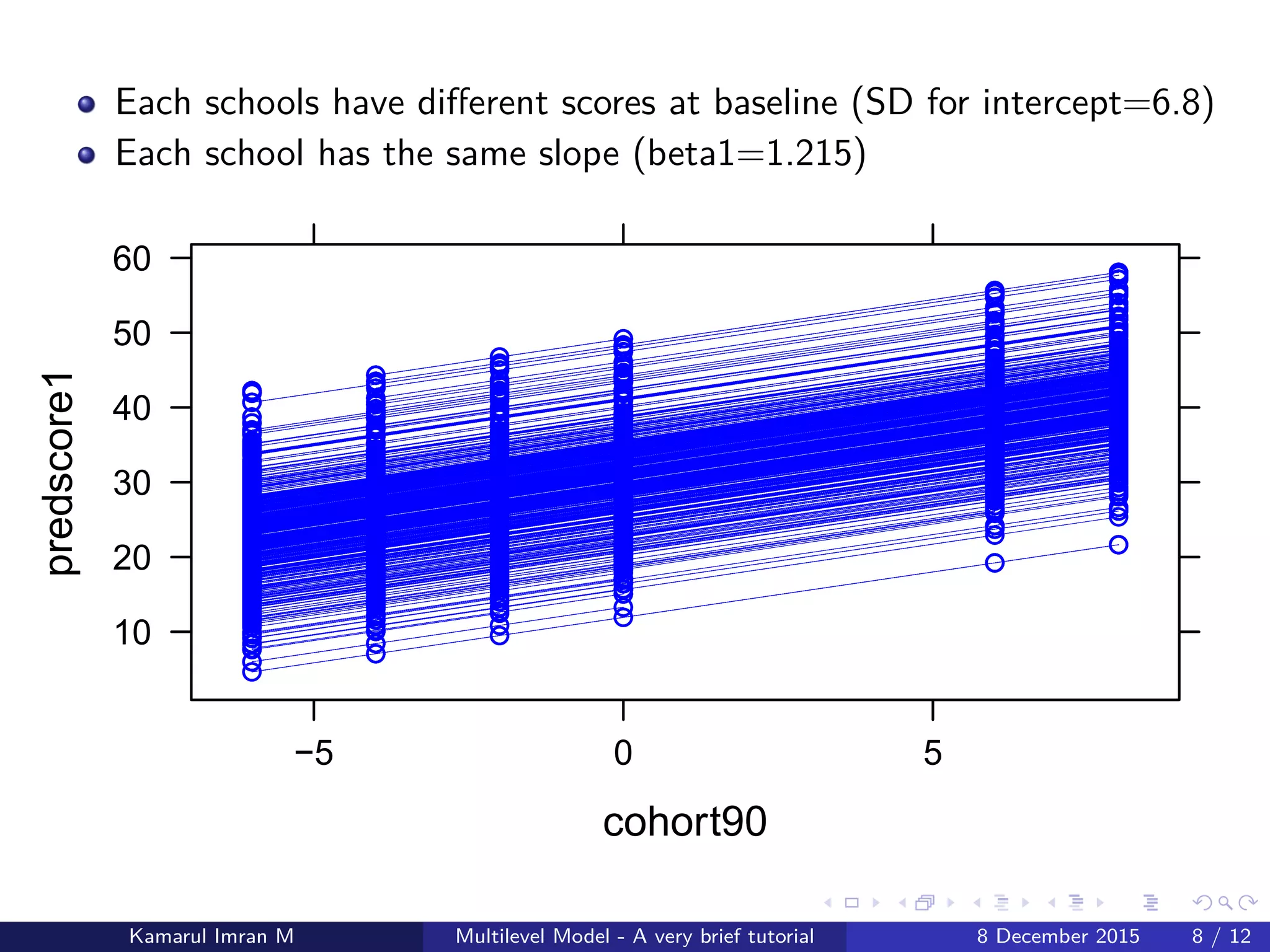
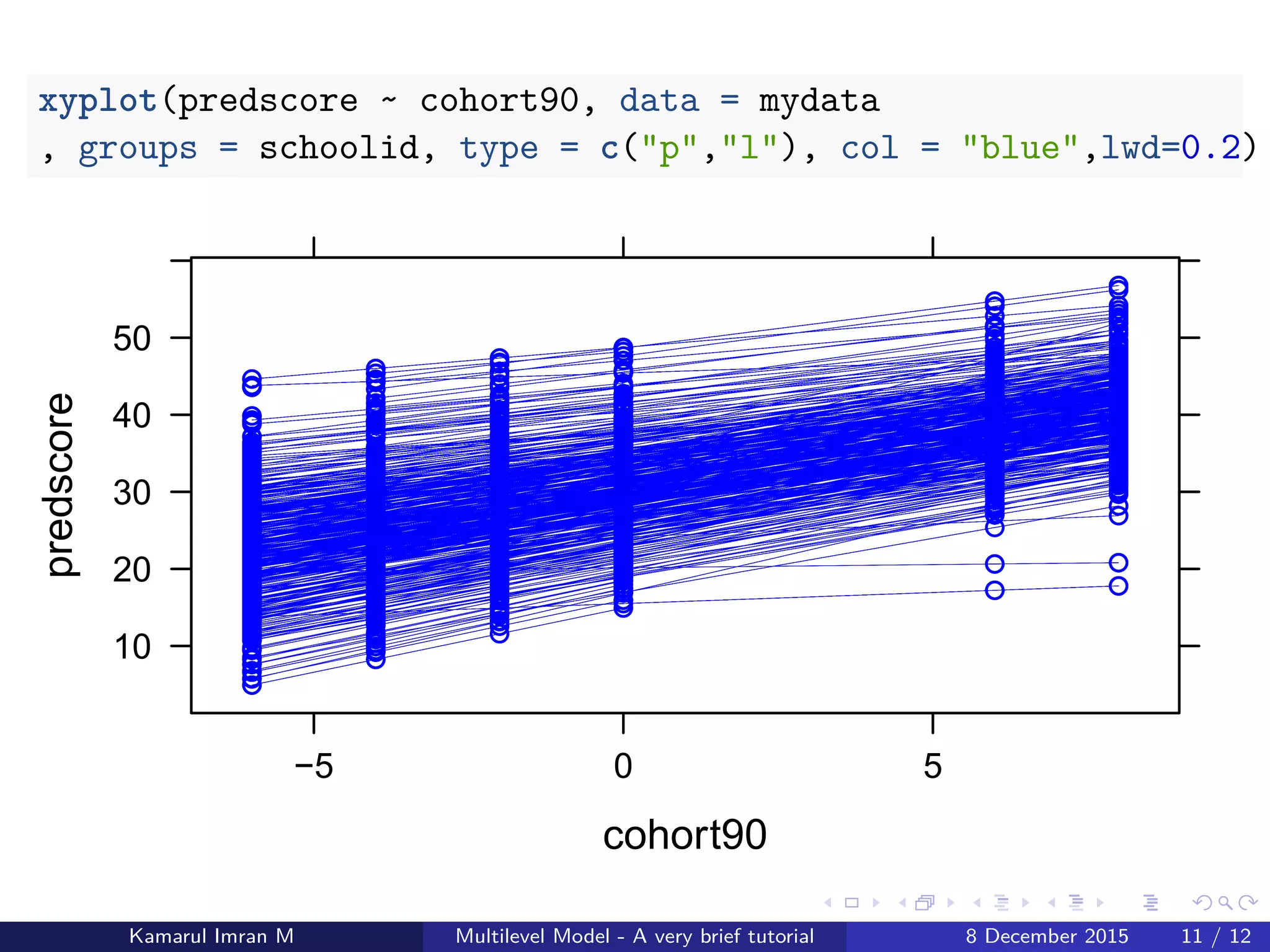
This document provides a brief tutorial on multilevel modeling, focusing on the analysis of data collected from pupils in schools across different hierarchical levels. It explains how to set up and analyze data using linear mixed models, including random intercept and random slope models, to account for variations within and between groups. The findings indicate that multilevel models offer more accurate insights compared to traditional linear regression methods.

1. Multilevel Model - A very brief tutorial
Kamarul Imran M
8 December 2015
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 1 / 12

2. Motivation
You may collect data from groups
These groups may be selected from different levels or hierarchy
The elements of members in a particular group share more similar
features or characteristics.
For example
Level 3 districts
Level 2 schools (school)
Level 1 pupils (case)
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 2 / 12

3. Our data
caseid - pupils in school - Level 1
schoolid - schools where pupils belong - Level 2
setwd("/Volumes/DATA/RandSpatialAndArcGISNotes/MixedModels")
mydata <- read.table("5.1.txt", sep = ",", header = TRUE)
summary(mydata)[, c(1, 2)]
## caseid schoolid
## "Min. : 1 " "Min. : 1.0 "
## "1st Qu.: 8532 " "1st Qu.:123.0 "
## "Median :17318 " "Median :256.0 "
## "Mean :18466 " "Mean :254.4 "
## "3rd Qu.:29428 " "3rd Qu.:386.0 "
## "Max. :38192 " "Max. :511.0 "
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 3 / 12

4. Variables
Dependent variable is score
Covariate is cohort90 (different cohorts of pupils in schools)
summary(mydata)[,c(3,4)]
## score cohort90
## "Min. : 0.00 " "Min. :-6.0000 "
## "1st Qu.:19.00 " "1st Qu.:-4.0000 "
## "Median :33.00 " "Median :-2.0000 "
## "Mean :31.09 " "Mean : 0.2767 "
## "3rd Qu.:45.00 " "3rd Qu.: 6.0000 "
## "Max. :75.00 " "Max. : 8.0000 "
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 4 / 12

5. Dataframe
A glimpse of our data
head(mydata,4)[,1:4]
## caseid schoolid score cohort90
## 1 18 1 0 -6
## 2 17 1 10 -6
## 3 19 1 0 -6
## 4 20 1 40 -6
tail(mydata,4)[,1:4]
## caseid schoolid score cohort90
## 33985 6493 511 20 -6
## 33986 6496 511 48 -6
## 33987 6494 511 10 -6
## 33988 6495 511 0 -6
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 5 / 12

6. Random intercept (RI) model
we will fit an RI model using a linear mixed model
model with only 1 covariate (for simplicity) - cohort90
## Loading required package: Matrix
ri1<-lmer(score~cohort90+(1|schoolid),data=mydata,REML=FALSE)
fixef(ri1)
## (Intercept) cohort90
## 30.559151 1.214955
VarCorr(ri1)
## Groups Name Std.Dev.
## schoolid (Intercept) 6.7815
## Residual 14.8084
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 6 / 12

7. The RI results
On average, the score at baseline was 30.6
On average, with 1 unit increase in cohort, the score increases for 1.22
We will see the plot.
The y axis is the score (dependent)
The x axis is the cohort (covariate=beta1)
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 7 / 12

8. Each schools have different scores at baseline (SD for intercept=6.8)
Each school has the same slope (beta1=1.215)
cohort90
predscore1
10
20
30
40
50
60
−5 0 5
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 8 / 12

9. Random slope (RS) model
Each schools have different score at baseline (SD for intercept=6.5)
Each school has the different slope (SD for beta1=0.40)
rs1 <- lmer(score ~ cohort90 + (1 + cohort90 | schoolid),
data = mydata, REML = FALSE)
fixef(rs1)
## (Intercept) cohort90
## 30.609633 1.233903
VarCorr(rs1)
## Groups Name Std.Dev. Corr
## schoolid (Intercept) 6.54660
## cohort90 0.40074 -0.390
## Residual 14.68807
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 9 / 12

10. Intercept and slope correlation
The average score for schools at baseline = 30.6 (SD=6.5)
The average slope for schools with 1 unit increase in cohort = 1.233
(SD=0.39)
The intercept-slope correlation = -0.390
Negative correlation means
Schools with lower baseline score have higher slope
Schools with higher baseline score have lower slope
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 10 / 12

11. xyplot(predscore ~ cohort90, data = mydata
, groups = schoolid, type = c("p","l"), col = "blue",lwd=0.2)
cohort90
predscore
10
20
30
40
50
−5 0 5
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 11 / 12

12. Summary
Multilevel data needs special treatment
Random variations between members in different levels
variations at baseline
variations for slope
Linear mixed model provides more useful information than linear
regression
Linear mixed model more accurately reflects our data than linear
regression
THANKS
Kamarul Imran M Multilevel Model - A very brief tutorial 8 December 2015 12 / 12