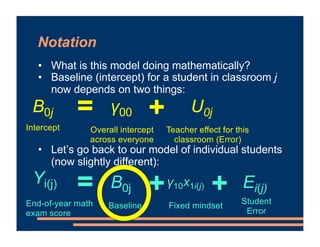
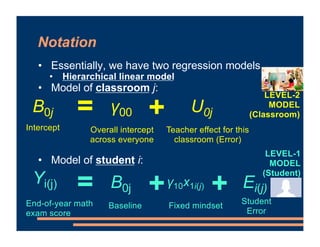
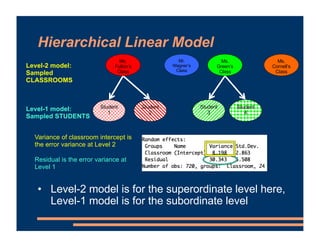
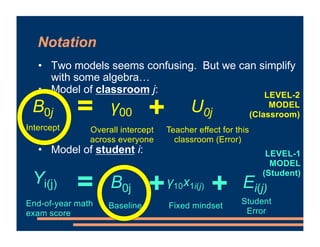
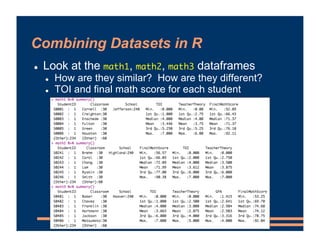
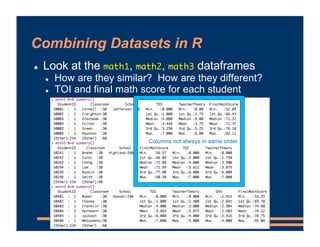
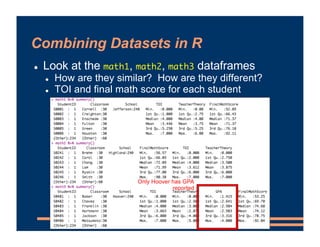
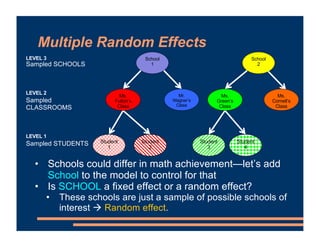
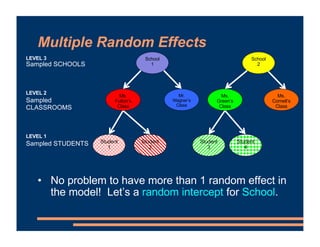
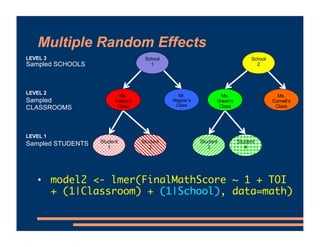
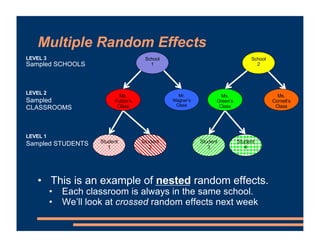
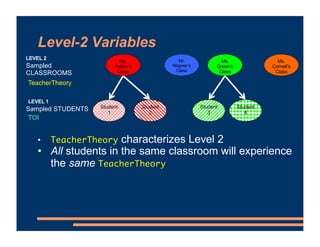
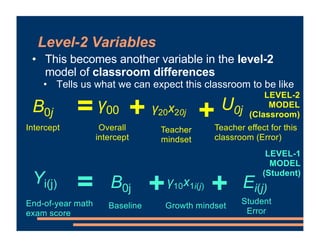
This document discusses including level-2 variables in multilevel models. It explains that level-2 variables characterize groups (like classrooms) and are invariant within groups. An example adds the variable "TeacherTheory" to characterize teachers' mindset and explain differences between classrooms. This reduces unexplained classroom variance but does not change the level-1 model or residuals. Cross-level interactions like the effect of a student's mindset depending on their teacher's mindset can also be added. Including level-2 variables provides more information about group differences but does not alter the basic multilevel structure.

1. Week 5.1: Level-2 Variables
! Notation
! Multiple Random Effects
! Combining Datasets in R
! Modeling
! Level-2 Variables
! Including Level-2 Variables in R
! Modeling Consequences
! Cross-Level Interactions
! Lab

2. Recap
• Last week, we created a model of middle
schoolers’ math performance that included a
random intercept for Classroom
• model1 <- lmer(FinalMathScore ~ 1 + TOI +
(1|Classroom), data=math)
Fixed effect of
naive theory
of intelligence
Average
intercept
(averaged all
classrooms)
Variance in
that intercept
from one class
to the next
Residual
(unexplained)
variance at
the child level

3. Notation
• What is this model doing mathematically?
• Let’s go back to our model of individual students
(now slightly different):
Student
Error
Ei(j)
=
End-of-year math
exam score
+ +
Baseline
Yi(j) B0j
Fixed mindset
γ10x1i(j)

4. Notation
• What is this model doing mathematically?
• Let’s go back to our model of individual students
(now slightly different):
Student
Error
Ei(j)
=
End-of-year math
exam score
+ +
Baseline
Yi(j) B0j
Fixed mindset
γ10x1i(j)
What now determines the baseline that
we should expect for students with
fixed mindset=0?

5. Notation
• What is this model doing mathematically?
• Baseline (intercept) for a student in classroom j
now depends on two things:
• Let’s go back to our model of individual students
(now slightly different):
Student
Error
Ei(j)
=
End-of-year math
exam score
+ +
Baseline
Yi(j) B0j
Fixed mindset
γ10x1i(j)
U0j
=
Intercept
+
Overall intercept
across everyone
B0j γ00
Teacher effect for this
classroom (Error)

6. Notation
• Essentially, we have two regression models
• Hierarchical linear model
• Model of classroom j:
• Model of student i:
Student
Error
Ei(j)
=
End-of-year math
exam score
+ +
Baseline
Yi(j) B0j
Fixed mindset
γ10x1i(j)
U0j
=
Intercept
+
B0j γ00
Teacher effect for this
classroom (Error)
LEVEL-1
MODEL
(Student)
LEVEL-2
MODEL
(Classroom)
Overall intercept
across everyone

7. Hierarchical Linear Model
Student
1
Student
2
Student
3
Student
4
Level-1 model:
Sampled STUDENTS
Mr.
Wagner’s
Class
Ms.
Fulton’s
Class
Ms.
Green’s
Class
Ms.
Cornell’s
Class
Level-2 model:
Sampled
CLASSROOMS
• Level-2 model is for the superordinate level here,
Level-1 model is for the subordinate level
Variance of classroom intercept is
the error variance at Level 2
Residual is the error variance at
Level 1

8. Notation
• Two models seems confusing. But we can simplify
with some algebra…
• Model of classroom j:
• Model of student i:
Student
Error
Ei(j)
=
End-of-year math
exam score
+ +
Baseline
Yi(j) B0j
Fixed mindset
γ10x1i(j)
U0j
=
Intercept
+
B0j γ00
Teacher effect for this
classroom (Error)
LEVEL-1
MODEL
(Student)
LEVEL-2
MODEL
(Classroom)
Overall intercept
across everyone

9. Notation
• Substitution gives us a single model that combines
level-1 and level-2
• Mixed effects model
• Combined model:
Student
Error
Ei(j)
=
End-of-year math
exam score
+ +
Yi(j)
Fixed mindset
γ10x1i(j)
U0j
+
Overall
intercept
γ00
Teacher effect for this
classroom (Error)

10. Notation
• Just two slightly different ways of writing the same
thing. Notation difference, not statistical!
• Mixed effects model:
• Hierarchical linear model:
Ei(j)
= + +
Yi(j)
γ10x1i(j)
U0j
+
γ00
Ei(j)
=
Yi(j) B0j
γ10x1i(j)
U0j
= +
B0j γ00
+ +

11. Notation
• lme4 always uses the mixed-effects model notation
• lmer(
FinalMathScore ~ 1 + TOI + (1|Classroom)
)
• (Level-1 error is always implied, don’t have to
include)
Student
Error
Ei(j)
=
End-of-year math
exam score
+ +
Yi(j)
Fixed mindset
γ10x1i(j) U0j
+
Overall
intercept
γ00
Teacher
effect
for this
class (Error)

12. Week 5.1: Level-2 Variables
! Notation
! Multiple Random Effects
! Combining Datasets in R
! Modeling
! Level-2 Variables
! Including Level-2 Variables in R
! Modeling Consequences
! Cross-Level Interactions
! Lab

13. ! We’re continuing our study of naïve theories of
intelligence & math performance
! We’ve now collected data at three different
schools
! math1.csv from Jefferson Middle School
! math2.csv from Highland Middle School
! math3.csv from Hoover Middle School
Combining Datasets in R

14. Combining Datasets in R
! Look at the math1, math2, math3 dataframes
! How are they similar? How are they different?
! TOI and final math score for each student

15. Combining Datasets in R
! Look at the math1, math2, math3 dataframes
! How are they similar? How are they different?
! TOI and final math score for each student
Columns not always in same order

16. Combining Datasets in R
! Look at the math1, math2, math3 dataframes
! How are they similar? How are they different?
! TOI and final math score for each student
Only Hoover has GPA
reported

17. Combining Datasets in R
! Overall, this is similar information, so let’s
combine it all
! Paste together the rows from two (or more)
dataframes to create a new one:
! bind_rows(math1, math2, math3) -> math
! Useful when observations are spread across files
! Or, to create a dataframe that combines 2 filtered
dataframes
math1
math2
math3
math

18. bind_rows(): Results
! Resulting dataframe:
! nrow(math) is 720 – all three combined
math1
math2
math3
math

19. ! Resulting dataframe:
! bind_rows() is smart!
! Not a problem that column order varies across
dataframes
! Looks at the column names
! Not a problem that GPA column only existed in one of
the original dataframes
! NA (missing data) for the students at the other schools
bind_rows(): Results

20. bind_rows(): Results
! Resulting dataframe:
! You can also add the optional .id argument
! bind_rows(math1, math2, math3,
.id='OriginalDataframe’) -> math
! Adds another column that tracks which of the original
dataframes (by number) each observation came from

21. Other, Similar Functions
! bind_rows() pastes together every row from
every dataframe, even if there are duplicates
! If you want to skip duplicates, use union()
! Same syntax as bind_rows(), just different function name
! Other related functions:
! intersect(): Keep only the rows that appear in all of
the source dataframes
! setdiff(): Keep only the rows that appear in a single
source dataframe—if duplicates, delete both copies

22. Week 5.1: Level-2 Variables
! Notation
! Multiple Random Effects
! Combining Datasets in R
! Modeling
! Level-2 Variables
! Including Level-2 Variables in R
! Modeling Consequences
! Cross-Level Interactions
! Lab

23. Multiple Random Effects
• Schools could differ in math achievement—let’s add
School to the model to control for that
• Is SCHOOL a fixed effect or a random effect?
• These schools are just a sample of possible schools of
interest " Random effect.
School
1
School
2
Sampled SCHOOLS
Sampled
CLASSROOMS
Sampled STUDENTS
LEVEL 3
LEVEL 2
LEVEL 1
Student
1
Student
2
Student
3
Student
4
Mr.
Wagner’s
Class
Ms.
Fulton’s
Class
Ms.
Green’s
Class
Ms.
Cornell’s
Class

24. Multiple Random Effects
• No problem to have more than 1 random effect in
the model! Let’s a random intercept for School.
School
1
School
2
Sampled SCHOOLS
Sampled
CLASSROOMS
Sampled STUDENTS
LEVEL 3
LEVEL 2
LEVEL 1
Student
1
Student
2
Student
3
Student
4
Mr.
Wagner’s
Class
Ms.
Fulton’s
Class
Ms.
Green’s
Class
Ms.
Cornell’s
Class

25. Multiple Random Effects
• model2 <- lmer(FinalMathScore ~ 1 + TOI
+ (1|Classroom) + (1|School), data=math)
School
1
School
2
Sampled SCHOOLS
Sampled
CLASSROOMS
Sampled STUDENTS
LEVEL 3
LEVEL 2
LEVEL 1
Student
1
Student
2
Student
3
Student
4
Mr.
Wagner’s
Class
Ms.
Fulton’s
Class
Ms.
Green’s
Class
Ms.
Cornell’s
Class

26. Multiple Random Effects
• model2 <- lmer(FinalMathScore ~ 1 + TOI
+ (1|Classroom) + (1|School), data=math)
• Less variability across schools than classrooms in a school

27. Multiple Random Effects
• This is an example of nested random effects.
• Each classroom is always in the same school.
• We’ll look at crossed random effects next week
School
1
School
2
Sampled SCHOOLS
Sampled
CLASSROOMS
Sampled STUDENTS
LEVEL 3
LEVEL 2
LEVEL 1
Student
1
Student
2
Student
3
Student
4
Mr.
Wagner’s
Class
Ms.
Fulton’s
Class
Ms.
Green’s
Class
Ms.
Cornell’s
Class

28. Week 5.1: Level-2 Variables
! Notation
! Multiple Random Effects
! Combining Datasets in R
! Modeling
! Level-2 Variables
! Including Level-2 Variables in R
! Modeling Consequences
! Cross-Level Interactions
! Lab

29. Level-2 Variables
• So far, all our model says about classrooms is
that they’re different
• Some classrooms have a large intercept
• Some classrooms have a small intercept
• But, we might also have some interesting
variables that characterize classrooms
• They might even be our main research interest!
• How about teacher theories of intelligence?
• Might affect how they interact with & teach students

30. Level-2 Variables
Student
1
Student
2
Student
3
Student
4
Sampled STUDENTS
Mr.
Wagner’s
Class
Ms.
Fulton’s
Class
Ms.
Green’s
Class
Ms.
Cornell’s
Class
Sampled
CLASSROOMS
• TeacherTheory characterizes Level 2
• All students in the same classroom will experience
the same TeacherTheory
LEVEL 2
LEVEL 1
TeacherTheory
TOI

31. Level-2 Variables
• Is TeacherTheory a fixed effect or random
effect?
• Teacher mindset is a fixed-effect variable
• We ARE interested in the effects of teacher mindset
on student math achievement … a research
question, not just something to control for
• Even if we ran this with a new random sample of 30
teachers, we WOULD hope to replicate whatever
regression slope for teacher mindset we observe
(whereas we wouldn’t get the same 30 teachers
back)

32. Level-2 Variables
• This becomes another variable in the level-2
model of classroom differences
• Tells us what we can expect this classroom to be like
Student
Error
Ei(j)
=
End-of-year math
exam score
+ +
Baseline
Yi(j) B0j
Growth mindset
γ10x1i(j)
U0j
=
Intercept
+
Overall
intercept
B0j
γ00
Teacher effect for this
classroom (Error)
LEVEL-1
MODEL
(Student)
LEVEL-2
MODEL
(Classroom)
Teacher
mindset
+
γ20x20j

33. Level-2 Variables
• Since R uses mixed effects notation, we don’t
have to do anything special to add a level-2
variable to the model
• model3 <- lmer(FinalMathScore ~ 1 + TOI
+ TeacherTheory + (1|Classroom) +
(1|School), data=math)
• R automatically figures out TeacherTheory is a
level-2 variable because it’s invariant for each
classroom
• We keep the random intercept for Classroom
because we don’t expect TeacherTheory will
explain all of the classroom differences. Intercept
captures residual differences.

34. Week 5.1: Level-2 Variables
! Notation
! Multiple Random Effects
! Combining Datasets in R
! Modeling
! Level-2 Variables
! Including Level-2 Variables in R
! Modeling Consequences
! Cross-Level Interactions
! Lab

35. What Changes? What Doesn’t?
• Random classroom & school variance is reduced.
• Teacher theories of intelligence accounts for some of the variance
among classrooms (and among the schools those classrooms are in).
• TeacherTheory explains some of the “Class j” effect we’re substituting
into the level 1 equation. No longer just a random intercept.
WITHOUT TEACHERTHEORY WITH TEACHERTHEORY

36. What Changes? What Doesn’t?
• Residual error at level 1 essentially unchanged.
• Describes how students vary from the class average
• Divergence from the class average cannot be explained by teacher
• Regardless of what explains the “Class j” effect, you’re still substituting it
into the same Lv 1 model
WITHOUT TEACHERTHEORY WITH TEACHERTHEORY

37. What Changes? What Doesn’t?
• Similarly, our level-1 fixed effect is essentially unchanged
• Explaining where level-2 variation comes from does not change our
level-1 model
• Note that average student TOI and TeacherTheory are very slightly
correlated (due to random chance); otherwise, there’d be no change.
WITHOUT TEACHERTHEORY WITH TEACHERTHEORY

38. Week 5.1: Level-2 Variables
! Notation
! Multiple Random Effects
! Combining Datasets in R
! Modeling
! Level-2 Variables
! Including Level-2 Variables in R
! Modeling Consequences
! Cross-Level Interactions
! Lab

39. Cross-Level Interactions
• Because R uses mixed effects notation, it’s also
very easy to add interactions between level-1
and level-2 variables
• model4 <- lmer(FinalMathScore ~ 1 + TOI
+ TeacherTheory + TOI:TeacherTheory +
(1|Classroom) + (1|School), data=math)
• Does the effect of a student’s theory of intelligence
depend on what the teacher’s theory is?
• e.g., maybe matching theories is beneficial

40. Cross-Level Interactions
• Because R uses mixed effects notation, it’s also
very easy to add interactions between level-1
and level-2 variables
• In this case, the interaction is not significant

41. Week 5.1: Level-2 Variables
! Notation
! Multiple Random Effects
! Combining Datasets in R
! Modeling
! Level-2 Variables
! Including Level-2 Variables in R
! Modeling Consequences
! Cross-Level Interactions
! Lab