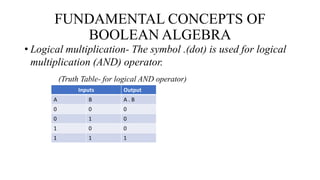
Boolean algebra uses the values true (1) and false (0) for variables. It defines three main operations: AND (.); OR (+); and NOT (¬). Boolean algebra was introduced by George Boole and is useful for designing computer logic circuits. It has fundamental concepts like logical addition, multiplication, and complementation defined by truth tables. Boolean algebra also defines postulates like identity, commutative, associative, distributive laws and the principle of duality.

1. Boolean Algebra
UNIT-II

2. BOOLEAN ALGEBRA
• Boolean algebra is the branch of algebra in which the values
of the variables are the truth values true and false, usually
denoted 1 and 0, respectively.
• The main operations of Boolean algebra are the AND
operation denoted as ., the OR operation denoted as +, and
the NOT operation denoted as ¬.
• Boolean algebra was introduced by George Boole .
• It is very useful in designing logic circuits used in processors
of computer systems.

3. FUNDAMENTAL CONCEPTS OF
BOOLEAN ALGEBRA
• Boolean algebra deals with 0 and 1.
• The variables in Boolean expressions like A+B=C where
variables A,B,C can have only two possible values- 0 and 1.
• Logical addition- The symbol + is used for logical addition
(OR) operator.
(Truth Table- for logical or operator)
Inputs Output
A B A+B=C
0 0 0
0 1 1
1 0 1
1 1 1
The truth table gives resulting output
values for each of the four input
combinations. S

4. FUNDAMENTAL CONCEPTS OF
BOOLEAN ALGEBRA
• Logical multiplication- The symbol .(dot) is used for logical
multiplication (AND) operator.
(Truth Table- for logical AND operator)
Inputs Output
A B A . B
0 0 0
0 1 0
1 0 0
1 1 1

5. FUNDAMENTAL CONCEPTS OF
BOOLEAN ALGEBRA
• Complementation- Complementation is a unary operation
defined on a single variable. The symbol ¬ is used for NOT
operator.
(Truth Table- for logical NOT operator)
Input Output
A ¬A =~A=𝐴
0 1
1 0

6. FUNDAMENTAL CONCEPTS OF
BOOLEAN ALGEBRA
• Operator precedence
A+B . C can have different values if the expression is (A+B).C
and A+ (B.C)
The precedence rules for Boolean operators are as follows.
1. The expression is scanned from left to right.
2. Expression enclosed within parenthesis are evaluated first.
3. All NOT operators are evaluated first
4. All AND operations are evaluated after that
5. Finally + or OR operations are performed in the end.

7. POSTULATES OF BOOLEAN ALGEBRA
• Postulate or axiom 1
a) A=0, if and only if , A ≠1.
b) A=1, if and only if, A ≠0.
• Postulate 2(Identity law)
a) A+0=A
b) A.1=A
• Postulate 3: Commutative law
a)A+B= B+A
b)A.B=B.A

8. POSTULATES OF BOOLEAN ALGEBRA
• Postulate 4:Associative law
a) A+(B+C)=(A+B)+C
b) A.(B.C)=(A.B).C
• Postulate 5:Distributive law
a) A.(B+C)=A.B+A.C
b) A+(B.C)=(A+B).(A+C)
• Postulate 6 (Complement)
a)A+ 𝐴 =1
b)A .𝐴 =0

9. PRINCIPLE OF DUALITY
• In Boolean algebra there is precise duality between operators
AND and OR , and the values of Boolean variables 0 and 1 .
• The principle of duality states that if we prove a Boolean
statement is a valid one, then its dual is also valid.
• ‘1+1=1’is Boolean statement which a valid one . Then by
interchanging the 1 with 0 and + with . , we get the dual of this
Boolean statement ‘0.0=0’which is also a valid one.
To get the dual of a Boolean statement, we interchange 1 with 0
and 0 with 1. Also + with . , and . with +.