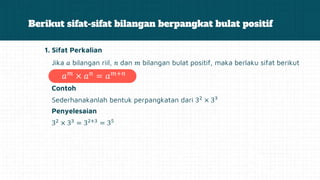
Dokumen ini menjelaskan tentang fungsi eksponensial dengan bilangan berpangkat positif, termasuk definisi, sifat-sifat, dan contoh perhitungan. Terdapat berbagai sifat seperti sifat perkalian, pembagian, dan pangkat, serta cara menyederhanakan perpangkatan. Banyak diberikan contoh untuk membantu pemahaman tentang cara menghitung dan menerapkan konsep pangkat dalam bilangan.