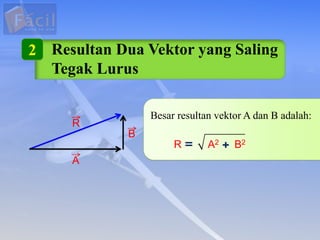
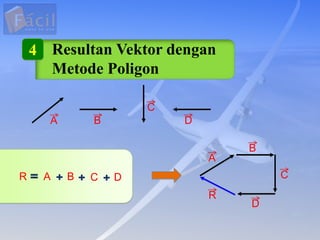
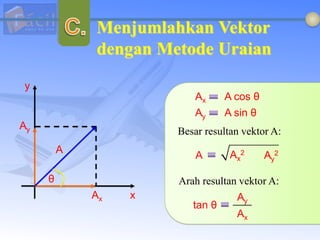
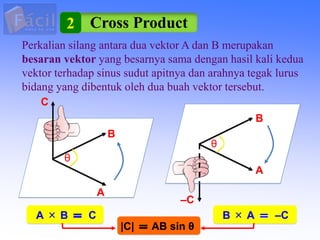
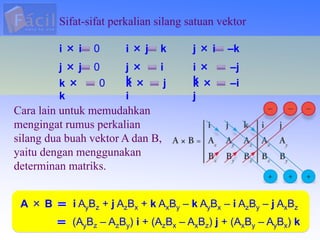
Besaran vektor memiliki nilai dan arah, sedangkan besaran skalar hanya memiliki nilai. Vektor ditandai dengan panah atas huruf atau huruf tebal. Penjumlahan vektor dapat dilakukan secara grafis, analitis, poligon, atau uraian. Perkalian titik menghasilkan skalar sedangkan perkalian silang menghasilkan vektor tegak lurus.

1. Besaran Vektor
Advanced Learning Physic 1A

3. Notasi Vektor
Besaran yang memiliki nilai dan arah disebut besaran vektor,
sedangkan besaran yang hanya memiliki nilai saja disebut
besaran skalar.
Bisakah Anda menyebutkan contoh
besaran vektor dan besaran skalar?
Sebuah vektor digambarkan oleh sebuah anak panah. Panjang anak
panah mewakili besar atau nilai vektor, sedangkan arah anak panah
mewakili arah vektor.
Notasi sebuah vektor dinyatakan oleh huruf yang ditandai dengan
anak panah di atasnya atau hurufnya dicetak tebal.
A A

4. Penjumlahan Vektor
Menggunakan Metode
Grafis dan Analisis
Resultan Dua Vektor Sejajar
1
A B R A B
2 N 3 N 5 N
A B R –A B
2 N 3 N 1 N

5. Resultan Dua Vektor yang Saling
Tegak Lurus
2
A
B
R
R A2 B2
Besar resultan vektor A dan B adalah:

6. Resultan Dua Vektor yang
Mengapit Sudut < 90°
3
A
R
Besar resultan vektor A dan B adalah:
B
θ
R A2 B2
2AB cos θ

7. Resultan Vektor dengan
Metode Poligon
4
A B
C
D
R A B C D
A
B
C
D
R

8. Menjumlahkan Vektor
dengan Metode Uraian
Ay
A Ax
2
Ay
2
Besar resultan vektor A:
y
Ax
A
x
θ
Ax A cos θ
Ay A sin θ
Arah resultan vektor A:
tan θ
Ay
Ax

9. Perkalian Vektor
Dot Product
1
Perkalian titik antara dua vektor A dan B merupakan besaran
skalar yang besarnya sama dengan hasil kali kedua vektor
terhadap cosinus sudut apitnya.
A cos θ
A
B
θ
A  B AB cos θ

10. Sifat-sifat perkalian titik satuan vektor
i  i 1
j  j k  k Sudut yang mengapit
0°
i  j 0
i  k j  k Sudut yang mengapit
90°
Secara matematis, perkalian titik vektor A dan B adalah
A  B (Axi + Ayj + Azk)  (Bxi + Byj + Bzk)
maka A  B AxBx + AyBy + AzBz

11. Cross Product
2
Perkalian silang antara dua vektor A dan B merupakan
besaran vektor yang besarnya sama dengan hasil kali kedua
vektor terhadap sinus sudut apitnya dan arahnya tegak lurus
bidang yang dibentuk oleh dua buah vektor tersebut.
A
B
C
θ
–C
A
B
θ
A × B C B × A –C
AB sin θ
|C|

12. Sifat-sifat perkalian silang satuan vektor
i × i 0 i × j k j × i –k
j × j 0 j ×
k
i i ×
k
–j
k ×
k
0 k ×
i
j k ×
j
–i
Cara lain untuk memudahkan
mengingat rumus perkalian
silang dua buah vektor A dan B,
yaitu dengan menggunakan
determinan matriks.
A × B i AyBz + j AzBx + k AxBy – k AyBx – i AzBy – j AxBz
(AyBz – AzBy) i + (AzBx – AxBz) j + (AxBy – AyBx) k

13. Kesimpulan
Kesimpulan
Besaran skalar adalah besaran yang hanya memiliki nilai
saja dan tidak memiliki arah.
Besaran vektor adalah besaran yang memiliki nilai
dan arah.
Notasi atau simbol sebuah vektor dapat menggunakan satu
atau dua huruf dengan tanda panah di atasnya atau dengan
dicetak tebal.
Penjumlahan vektor dapat menggunakan metode
grafis, analitis, poligon, dan uraian.

14. 1. Dua vektor memiliki titik pangkal berimpit. Nilai tiap
vektor adalah 6 satuan dan 8 satuan. Hitung nilai dan arah
resultan kedua vektor tersebut jika sudut apitnya 90°.
2. Sebuah vektor F memiliki panjang 50 satuan membentuk
sudut 135° terhadap sumbu-x positif. Tentukanlah
komponen-komponen vektor F terhadap sumbu-x dan
sumbu-y.
3. F2 = 12 N
45
°
F3 = 24 N
30
°
60
°
F1 = 24 N
F4 = 12 N
x
y
Hitunglah nilai dan
arah resultannya.
Kuis

15. Terima Kasih
“gagal merencanakan berarti merencanakan
kegagalan.”
– NN –

16. CD images
media.thestar.topscms
wikimedia.org
Referensi

17. Editor
Gungun Gunawan
Layouter
Rabi Januar