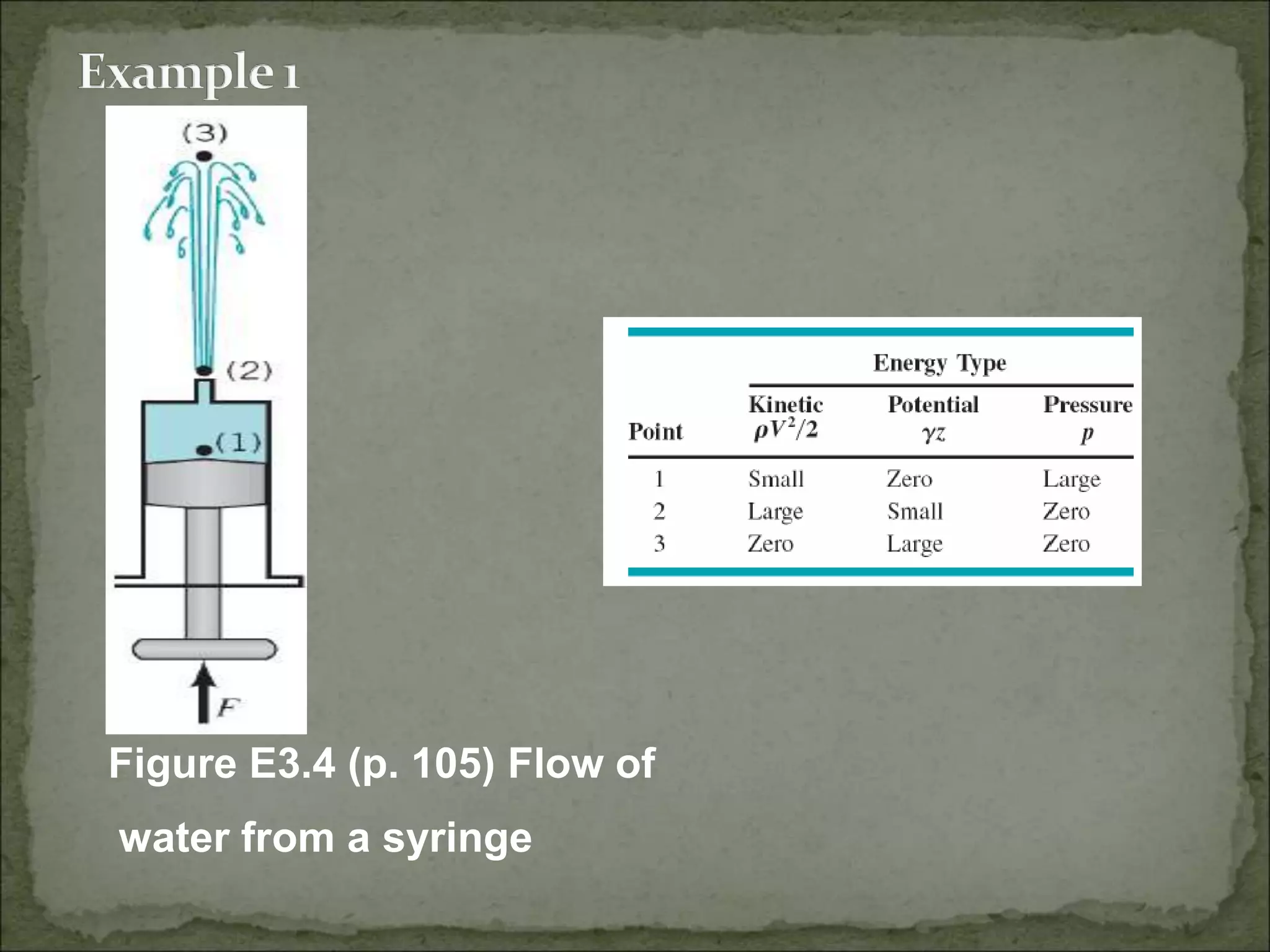
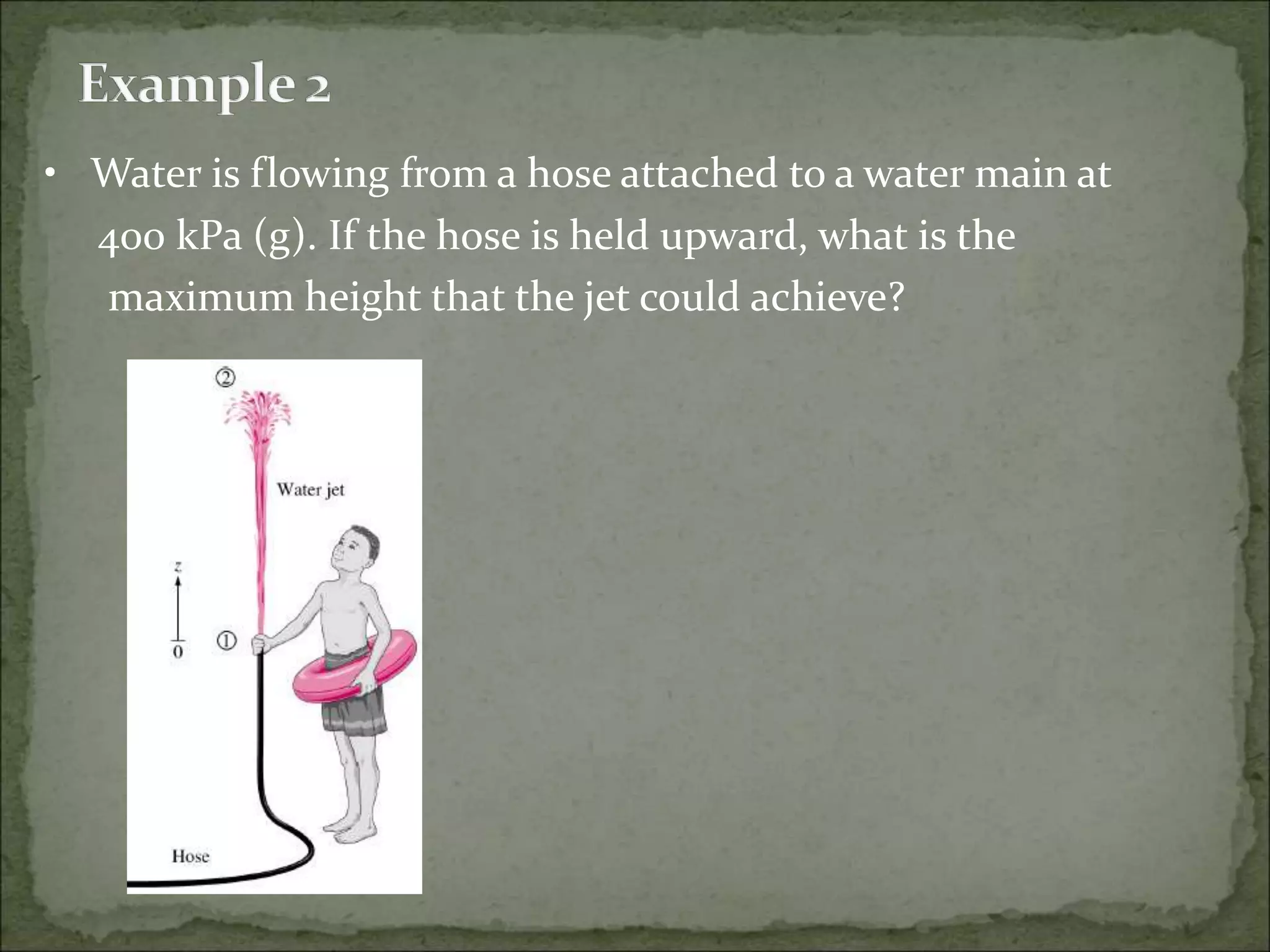
The document discusses principles of fluid flow, specifically focusing on incompressible, steady flow and the relationship between pressure, velocity, and elevation as described by Bernoulli's equation. It outlines conditions under which these principles apply, including the effects of friction and changes in flow conditions. Various equations and scenarios, such as water flow from a nozzle and a tank, are presented to illustrate these concepts.

1. • It is an approximate relation between pressure,
velocity and elevation
• It is valid in regions of steady, incompressible
flow
where net frictional forces are negligible
• Viscous effects are negligible compared to
inertial,
gravitational and pressure effects.
Applicable to in viscid regions of flow (flow
regions outside of boundary layers)
• Steady flow (no change with time at a specified
location)

2. • The value of a quantity may change from one location to
another. In the case of a garden hose nozzle, the velocity of
water remains constant at a specified location but it changes
from the inlet to the exit (water accelerates along the nozzle).

3. • Motion of a particle in terms of
distance “s” along a streamline
• Velocity of the particle, V = ds/dt,
which may vary along the streamline
• In 2-D flow, the acceleration is
decomposed into two components,
streamwise acceleration as, and
normal acceleration, an.
2
n
V
a
R

• For particles that move along a straight path, an =0

4. • Velocity of a particle, V
(s, t) = function of s, t
• Total differential
• In steady flow,
• Acceleration,
V V
dV ds dt
s t
 
 
 
or
dV V ds V
dt s dt t
 
 
 
0;and ( )
V
V V s
t

  

s
dV V ds V dV
a V V
dt s dt s ds
 
   
 

5. • Applying Newton’s second law of conservation of linear
momentum relation in the flow field
( ) sin
dV
PdA P dP dA W mV
ds

   
ds is the mass
m V dA
 
     
W=mg= g ds is the weight of the fluid
dA
    
sin =dz/ds

- -
dz dV
dpdA gdAds dAdsV
ds ds
 

,
dp gdz VdV
 
  
2
1
Note V dV= ( ),and divding by
2
d V 
2
1
( ) 0
2
dp
d V gdz

  
Substituting,
Canceling dA from each term and simplifying,

6.  Integrating
2
constant (along a streamline)
2
dp V
gz

  

2
constant (along a streamline)
2
p V
gz

  
For steady flow
For steady incompressible flow,

7. • Bernoulli Equation states
that the sum of kinetic,
potential and flow (pressure)
energies of a fluid particle is
constant along a streamline
during steady flow.
• Between two points:
2 2
1 1 2 2
1 2 or,
2 2
p V p V
gz gz
 
    
2 2
1 1 2 2
1 2
2 2
p V p V
z z
g g
    
 
2
pressure head; velocity head, z=elevation head
2
p V
g
 


8. Figure E3.4 (p. 105) Flow of
water from a syringe

9. • Water is flowing from a hose attached to a water main at
400 kPa (g). If the hose is held upward, what is the
maximum height that the jet could achieve?

10. • Water discharge from a large tank. Determine the water
velocity at the outlet.

11.  change in flow conditions
• Frictional effects can not be neglected in long and narrow
flow passage, diverging flow sections, flow separations
• No shaft work