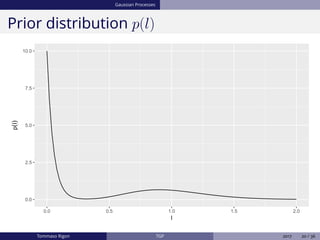
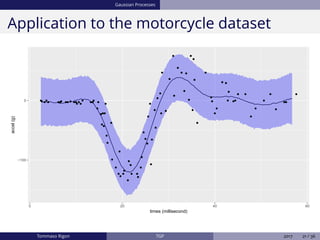
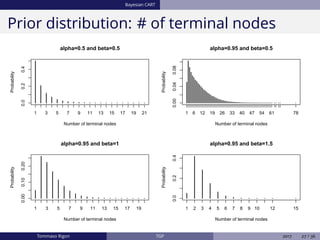
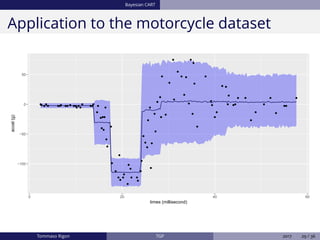
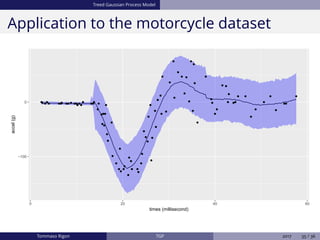
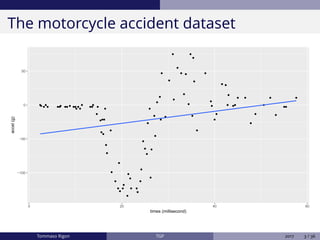
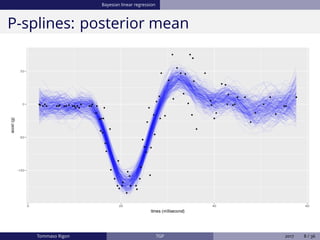
The document discusses Bayesian regression and treed Gaussian process models, highlighting their applications in flexible mean process estimation and uncertainty quantification. It reviews various Bayesian methods for regression, including Bayesian linear regression, Gaussian processes, and Bayesian CART models, detailing their formulations and computational approaches. It also emphasizes advantages and disadvantages of Gaussian processes and presents a case study on the motorcycle accident dataset.








![Gaussian Processes
Gaussian processes
Finite dimensional distributions
By definition, for each finite collection of points x = (x1, . . . , xn) all in X we
have that the vector f(x) = (f(x1), . . . , f(xn)) is distributed according to
f(x) ∼ Nn(m(x), K(x, x)),
where m(x) is the n-dimensional mean vector generated by the mean
function and K(x, x) is a n × n covariance matrix generated by k(·, ·) by
setting [K(x, x)]ij = k(xi, xj), for i, j = 1, . . . , n.
Notation
Let x and x be two collections of points in X and let f(x) and f(x ) be the
associated random variables. We let
Cov (f(x), f(x )) = K(x, x ).
Tommaso Rigon TGP 2017 11 / 36](https://image.slidesharecdn.com/rigon-180123163739/85/Bayesian-regression-models-and-treed-Gaussian-process-models-11-320.jpg)