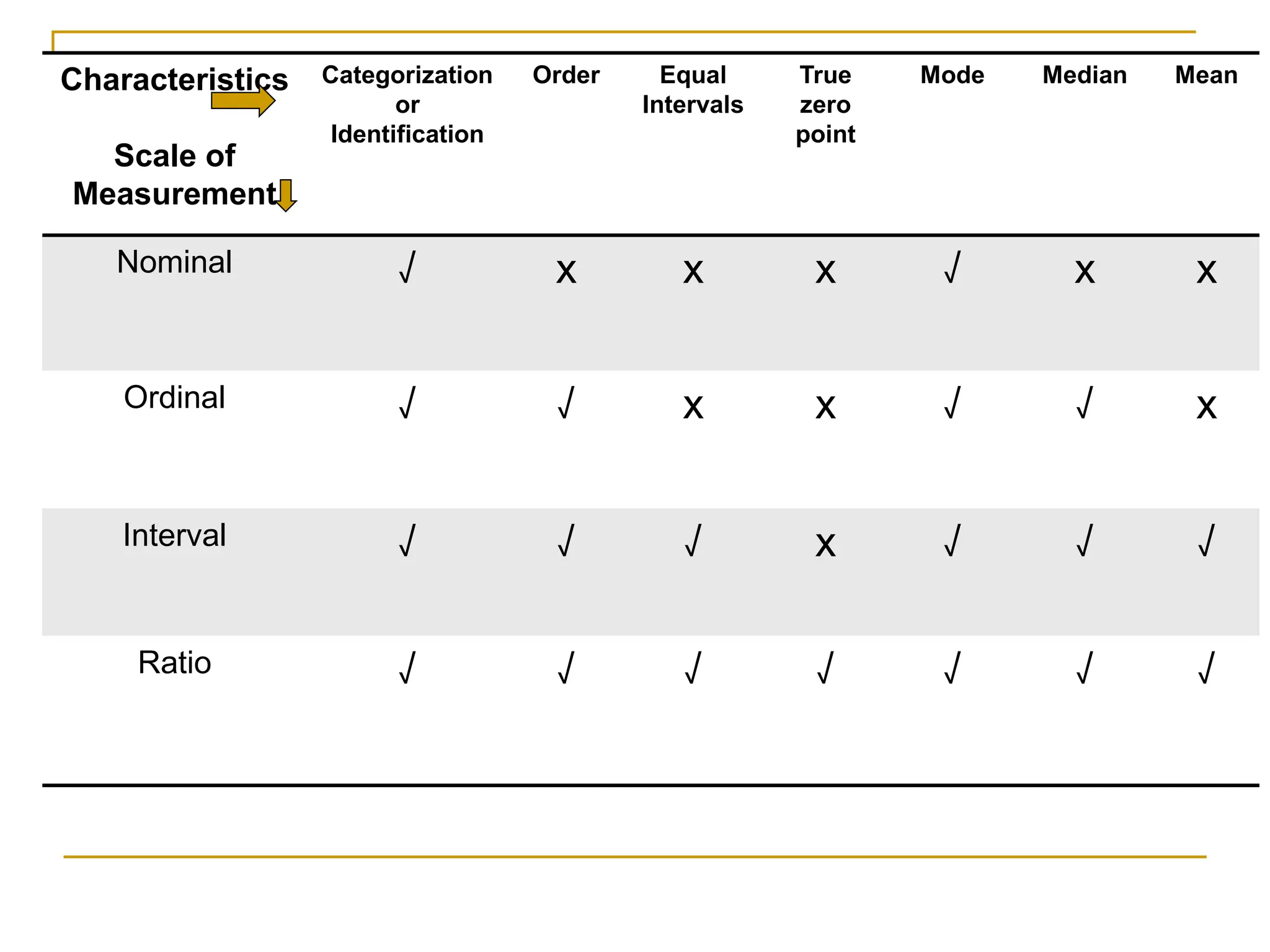
This document provides an introduction and overview of research methods and statistics. It begins by outlining the origins and early contributors to statistics as a field, including its use in state administration starting in the 17th century. Key concepts in statistics such as variables, populations, samples, and levels of measurement are then defined. The document distinguishes between descriptive and inferential statistics, outlining common techniques for each. It concludes by discussing the scope and limitations of statistics as a scientific discipline.

1. Research Methods
and
Statistics

2. Introduction
 The term ‘Statistics’ was used for the first
time by the German writer Gottfried
Achenwall in the year 1749
 Some scholars pinpoint the origin of
statistics to 1662, with the publication of
"Observations on the Bills of Mortality"
by John Graunt.

3.  Francis Galton and Charles Darwin
through the study of genetic theories,
contributed to application of statistical
methodology (the study of regression and
correlation in biological measurements -
18th century)

4.  Karl Pearson (1857-1936 : University
college, London) continued in the tradition
of Galton and laid the foundation for
descriptive and correlational statistics.
 The dominant person in statistics and
biometry has been Ronald A Fisher (1890
– 1962). His contributions to the Analysis
of Variance brought remarkable
improvements in the scope of statistics.

5. Origin of Statistics
The word statistics has been derived from
the following words:
 Latin word Status
 Italian word Statista
 German word Statistik
All these words mean a political state

6.  In the early years, statistics meant a
collection of facts about the state or the
people in the state for political purposes.
 It helped in collecting data about
economic and social conditions of the
people living in different parts of the
country.
 For proper functioning of the state, it is
essential to know the conditions under
which the people live and work, earn
income and spend the wealth.

7.  This science was known as the science of
state because it was used by the state.
 In this way statistics developed as a
king’s subject or as a science of kings.

8.  The word ‘Statistics’ conveys a variety of
meaning to people. To some ‘Statistics’ is
an imposing form of mathematics, whereas
to others it is tables, charts and figures
found in newspapers, journals, books, TV
reports etc.

9. Almost daily we are exposed to a wide variety
of numerical information which often has a
profound impact on our lives. For Eg.
 India targets doubling exports to $850 billion
by 2017
 about 45% of heart attack victims in India
don’t even reach a hospital
 In India prevalence of HI is 4-5% etc.
These statements contain figures and they are
called numerical statements of facts. An
analysis of such statements can help in
framing suitable policies.

10. The term STATISTICS is used to mean either
statistical data or statistical method
 Quantitative - Whenever, numbers are collected
and compiled, regardless of what they represent,
they become statistics (plural sense – No. of
births, deaths, HI, % of females, average height
etc.)
 Body of theories and techniques - Statistics also
refers to a subject. In this sense statistics is a body
of methods of obtaining and analyzing data in
order to base decisions on them (Singular sense).

11. Definition of Statistics
It is very difficult to give such a
definition of Statistics which may cover
all its broad characteristics.

12. Bowley’s definitions:
1. “Statistics is the science of counting.”
2. “Statistics may rightly be called the
science of average.”
“Statistics are numerical statements of
facts in any department of enquiry placed
in relation to each other”

13. “Statistics are a collection of note-worthy
facts concerning state both historical and
descriptive”
- Achenwall
“Statistics is the science of estimates and
probabilities.”
- Boddington

14. The above given definitions are not
complete to cover all the aspects of
statistics. The definitions given by
Croxton & Cowden (singular sense)
and Horace Secrist (plural sense) are
more exhaustive definitions.

15. Definition in plural sense or in the
sense of numerical data
According to Horace Secrist,
“Statistics are aggregates of facts,
affected to marked extent by multiplicity
of causes, numerically expressed,
enumerated or estimated according to
reasonable standards of accuracy,
collected in a systematic manner for a
pre-determined purpose and placed in
relation to each other.”

16. Characteristics of Statistics:
1. Data should be aggregate of facts and not a single
fact.
2. Fact should be numerically expressed.
3. Facts or data are affected by many factors.
4. Data are enumerated or estimated.
5. The accuracy regarding the data should be observed
to that extent which is reasonably possible.
6. All statistics are numerical statements of facts, but
all numerical statements are not statistics.

17. Definition in singular sense or in the
sense of statistical methodology
Some of the statisticians have defined statistics
in singular sense or as a statistical
methodology. The method by which statistical
data are analysed is called statistical method.
According to Croxton and Cowden Statistics is
defined as “the collection, classification,
analysis and presentation of numerical data”.

18. Thus important features of statistical
methods are as follows:
1. Collection of Data: Under this stage, the
relevant data are collected from various
sources – primary or secondary. Collection
of data is the main and the first step in a
statistical investigation. It depends upon
the objectives of the study. The data are the
bases of the analysis, and should fulfill the
basic objectives of the proposed study.

19. 2. Organisation and presentation of data:
After collection, the data are organised
in a proper form which involves
editing, classification and tabulation.
 Editing is necessary to remove
inconsistencies/ unwanted data.
 Classification means arrangement of
data according to some common
characteristics.
 Tabulation includes presentation of data
in columns and rows.

20. 3. Presentation of data : After
classification, the data are presented in
some suitable manner- either by
diagrams or graphs.

21. 4. Analysis of data: It includes measures of
central tendency, measures of dispersion,
correlation and regression, tests of
comparison etc.. Analysis provides basis
for interpretation.
5. Interpretation: Interpretation of data is
the process of drawing inferences and
conclusions from the analysed data. It
involves statistical thinking, skill,
experience and common sense.

22. Functions of
Statistics

23. The important functions of statistics are
.
1. To present facts in precise / definite form
and simplification of large and complex
data into understandable form.
The data is often large and complex. The
purpose of Statistical methods is to
simplify these complex data and to make
them more understandable.

24. 2. To facilitate comparison:
The main function of statistics is
comparison. It is only by comparison the
significance of certain figures
like averages, percentages, or coefficients,
are inferred.

25. 3. To enlarge individual experience and
knowledge:
Knowledge becomes precise and easy to
understand with the help of statistical
techniques. Because, statistics helps to
present the data in readily comprehensive
form.

26. 4. To study relationship between different
facts:
Another important function of statistics is
investigating the relationship between
two or more phenomenon. The
relationship existing between Height and
weight, Age and hearing loss, Age and
Language score can be measured with the
help of statistical methods like
correlation, regression etc.

27. 5. Helpful in formulation and testing of
hypothesis :
Statistical methods are also employed in
formulating and testing hypothesis.
6. Helpful in forecasting and policy making:
Statistical methods are not only helpful in
estimating the present but they are also
helpful in forecasting the future. Hence
they are helpful in the formulation of
policies.

28. Scope of Statistics / Uses or
Importance of Statistics / Relationship
of Statistics with other sciences
 Statistics and the State
(administration):
 For administrative activity
 To solve various problems and to frame
suitable policies to solve these problems
 Eg. Population control, transport etc.

29.  Statistics and Business:
 Sales prediction with respect to seasonal
and market variations
 Testing the quality of raw materials and
the finished goods by methods of
sampling
 Additional requirements for the product (
to make the product more popular)
 Suitable policies about production,
investment, marketing and sales
management

30.  Statistics and Mathematics:
 Both have helped jointly in the
development of other social and physical
sciences

31.  Statistics and Economics:
 Every branch of Economics takes support
from statistics in order to prove various
Economic theories.
 Econometrics: It is a recent subject. It
studies the application of statistical
techniques to the economical methods. It is
also called as Research Methodology in
Economics.
 Study of Consumption function, production
function, exchange and distribution

32.  Statistics and Physical and Biological
Sciences:
 Physical Sciences like Astronomy, Geology,
Physics etc
 Biological Sciences like Medicines,
Zoology, Botany, Speech and Hearing,
Psychology
 Examples…………..

33.  Biostatistics is defined as the
application of the statistical methods
to the problems of biology,
including human biology, medicine
and public health.

34. Limitations of Statistics:
 Qualitative aspect ignored – The statistical
methods cannot study the nature of
phenomena which cannot be expressed in
quantitative form (statistical techniques may
be applied by reducing the qualitative
expressions to accurate quantitative terms)
 Results are true only on an average – the
laws of statistics are not universal like the
laws of physics, chemistry or astronomy. The
statistical laws are true only on an average.
Statistics is less exact science as compared to
other natural sciences.

35.  Statistics does not deal with individuals
– Statistics deals only with the aggregates
rather than individual items.
 Statistics can be misused – statistics can
be misused by ignorant or wrongly
motivated persons. The data used by
untrained people can lead to misleading
results.
 Only a means and not an end – the tools
of statistics are supposed to be only a
means to understand any given problem
rather than a method to solve any problem

36. DEFINITIONS
 *Variable
 Characteristic or attribute that can assume
different values
*Random Variable
 A variable whose values are determined
by chance.

37. Discrete Variables
 Variables which assume a finite or
countable number of possible values.
Usually obtained by counting.
Continuous Variables
 Variables which assume an infinite
number of possible values. Usually
obtained by measurement.

38. Population
 All subjects possessing a common
characteristic that is being studied.
Sample
 A subgroup or subset of the population.

39. Parameter
 Characteristic or measure obtained from a
population.
Statistic (not to be confused with Statistics)
 Characteristic or measure obtained from a sample.
Qualitative Variables
 Variables which assume non-numerical values.
Quantitative Variables
 Variables which assume numerical values.

40. Descriptive and Inferential Statistics
 Descriptive statistics serve as devices for
organizing data and bringing into focus their
essential characteristics for the purpose of
reaching conclusions at a later stage
 The field of descriptive statistics is not
concerned with the implications or
conclusions that can be drawn from sets of
data. The failure to choose appropriate
descriptive statistics has often been
responsible for faulty scientific inferences.

41. This includes - Collection, organization,
summarization, and presentation of data.
Let us imagine that a behavioral scientist
administrated a number of measuring
instrument (e.g., intelligence tests, personality
inventories, aptitude tests) to a group of high
school students.
1. He may rearrange the scores and group them
in various ways in order to be able to see at a
glance an overall picture of his data
(“Frequency distribution”).

42. 2. He may construct tables, graphs, and
figures to permit visualization of the
results (“Graphing Techniques”).
3. He may convert raw scores to other types
of scores which are more useful for
specific purpose. Thus, he convert these
scores into either percentile ranks, standard
scores, or grades.

43. 4. He may calculate averages, to learn
something about the typical
performances of his subjects.
(“Measures of Central Tendency”)
5. Employing the average as a reference
point, he may describe the dispersion of
scores about this central point. Statistics
which quantify this dispersion are
known as measures of variability or
measures of dispersion.

44. 6. A relationship between two different
measuring instruments may be obtained
using correlation coefficient. For example,
he may wish to determine the relationship
between intelligence and classroom grades.
Once these relationships are established, the
behavioral scientist may employ scores
obtained from one measuring instrument to
predict performance on another
(Regression).

45. INFERENTIAL STATISTICS
This branch of statistics provides the
procedures to draw an inference about
conditions that exist in a larger set of
observations from study of a part of that set.
This helps us in reaching conclusions.
 Generalizing from samples to populations
using probabilities.
 Performing hypothesis testing,
 determining relationships between variables
and making predictions.

46. Examples:
 Does a new therapy technique beneficial for
voice disordered clients?
 Can the effect of noise exposure on hearing
loss be reduced by using ear productive
devices?
 Does hearing aid A increases the gain?
 Is there any significant difference between
normals and experimentals?
 Is there any association between consanguinity
and communication problems?

47. Efficacy of a therapy program may be
tested by randomly selecting two groups :
controls who do not receive the therapy
and experimentals who receive the
therapy. Subject groups can be selected in
such a way that their pre scores must not
have any statistical significance. Final
decision can be made by comparing their
performances of post scores.

48. LEVELS OF MEASURMENTS
There are four levels of measurement:
Nominal, Ordinal, Interval, and Ratio.
These go from lowest level to highest
level. Data is classified according to the
highest level which it fits. Each additional
level adds something the previous level
didn't have.

49.  Nominal is the lowest level. Only names
are meaningful here.
 Ordinal adds an order to the names.
 Interval adds meaningful differences
 Ratio adds a zero so that ratios are
meaningful.

50. NOMINAL SCALES
Observations of unordered variables
constitute a very low measurement and
are referred to as a nominal scale of
measurement. We may assign numerical
values to represent the various classes in a
nominal scale but these numbers have no
quantifying properties. They serve to
identify the classes.

51. EXAMPLES:
1. Numbers on the foot ball players jerseys
2. Normal or experimental
3. Marital status of a person as single,
married, widowed, or divorced. Other
typical examples of nominal variables
are gender, state, vehicle no. plates etc.

52. Nominal data do not share any of the
properties of the numbers we deal in any
other ordinary arithmetic. There is no
order among different outcomes, we can
say only they are “equal” or “not equal”.
For instance, if we record marital status as
1,2,3 or 4 depending on whether the
person is single, married, widowed, or
divorced we cannot write 3>1 or 2<3, and
we cannot write 1+3=4 etc

53. ORDINAL SCALES
The classes in ordinal scales are not
only different from one another (the
characteristic defining nominal scales) but
they stand on some kind of relation to one
another. More specifically, the relationship
are expressed in terms of the algebra of
inequalities: a is less than b (a<b) or a is
greater than b (a>b). Thus the relationships
encountered are: greater, faster, more
severe, more intelligent, more mature,
more disturbed, etc.

54. The numerals employed with ordinal scales
are non-quantitative. They indicate only
position in ordered series and not “how
much” of a difference exists between
successive positions on the scale.
Examples:
1. NAAC rating of colleges as A+, A, B++,
B+, B, C+, C.
2. Very good, good, bad, very bad
3. Strongly agree, agree, disagree
4. Voice roughness is Normal, Slight.
Moderate, Extreme.

55. INTERVAL AND RATIO SCALES
The highest level of measurement
in science is achieved with scales
employing cardinal (fundamental)
numbers (interval or ratio scales). The
numerical values associated with these
scales are truly quantitative and therefore
permit the use of arithmetic operations
such as addition, subtraction,
multiplication and division

56. There are two types of scales based
upon cardinal numbers: interval and ratio
scale. The only difference between the
two scales is that the interval scale
employs an arbitrary zero point, where as
ratio scale employs natural or true zero
point. A good example of the difference
between an interval and a ratio scale is
height as measured from a table top
(interval) vs. height measured from the
floor (ratio).

57. What is a natural (true) zero?
Some scales of measurement have a
natural zero and some do not. For
example, height, weight etc have a natural
0 at no height or no weight.
Consequently, it makes sense to say that
2m is twice as large as 1m. Both of these
variables are ratio scale.

58. On the other hand, year, time and
temperature (C) do not have a natural zero.
The year 0 is arbitrary Similarly, 00 C is
arbitrary (freezing point of water) and 0:00
hr refers to 120 clock. All these variables
are interval scale.

59. Characteristics
Scale of
Measurement
Categorization
or
Identification
Order Equal
Intervals
True
zero
point
Mode Median Mean
Nominal √ x x x √ x x
Ordinal √ √ x x √ √ x
Interval √ √ √ x √ √ √
Ratio √ √ √ √ √ √ √