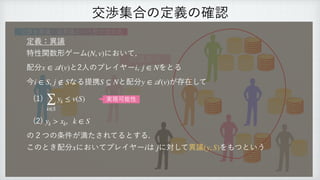
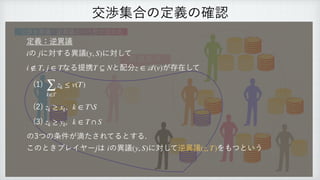
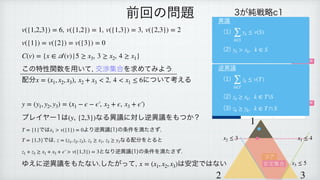
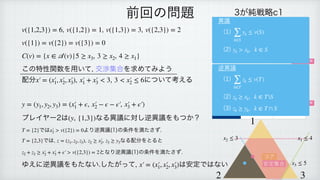
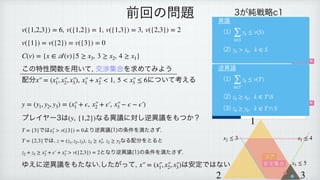
This document discusses game theory and bargaining sets. It begins by reviewing the definitions of objections and counter-objections in bargaining situations. It then proves that the bargaining set of a game is always non-empty using the relationship between the bargaining set and the core. As an example, it calculates the core and examines different allocations to determine which belong to the bargaining set for a specific characteristic function game.

1. ゲーム理論 BASIC 演習4
交渉集合を求める

2. 1. 交渉集合の定義の確認
2. コアと交渉集合
3. 前回の問題

3. 交渉集合の定義の確認
異議あり
交渉を異議・逆異議という形で定式化
定義：異議
特性関数形ゲーム において,
配分 と2人のプレイヤー をとる
今 , なる提携 と配分 が存在して
(1)
(2)
の２つの条件が満たされてるとする.
このとき配分 においてプレイヤー は に対して異議 をもつという
(N, v)
x ∈
𝒜
(v) i, j ∈ N
i ∈ S j ∉ S S ⊆ N y ∈
𝒜
(v)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
x i j (y, S)
実現可能性

4. 交渉集合の定義の確認
異議あり
交渉を異議・逆異議という形で定式化
定義：逆異議
の に対する異議 に対して
, なる提携 と配分 が存在して
(1)
(2)
(3)
の3つの条件が満たされてるとする.
このときプレイヤー は の異議 に対して逆異議 をもつという
i j (y, S)
i ∉ T j ∈ T T ⊆ N z ∈
𝒜
(v)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S
j i (y, S) (z, T)

5. 交渉集合の定義の確認
定義：交渉集合
配分 において, どのプレイヤーも異議をもたないか
ないしは異議をもつプレイヤーがいたとしても,
それに対する逆異議が存在するとき, 配分 は安定であるといい,
安定な配分の全体を交渉集合という
ゲーム における交渉集合を で表す
x ∈
𝒜
(v)
x
(N, v) ℬ(v)

6. コアと交渉集合
定理：コアと交渉集合の関係
ゲーム において, コアを , 交渉集合を とすると
＊交渉集合は常に非空である(別機会に証明)
(証明)コア であれば明らか. とする. ではないと仮定し, をとる.
であるため, あるプレイヤー から に対する異議が存在する. すなわち
ある提携 , , と , となる が存在する. このとき
となり, に矛盾する.
(N, v) C(v) ℬ(v) C(v) ⊆ ℬ(v)
C(v) = ∅ C(v) ≠ ∅ C(v) ⊆ ℬ(v) x ∈ C(v)ℬ(v)
x ∉ ℬ(v) i j
S i ∈ S j ∉ S
∑
k∈S
yk ≤ v(S) yk > xk, k ∈ S y
∑
k∈S
xk <
∑
k∈S
yk ≤ v(S)
x ∈ C(v)

7. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合

8. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
このゲームはコアが存在するため,
定理から交渉集合に含まれる.
コアに含まれない配分について異議/逆異議を調べる
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合

9. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
配分 , について考える
まず, かつ , であるため,
プレイヤー は他のプレイヤーに対して異議をもたない.
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x = (x1, x2, x3), x2 + x3 < 2 4 < x1 ≤ 6
4 < x1 v({1,2}) = 1 v({1,3}) = 3
1
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合
異議
(1)
(2)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
逆異議
(1)
(2)
(3)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S

10. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
配分 , について考える
プレイヤー2はプレイヤー1に対して必ず異議をもつ
ただし , である
この配分は以下を満たす
(1)
(2)
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x = (x1, x2, x3), x2 + x3 < 2 4 < x1 ≤ 6
y = (y1, y2, y3) = (x1 − ϵ − ϵ′

, x2 + ϵ, x3 + ϵ′

)
x2 + ϵ + x3 + ϵ′

= 2 ϵ > 0, ϵ′

> 0
y2 + y3 ≤ v({2,3}) = 2
y2 > x2, y3 > x3
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合
異議
(1)
(2)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
逆異議
(1)
(2)
(3)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S

11. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
配分 , について考える
プレイヤー1は なる異議に対し逆異議をもつか？
では より逆異議(1)の条件を満たさず.
では, , なる配分をとると
となり逆異議(1)の条件を満たさず.
ゆえに逆異議をもたない.したがって, は安定ではない
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x = (x1, x2, x3), x2 + x3 < 2 4 < x1 ≤ 6
y = (y1, y2, y3) = (x1 − ϵ − ϵ′

, x2 + ϵ, x3 + ϵ′

)
(y, {2,3})
T = {1} x1 > v({1}) = 0
T = {1,3} z = (z1, z2, z3) z1 ≥ x1, z3 ≥ y3
z1 + z3 ≥ x1 + x3 + ϵ′

> v({1,3}) = 3
x = (x1, x2, x3)
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合
異議
(1)
(2)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
逆異議
(1)
(2)
(3)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S

12. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
配分 , について考える
まず, かつ , であるため,
プレイヤー は他のプレイヤーに対して異議をもたない.
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x′

= (x′

1, x′

2, x′

3), x′

1 + x′

3 < 3 3 < x′

2 ≤ 6
3 < x′

2 v({1,2}) = 1 v({2,3}) = 2
2
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合
異議
(1)
(2)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
逆異議
(1)
(2)
(3)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S

13. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
配分 , について考える
プレイヤー1はプレイヤー2に対して必ず異議をもつ
ただし , である
この配分は以下を満たす
(1)
(2)
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x′

= (x′

1, x′

2, x′

3), x′

1 + x′

3 < 3 3 < x′

2 ≤ 6
y = (y1, y2, y3) = (x′

1 + ϵ, x′

2 − ϵ − ϵ′

, x′

3 + ϵ′

)
x′

1 + ϵ + x′

3 + ϵ′

= 3 ϵ > 0, ϵ′

> 0
y1 + y3 ≤ v({1,3}) = 3
y1 > x′

1, y3 > x′

3
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合
異議
(1)
(2)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
逆異議
(1)
(2)
(3)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S

14. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
配分 , について考える
プレイヤー2は なる異議に対し逆異議をもつか？
では より逆異議(1)の条件を満たさず.
では, , なる配分をとると
となり逆異議(1)の条件を満たさず.
ゆえに逆異議をもたない.したがって, は安定ではない
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x′

= (x′

1, x′

2, x′

3), x′

1 + x′

3 < 3 3 < x′

2 ≤ 6
y = (y1, y2, y3) = (x′

1 + ϵ, x′

2 − ϵ − ϵ′

, x′

3 + ϵ′

)
(y, {1,3})
T = {2} x′

2 > v({2}) = 0
T = {2,3} z = (z1, z2, z3) z2 ≥ x′

2, z3 ≥ y3
z2 + z3 ≥ x′

2 + x′

3 + ϵ′

> v({2,3}) = 2
x′

= (x′

1, x′

2, x′

3)
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合
異議
(1)
(2)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
逆異議
(1)
(2)
(3)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S

15. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
配分 , について考える
まず, かつ , であるため,
プレイヤー は他のプレイヤーに対して異議をもたない.
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x′

′

= (x′

′

1, x′

′

2, x′

′

3), x′

′

1 + x′

′

2 < 1 5 < x′

′

3 ≤ 6
5 < x′

′

3 v({1,3}) = 3 v({2,3}) = 2
3
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合
異議
(1)
(2)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
逆異議
(1)
(2)
(3)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S

16. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
配分 , について考える
プレイヤー1はプレイヤー3に対して必ず異議をもつ
ただし , である
この配分は以下を満たす
(1)
(2)
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x′

′

= (x′

′

1, x′

′

2, x′

′

3), x′

′

1 + x′

′

2 < 1 5 < x′

′

3 ≤ 6
y = (y1, y2, y3) = (x′

′

1 + ϵ, x′

′

2 + ϵ′

, x′

′

3 − ϵ − ϵ′

)
x′

′

1 + ϵ + x′

′

2 + ϵ′

= 1 ϵ > 0, ϵ′

> 0
y1 + y1 ≤ v({1,2}) = 1
y1 > x′

′

1, y2 > x′

′

2
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合
異議
(1)
(2)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
逆異議
(1)
(2)
(3)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S

17. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
配分 , について考える
プレイヤー3は なる異議に対し逆異議をもつか？
では より逆異議(1)の条件を満たさず.
では, , なる配分をとると
となり逆異議(1)の条件を満たさず.
ゆえに逆異議をもたない.したがって, は安定ではない
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x′

′

= (x′

′

1, x′

′

2, x′

′

3), x′

′

1 + x′

′

2 < 1 5 < x′

′

3 ≤ 6
y = (y1, y2, y3) = (x′

′

1 + ϵ, x′

′

2 + ϵ′

, x′

′

3 − ϵ − ϵ′

)
(y, {1,2})
T = {3} x′

′

3 > v({3}) = 0
T = {2,3} z = (z1, z2, z3) z3 ≥ x′

′

3, z2 ≥ y2
z2 + z3 ≥ x′

′

2 + ϵ′

+ x′

′

3 > v({2,3}) = 2
x′

′

= (x′

′

1, x′

′

2, x′

′

3)
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合
異議
(1)
(2)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
逆異議
(1)
(2)
(3)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S

18. , , ,
この特性関数を用いて, 交渉集合を求めてみよう
以上より, 交渉集合はコアに一致する.
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
前回の問題 3が純戦略c1
1＼2 b1 b2
a1 1, 1, 1 2, 0, 0
a2 0, 0, 2 2, 2, 1
3が純戦略c2
1＼2 b1 b2
a1 1, 0, 2 0, 0, 3
a2 3, 2, 1 0, 1, 0
ナッシュ均衡
ナッシュ均衡
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
コア
安定集合
異議
(1)
(2)
∑
k∈S
yk ≤ v(S)
yk > xk, k ∈ S
逆異議
(1)
(2)
(3)
∑
k∈T
zk ≤ v(T)
zk ≥ xk, k ∈ TS
zk ≥ yk, k ∈ T ∩ S
交渉集合

19. ゲーム理論 BASIC 演習4
交渉集合を求める
次回： 演習5