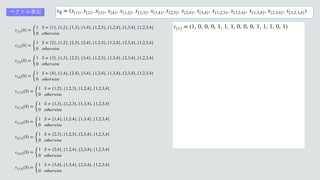
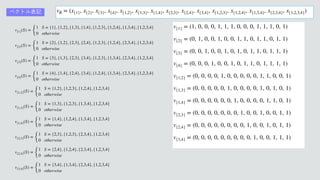
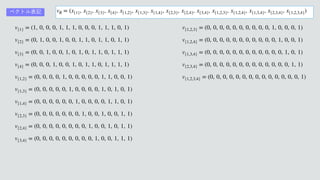
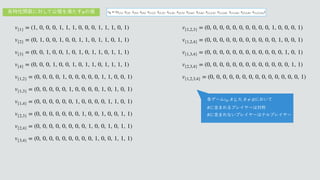
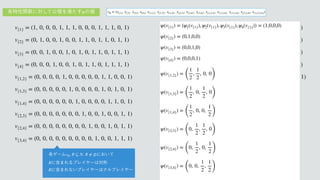
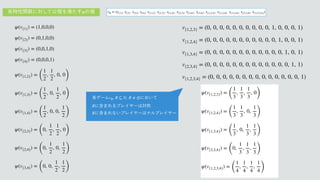
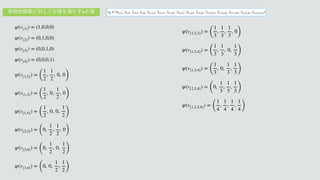
1. The document defines a set of valuation functions vS over subsets S of a set N. Each vS assigns a value of 1 if S is the argument and 0 otherwise. 2. It specifies the valuation functions for all singletons, pairs, triples and the full set of N. 3. It defines a vector φ of these valuation functions to represent a valuation v over N.

1. ήʔϜཧ࿦#4*$ԋश
ਓήʔϜͷγϟʔϓϨΠ஋Λ‫ٻ‬ΊΔ

2. γϟʔϓϨΠ஋ͷఆٛ
ͭͷެཧ
ਓήʔϜʹ͓͚Δ‫ج‬ఈͱͳΔಛੑؔ਺
γϟʔϓϨΠ஋Λ‫ٻ‬ΊΔ

3. γϟʔϓϨΠ஋ͷఆٛ
ఆٛɿγϟʔϓϨΠ஋
ಛੑؔ਺‫ܗ‬ήʔϜ ʹ͓͍ͯ
ਓͣͭϓϨΠϠʔ͕ՃΘΓશମఏ‫ܗ͕ܞ‬੒͞ΕΔ ‫ݸ‬ͷఏ‫ܗܞ‬੒͕
͢΂ͯಉ֬͡཰Ͱ‫͜ى‬Δͱ͢Δ͜ͷͱ͖ͷ֤ϓϨΠϠʔͷߩ‫౓ݙ‬ͷ‫ظ‬଴஋Λ ʹ͓͚Δ
֤ϓϨΠϠʔͷγϟʔϓϨΠ஋ͱ͍͏ϓϨΠϠʔ ͷγϟʔϓϨΠ஋Λ ͱ͢Δͱ
Λ୯ʹγϟʔϓϨΠ஋ͱ͍͏
ผද‫ݱ‬
(N, v) n!
(N, v)
i ϕi(v)
ϕi(v) =
1
n! ∑
π∈Π
(v(Pπ,i
∪ {i}) − v(Pπ,i
))
ϕ(v) = (ϕ1(v)⋯, ϕn(v))
ϕi(v) =
1
n! ∑
S:S⊆N,i∉S
s!(n − s − 1)!(v(S ∪ {i}) − v(S)), ∀i ∈ N

4. ͭͷެཧ
ެཧશମ߹ཧੑ
೚ҙͷ ʹରͯ͠
ެཧφϧϓϨΠϠʔʹؔ͢Δੑ࣭
೚ҙͷ ʹରͯ͠
ϓϨΠϠʔ ͕φϧϓϨΠϠʔͰ͋Ε͹
ެཧରশੑ
೚ҙͷ ʹରͯ͠
ϓϨΠϠʔ ͕ ʹ͓͍ͯରশͰ͋Ε͹
ެཧՃ๏ੑ
೚ҙͷ ʹରͯ͠
v ∈ V
∑
i∈N
ψi(v) = v(N)
v ∈ V i ∈ N ψi(v) = 0
v ∈ V i, j (N, v) ψi(v) = ψj(v)
v, u ∈ V ψi(v + u) = ψi(v) + ψi(u) ∀i ∈ N

5. ਓήʔϜͷ‫ج‬ఈͱͳΔಛੑؔ਺
v{1}(S) =
{
1 S = {1}, {1,2}, {1,3}, {1,4}, {1,2,3}, {1,2,4}, {1,3,4}, {1,2,3,4}
0 otherwise
v{2}(S) =
{
1 S = {2}, {1,2}, {2,3}, {2,4}, {1,2,3}, {1,2,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{3}(S) =
{
1 S = {3}, {1,3}, {2,3}, {3,4}, {1,2,3}, {1,3,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{4}(S) =
{
1 S = {4}, {1,4}, {2,4}, {3,4}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{1,2}(S) =
{
1 S = {1,2}, {1,2,3}, {1,2,4}, {1,2,3,4}
0 otherwise
v{1,3}(S) =
{
1 S = {1,3}, {1,2,3}, {1,3,4}, {1,2,3,4}
0 otherwise
v{1,4}(S) =
{
1 S = {1,4}, {1,2,4}, {1,3,4}, {1,2,3,4}
0 otherwise
v{2,3}(S) =
{
1 S = {2,3}, {1,2,3}, {2,3,4}, {1,2,3,4}
0 otherwise
v{2,4}(S) =
{
1 S = {2,4}, {1,2,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{3,4}(S) =
{
1 S = {3,4}, {1,3,4}, {2,3,4}, {1,2,3,4}
0 otherwise
‫ج‬ఈͱͳΔಛੑؔ਺
ิ଍
‫ݸ‬ͷҎԼͷ‫ج‬ఈͱͳΔಛੑؔ਺͕ଘࡏ͢Δɿ
೚ҙͷఏ‫ܞ‬ ʹରͯ͠
v{1,2,3}(S) =
{
1 S = {1,2,3}, {1,2,3,4}
0 otherwise
v{1,2,4}(S) =
{
1 S = {1,2,4}, {1,2,3,4}
0 otherwise
v{1,3,4}(S) =
{
1 S = {1,3,4}, {1,2,3,4}
0 otherwise
v{2,3,4}(S) =
{
1 S = {2,3,4}, {1,2,3,4}
0 otherwise
v{1,2,3,4}(S) =
{
1 S = {1,2,3,4}
0 otherwise
24
− 1 = 15
R ⊆ N, R ≠ ∅
vR(S) =
{
1 R ⊆ S
0 otherwise

6. ਓήʔϜͷ‫ج‬ఈͱͳΔಛੑؔ਺
v{1}(S) =
{
1 S = {1}, {1,2}, {1,3}, {1,4}, {1,2,3}, {1,2,4}, {1,3,4}, {1,2,3,4}
0 otherwise
v{2}(S) =
{
1 S = {2}, {1,2}, {2,3}, {2,4}, {1,2,3}, {1,2,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{3}(S) =
{
1 S = {3}, {1,3}, {2,3}, {3,4}, {1,2,3}, {1,3,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{4}(S) =
{
1 S = {4}, {1,4}, {2,4}, {3,4}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{1,2}(S) =
{
1 S = {1,2}, {1,2,3}, {1,2,4}, {1,2,3,4}
0 otherwise
v{1,3}(S) =
{
1 S = {1,3}, {1,2,3}, {1,3,4}, {1,2,3,4}
0 otherwise
v{1,4}(S) =
{
1 S = {1,4}, {1,2,4}, {1,3,4}, {1,2,3,4}
0 otherwise
v{2,3}(S) =
{
1 S = {2,3}, {1,2,3}, {2,3,4}, {1,2,3,4}
0 otherwise
v{2,4}(S) =
{
1 S = {2,4}, {1,2,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{3,4}(S) =
{
1 S = {3,4}, {1,3,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{1,2,3}(S) =
{
1 S = {1,2,3}, {1,2,3,4}
0 otherwise
v{1,2,4}(S) =
{
1 S = {1,2,4}, {1,2,3,4}
0 otherwise
v{1,3,4}(S) =
{
1 S = {1,3,4}, {1,2,3,4}
0 otherwise
v{2,3,4}(S) =
{
1 S = {2,3,4}, {1,2,3,4}
0 otherwise
v{1,2,3,4}(S) =
{
1 S = {1,2,3,4}
0 otherwise
ϕΫτϧද‫ه‬ vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})
v{1} = (1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1)

7. ਓήʔϜͷ‫ج‬ఈͱͳΔಛੑؔ਺
v{1}(S) =
{
1 S = {1}, {1,2}, {1,3}, {1,4}, {1,2,3}, {1,2,4}, {1,3,4}, {1,2,3,4}
0 otherwise
v{2}(S) =
{
1 S = {2}, {1,2}, {2,3}, {2,4}, {1,2,3}, {1,2,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{3}(S) =
{
1 S = {3}, {1,3}, {2,3}, {3,4}, {1,2,3}, {1,3,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{4}(S) =
{
1 S = {4}, {1,4}, {2,4}, {3,4}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{1,2}(S) =
{
1 S = {1,2}, {1,2,3}, {1,2,4}, {1,2,3,4}
0 otherwise
v{1,3}(S) =
{
1 S = {1,3}, {1,2,3}, {1,3,4}, {1,2,3,4}
0 otherwise
v{1,4}(S) =
{
1 S = {1,4}, {1,2,4}, {1,3,4}, {1,2,3,4}
0 otherwise
v{2,3}(S) =
{
1 S = {2,3}, {1,2,3}, {2,3,4}, {1,2,3,4}
0 otherwise
v{2,4}(S) =
{
1 S = {2,4}, {1,2,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{3,4}(S) =
{
1 S = {3,4}, {1,3,4}, {2,3,4}, {1,2,3,4}
0 otherwise
v{1,2,3}(S) =
{
1 S = {1,2,3}, {1,2,3,4}
0 otherwise
v{1,2,4}(S) =
{
1 S = {1,2,4}, {1,2,3,4}
0 otherwise
v{1,3,4}(S) =
{
1 S = {1,3,4}, {1,2,3,4}
0 otherwise
v{2,3,4}(S) =
{
1 S = {2,3,4}, {1,2,3,4}
0 otherwise
v{1,2,3,4}(S) =
{
1 S = {1,2,3,4}
0 otherwise
ϕΫτϧද‫ه‬ vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})
v{1} = (1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1)
v{2} = (0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1)
v{3} = (0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1)
v{4} = (0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1)
v{1,2} = (0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1)
v{1,3} = (0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1)
v{1,4} = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1)
v{2,3} = (0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1)
v{2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1)
v{3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1)

8. ਓήʔϜͷ‫ج‬ఈͱͳΔಛੑؔ਺
v{1} = (1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1)
v{2} = (0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1)
v{3} = (0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1)
v{4} = (0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1)
v{1,2} = (0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1)
v{1,3} = (0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1)
v{1,4} = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1)
v{2,3} = (0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1)
v{2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1)
v{3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1)
v{1,2,3}(S) =
{
1 S = {1,2,3}, {1,2,3,4}
0 otherwise
v{1,2,4}(S) =
{
1 S = {1,2,4}, {1,2,3,4}
0 otherwise
v{1,3,4}(S) =
{
1 S = {1,3,4}, {1,2,3,4}
0 otherwise
v{2,3,4}(S) =
{
1 S = {2,3,4}, {1,2,3,4}
0 otherwise
v{1,2,3,4}(S) =
{
1 S = {1,2,3,4}
0 otherwise
ϕΫτϧද‫ه‬ vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})
v{1,2,3} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1)
v{1,2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1)
v{1,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1)
v{2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1)
v{1,2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1)

9. ਓήʔϜͷ‫ج‬ఈͱͳΔಛੑؔ਺
v{1} = (1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1)
v{2} = (0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1)
v{3} = (0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1)
v{4} = (0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1)
v{1,2} = (0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1)
v{1,3} = (0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1)
v{1,4} = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1)
v{2,3} = (0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1)
v{2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1)
v{3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1)
v{1,2,3} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1)
v{1,2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1)
v{1,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1)
v{2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1)
v{1,2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1)
ϕΫτϧද‫ه‬ vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})

10.
v{1} = (1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1)
v{2} = (0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1)
v{3} = (0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1)
v{4} = (0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1)
v{1,2} = (0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1)
v{1,3} = (0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1)
v{1,4} = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1)
v{2,3} = (0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1)
v{2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1)
v{3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1)
v{1,2,3} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1)
v{1,2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1)
v{1,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1)
v{2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1)
v{1,2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1)
vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})
֤ಛੑؔ਺ʹରͯ͠ެཧΛຬͨ͢ ͷ஋
ψ
֤ήʔϜ
ʹ͓͍ͯ
ʹ‫·ؚ‬ΕΔϓϨΠϠʔ͸ରশ
ʹ‫·ؚ‬Εͳ͍ϓϨΠϠʔ͸φϧϓϨΠϠʔ
vR R ⊆ N, R ≠ ∅
R
R

11.
v{1} = (1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1)
v{2} = (0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1)
v{3} = (0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1)
v{4} = (0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1)
v{1,2} = (0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1)
v{1,3} = (0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1)
v{1,4} = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1)
v{2,3} = (0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1)
v{2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1)
v{3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1)
v{1,2,3} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1)
v{1,2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1)
v{1,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1)
v{2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1)
v{1,2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1)
vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})
֤ಛੑؔ਺ʹରͯ͠ެཧΛຬͨ͢ ͷ஋
ψ
֤ήʔϜ
ʹ͓͍ͯ
ʹ‫·ؚ‬ΕΔϓϨΠϠʔ͸ରশ
ʹ‫·ؚ‬Εͳ͍ϓϨΠϠʔ͸φϧϓϨΠϠʔ
vR R ⊆ N, R ≠ ∅
R
R
ψ(v{1}) = (ψ1(v{1}), ψ2(v{1}), ψ3(v{1}), ψ4(v{1})) = (1,0,0,0)
ψ(v{2}) = (0,1,0,0)
ψ(v{3}) = (0,0,1,0)
ψ(v{4}) = (0,0,0,1)
ψ(v{1,2}) =
(
1
2
,
1
2
, 0, 0
)
ψ(v{1,3}) =
(
1
2
, 0,
1
2
, 0
)
ψ(v{1,4}) =
(
1
2
, 0, 0,
1
2)
ψ(v{2,3}) =
(
0,
1
2
,
1
2
, 0
)
ψ(v{2,4}) =
(
0,
1
2
, 0,
1
2)
ψ(v{3,4}) =
(
0, 0,
1
2
,
1
2)
֤ήʔϜ
ʹ͓͍ͯ
ʹ‫·ؚ‬ΕΔϓϨΠϠʔ͸ରশ
ʹ‫·ؚ‬Εͳ͍ϓϨΠϠʔ͸φϧϓϨΠϠʔ
vR R ⊆ N, R ≠ ∅
R
R

12.
ψ(v{1}) = (1,0,0,0)
ψ(v{2}) = (0,1,0,0)
ψ(v{3}) = (0,0,1,0)
ψ(v{4}) = (0,0,0,1)
ψ(v{1,2}) =
(
1
2
,
1
2
, 0, 0
)
ψ(v{1,3}) =
(
1
2
, 0,
1
2
, 0
)
ψ(v{1,4}) =
(
1
2
, 0, 0,
1
2)
ψ(v{2,3}) =
(
0,
1
2
,
1
2
, 0
)
ψ(v{2,4}) =
(
0,
1
2
, 0,
1
2)
ψ(v{3,4}) =
(
0, 0,
1
2
,
1
2)
v{1,2,3} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1)
v{1,2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1)
v{1,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1)
v{2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1)
v{1,2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1)
vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})
֤ಛੑؔ਺ʹରͯ͠ެཧΛຬͨ͢ ͷ஋
ψ
ψ(v{1,2,3}) =
(
1
3
,
1
3
,
1
3
, 0
)
ψ(v{1,2,4}) =
(
1
3
,
1
3
, 0,
1
3)
ψ(v{1,3,4}) =
(
1
3
, 0,
1
3
,
1
3)
ψ(v{2,3,4}) =
(
0,
1
3
,
1
3
,
1
3)
ψ(v{1,2,3,4}) =
(
1
4
,
1
4
,
1
4
,
1
4)
֤ήʔϜ
ʹ͓͍ͯ
ʹ‫·ؚ‬ΕΔϓϨΠϠʔ͸ରশ
ʹ‫·ؚ‬Εͳ͍ϓϨΠϠʔ͸φϧϓϨΠϠʔ
vR R ⊆ N, R ≠ ∅
R
R

13.
ψ(v{1}) = (1,0,0,0)
ψ(v{2}) = (0,1,0,0)
ψ(v{3}) = (0,0,1,0)
ψ(v{4}) = (0,0,0,1)
ψ(v{1,2}) =
(
1
2
,
1
2
, 0, 0
)
ψ(v{1,3}) =
(
1
2
, 0,
1
2
, 0
)
ψ(v{1,4}) =
(
1
2
, 0, 0,
1
2)
ψ(v{2,3}) =
(
0,
1
2
,
1
2
, 0
)
ψ(v{2,4}) =
(
0,
1
2
, 0,
1
2)
ψ(v{3,4}) =
(
0, 0,
1
2
,
1
2)
ψ(v{1,2,3}) =
(
1
3
,
1
3
,
1
3
, 0
)
ψ(v{1,2,4}) =
(
1
3
,
1
3
, 0,
1
3)
ψ(v{1,3,4}) =
(
1
3
, 0,
1
3
,
1
3)
ψ(v{2,3,4}) =
(
0,
1
3
,
1
3
,
1
3)
ψ(v{1,2,3,4}) =
(
1
4
,
1
4
,
1
4
,
1
4)
vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})
֤ಛੑؔ਺ʹରͯ͠ެཧΛຬͨ͢ ͷ஋
ψ

14.
͜ͷήʔϜʹ͓͚ΔγϟʔϓϨΠ஋Λ‫ٻ‬ΊΑ
Ͱ‫ٻ‬Ίͨ஋Λ‫ج‬ఈͱͳΔಛੑؔ਺Λ༻͍ͯಋग़ͤΑ
͜͜Ͱ೚ҙͷಛੑؔ਺͸
֤ಛੑؔ਺ΛϕΫτϧͱΈͳͯ͠
ҎԼͷ‫Ͱܗ‬Ұҙʹද‫͖Ͱݱ‬Δ͜ͱ͸ར༻ͯ͠Α͍
v({1,2,3,4}) = 10 v({1,2,3}) = 6 v({1,2,4}) = 6 v({1,3,4}) = 5 v({2,3,4}) = 5
v({1,2}) = 6 v({1,3}) = 4 v({1,4}) = 4 v({2,3}) = 3 v({2,4}) = 4 v({3,4}) = 3
v({1}) = v({2}) = v({3}) = v({4}) = v(∅) = 0
v = α1v{1} + α2v{2} + α3v{3} + α4v{4} + α12v{1,2} + α13v{1,3} + α14v{1,4} + α23v{2,3} + α24v{2,4} + α34v{3,4}
+α123v{1,2,3} + α124v{1,2,4} + α134v{1,3,4} + α234v{2,3,4} + α1234v{1,2,3,4}
໰୊

15.
͜ͷήʔϜʹ͓͚ΔγϟʔϓϨΠ஋Λ‫ٻ‬ΊΑ
ߩ‫౓ݙ‬ͷ‫ظ‬଴஋Λ‫ٻ‬ΊΕ͹Α͍
v({1,2,3,4}) = 10 v({1,2,3}) = 6 v({1,2,4}) = 6 v({1,3,4}) = 5 v({2,3,4}) = 5
v({1,2}) = 6 v({1,3}) = 4 v({1,4}) = 4 v({2,3}) = 3 v({2,4}) = 4 v({3,4}) = 3
v({1}) = v({2}) = v({3}) = v({4}) = v(∅) = 0
ϕ1(v) =
1
4!
72 =
72
24
= 3
ϕ2(v) =
1
4!
68 =
68
24
=
17
6
ϕ3(v) =
1
4!
48 =
48
24
= 2
ϕ4(v) =
1
4!
52 =
52
24
=
13
6
ϕ(v) =
(
3,
17
6
, 2,
13
6 )
໰୊
ॱྻ

16.
͜ͷήʔϜʹ͓͚ΔγϟʔϓϨΠ஋Λ‫ٻ‬ΊΑ
Λ࢖͏ͷͰ͋Ε͹
ϓϨΠϠʔʹ͍ͭͯ
ͱͯ͠͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
v({1,2,3,4}) = 10 v({1,2,3}) = 6 v({1,2,4}) = 6 v({1,3,4}) = 5 v({2,3,4}) = 5
v({1,2}) = 6 v({1,3}) = 4 v({1,4}) = 4 v({2,3}) = 3 v({2,4}) = 4 v({3,4}) = 3
v({1}) = v({2}) = v({3}) = v({4}) = v(∅) = 0
ϕi(v) =
1
n! ∑
S:S⊆N,i∉S
s!(n − s − 1)!(v(S ∪ {i}) − v(S)), ∀i ∈ N
S : S ⊆ N,1 ∉ S ∅, {2}, {3}, {4}, {2,3}, {2,4}, {3,4}, {2,3,4}
∅ → {1} 0!(4 − 0 − 1)! = 3! = 6
{2} → {1,2} 1!(4 − 1 − 1)! = 2
{3} → {1,3} 1!(4 − 1 − 1)! = 2
{4} → {1,4} 1!(4 − 1 − 1)! = 2
{2,3} → {1,2,3} 2!(4 − 2 − 1)! = 2
{2,4} → {1,2,4} 2!(4 − 2 − 1)! = 2
{3,4} → {1,3,4} 2!(4 − 2 − 1)! = 2
{2,3,4} → {1,2,3,4} 3!(4 − 3 − 1)! = 3! = 6
ϕ1(v) =
1
4!
(6 ⋅ 0 + 2 ⋅ 6 + 2 ⋅ 4 + 2 ⋅ 4 + 2 ⋅ 3 + 2 ⋅ 2 + 2 ⋅ 2 + 6 ⋅ 5) =
1
4!
(0 + 12 + 8 + 8 + 6 + 4 + 4 + 30) =
72
24
= 3
໰୊
ॱྻ

17.
͜ͷήʔϜʹ͓͚ΔγϟʔϓϨΠ஋Λ‫ٻ‬ΊΑ
Λ࢖͏ͷͰ͋Ε͹
ϓϨΠϠʔʹ͍ͭͯ
ͱͯ͠͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
v({1,2,3,4}) = 10 v({1,2,3}) = 6 v({1,2,4}) = 6 v({1,3,4}) = 5 v({2,3,4}) = 5
v({1,2}) = 6 v({1,3}) = 4 v({1,4}) = 4 v({2,3}) = 3 v({2,4}) = 4 v({3,4}) = 3
v({1}) = v({2}) = v({3}) = v({4}) = v(∅) = 0
ϕi(v) =
1
n! ∑
S:S⊆N,i∉S
s!(n − s − 1)!(v(S ∪ {i}) − v(S)), ∀i ∈ N
S : S ⊆ N,2 ∉ S ∅, {1}, {3}, {4}, {1,3}, {1,4}, {3,4}, {1,3,4}
∅ → {2} 0!(4 − 0 − 1)! = 3! = 6
{1} → {1,2} 1!(4 − 1 − 1)! = 2
{3} → {2,3} 1!(4 − 1 − 1)! = 2
{4} → {2,4} 1!(4 − 1 − 1)! = 2
{1,3} → {1,2,3} 2!(4 − 2 − 1)! = 2
{1,4} → {1,2,4} 2!(4 − 2 − 1)! = 2
{3,4} → {2,3,4} 2!(4 − 2 − 1)! = 2
{1,3,4} → {1,2,3,4} 3!(4 − 3 − 1)! = 3! = 6
ϕ1(v) =
1
4!
(6 ⋅ 0 + 2 ⋅ 6 + 2 ⋅ 3 + 2 ⋅ 4 + 2 ⋅ 2 + 2 ⋅ 2 + 2 ⋅ 2 + 6 ⋅ 5) =
1
4!
(0 + 12 + 6 + 8 + 4 + 4 + 4 + 30) =
68
24
=
17
6
໰୊
ॱྻ

18.
͜ͷήʔϜʹ͓͚ΔγϟʔϓϨΠ஋Λ‫ٻ‬ΊΑ
Λ࢖͏ͷͰ͋Ε͹
ϓϨΠϠʔʹ͍ͭͯ
ͱͯ͠͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
v({1,2,3,4}) = 10 v({1,2,3}) = 6 v({1,2,4}) = 6 v({1,3,4}) = 5 v({2,3,4}) = 5
v({1,2}) = 6 v({1,3}) = 4 v({1,4}) = 4 v({2,3}) = 3 v({2,4}) = 4 v({3,4}) = 3
v({1}) = v({2}) = v({3}) = v({4}) = v(∅) = 0
ϕi(v) =
1
n! ∑
S:S⊆N,i∉S
s!(n − s − 1)!(v(S ∪ {i}) − v(S)), ∀i ∈ N
S : S ⊆ N,3 ∉ S ∅, {1}, {2}, {4}, {1,2}, {1,4}, {2,4}, {1,2,4}
∅ → {3} 0!(4 − 0 − 1)! = 3! = 6
{1} → {1,3} 1!(4 − 1 − 1)! = 2
{2} → {2,3} 1!(4 − 1 − 1)! = 2
{4} → {3,4} 1!(4 − 1 − 1)! = 2
{1,2} → {1,2,3} 2!(4 − 2 − 1)! = 2
{1,4} → {1,3,4} 2!(4 − 2 − 1)! = 2
{2,4} → {2,3,4} 2!(4 − 2 − 1)! = 2
{1,2,4} → {1,2,3,4} 3!(4 − 3 − 1)! = 3! = 6
ϕ1(v) =
1
4!
(6 ⋅ 0 + 2 ⋅ 4 + 2 ⋅ 3 + 2 ⋅ 3 + 2 ⋅ 0 + 2 ⋅ 1 + 2 ⋅ 1 + 6 ⋅ 4) =
1
4!
(0 + 8 + 6 + 6 + 0 + 2 + 2 + 24) =
48
24
= 2
໰୊
ॱྻ

19.
͜ͷήʔϜʹ͓͚ΔγϟʔϓϨΠ஋Λ‫ٻ‬ΊΑ
Λ࢖͏ͷͰ͋Ε͹
ϓϨΠϠʔʹ͍ͭͯ
ͱͯ͠͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
ͱͳΔ৔߹ͷ਺͸ ௨Γ
ߩ‫౓ݙ‬͸
v({1,2,3,4}) = 10 v({1,2,3}) = 6 v({1,2,4}) = 6 v({1,3,4}) = 5 v({2,3,4}) = 5
v({1,2}) = 6 v({1,3}) = 4 v({1,4}) = 4 v({2,3}) = 3 v({2,4}) = 4 v({3,4}) = 3
v({1}) = v({2}) = v({3}) = v({4}) = v(∅) = 0
ϕi(v) =
1
n! ∑
S:S⊆N,i∉S
s!(n − s − 1)!(v(S ∪ {i}) − v(S)), ∀i ∈ N
S : S ⊆ N,4 ∉ S ∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}
∅ → {4} 0!(4 − 0 − 1)! = 3! = 6
{1} → {1,4} 1!(4 − 1 − 1)! = 2
{2} → {2,4} 1!(4 − 1 − 1)! = 2
{3} → {3,4} 1!(4 − 1 − 1)! = 2
{1,2} → {1,2,4} 2!(4 − 2 − 1)! = 2
{1,3} → {1,3,4} 2!(4 − 2 − 1)! = 2
{2,3} → {2,3,4} 2!(4 − 2 − 1)! = 2
{1,2,3} → {1,2,3,4} 3!(4 − 3 − 1)! = 3! = 6
ϕ1(v) =
1
4!
(6 ⋅ 0 + 2 ⋅ 4 + 2 ⋅ 4 + 2 ⋅ 3 + 2 ⋅ 0 + 2 ⋅ 1 + 2 ⋅ 2 + 6 ⋅ 4) =
1
4!
(0 + 8 + 8 + 6 + 0 + 2 + 4 + 24) =
52
24
=
13
6
໰୊
ॱྻ

20. ͕ҎԼͷ‫͚ॻͰܗ‬ΔͷͰ
֤܎਺Λ‫ݩ‬ͷήʔϜʹ͓͚Δಛੑؔ਺ͷ஋Ͱද‫͢ݱ‬Δ
͜ͷϕΫτϧͷཁૉ໨͸ ʹର͢Δಛੑؔ਺஋Ͱ͋Δ͔Β
ಉ༷ʹ
͕‫͑ݴ‬Δ
v
v = α1v{1} + α2v{2} + α3v{3} + α4v{4}
+α12v{1,2} + α13v{1,3} + α14v{1,4} + α23v{2,3} + α24v{2,4} + α34v{3,4}
+α123v{1,2,3} + α124v{1,2,4} + α134v{1,3,4} + α234v{2,3,4} + α1234v{1,2,3,4}
= (α1, α2, α3, α4,
α1 + α2 + α12, α1 + α3 + α13, α1 + α4 + α14, α2 + α3 + α23, α2 + α4 + α24, α3 + α4 + α34
α1 + α2 + α3 + α12 + α13 + α23 + α123, α1 + α2 + α4 + α12 + α14 + α24 + α124
α1 + α3 + α4 + α13 + α14 + α34 + α134, α2 + α3 + α4 + α23 + α24 + α34 + α234
α1 + α2 + α3 + α4 + α12 + α13 + α14 + α23 + α24 + α34 + α123 + α124 + α134 + α234 + α1234)
{1}
α1 = v({1}) = 0
α2 = v({2}) = 0 α3 = v({3}) = 0 α4 = v({4}) = 0
໰୊
v{1} = (1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1)
v{2} = (0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1)
v{3} = (0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1)
v{4} = (0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1)
v{1,2} = (0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1)
v{1,3} = (0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1)
v{1,4} = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1)
v{2,3} = (0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1)
v{2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1)
v{3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1)
v{1,2,3} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1)
v{1,2,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1)
v{1,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1)
v{2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1)
v{1,2,3,4} = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1)
vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})

21.
͜ͷϕΫτϧͷཁૉ໨͸ ʹର͢Δಛੑؔ਺஋Ͱ͋Δ͔Β
ಉ༷ʹ
v = (0, 0, 0, 0,
α12, α13, α14, α23, α24, α34
α12 + α13 + α23 + α123, α12 + α14 + α24 + α124
α13 + α14 + α34 + α134, α23 + α24 + α34 + α234
α12 + α13 + α14 + α23 + α24 + α34 + α123 + α124 + α134 + α234 + α1234)
{1,2}
α1 + α2 + α12 = v({1,2}) ⇔ α12 = v({1,2}) − α1 − α2 ⇔ α12 = 6
α13 = 4 α14 = 4 α23 = 3 α24 = 4 α34 = 3
໰୊
v({1,2,3,4}) = 10 v({1,2,3}) = 6 v({1,2,4}) = 6 v({1,3,4}) = 5 v({2,3,4}) = 5
v({1,2}) = 6 v({1,3}) = 4 v({1,4}) = 4 v({2,3}) = 3 v({2,4}) = 4 v({3,4}) = 3
v({1}) = v({2}) = v({3}) = v({4}) = v(∅) = 0
vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})

22.
͜ͷϕΫτϧͷཁૉ໨͸ ʹର͢Δಛੑؔ਺஋Ͱ͋Δ͔Β
ಉ༷ʹ
v = (0, 0, 0, 0,
6, 4, 4, 3, 4, 3
13 + α123, 14 + α124
11 + α134, 10 + α234
24 + α123 + α124 + α134 + α234 + α1234)
{1,2,3}
13 + α123 = v({1,2,3}) ⇔ α123 = v({1,2,3}) − 13 ⇔ α123 = − 7
α124 = − 8 α134 = − 6 α234 = − 5
໰୊
v({1,2,3,4}) = 10 v({1,2,3}) = 6 v({1,2,4}) = 6 v({1,3,4}) = 5 v({2,3,4}) = 5
v({1,2}) = 6 v({1,3}) = 4 v({1,4}) = 4 v({2,3}) = 3 v({2,4}) = 4 v({3,4}) = 3
v({1}) = v({2}) = v({3}) = v({4}) = v(∅) = 0
vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})

23.
͜ͷϕΫτϧͷཁૉ໨͸ ʹର͢Δಛੑؔ਺஋Ͱ͋Δ͔Β
Ҏ্ΑΓ
v = (0, 0, 0, 0,
6, 4, 4, 3, 4, 3
6, 6
5, 5
−2 + α1234)
{1,2,3,4}
−2 + α1234 = v({1,2,3,4}) ⇔ α1234 = v({1,2,3,4}) + 2 ⇔ α1234 = 12
v = 0v{1} + 0v{2} + 0v{3} + 0v{4}
+6v{1,2} + 4v{1,3} + 4v{1,4} + 3v{2,3} + 4v{2,4} + 3v{3,4}
−7v{1,2,3} − 8v{1,2,4} − 6v{1,3,4} − 5v{2,3,4} + 12v{1,2,3,4}
໰୊
v({1,2,3,4}) = 10 v({1,2,3}) = 6 v({1,2,4}) = 6 v({1,3,4}) = 5 v({2,3,4}) = 5
v({1,2}) = 6 v({1,3}) = 4 v({1,4}) = 4 v({2,3}) = 3 v({2,4}) = 4 v({3,4}) = 3
v({1}) = v({2}) = v({3}) = v({4}) = v(∅) = 0
vR = (x{1}, x{2}, x{3}, x{4}, x{1,2}, x{1,3}, x{1,4}, x{2,3}, x{2,4}, x{3,4}, x{1,2,3}, x{1,2,4}, x{1,3,4}, x{2,3,4}, x{1,2,3,4})

24.
Ճ๏ੑΑΓ
v = 0v{1} + 0v{2} + 0v{3} + 0v{4}+6v{1,2} + 4v{1,3} + 4v{1,4} + 3v{2,3} + 4v{2,4} + 3v{3,4}
−7v{1,2,3} − 8v{1,2,4} − 6v{1,3,4} − 5v{2,3,4} + 12v{1,2,3,4}
v + 7v{1,2,3} + 8v{1,2,4} + 6v{1,3,4} + 5v{2,3,4} = 6v{1,2} + 4v{1,3} + 4v{1,4} + 3v{2,3} + 4v{2,4} + 3v{3,4} + 12v{1,2,3,4}
ψ(v + 7v{1,2,3} + 8v{1,2,4} + 6v{1,3,4} + 5v{2,3,4}) = ψ(6v{1,2} + 4v{1,3} + 4v{1,4} + 3v{2,3} + 4v{2,4} + 3v{3,4} + 12v{1,2,3,4})
⇔ ψ(v) + 7ψ(v{1,2,3}) + 8ψ(v{1,2,4}) + 6ψ(v{1,3,4}) + 5ψ(v{2,3,4}) = 6ψ(v{1,2}) + 4ψ(v{1,3}) + 4ψ(v{1,4}) + 3ψ(v{2,3}) + 4ψ(v{2,4}) + 3ψ(v{3,4}) + 12ψ(v{1,2,3,4})
⇔ ψ(v) + 7
(
1
3
,
1
3
,
1
3
, 0
)
+ 8
(
1
3
,
1
3
, 0,
1
3)
+ 6
(
1
3
, 0,
1
3
,
1
3 )
+ 5
(
0,
1
3
,
1
3
,
1
3)
= 6
(
1
2
,
1
2
, 0, 0
)
+ 4
(
1
2
, 0,
1
2
, 0
)
+ 4
(
1
2
, 0, 0,
1
2)
+ 3
(
0,
1
2
,
1
2
, 0
)
+ 4
(
0,
1
2
, 0,
1
2)
+ 3
(
0, 0,
1
2
,
1
2)
+ 12
(
1
4
,
1
4
,
1
4
,
1
4)
⇔ ψ(v) +
(
7,
20
3
, 6,
19
3 )
=
(
10,
19
2
, 8,
17
2 )
⇔ ψ(v) =
(
3,
17
6
, 2,
13
6 )
໰୊
ψ(v{1,2}) =
(
1
2
,
1
2
, 0, 0
)
ψ(v{1,3}) =
(
1
2
, 0,
1
2
, 0
)
ψ(v{1,4}) =
(
1
2
, 0, 0,
1
2)
ψ(v{2,3}) =
(
0,
1
2
,
1
2
, 0
)
ψ(v{2,4}) =
(
0,
1
2
, 0,
1
2)
ψ(v{3,4}) =
(
0, 0,
1
2
,
1
2)
ψ(v{1,2,3}) =
(
1
3
,
1
3
,
1
3
, 0
)
ψ(v{1,2,4}) =
(
1
3
,
1
3
, 0,
1
3)
ψ(v{1,3,4}) =
(
1
3
, 0,
1
3
,
1
3)
ψ(v{2,3,4}) =
(
0,
1
3
,
1
3
,
1
3)
ψ(v{1,2,3,4}) =
(
1
4
,
1
4
,
1
4
,
1
4)

25. ήʔϜཧ࿦#4*$ԋश
ਓήʔϜͷγϟʔϓϨΠ஋Λ‫ٻ‬ΊΔ
࣍ճɿԋश