The document provides a comprehensive overview of artificial neural networks (ANNs), detailing their structure, including input, hidden, and output layers, as well as training methodologies such as supervised and unsupervised learning. It discusses the optimization of connection weights through various methods like backpropagation and criteria for determining the number of hidden nodes and layers. Additionally, it references the use of specific R software packages for implementing ANN and offers guidelines for fine-tuning and optimizing the network.

1. ARTIFICIAL NEURAL
NETWORKS
CLASSIFICATION

2. DEFINITION OF NEURAL NETWORK
 An artificial neural network (ANN) is a parallel
connection of a set of nodes called neurons.
 From the statistical viewpoint, it represents a
function of explanatory variables which is
composed of simple building blocks and which
may be used to provide an approximation of
conditional expectations or, in particular,
probabilities in regression or classification.

3. ANN WITH AN INPUT
LAYER, ONE HIDDEN LAYER AND AN OUTPUT LAYER
I1
I2
I3
I4
Sepal.Length
Sepal.Width
Petal.Length
Petal.Width
H1
H2
O1
O2
O3
setosa
versicolor
virginica
B1 B2

4. DEFINITION OF THE ANN
 In this study, we only consider:
 A feed-forward net with d + 1 input nodes,
 One layer of H hidden nodes,
 C output nodes ,
 An activation function
 The input and hidden layer nodes are connected by
weights Whj for
and
 The hidden and output layers are connected by
weights for
and
 
H
h ,...,
1

 
d
j ,...,
0

ch

 
H
h ,...,
1

 
C
c ,...,
1

)
(x


5. TRAINING THE NETWORK
 The connection weights are adjusted through
training.
 There exists two training paradigms: Non
supervised and supervised learning.
 We discuss and later apply supervised learning.

6. REQUIREMENTS FOR SUPERVISED TRAINING
 A sample of d input vectors, of size
n each,
 An associated output vector,
of size n,
 The selection of an initial weight set.
 A repetitive method to update the current weights to
optimize the input-output map.
 A stopping rule.
d
X
X
X ,...,
1

C
Y
Y
Y ,...,
1


7. A REPETITIVE METHOD TO UPDATE THE CURRENT
WEIGHTS TO OPTIMIZE THE INPUT-OUTPUT MAP
 Error Function
 The maximum likelihood method is used to
determine the error function.
 The error function is then used to train a given
network.
 
2
1
)
;
(
)
;
,
( 



n
i
i
i X
Z
Y
X
Y
S 


8. UPDATING THE WEIGHTS
 This step involves updating the weights until the error
function is minimized.
 There are various methods
of minimizing namely:
(1) Backpropagation (BP)
(2) The Quasi-Newton method
(3) Broyden–Fletcher–Goldfarb–Shanno (BFGS)
method
(4) The Simulated Annealing method
)
;
,
( 
X
Y
S
)
;
,
( 
X
Y
S

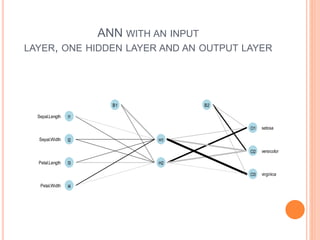
9. NUMBER OF HIDDEN LAYERS
 A neural net can have more than one hidden layer,
see Looney [1] for more details.
 However, it is shown in White [2] that one hidden
layer with sufficient number of neurons is enough
to approximate any function of interest.
 In practice, however, a network with more than
one layer may provide a more parsimonious
model for the data.
 The number of neurodes, H, in the hidden layer can
be determined as in Looney [2] by a rule of thumb:
1
)
(
log
*
7
.
1 2 
 n
H

10. NUMBER OF HIDDEN LAYERS
 Alternatively, one can use the Black Information
Criterion (BIC) as proposed in Swanson and White
[3] to sequentially determine H.

11. STOPPING RULES
There are four common stopping rules:
(1)
(2)
(3) a pre-specified lower bound
for the training error
(4) where MAX is the pre-specified
number of iterations.
We note that Rule(4) can be used together with
Rule(1), Rule(2) or Rule(3).
0
)
(
)
1
(





 for
Q
Q r
r
small
but
for
Q
X
Y
S
Q
X
Y
S r
r
0
)
ˆ
;
,
(
)
ˆ
;
,
( )
(
)
1
(






min
)
(
)
ˆ
;
,
( E
Q
X
Y
S r

MAX
r 

12. NNET IN R
They are many packages for ANN. We will use the nnet
package that comes with standard R software.
Run the provided Artificial Neural Net R program. Make
sure you understand each and every step.
Fine tune the program based on:
 Number of hidden nodes
 Important Variables

13. EXERCISE
OPTIMIZE THE NETWORK ON THE NUMBER OF
HIDDEN NODES AS INFORMED BY THE AIC
Y – AXIS  AIC
X-AXIS  NUMBER OF HIDDEN NODES
Hint: You may use the for loop

14. REFRENCES
(1) Looney, C. G. Pattern recognition using neural
networks: theory and algorithms for engineers and
scientists. Oxford University Press,Newyork, 1997.
(2) White, H. “Some asymptotic results for learning in single
hiddenlayer feedforward network models” [J. Amer.
Statist. Assoc. 84 (1989), no. 408, 1003–1013;
MR1134490 (92e:62119)]. J. Amer. Statist. Assoc.
87, 420 (1992), 1252.

15. REFERENCES
(3) Swanson, N. R., and White, H. A model-selection
approach to assessing the information in the term
structure using linear models and artificial neural
networks. J. Bus. Econom. Statist. 13, 3 (1995),
265 – 275.