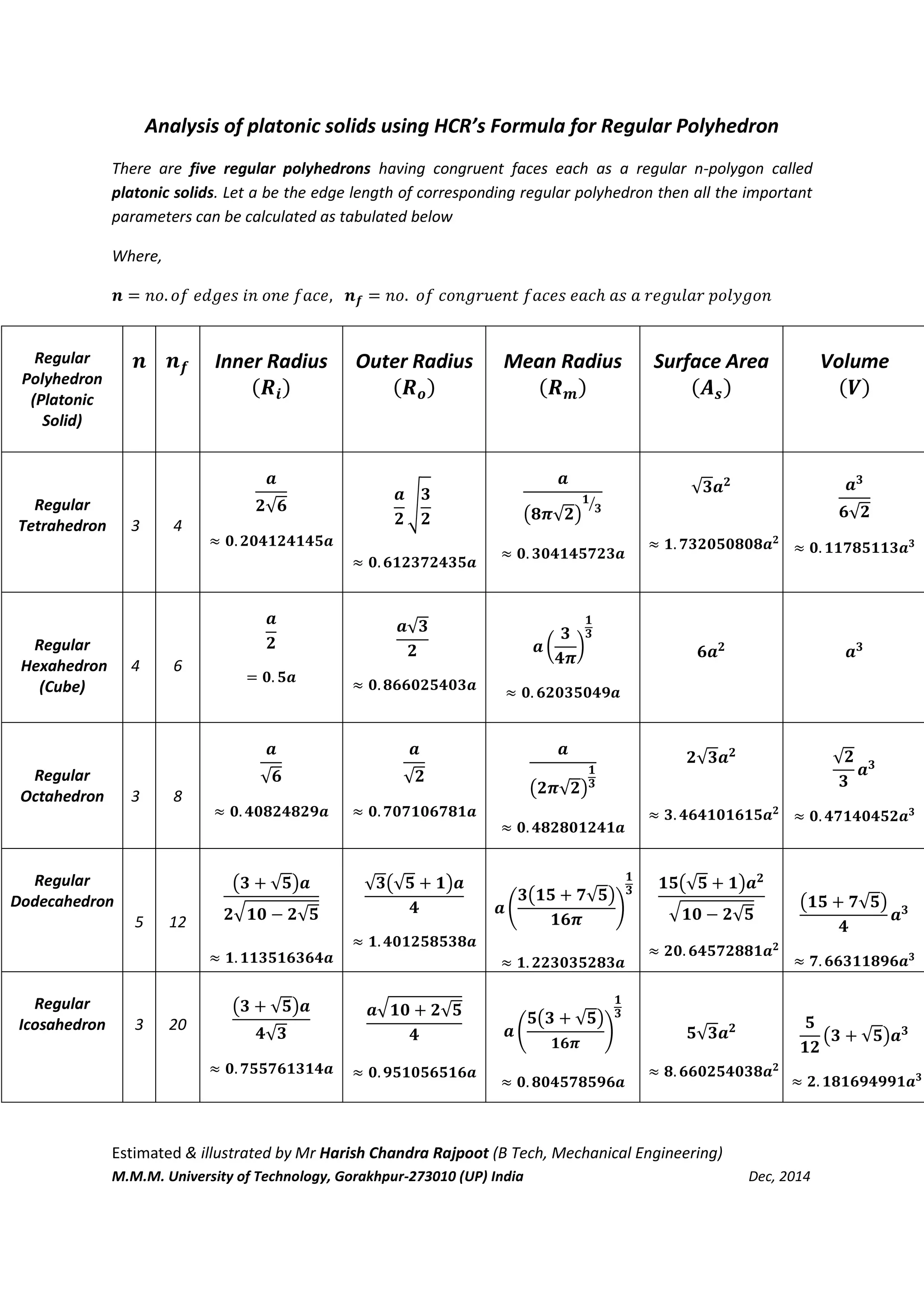
There are five regular polyhedrons called platonic solids that have congruent faces of regular polygons. The document lists these five solids and provides a table calculating their inner radius, outer radius, mean radius, surface area, and volume based on their edge length. The calculations are attributed to Harish Chandra Rajpoot.

1. Analysis of platonic solids using HCR’s Formula for Regular Polyhedron
There are five regular polyhedrons having congruent faces each as a regular n-polygon called platonic solids. Let a be the edge length of corresponding regular polyhedron then all the important parameters can be calculated as tabulated below
Where,
Regular Polyhedron
(Platonic Solid)
Inner Radius ( )
Outer Radius ( )
Mean Radius ( )
Surface Area ( )
Volume ( )
Regular
Tetrahedron
3
4
√
√
( √ ) ⁄
√
√
Regular
Hexahedron (Cube)
4
6
√
( )
Regular Octahedron
3
8
√
√
( √ )
√
√
Regular Dodecahedron
5
12
( √ ) √ √
√ (√ )
( ( √ ) )
(√ ) √ √
( √ )
Regular Icosahedron
3
20
( √ ) √
√ √
( ( √ ) )
√
( √ )
Estimated & illustrated by Mr Harish Chandra Rajpoot (B Tech, Mechanical Engineering) M.M.M. University of Technology, Gorakhpur-273010 (UP) India Dec, 2014