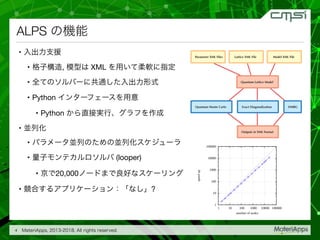
1. ALPS (Applications and Libraries for Physics Simulations) is an open source software project that provides a framework for large-scale simulations of quantum many-body systems using quantum Monte Carlo and other numerical techniques. 2. It contains libraries and applications for lattice models, quantum lattice models, and other physics simulations. Models can be defined through XML files and simulations run using the simplemc program. 3. Results such as magnetization and specific heat are output in XML format and can be analyzed using the Python analysis module or visualized using ParaView.

1. /
MateriApps
CCMS
MateriApps LIVE
ALPS
2018-08-28

2. ALPS (Applications and Libraries for Physics Simulations)
•
•
• ( , , , etc)
• , , , …
•
• , , ,
(DMRG), (DMFT)
•
•
• ( , )
2
H =
Jxy
2
⟨i,j⟩
(S+
i S−
j + S−
i S+
j ) + Jz
⟨i,j⟩
Sz
i Sz
j

3. ALPS
• 500 ALPS ( 2014 7 )
• Nonequilibrium dynamical cluster theory
• Reliability evaluation of thermophysical properties from first-principles
calculations
• Phase diagram study of a dimerized spin-S zig–zag ladder
• First order dynamical phase transitions
• Magnetic transitions in the spin-5/2 frustrated magnet BiMn2PO6 and strong
lattice softening in BiMn2PO6 and BiZn2PO6 below 200 K
• GPU-based simulation of the long-range Potts model via parallel tempering
• Quasi-two-dimensional S=1/2 magnetism of Cu[C6H2(COO)4][C2H5NH3]2
• Exploring unconventional Hubbard models with doubly-modulated lattice gases
• The sign problem in full configuration interaction quantum Monte Carlo: Linear
and sub-linear representation regimes for the exact wave function
…
3
http://alps.comp-phys.org/mediawiki/index.php/PapersTalks

4. ALPS
•
• , XML
•
• Python
• Python
•
•
• (looper)
• 20,000
• ?
4
1
10
100
1000
10000
100000
1 10 100 1000 10000 100000
speedup
number of nodes
Parameter XML Files
Outputs in XML Format
Quantum Lattice Model
Quantum Monte Carlo Exact Diagonalization DMRG
Lattice XML File Model XML File

5. (1)
1.
•
• ( Tc=2.269… )
• (T > Tc):
• (T < Tc):
• ( )
• ( )
2. ( )
•
5
H = J
X
hi,ji
i j ( = ±1)

6. (2)
3. XY
•
(Kosterlitz-Thouless )
•
4.
• =
• (120 )
• 3 1
•
6
H = J
X
hi,ji
Sx
i Sx
j + Sy
i Sy
j ((Sx
i )2
+ (Sy
i )2
= 1)

7. • simplemc :
• Accessories LXTerminal
• ( Italic )
• cd
• cp -r /usr/share/alps/tutorials/mc-09-snapshot .
• cd mc-09-snapshot
• ( XML parm9a.*.in.xml )
• parameter2xml parm9a
•
• simplemc parm9a.in.xml
•
• python plot9a.py
• (3 )
7

8. (parm9a)
8
LATTICE="square lattice"
J=1
ALGORITHM="ising"
SWEEPS=65536
L=8
{ T=5.0 }
{ T=4.5 }
{ T=4.0 }
{ T=3.5 }
{ T=3.0 }
{ T=2.9 }
{ T=2.8 }
{ T=2.7 }
…
(J>0)
(L=8, 16, 24)
( XML (*.task*.*) )

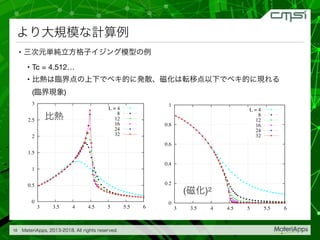
9. (plot9a.py)
• Python
•
•
• matplotlib
9
data = pyalps.loadMeasurements(pyalps.getResultFiles(prefix='parm9a'),
['Specific Heat', 'Magnetization Density^2', 'Binder Ratio of Magnetization'])
for item in pyalps.flatten(data):
item.props['L'] = int(item.props['L'])
magnetization2 = pyalps.collectXY(data, x='T', y='Magnetization Density^2’,
foreach=['L'])
magnetization2.sort(key=lambda item: item.props['L'])
pyplot.figure()
alpsplot.plot(magnetization2)
pyplot.xlabel('Temperture $T$')
pyplot.ylabel('Magnetization Density Squared $m^2$')
pyplot.legend(loc='best')

10. •
• Tc = 4.512…
•
( )
10
( )2
0
0.2
0.4
0.6
0.8
1
3 3.5 4 4.5 5 5.5 6
L = 4
8
12
16
24
32
0
0.5
1
1.5
2
2.5
3
3 3.5 4 4.5 5 5.5 6
L = 4
8
12
16
24
32

11. ( )
• (parm9b)
• SNAPSHOT_INTERVAL
• SNAPSHOT_INTERVAL
(*.snap)
•
• parameter2xml parm9b
• simplemc parm9b.in.xml
• ls -l parm9b.*.snap
• (*.snap *.vtk)
• snap2vtk parm9b.*.snap
• ls -l parm9b.*.vtk
• VTK (±1)
11
LATTICE="square lattice"
J=1
ALGORITHM="ising"
SWEEPS=16384
THERMALIZATION=0
SNAPSHOT_INTERVAL=16384
L = 128
{ T = 3.0 }
{ T = 2.3 }
{ T = 2.0 }

12. ParaView
• paraview
• file open parm9b.task1.clone1.16384.vtk OK Apply
• filters common glyph ( )
• Glyph Type = Box, X Length = 0.08, Y Length = 0.08, Glyph Mode = All Points
Apply
• +z
• OpenGL window
• file open parm9b.task2.clone1.16384.vtk OK Apply
• filters common glyph ( )
• Glyph
12

13. ParaView ( )
• OpenGL window
• file open parm9b.task3.clone1.16384.vtk OK Apply
• filters common glyph ( )
• Glyph
•
•
• Tools Add Camera Link
• ( Link Camera...
)
•
13

14. 14
F = E TS
T=0.995Tc T=Tc T=1.05Tc
ordered state disordered state
critical point

15. XY
•
• parameter2xml parm9c
• simplemc parm9c.in.xml
• snap2vtk parm9c.*.snap
• ParaView
• paraview
• file open
parm9c.task1.clone1.16384.vtk OK
• properties Apply
• Glyph
• Glyph Type = 2D Glyph, Glyph Type = Arrow, Scale Factor = 1, Glyph Mode = All
Points Apply
15
LATTICE="square lattice"
J=1
ALGORITHM="xy"
SWEEPS=16384
THERMALIZATION=0
SNAPSHOT_INTERVAL=16384
L = 64
{ T = 0.01 }

16. •
• parameter2xml parm9d
• simplemc parm9d.in.xml
• snap2vtk parm9d.*.snap
• ParaView
• paraview
• file open
parm9d.task1.clone1.16384.vtk OK
• properties Apply
• Glyph Arrow
• Display Color by Glyph Vector Z Properties
• (parm9d.task2.clone1.16384.vtk)
16
LATTICE="triangular lattice"
J=-1
ALGORITHM="heisenberg"
SWEEPS=16384
THERMALIZATION=0
SNAPSHOT_INTERVAL=16384
L = 48
T = 0.01
{ H = 0 }
{ H = 5 }

17. • ALPS
• “ ” ALPS
, 70, 275 (2015) [https://www.jps.or.jp/books/gakkaishi/2015/04/
06/70-04exp.pdf]
• ALPS web
• http://exa.phys.s.u-tokyo.ac.jp/archive/ma.cms-initiative.jp/ja/listapps/alps/
ju6d5o/llgd83.html
• ALPS
• https://github.com/cmsi/alps-tutorial/releases/tag/20170720
• ALPS Tutorials
• http://alps.comp-phys.org/mediawiki/index.php/ALPS_2_Tutorials:Overview/ja
17