Downloaded 15 times
Uploaded byAlois Reitbauer
The Dark of Building an Production Incident Syste
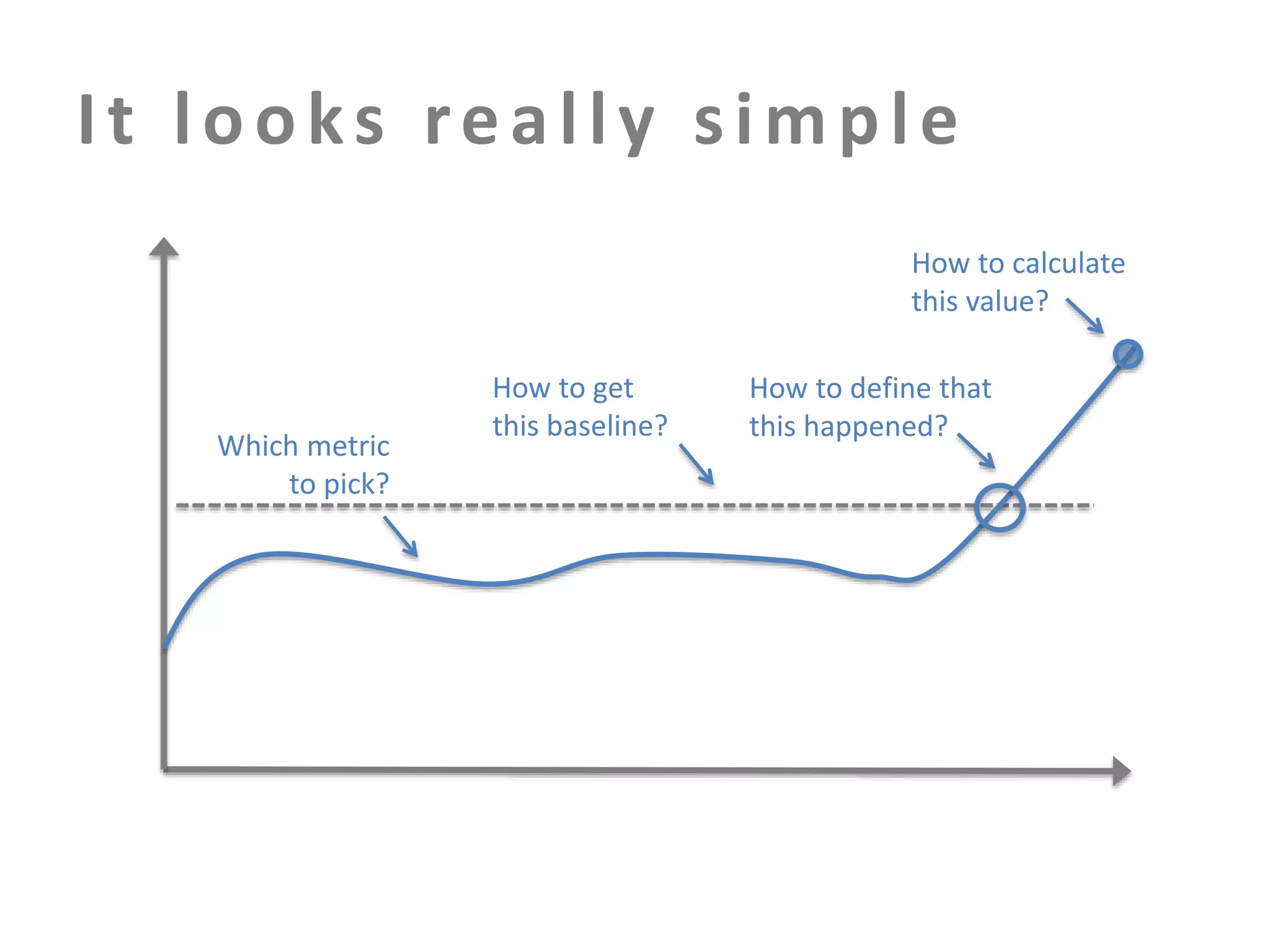
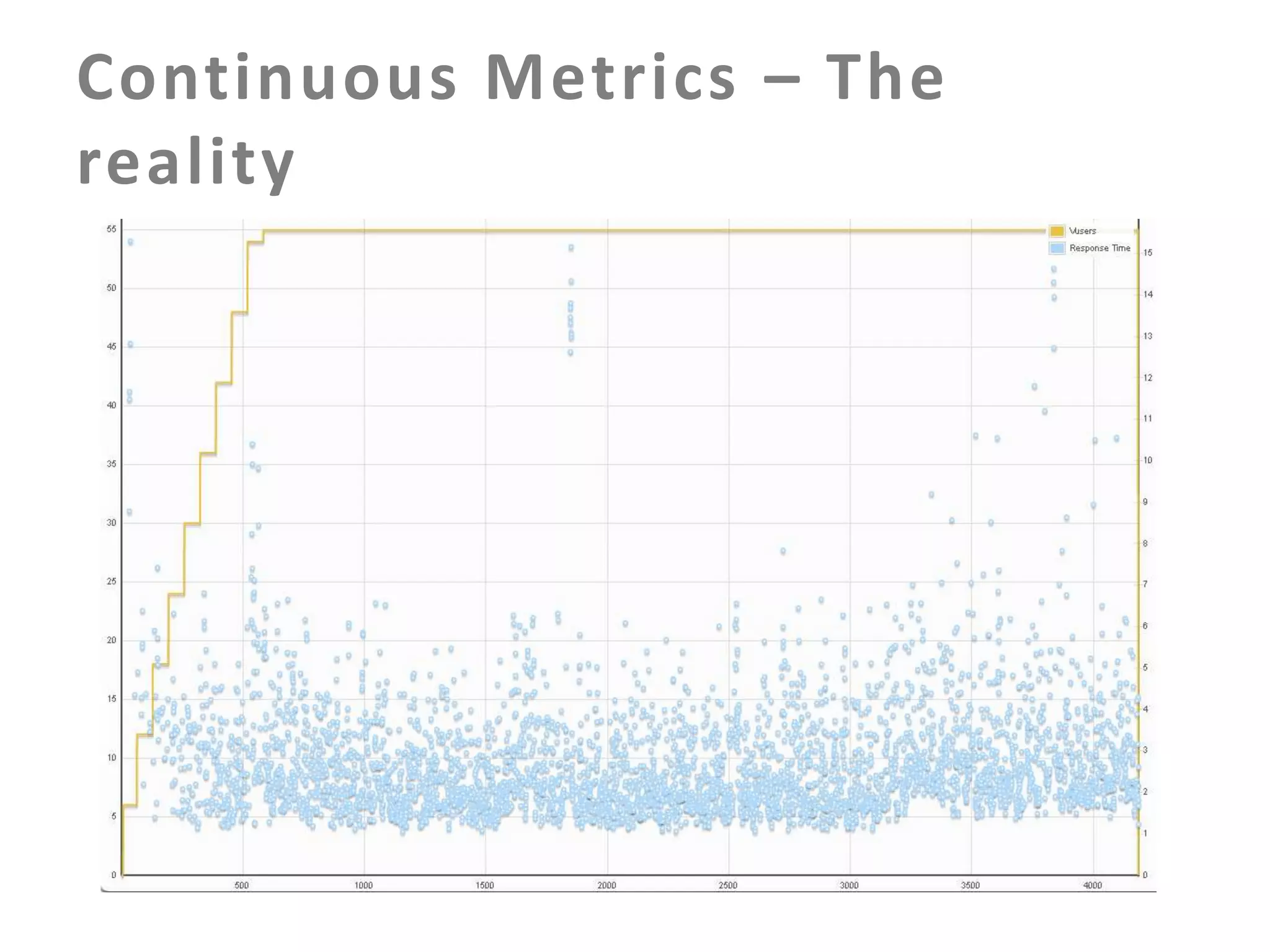
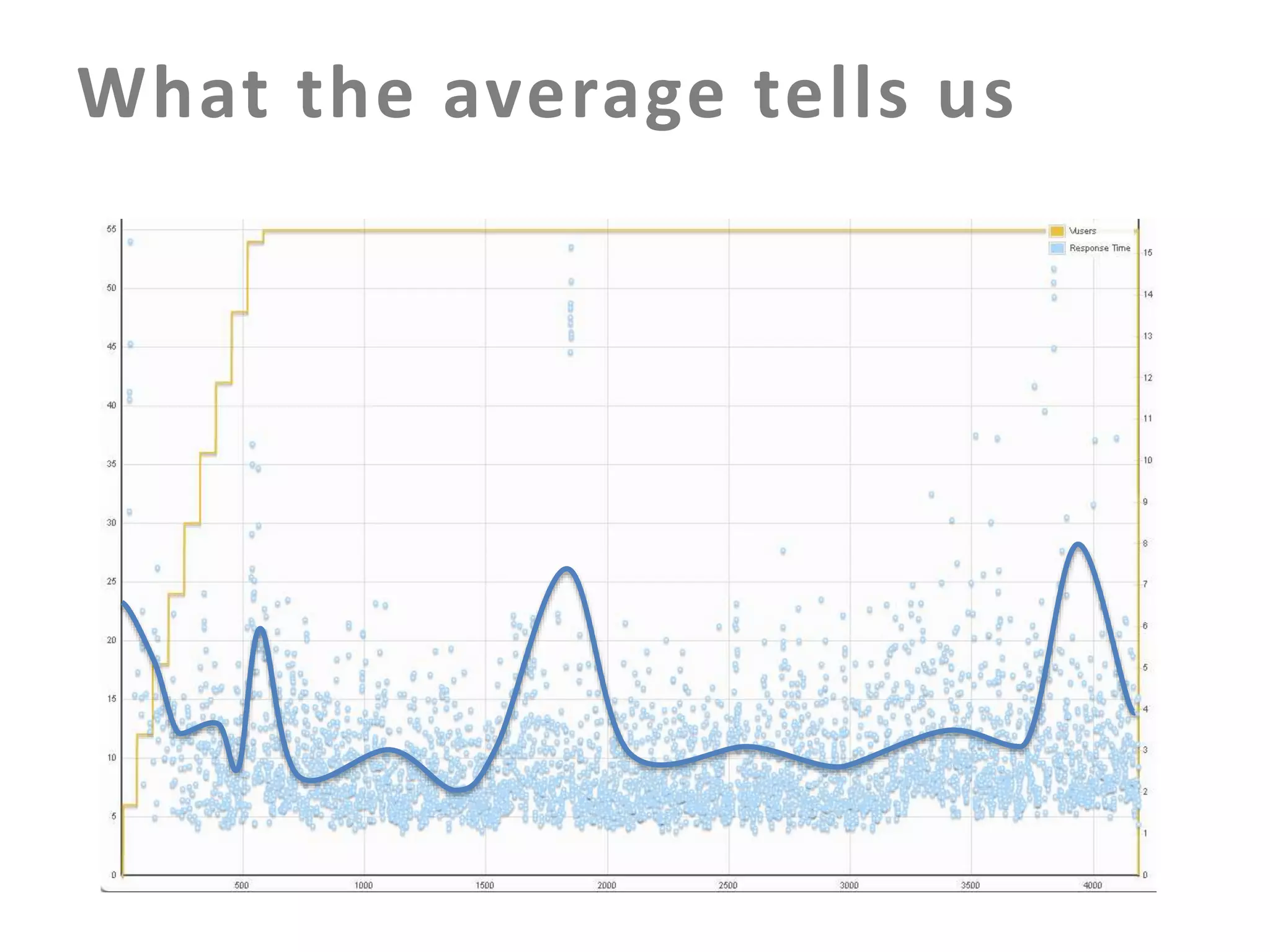
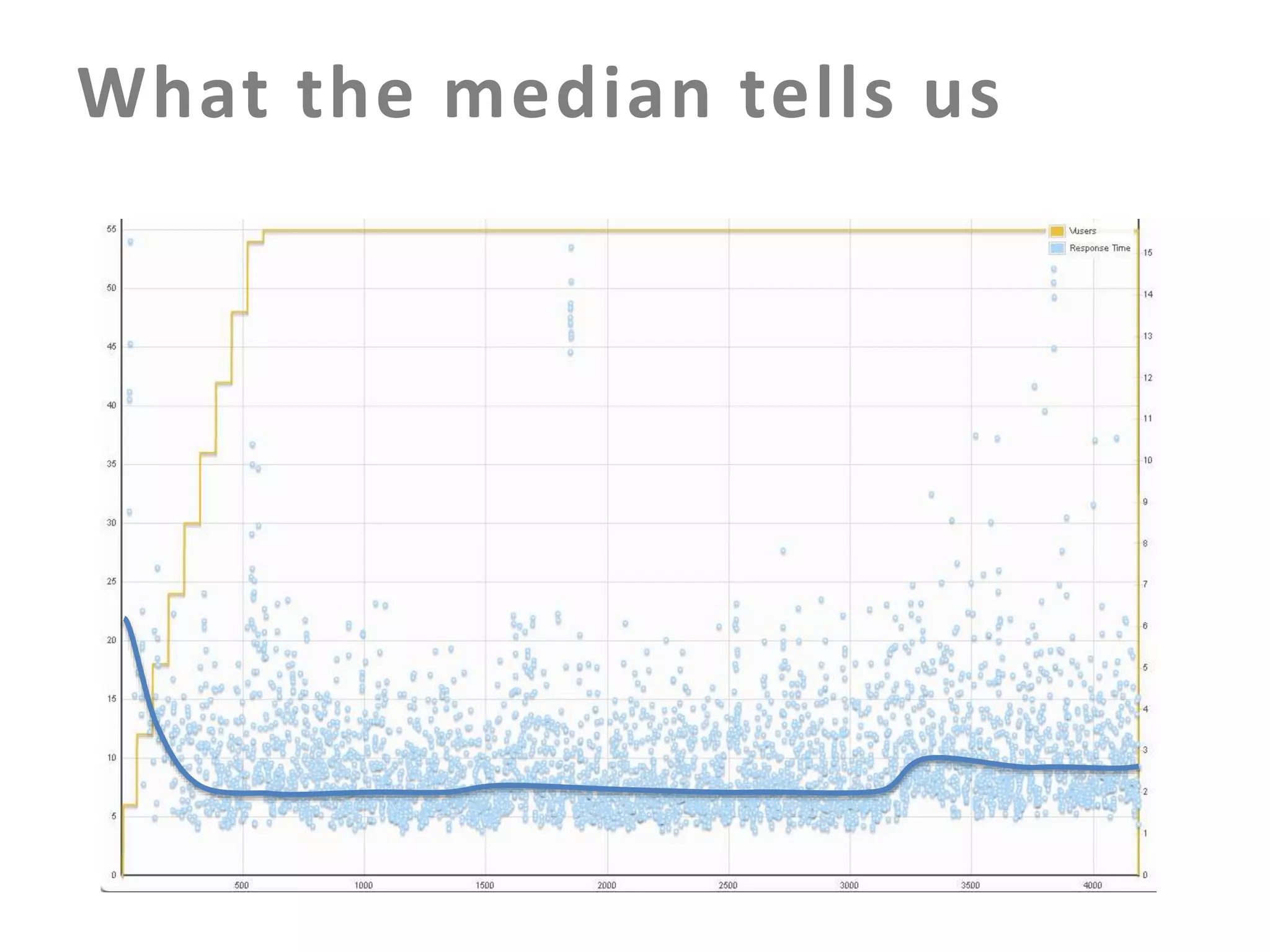
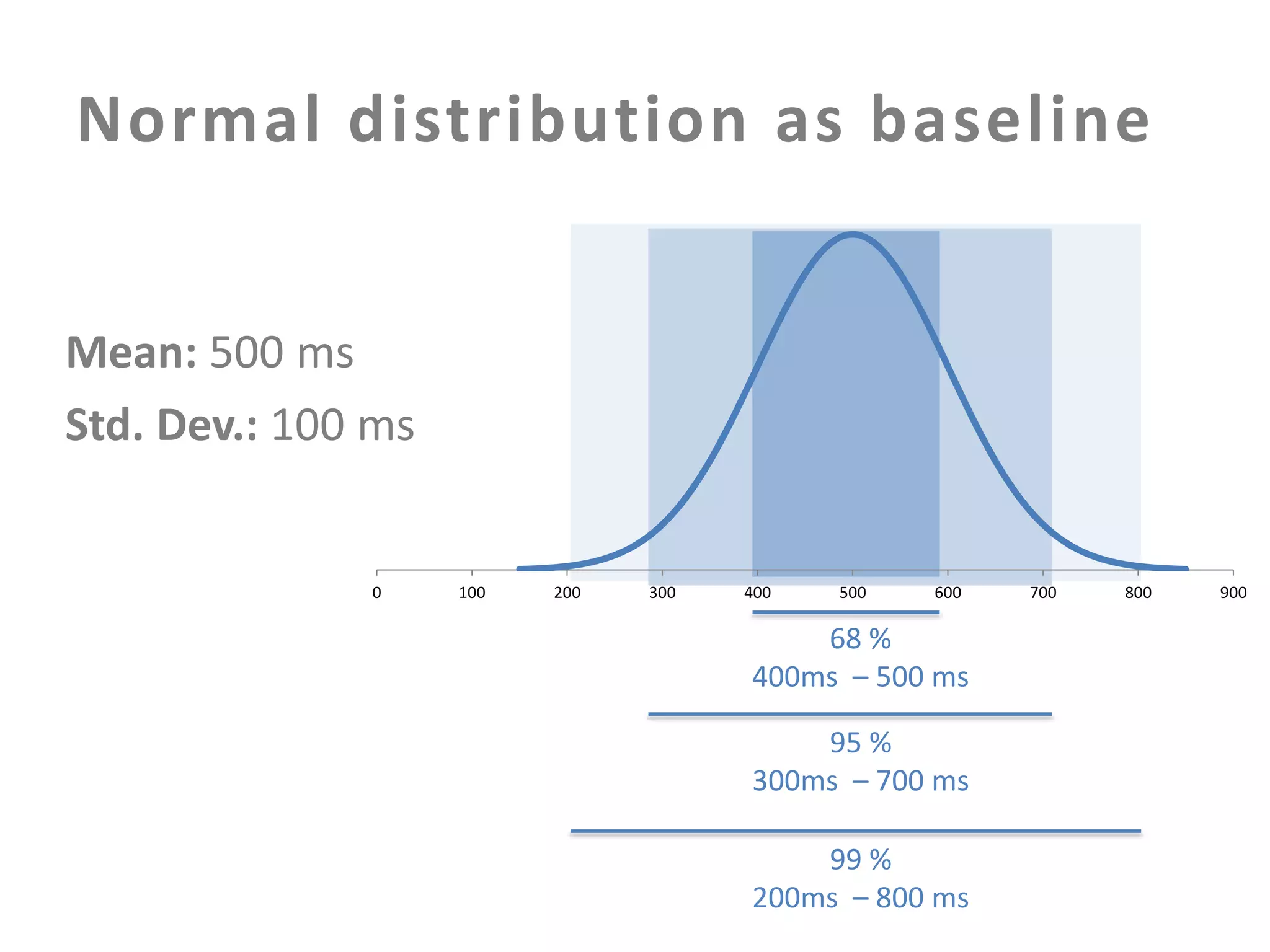
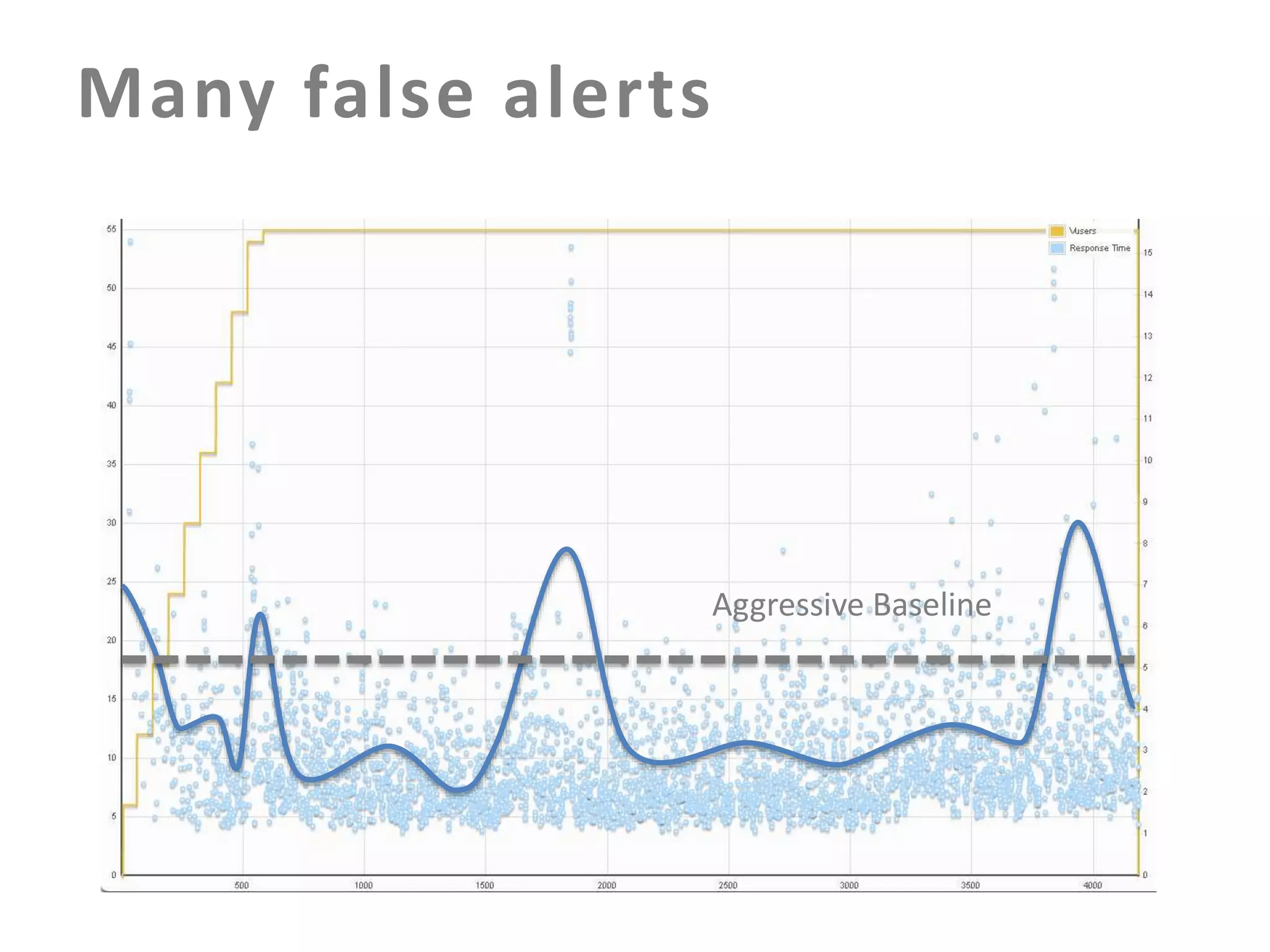
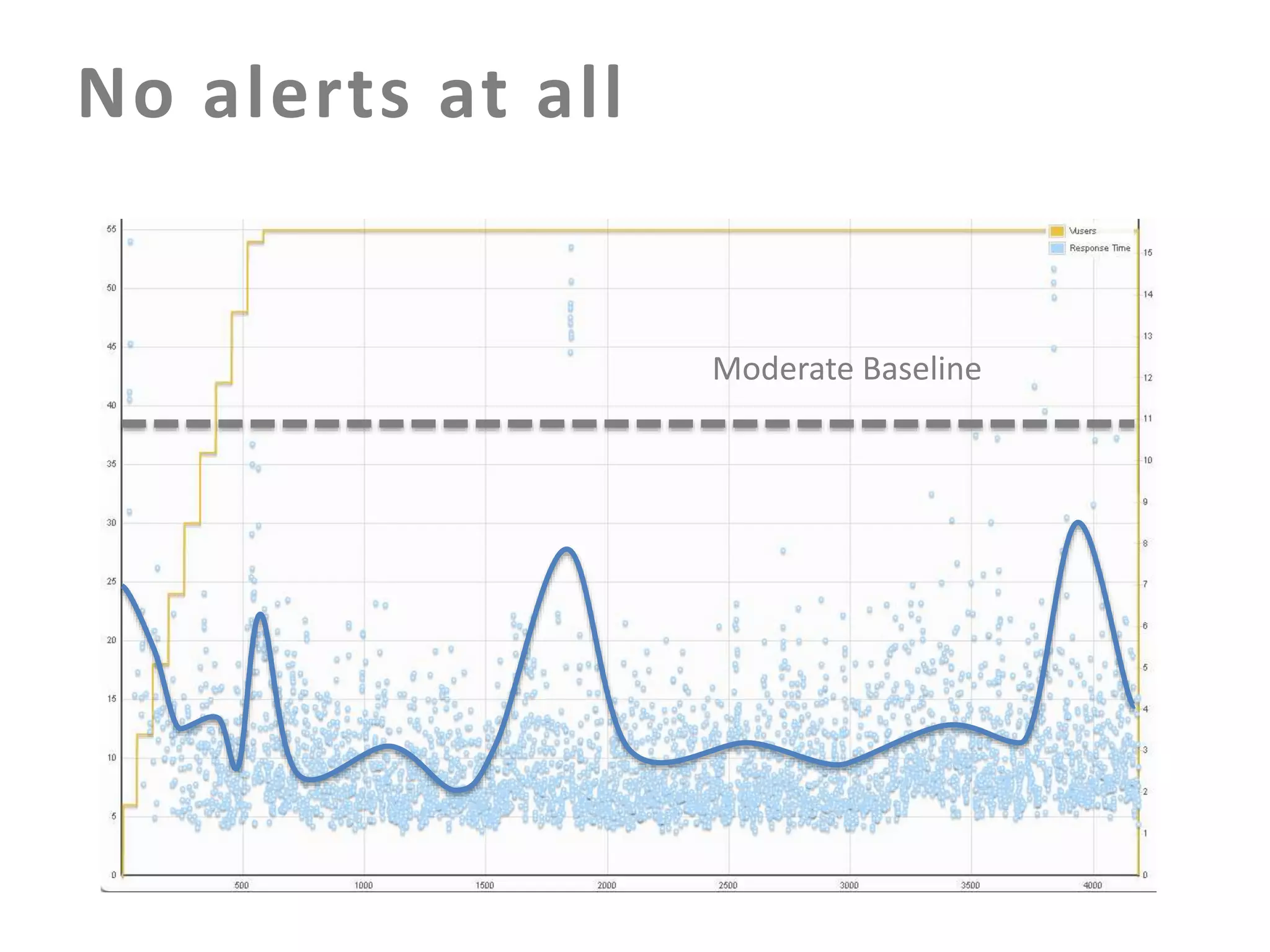
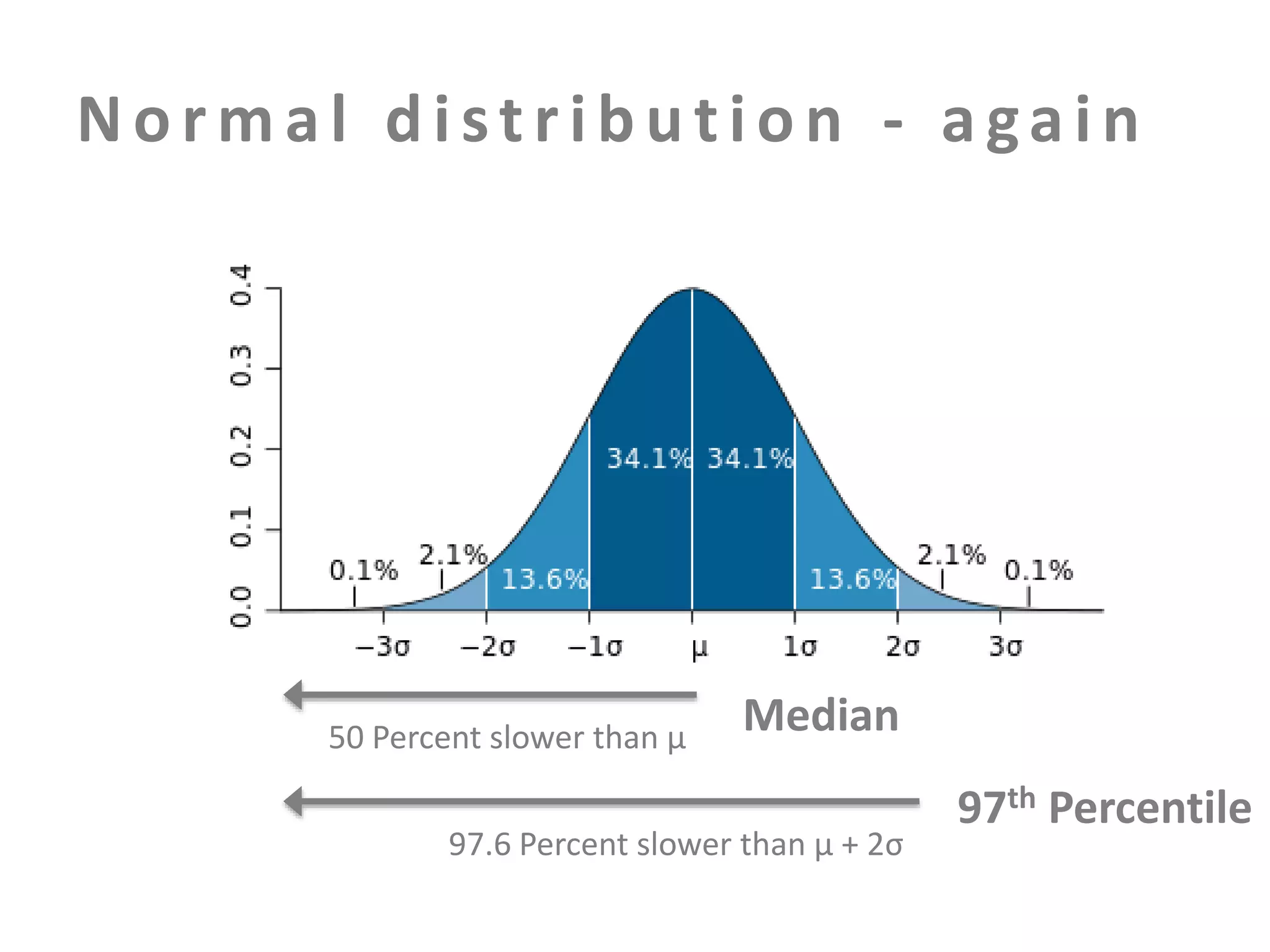
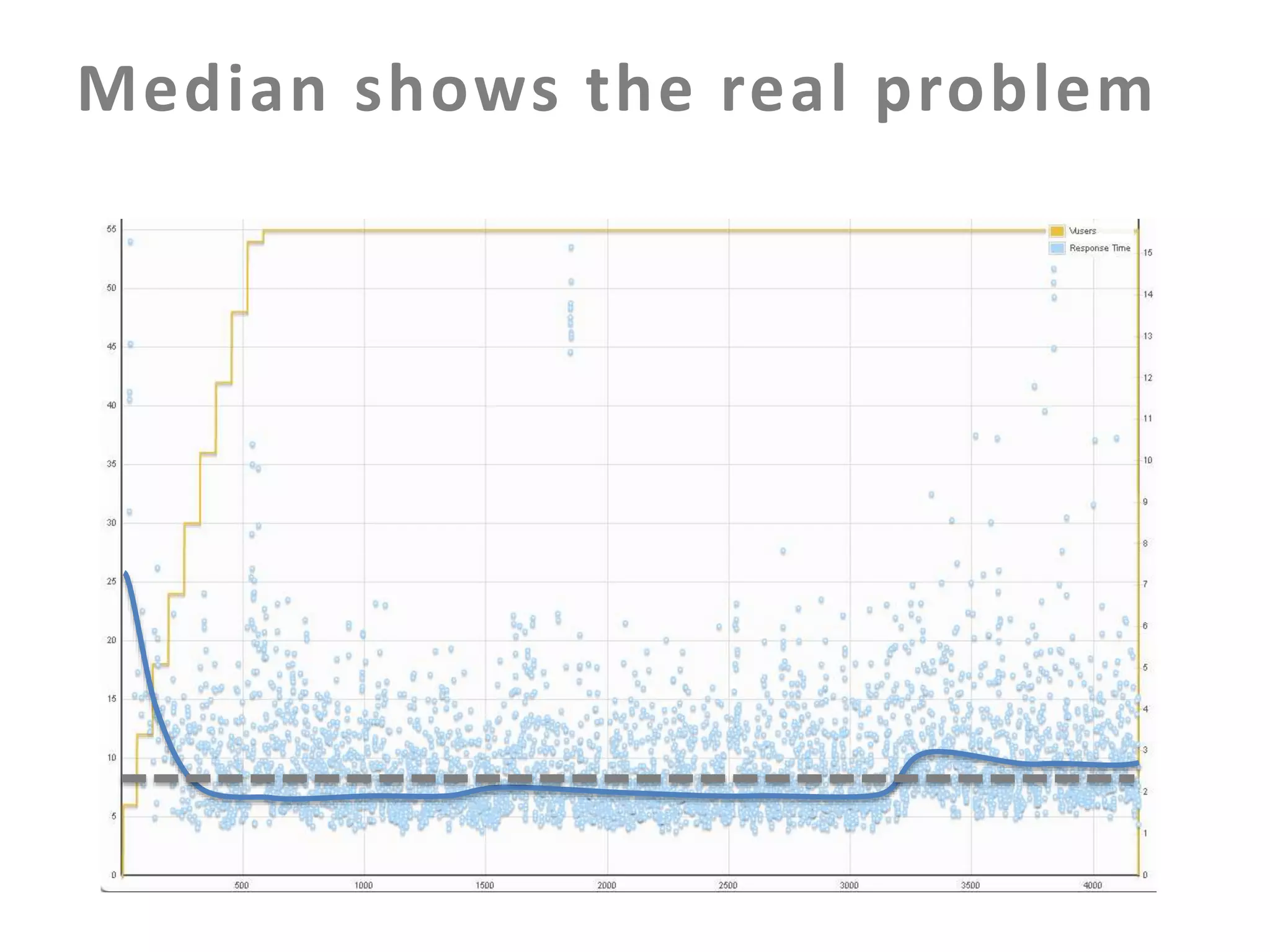
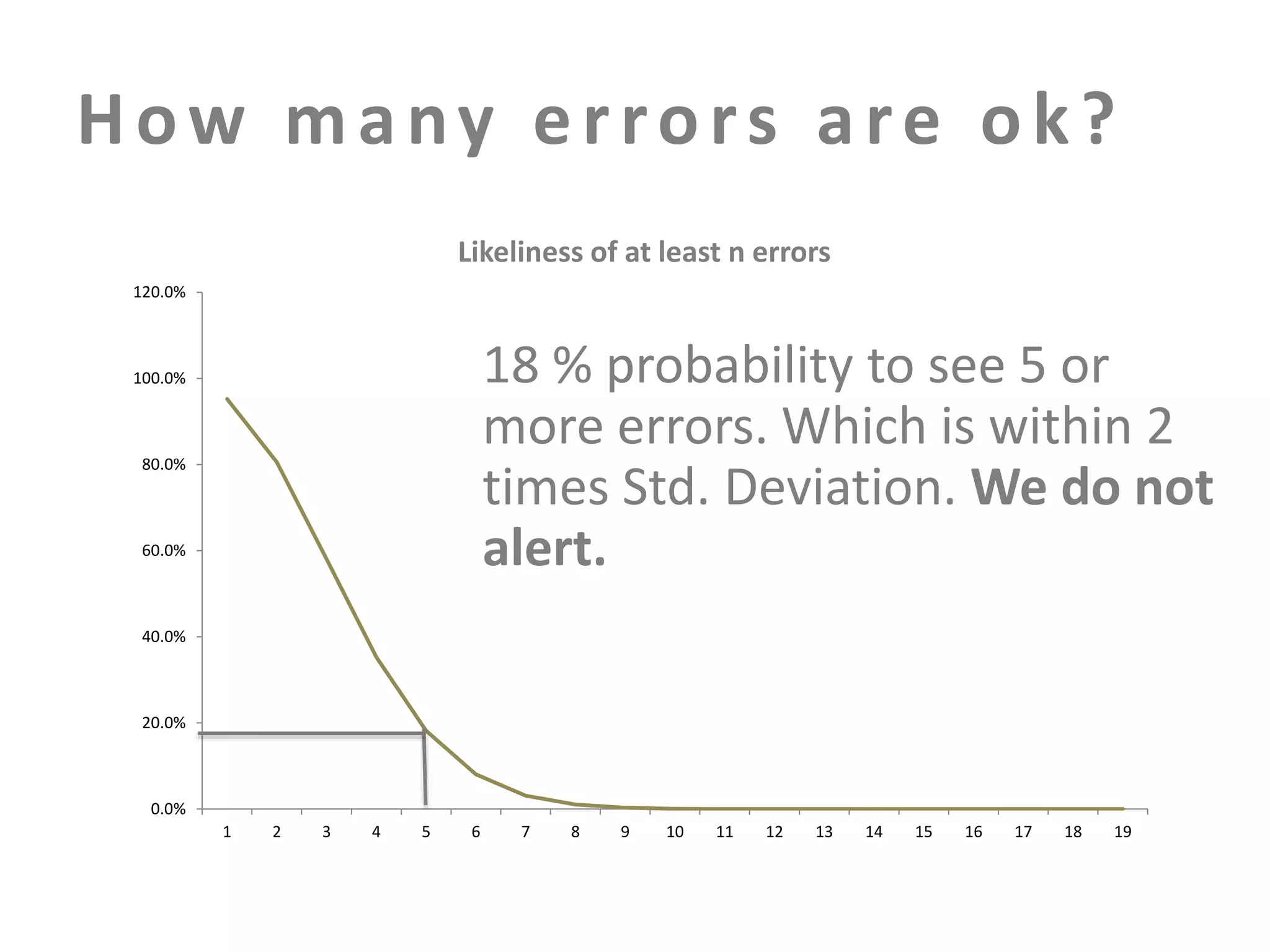
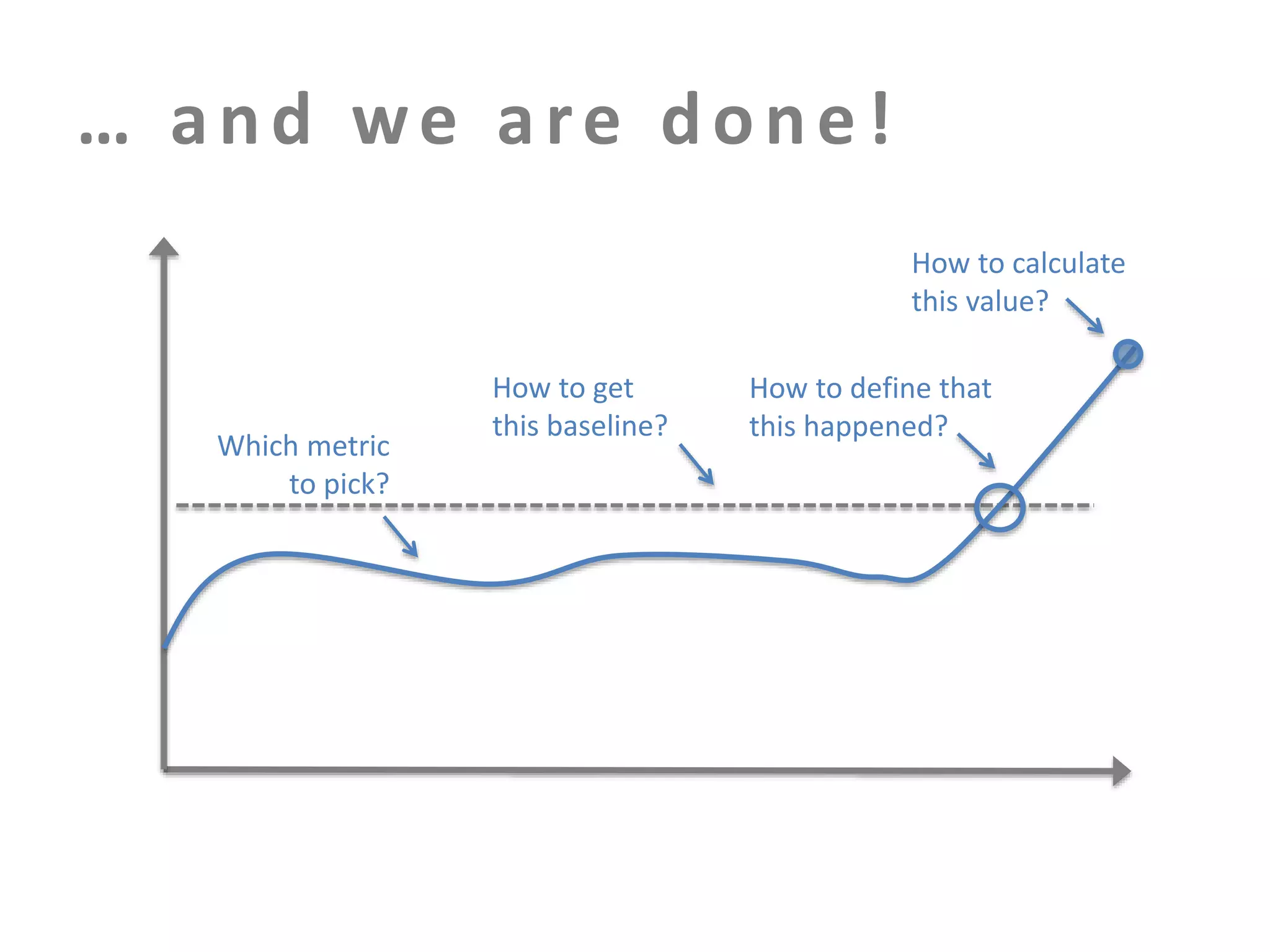
The document discusses building an effective production incident system using statistics. It explains that using the median and percentiles to define a baseline range captures normal system behavior better than trying to fit a specific distribution model. Two examples are provided: 1) Using the binomial distribution to determine if an error rate exceeds expectations. 2) Using percentiles to check if response times have drifted above the median without knowing the underlying distribution. The key is applying statistical methods to objectively determine what constitutes a normal range of values versus a problem requiring alerting.
More Related Content
Similar to The Dark of Building an Production Incident Syste
More from Alois Reitbauer
The Dark of Building an Production Incident Syste
- 1. The Dark Artof Building a Production Incident System @Alois Reitbauer Tech. Evangelist & Product Mgr., Compuware
- 2.
- 3.
- 4. Other things canhappen as well Continuous deployments Infrastructure changes other “everyday” stuff
- 5. Scaling an incidentsystem
- 6. How it feelsto do what we do
- 7. Do you alert? Typicalerror rate of 3 percent at 10.000 transactions/min During the night we now have 5 errors in 100 requests.
- 8. Do you alert? Typicalresponse time has been around 300 ms. Now we see response times up to 600 ms.
- 9. We a re g o o d a t f i x i n g problems, but not really good at detecting them.
- 10. How can weget better? .
- 11. It is allabout statistics I t ’s a l l a b o u t s t a t i s t i c s
- 12. Statistics is about objectivelylying to yourself in a meaningful way.
- 13. How to designan incident
- 14. It looks reallysimple How to calculate this value? Which metric to pick? How to get this baseline? How to define that this happened?
- 15. Which metrics topick?
- 16. Three types ofmetrics Capacity Metrics Define how much of resource is used. Discrete Metrics Simple countable things, like errors or users. Continuous Metrics Metrics represented by a range of values at any given time.
- 17. Capacity Metrics Good forcapacity planning, not so good for production alerting
- 18.
- 19. b e tter u s e Connection acquisition time Tells you, whether anyone needed a connection and did not get it.
- 20.
- 21. b e tter u s e Combination of Load Average and CPU usage even better correlate the with response times of applications
- 22. D i sc re te M e t r i c s Pretty easy to track and analyze.
- 23. C o nti n u o u s M e t r i c s Require some extra work as they are not that easy to track.
- 24. Continuous Metrics –The hope 42
- 25. Continuous Metrics –The reality
- 26. What the averagetells us
- 27. What the mediantells us
- 28. How to geta baseline?
- 29. A baseline isnot a number Baselines define the range of a value combined with a probability
- 30. Normal distribution asbaseline Mean: 500 ms Std. Dev.: 100 ms 0 100 200 300 400 500 600 68 % 400ms – 500 ms 95 % 300ms – 700 ms 99 % 200ms – 800 ms 700 800 900
- 31. This can goreally wrong “Why alerts suck and monitoring solutions need to become better”
- 32. How this leadsto false alerts
- 33. Many false alerts AggressiveBaseline
- 34. No alerts atall Moderate Baseline
- 35. Find the rightdistribution model However, this can be really hard to impossible
- 36. Your distribution mightlook like this
- 37. … or likethis
- 38. or completely different younever know …
- 39. How can wesolve this problem?
- 40. Normal distribution -again 50 Percent slower than μ Median 97.6 Percent slower than μ + 2σ 97th Percentile
- 41. The 50 thand 90 th percentile define normal behavior without needing to know anything about the distribution model
- 42. Median shows thereal problem
- 43. How to definenonnormal behavior?
- 44. Fortunately this isnot the problem we need to solve We are only talking about missed expectations
- 45. Let’s look attwo scenarios Errors Is a certain error rate likely to happen or not? Response Times Is a certain increase in response time significant enough to trigger an incident?
- 46. The error ratescenario We have a typical error rate of 3 percent at 10.000 transactions/minute During the night we now have 5 errors in 100 requests. Should we alert – or not?
- 47. What can welearn
- 48.
- 49. B i no m i a l D i st r i b u t i o n Tells us how likely it is to see n successes in a certain number of trials
- 50. How many errorsare ok? Likeliness of at least n errors 120.0% 18 % probability to see 5 or more errors. Which is within 2 times Std. Deviation. We do not alert. 100.0% 80.0% 60.0% 40.0% 20.0% 0.0% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
- 51. Response Time Example Ourmedian response time is 300 ms and we measure 200 ms 500 ms 400 ms 150 ms 350 ms 350 ms 200 ms 400 ms 600 ms 600 ms
- 52.
- 53. Did the mediandrift significantly? Check all values above 300 ms 200 ms 500 ms 400 ms 150 ms 350 ms 350 ms 200 ms 400 ms 600 ms 600 ms 7 values are higher than the median. Is this normal? We can again use the Binomial Distribution
- 54. Applying the Binomial Distribution Wehave a 50 percent likeliness to see values above the median. How likely is is that 7 out of 10 samples are higher? The probability is 17 percent, so we should not alert.
- 55. … and weare done! How to calculate this value? Which metric to pick? How to get this baseline? How to define that this happened?
- 56. This was justthe beginning There are many more use things about statistics, probabilities, testing, ….
- 57.
- 58.