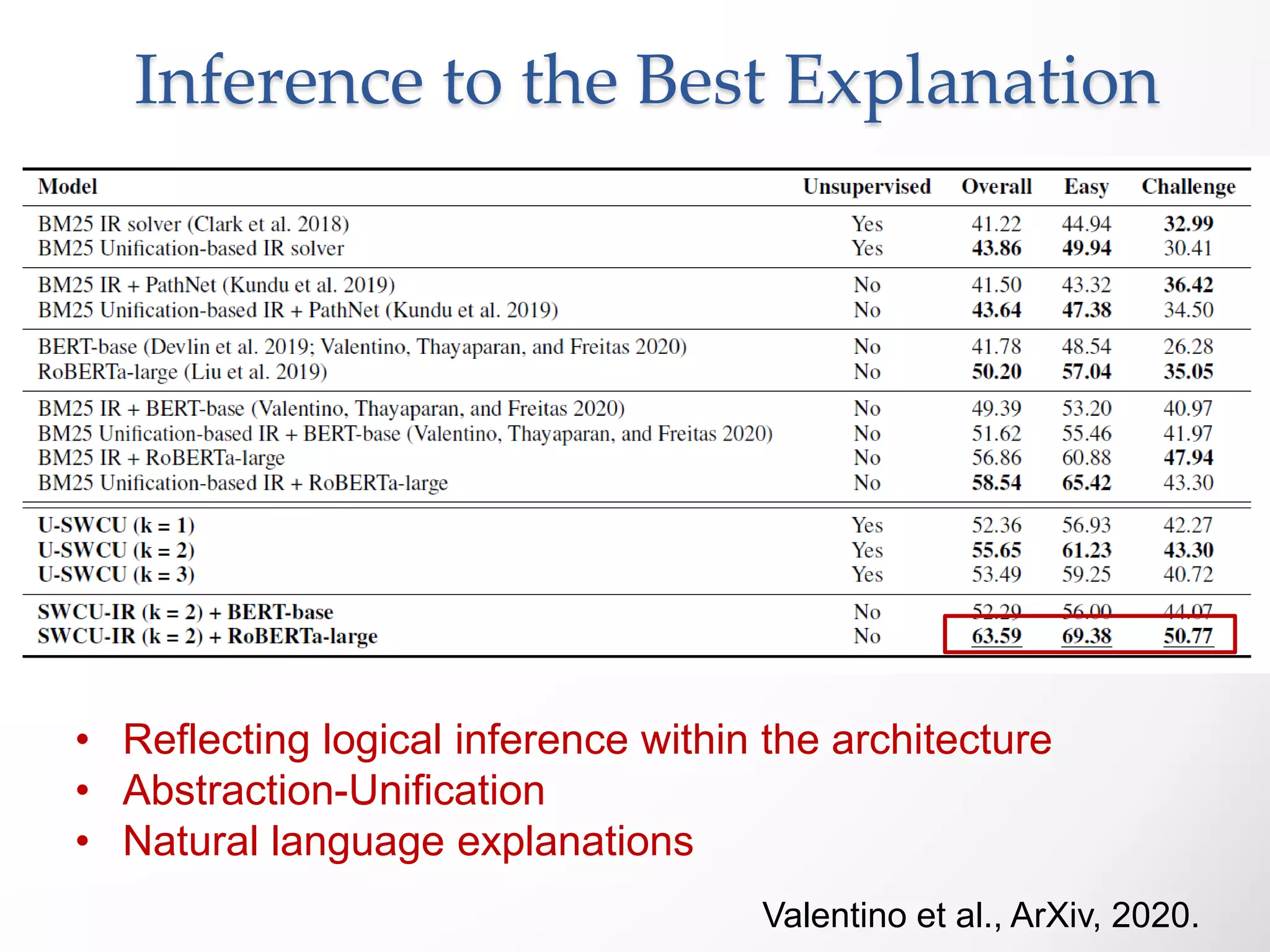
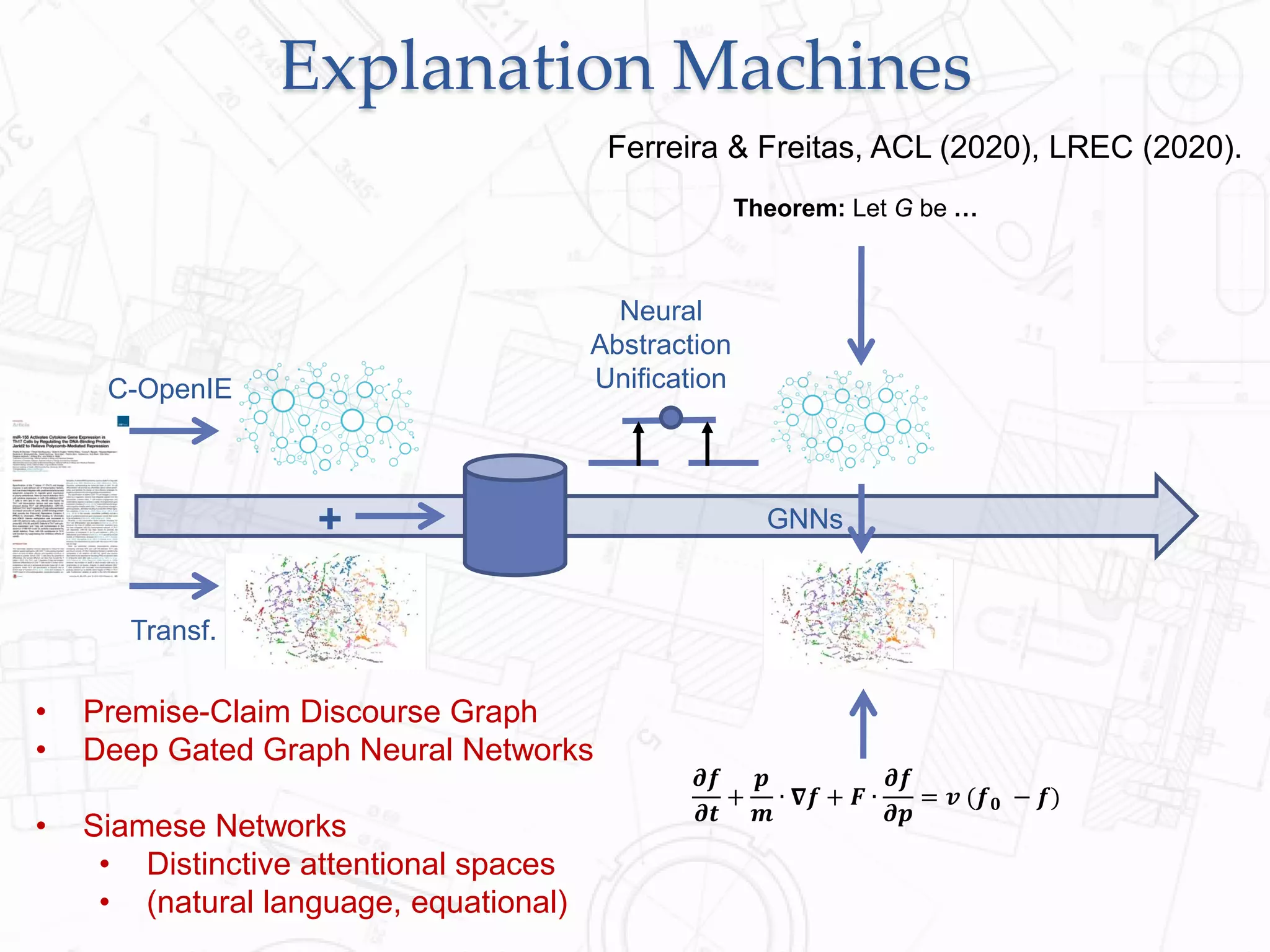
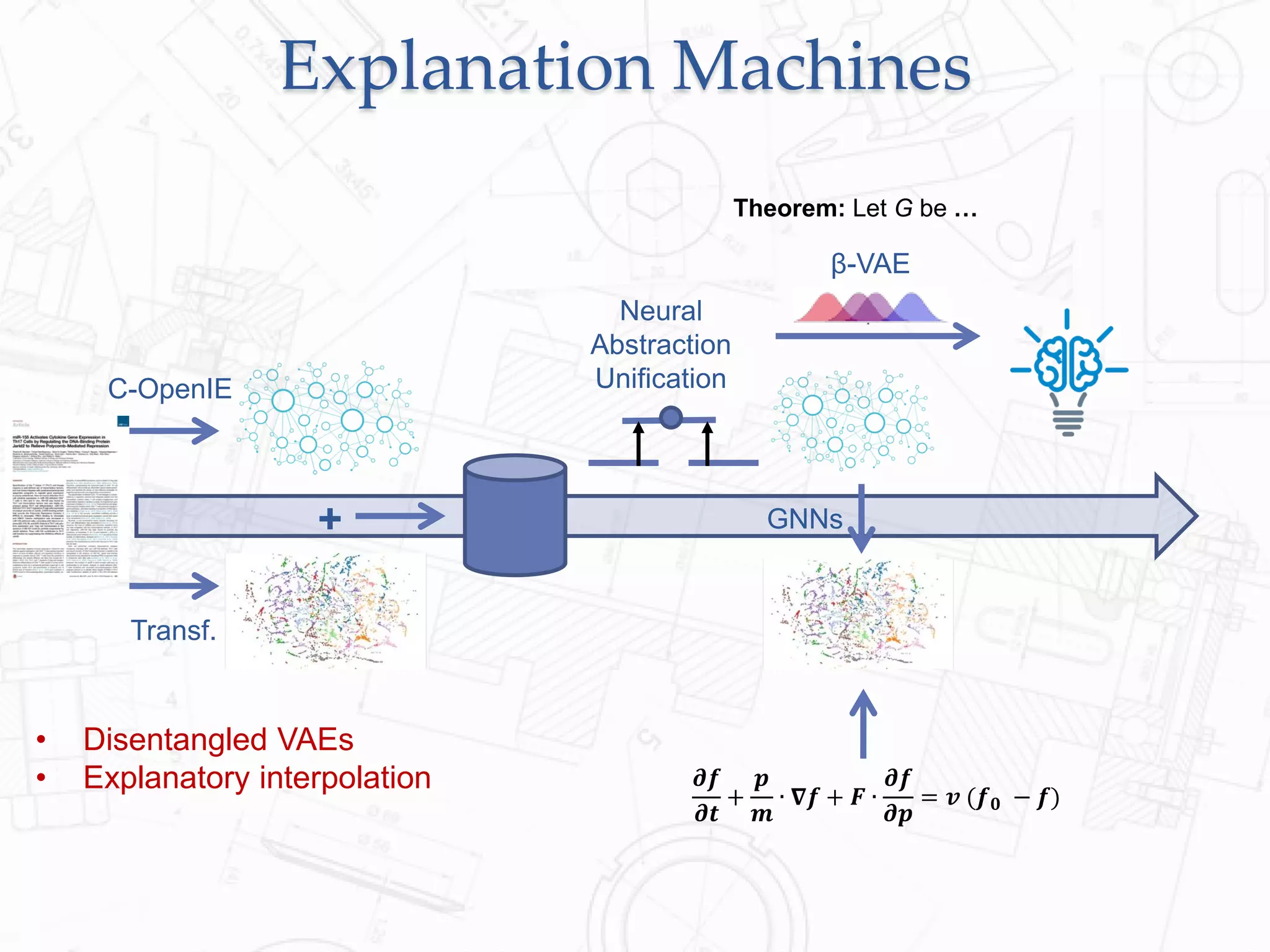
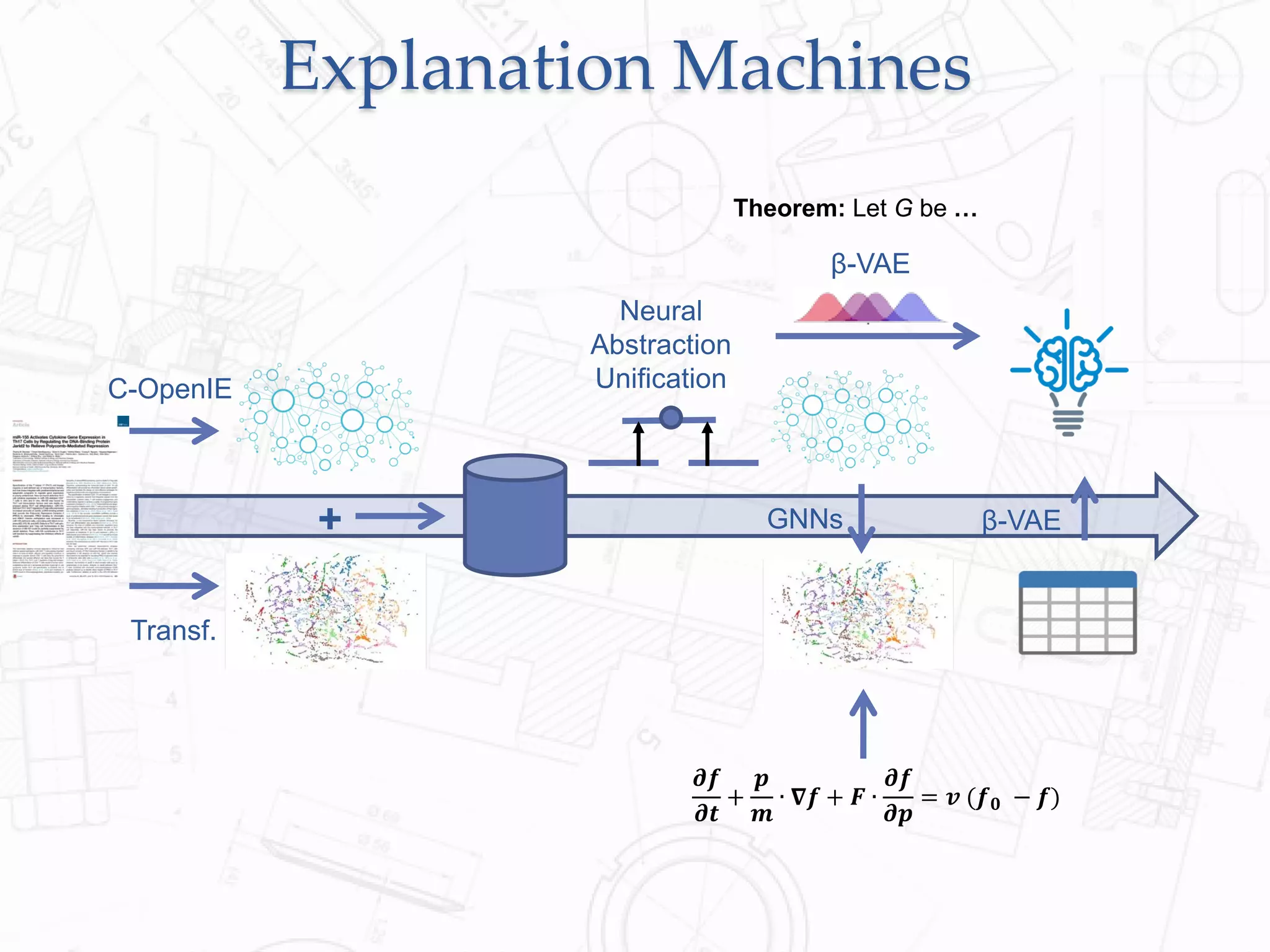
Here are the steps to prove the claim: 1) By Lagrange's theorem, the order of any subgroup H of G divides the order of G. 2) Since the order of G is pn, the only possible orders for subgroups are 1, p, p2, ..., pn. 3) Therefore any composition series for G will have abelian factor groups of prime power order, so G is solvable.

1. AI Systems Lab:
Explainable, Knowledge-based &
Trustworthy AI

3. AI Systems Lab
• Neuro-Symbolic
• Deep Inference
• Explainable
• Transparent
• Safe
• AI Architectures
• AI Systems
• Augmented Science
• AI4Science
• AI4CancerResearch
Artificial Intelligence
Natural Language Processing
Data Management

4. AI Systems Lab

5. Vision – Elevator Pitch
• The Problem: Deep learning-based AI:
o Black box, untrustworthy
o Shallow explanations
• The aim: Building an AI paradigm which is capable of
flexible, abstractive, complex and explainable
inference.
• How: Neuro-symbolic architectures which are data
scalable.
• Implications: Scaling-up knowledge production & scientific
discovery.
Industrial scale inference.

6. Building ‘Explanation Machines’

7. Industrial scale inference

8. AI Systems Lab
• Building ‘Explanation Machines’
• Deep Inference
o Explainable & Knowledge-based AI
o Neuro-symbolic
• Natural Language Processing
• Data Management
Applications:
Cancer Research, Advanced Materials, Finance, Law

9. The Augmented Expert
https://human-centered.ai/project/explainable-ai-fwf-32554/
Social
Knowledge
Hypotheses
Questions
Explainable &
Knowledge-based AI

10. The Augmented Expert
• Molecular tumour boards
• Experimental medicine: cancer clinical trials
• Personalised & Data-driven

11. Patient with prostate cancer, R130STOP mutation in PTEN gene
AI Model recommends clinical trial NCT02975934
because:
o R130STOP causes loss of PTEN function - COSMIC database
o PTEN protein is involved in homologous recombination repair - KEGG pathway
o Loss of PTEN function causes a defect in homologous recombination repair - source
o A defect in homologous recombination repair makes cells sensitive to DNA double strand breaks - source
o Inhibition of the DNA base excision repair pathway blocks DNA single strand break repair - KEGG pathway
o Blockage of DNA single strand break repair leads to creation of DNA double strand breaks - source
o PARP1 is part of the DNA single strand break repair pathway - KEGG pathway
o -> PARP1 inhibition might be effective in this patient.
o No PARP inhibitors are approved in the UK for treatment of prostate cancer.
o Rucaparib inhibits PARP1 - NCI thesaurus
o Rucaparib is approved in the UK for treatment of ovarian, fallopian tube and peritoneal cancers - NICE
§ (Rucaparib is well-tolerated)
o NCT02975934 includes rucaparib - AACT
o NCT02975934 is currently recruiting - AACT
o NCT02975934 has open sites in the UK - AACT
o NCT02975934 is enrolling patients with prostate cancer - AACT
Explainable & Knowledge-based AI

12. “miR-155 activates cytokine gene expression
in Th17 Cells by Regulating the DNA-Binding
Protein Jarid2 to relieve Polycomb-mediated
repression.”

13. Patients with SARS-
Cov-2 confirmed by
PCR
Patients without SARS-
Cov-2 confirmed by
PCR
Median age (IQR)—years 63 (53–72) 60 (49–73)
Male 787/1,309 (60.1%) 90/167 (53.9%)
Race/ethnicity—Hispanic 577/1,268 (45.5%) 62/167 (37.1%)
Race/ethnicity—African
American
278/1,268 (21.9%) 46/167 (27.5%)
Race/ethnicity—White 277/1,268 (21.8%) 43/167 (25.7%)
Race/ethnicity—Asian 73/1,268 (5.8%) 5/167 (3.0%)
Race/ethnicity—Other 63/1,268 (5.0%) 11/167 (6.6%)
Obesity (BMI ≥30) 465/1,176 (39.5%) 34/149 (22.8%)a
Comorbidities—
hypertension
420/1,268 (33.1%) 67/167 (40.1%)
Comorbidities—diabetes 293/1,268 (23.1%) 34/167 (20.4%)
Comorbidities—CKD 167/1,268 (13.2%) 27/167 (16.2%)
… … …
Del Valle et al. , Nature Medicine (2020)

14. 𝝏𝒇
𝝏𝒕
+
𝒑
𝒎
∙ 𝛁𝒇 + 𝑭 ∙
𝝏𝒇
𝝏𝒑
= 𝒗 (𝒇 𝟎 − 𝒇)
Language!

15. Building Explanation Machines
Representation
Inference &
Explanation
Explanation and language at the centre
From Deep Learning to Deep Inference
ApplicationsTransparency

16. Representation

17. “A fluoroscopic study known as an upper gastrointestinal
series is typically the next step in management, although if
volvulus is suspected, caution with non water soluble
contrast is mandatory as the usage of barium can impede
surgical revision and lead to increased post operative
complications.”
Complex Sentence Representation
Knowledge Graph
Cetto et al., COLING (2018), Niklaus et al. ACL (2019).

18. A fluoroscopic study
is typically the next
step in management.
This fluoroscopic study
is known as an upper
gastrointestinal series.
Caution with non water
soluble contrast is
mandatory.
The usage of barium can
impede surgical revision.
Vovulus is suspected
The usage of barium can
lead to increased post
operative complications.
ELABORATION
core
LIST
BACKGROUND
CONTRAST
CONDITION
context
context
context
core
context
core core
core
core
Minimal, self-contained
propositions
Semantically interconnected
Hierarchically ordered
Clausal-Phrasal Disembedding (CPD)
Cetto et al., COLING (2018), Niklaus et al. ACL (2019).
Complex Sentence Representation

19. Context-preserving
Robust
State-of-the-art open
information extraction
Cetto et al., COLING (2018), Niklaus et al. ACL (2019).
https://github.com/Lambda-3/Graphene
Complex Sentence Representation

20. Explanation Machines
C-OpenIE

21. Explanation Machines
C-OpenIE
Transf.
Cetto et al., COLING (2018), Niklaus et al. ACL (2019).
• C-OpenIE: Shows better grammaticality, minimality, context
preservation and overall accuracy.
• Robust extraction in complex discourse.

22. =
Graph
• Symbolic
• Delivers Explanations
• Multi-hop Inference
Vector
• Statistical
• Delivers Approximation
• Robust to noise

23. Explanation Machines
C-OpenIE
Transf.
+
Freitas et al., IUI (2014), DKE (2015).
Thayaparan et al., TextGraphs@EMNLP (2019).
• Joint Embeddings + Knowledge Graphs query plans
• Index structures
• Scalability

24. Scalable Evidence Retrieval
“Is there any association between Jarid2
and miR-155 in Th17 cells?"
BIOASQ Challenge
"Jarid2 links MicroRNA and chromatin in Th17 cells."
"miR-155 activates cytokine gene expression in Th17 cells by
regulating the DNA-binding protein Jarid2 to relieve polycomb-
mediated repression."
"Mir155 was bound by Th17 cell transcription factors and
was highly expressed during Th17 cell differentiation.
miR-155-deficient Th17 and T regulatory (Treg) cells
expressed increased amounts of Jarid2, a DNA-binding
protein that recruits the Polycomb Repressive Complex 2
(PRC2) to chromatin. PRC2 binding to chromatin and
H3K27 histone methylation was increased in miR-155-
deficient cells, …."
"Defects in Th17 cell cytokine expression and Treg cell homeostasis in
the absence of Mir155 could be partially suppressed by Jarid2
deletion. Thus, miR-155 contributes to Th17 cell function by
suppressing the inhibitory effects of Jarid2."
Evidence
Retrieval
Answer: Yes.

25. Scalable Evidence Retrieval
https://github.com/Lambda-3/Stargraph
“AI Database”
Freitas et al., IUI (2014), DKE (2015).
Thayaparan et al., TextGraphs@EMNLP (2019).

26. Scalable Evidence Retrieval
“Is there any association between Jarid2
and miR-155 in Th17 cells?"
"Activation-induced miR-155 targets the chromatin
protein Jarid2 to regulate proinflammatory cytokine
production in T helper 17 cells."
BIOASQ Challenge
"Jarid2 links MicroRNA and chromatin in Th17 cells."
"miR-155 activates cytokine gene expression in Th17 cells by
regulating the DNA-binding protein Jarid2 to relieve polycomb-
mediated repression."
"Mir155 was bound by Th17 cell transcription factors and
was highly expressed during Th17 cell differentiation.
miR-155-deficient Th17 and T regulatory (Treg) cells
expressed increased amounts of Jarid2, a DNA-binding
protein that recruits the Polycomb Repressive Complex 2
(PRC2) to chromatin. PRC2 binding to chromatin and
H3K27 histone methylation was increased in miR-155-
deficient cells, …."
"Defects in Th17 cell cytokine expression and Treg cell homeostasis in
the absence of Mir155 could be partially suppressed by Jarid2
deletion. Thus, miR-155 contributes to Th17 cell function by
suppressing the inhibitory effects of Jarid2."
Evidence
Retrieval
Explanation
Answer: Yes.

27. Explanation &
Inference

28. Representing Inference Chains
(From Deep Learning to Deep Semantics)
H: Shale is a sedimentary rock that can be
metamorphosed into slate by increased pressure.
'high is similar to increase'
'exposure to extreme heat and pressure changes
metamorphoses sedimentary and igneous rock into
metamorphic rock'
'shale is a kind of sedimentary rock'
'extreme means very high in value'
Valentino et al. Unification-based Reconstruction of Explanations for
Science Questions, 2020.

29. Representing Inference Chains
(From Deep Learning to Deep Inference)
Patient with prostate cancer, R130STOP mutation in PTEN gene
because:
o R130STOP causes loss of PTEN function
o PTEN protein is involved in homologous recombination repair
o Loss of PTEN function causes a defect in homologous recombination repair
o A defect in homologous recombination repair makes cells sensitive to DNA double strand breaks
o Inhibition of the DNA base excision repair pathway blocks DNA single strand break repair
o Blockage of DNA single strand break repair leads to creation of DNA double strand breaks
o PARP1 is part of the DNA single strand break repair pathway
o -> PARP1 inhibition might be effective in this patient.

30. Representing Inference Chains
(From Deep Learning to Deep Inference)
• Identify relevant facts
• Integrate separate pieces of evidence
• Abstract, unify
• Infer new knowledge
Neural and Formal

31. Valentino et al., ArXiv, 2020.
Abstraction
Unification
Inference to the Best Explanation

32. Inference to the Best Explanation
• Reflecting logical inference within the architecture
• Abstraction-Unification
• Natural language explanations
Valentino et al., ArXiv, 2020.

33. Explanation Machines
C-OpenIE
Transf.
+
Neural
Abstraction
Unification
Santos et al, AAAI (2018, 2019).
Valentino et al. ArXiv (2020).
• Reflecting logical inference within the architecture
• Abstraction-Unification
• Natural language explanations

34. Mathematical Discourse
Premise Selection
Claim: Let G be a group whose order pn where p is a prime
number and n is a positive integer. Then G is solvable.
Theorem: Let G be a group such that
|G|= pn where p is a prime number. Then
G has a composition series in which
each factor group is cyclic of order p.
Definition: Let G be a finite group. Then
G is a solvable group if and only if it has a
composition series in which each factor is
a cyclic group.

35. Mathematical Discourse
Ferreira & Freitas, ACL (2020), LREC (2020).

36. Explanation Machines
C-OpenIE
Transf.
+
Neural
Abstraction
Unification
GNNs
Theorem: Let G be …
𝝏𝒇
𝝏𝒕
+
𝒑
𝒎
∙ 𝛁𝒇 + 𝑭 ∙
𝝏𝒇
𝝏𝒑
= 𝒗 (𝒇 𝟎 − 𝒇)
• Premise-Claim Discourse Graph
• Deep Gated Graph Neural Networks
• Siamese Networks
• Distinctive attentional spaces
• (natural language, equational)
Ferreira & Freitas, ACL (2020), LREC (2020).

37. Explanation Machines
C-OpenIE
Transf.
+
Neural
Abstraction
Unification
GNNs
Theorem: Let G be …
𝝏𝒇
𝝏𝒕
+
𝒑
𝒎
∙ 𝛁𝒇 + 𝑭 ∙
𝝏𝒇
𝝏𝒑
= 𝒗 (𝒇 𝟎 − 𝒇)
β-VAE
• Disentangled VAEs
• Explanatory interpolation

38. Getting Creative
Generating Novel Explanations
Mercatali et al., 2020.

39. Explanation Machines
C-OpenIE
Transf.
+
Neural
Abstraction
Unification
GNNs
Theorem: Let G be …
𝝏𝒇
𝝏𝒕
+
𝒑
𝒎
∙ 𝛁𝒇 + 𝑭 ∙
𝝏𝒇
𝝏𝒑
= 𝒗 (𝒇 𝟎 − 𝒇)
β-VAE
β-VAE

40. Explanation Machines:
From Deep Learning to Deep Semantics
Scalable Approximate
Unification
Freitas et al. DKE (2015)
Explainable Entailment
Santos et al. AAAI (2018)
Explainable Entailment
Santos et al. AAAI (2019)
Multi-hop Inference
using GNs
Thayaparan et al.,
TextGraphs@EMNLP (2019)
Discriminative Attributes
Stepanjans & Freitas,
EMNLP (2019)
Premise Selection
Ferreira & Freitas,
ACL (2020)
Unification
Reconstruction
Valentino et al.,
ArXiv (2020)
Explanatory Novelty
Mercatalli et al. (2020)
Sentence Spliting
Niklaus et al., ACL (2019)
Graph Extraction
Cetto et al., COLING (2019)

41. Symb. Inference
Explicit
Representation
Neural Learning
Numerical/Latent
Knowledge Extraction,
Retention, Consolidation
Knowledge Transfer,
Inductive Bias
Hypotheses, Answers, Explanations
Virtuous
Cycle
Inf. Extraction
Complex Text
Representation
Expert Knowledge
Generalisation,
Robust to Noise
Deep inference
Explainability
Data efficiency
Adapted from Silver (2013)
Knowledge-based & Explainable AI

42. Transparency
https://medium.com/tech-accounts/democratized-ai-the-black-box-problem-d70145e4a606

43. G.Marshall, C. Jay, A. Freitas, Diagrammatic Signification of Artificial Intelligence Systems: Insight from a
heterogeneous landscape (2020).
G.Marshall, A. Freitas, C. Jay, How Researchers Use Diagrams in Communicating Neural Network Systems?
(2020).
G. Marshall, A. Freitas, Measuring diagram quality through semiotic morphisms, Semiotica (2019).
Xu et al (2018)
Song et al (2018)
Ye et al (2018)
Transparency & Representation

44. Applications

45. Personalised Clinical Trials
• Genome
• Transcriptome
• Proteome
• Metabolome
• …
• Cytokine Release Syndrome
• Predicting Toxicity Effects
• SARS-CoV-2/Oncology
e.g. Acute Kidney Injury
OCT scans

46. black areas surrounded on all sides by
retina , and shape is circular or oblong
black areas between retina and RPE ,
elongated and not circular , more
saucer shaped
If fluid is lots of areas that
are oblong with height >>
width and they are
arranged v close together
If cysts are very square
shaped and not with overall
retinal thickening and over
areas of atrophy
exudative cysts
Any areas of
discrete black,
darker than
expected and
not part of
normal retinal
layers
Subretinal fluid
Intraretinal fluid schisis cysts
Atrophic cysts
Retinal
fluid
No
Retinal
fluid
OR
yes
NO
NO
yes
yes
yes

47. Advanced Materials
Artificial Graphene models
Artificial Graphene - Emergence of Type-II Dirac Points

48. 𝐺 = (𝑁, Σ, 𝑃, 𝑆)
𝑙 𝑛𝑖
ℎ 𝑛 𝑗
ℎ 𝑛 𝑗
𝑙 𝑛𝑖
𝑙 𝑛𝑖
𝑙 𝑛𝑖
𝑙 𝑎 𝑖
ℎ 𝑎 𝑗
ℎ 𝑎 𝑗
𝑙 𝑎 𝑖
𝑥 𝑎 𝑘
𝑙 𝑎 𝑖
𝜏 𝑛
𝜏 𝑎
𝑝 𝑛 =
𝜐 𝑛
𝜏 𝑛
𝑝 𝑎 =
𝜐 𝑎
𝜏 𝑎
𝛿𝑝 =
𝑝 𝑎
𝑝 𝑛
Jacobo & Freitas 2020
Micro-economics & AI

49. Explanation construction for fact
checking
Industrial Collaborations
Text classification for the legal domain
Deep-learning based data integration
and discovery
Semantic Interpretation for Robotic
Process Automation

50. Explainable & Safe AI
https://enncore.github.io/
EnnCore: End-to-End Conceptual Guarding
of Neural Architectures
Explainability and Provability
(emphasis on clinical settings)

51. Take-away Message

53. Building Explanation Machines
• Industrial Scale inference
o Commoditisation of inference
• Linguistic + Logical + Neural
• Scalable architectures
• AI Models which can integrate noisy data and
abstract
• End-user driven: explainable and trustworthy

54. Building Explanation Machines
• AI defines a new epistemological foundation
• Industrial scale inference
• Architectural elements:
C-OpenIE
Transf.
+
Neural
Abstraction
Unification
GNNs
Theorem: Let G be …
𝝏𝒇
𝝏𝒕
+
𝒑
𝒎
∙ 𝛁𝒇 + 𝑭 ∙
𝝏𝒇
𝝏𝒑
= 𝒗 (𝒇 𝟎 − 𝒇)
β-VAE
β-VAE

55. With the generous support of

56. Collaborators