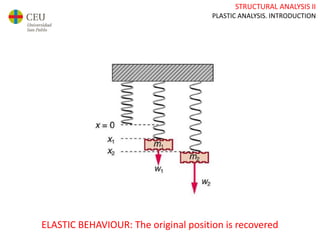
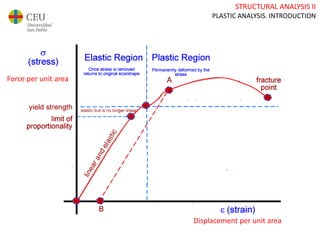
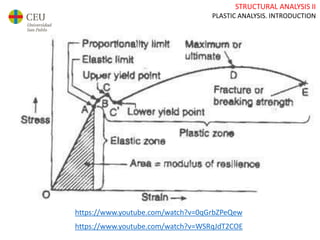
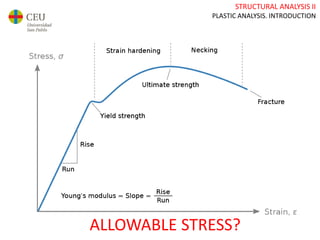
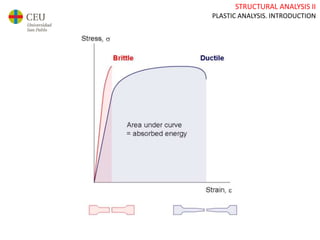
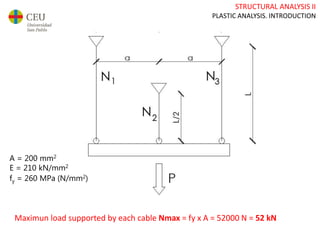
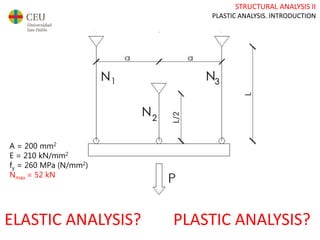
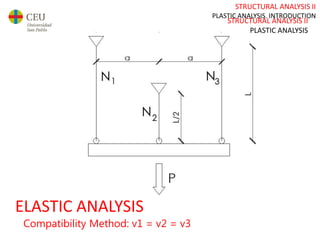
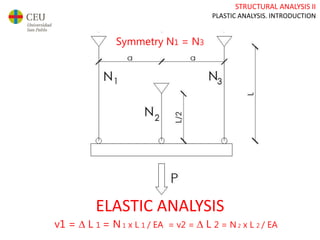
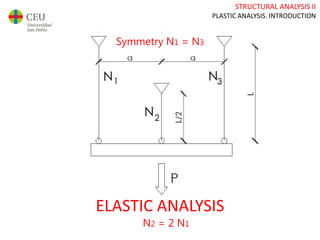
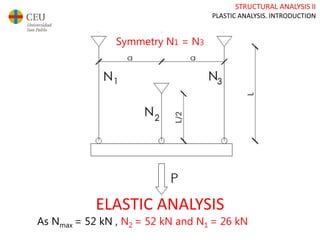
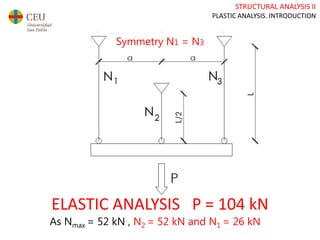
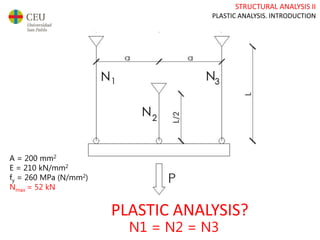
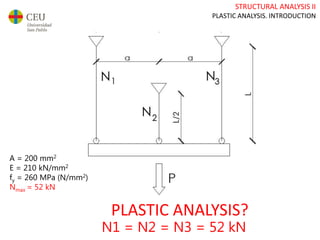
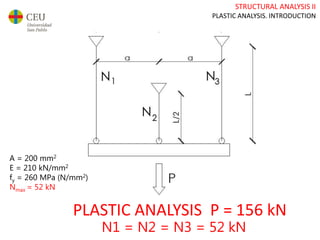
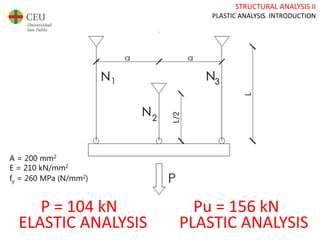
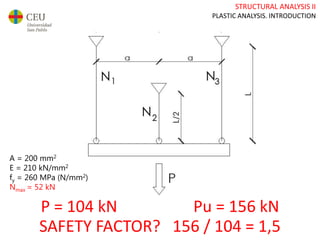
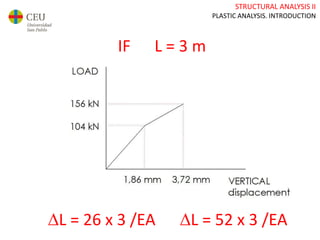
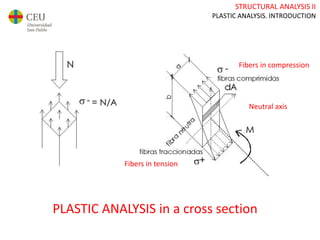
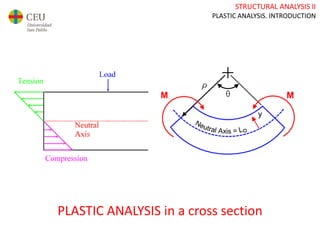
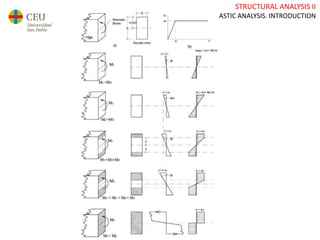
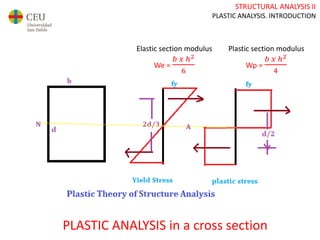
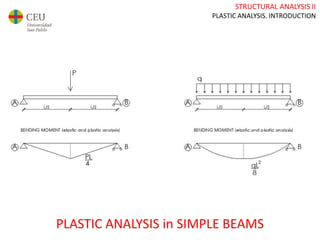
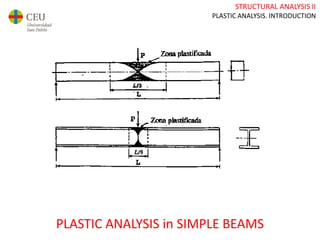
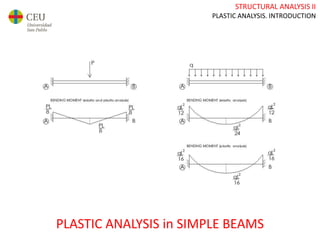
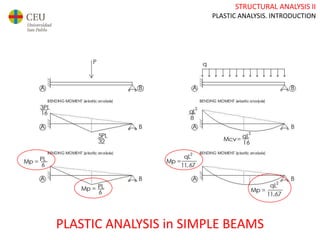
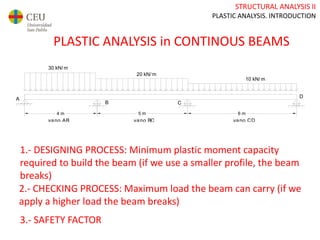
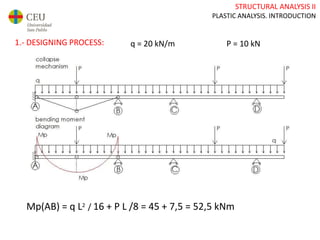
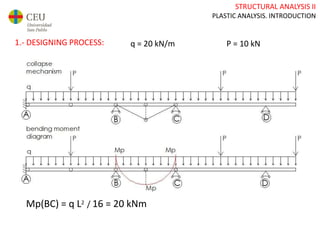
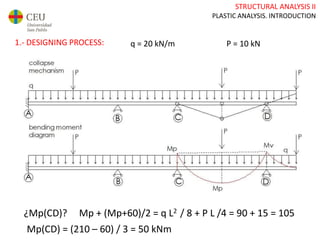
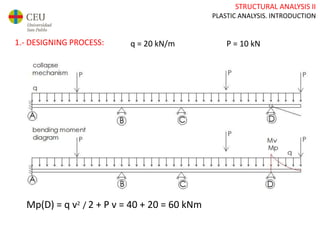
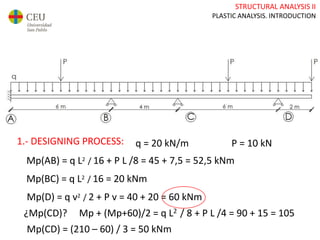
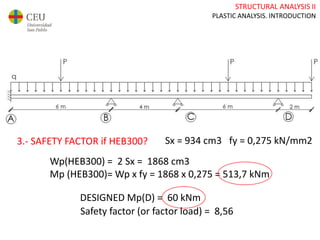
This document discusses plastic analysis of structures. It begins by introducing elastic and plastic behavior in materials. Plastic analysis is then compared to elastic analysis, noting that plastic analysis provides safer and more economical designs by allowing materials to yield while still supporting load. Methods for plastic analysis of beams, frames, and slabs are outlined. Key aspects of plastic analysis in cross-sections and simple/continuous beams are also summarized, including plastic hinge formation and required plastic moment capacities. Worked examples demonstrate how to determine minimum required plastic moments, maximum loads supported, and safety factors in plastic design.

1. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS

2. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
1.- ELASTIC ANALYSIS OF GRIDS
1.1.- COMPATIBILITY METHOD
1.2- SLOPE DEFLECTION METHOD
2.- PLASTIC ANALYSIS OF STRUCTURES
2.1- PLASTIC ANALYSIS OF BEAMS
2.2- PLASTIC ANALYSIS OF FRAMES
2.2.1- KINEMATIC METHOD
2.2.2- INCREMENTAL ANALYSIS. HINGE BY HINGE METHOD
3.- INTRODUCTION TO SECOND ORDER ANALYSIS OF STRUCTURES
2.3- PLASTIC ANALYSIS OF SLABS.
FEBRUARY
MARCH
APRIL

3. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS of beams
Specially useful to calculate one way slabs small continuous beams

4. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION

5. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ELASTIC BEHAVIOUR: The original position is recovered

6. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC BEHAVIOUR: The original position is NOT recovered

7. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
Force per unit area
Displacement per unit area

8. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
https://www.youtube.com/watch?v=0qGrbZPeQew
https://www.youtube.com/watch?v=WSRqJdT2COE

9. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ALLOWABLE STRESS?

10. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION

11. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ELASTIC ANALYSIS PLASTIC ANALYSIS
≠ RESULTS*
Part of the structure
material is working beyond
the plastic limit
The material should be
ductile enough to have a
plastic behaviour
All the structure material is
working below the plastic
limit
The material can be fragile
or ductile to apply elastic
analysis

12. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ELASTIC ANALYSIS PLASTIC ANALYSIS
≠ RESULTS*
Part of the structure
material is working beyond
the plastic limit
The structure should be
ductile enough to have a
plastic behaviour
All the structure material is
working below the plastic
limit
The structure can be
fragile or ductile to apply
elastic analysis
SAFER?
SAFER

13. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS
ELASTIC ANALYSIS PLASTIC ANALYSIS
≠ RESULTS*
Part of the structure
material is working beyond
the plastic limit
The material should be
ductile enough to have a
plastic behaviour
All the structure material is
working below the plastic
limit
The material can be fragile
or ductile to apply elastic
analysis
CHEAPER?
SAFER CHEAPER

14. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ELASTIC ANALYSIS PLASTIC ANALYSIS
≠ RESULTS*
Part of the structure
material is working beyond
the plastic limit
The material should be
ductile enough to have a
plastic behaviour
All the structure material is
working below the plastic
limit
The material can be fragile
or ductile to apply elastic
analysis
SAFER CHEAPER
Superposition Principle
cannot be applied
Superposition Principle can
be applied

15. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
A = 200 mm2
E = 210 kN/mm2
fy = 260 MPa (N/mm2)
Maximun load supported by each cable Nmax = fy x A = 52000 N = 52 kN

16. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ELASTIC ANALYSIS? PLASTIC ANALYSIS?
A = 200 mm2
E = 210 kN/mm2
fy = 260 MPa (N/mm2)
Nmax = 52 kN

17. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS
ELASTIC ANALYSIS
Compatibility Method: v1 = v2 = v3

18. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ELASTIC ANALYSIS
v1 = ∆ L 1 = N 1 x L 1 / EA = v2 = ∆ L 2 = N 2 x L 2 / EA
Symmetry N1 = N3

19. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ELASTIC ANALYSIS
N2 = 2 N1
Symmetry N1 = N3

20. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ELASTIC ANALYSIS
As Nmax = 52 kN , N2 = 52 kN and N1 = 26 kN
Symmetry N1 = N3

21. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ELASTIC ANALYSIS P = 104 kN
As Nmax = 52 kN , N2 = 52 kN and N1 = 26 kN
Symmetry N1 = N3

22. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS?
A = 200 mm2
E = 210 kN/mm2
fy = 260 MPa (N/mm2)
Nmax = 52 kN
N1 = N2 = N3

23. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS?
A = 200 mm2
E = 210 kN/mm2
fy = 260 MPa (N/mm2)
Nmax = 52 kN
N1 = N2 = N3 = 52 kN

24. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS P = 156 kN
A = 200 mm2
E = 210 kN/mm2
fy = 260 MPa (N/mm2)
Nmax = 52 kN
N1 = N2 = N3 = 52 kN

25. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
ELASTIC ANALYSIS PLASTIC ANALYSIS
A = 200 mm2
E = 210 kN/mm2
fy = 260 MPa (N/mm2)
P = 104 kN Pu = 156 kN

26. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
SAFETY FACTOR? 156 / 104 = 1,5
A = 200 mm2
E = 210 kN/mm2
fy = 260 MPa (N/mm2)
Nmax = 52 kN
P = 104 kN Pu = 156 kN

27. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
IF L = 3 m
DL = 26 x 3 /EA DL = 52 x 3 /EA

28. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
CONCLUSIONS?
Plastic analysis:
tells us that the same system can resist more load
Plastic analysis:
bigger displacements

29. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS in a cross section

30. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS in a cross section
Neutral axis
Fibers in compression
Fibers in tension

31. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS in a cross section

32. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION

33. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS in a cross section
Elastic section modulus
We =
𝑏 𝑥 ℎ2
6
Plastic section modulus
Wp =
𝑏 𝑥 ℎ2
4

34. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
SHAPE FACTOR
PLASTIC ANALYSIS in a cross section
Elastic section modulus / Plastic section modulus

35. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS in SIMPLE BEAMS

36. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS in SIMPLE BEAMS

37. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS in SIMPLE BEAMS

38. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS in SIMPLE BEAMS

39. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS in SIMPLE BEAMS

40. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
PLASTIC ANALYSIS in CONTINOUS BEAMS
30 kN/ m
4 m 5 m 6 m
20 kN/ m
10 kN/ m
vano AB vano BC vano CD
A
B C
D
HIPÓTESIS1 considerando la carga dada, calcular el momento plástico mínimo necesario para construir toda la viga
3
HIPÓTESIS2 considerando que la viga se construye con un IPE240 (Mp = 105,1 cm ) determina la carga de rotura.
HIPÓTESIS3 considerando la carga dada y el perfil IPE240 determina el factor de seguridad de la viga.
3
(mínimo momento de diseño)
1.- DESIGNING PROCESS: Minimum plastic moment capacity
required to build the beam (if we use a smaller profile, the beam
breaks)
2.- CHECKING PROCESS: Maximum load the beam can carry (if we
apply a higher load the beam breaks)
3.- SAFETY FACTOR

41. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
30 kN/ m
4 m 5 m 6 m
20 kN/ m
10 kN/ m
vano AB vano BC vano CD
A
B C
D
HIPÓTESIS1 considerando la carga dada, calcular el momento plástico mínimo necesario para construir toda la viga
3
HIPÓTESIS2 considerando que la viga se construye con un IPE240 (Mp = 105,1 cm ) determina la carga de rotura.
HIPÓTESIS3 considerando la carga dada y el perfil IPE240 determina el factor de seguridad de la viga.
3
(mínimo momento de diseño)
SPAN AB
SPAN BC
SPAN CD
Mp(AB) = q L2 / 11,67= 41,13 kNm
Mp(BC) = q L2 / 16= 20 x 25/16 = 31,25 kNm
Mp(CD) = q L2 / 11,67= 10 x 36/11,67 = 30,84 kNm
CAN WE TELL WHICH SPAN IS GOING TO FAIL FIRST?

42. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
2.- CHECKING PROCESS: Maximum load the beam can carry (if we
apply a higher load the beam breaks) (we know Wp, this is, the profile
capacity)
3.- SAFETY FACTOR (we know both the load and the profile
and the load value)
1.- DESIGNING PROCESS: Minimum plastic moment capacity
required to build the beam (if we use a smaller profile, the beam
breaks) (we know the load values)

43. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
1.- DESIGNING PROCESS: q = 20 kN/m P = 10 kN
Mp(AB) = q L2 / 16 + P L /8 = 45 + 7,5 = 52,5 kNm

44. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
1.- DESIGNING PROCESS: q = 20 kN/m P = 10 kN
Mp(BC) = q L2 / 16 = 20 kNm

45. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
1.- DESIGNING PROCESS: q = 20 kN/m P = 10 kN
¿Mp(CD)? Mp + (Mp+60)/2 = q L2 / 8 + P L /4 = 90 + 15 = 105
Mp(CD) = (210 – 60) / 3 = 50 kNm

46. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
1.- DESIGNING PROCESS: q = 20 kN/m P = 10 kN
Mp(D) = q v2 / 2 + P v = 40 + 20 = 60 kNm

47. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
1.- DESIGNING PROCESS: q = 20 kN/m P = 10 kN
Mp(AB) = q L2 / 16 + P L /8 = 45 + 7,5 = 52,5 kNm
Mp(BC) = q L2 / 16 = 20 kNm
Mp(D) = q v2 / 2 + P v = 40 + 20 = 60 kNm
¿Mp(CD)? Mp + (Mp+60)/2 = q L2 / 8 + P L /4 = 90 + 15 = 105
Mp(CD) = (210 – 60) / 3 = 50 kNm

48. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION
3.- SAFETY FACTOR if HEB300? Sx = 934 cm3 fy = 0,275 kN/mm2
DESIGNED Mp(D) = 60 kNm
Wp(HEB300) = 2 Sx = 1868 cm3
Mp (HEB300)= Wp x fy = 1868 x 0,275 = 513,7 kNm
Safety factor (or factor load) = 8,56

49. STRUCTURAL ANALYSIS II
PLASTIC ANALYSIS. INTRODUCTION