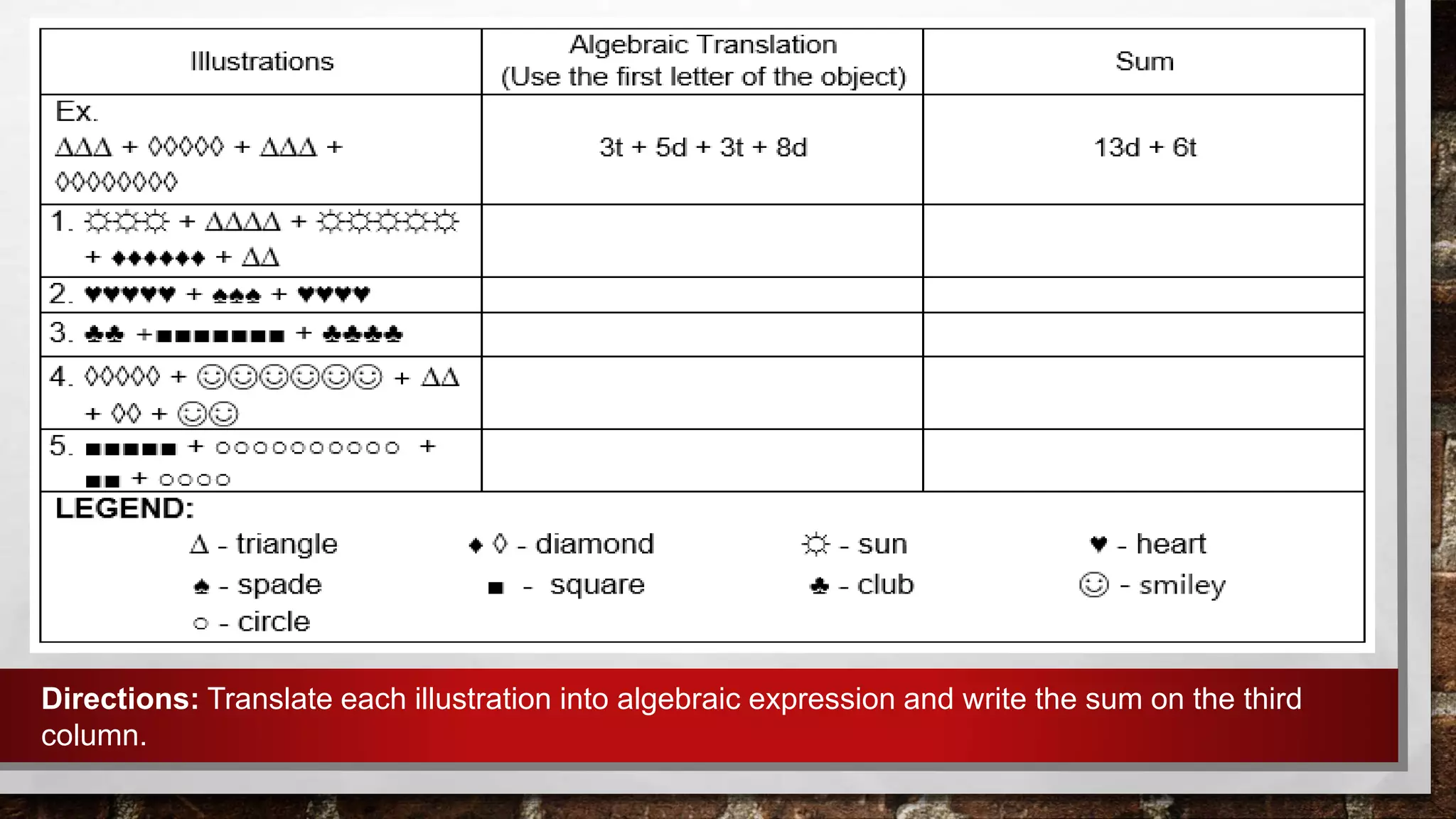
The document provides examples and steps for adding polynomials. It explains that to add polynomials, you combine like terms by getting the sum of the numerical coefficients and keeping the same literal coefficients. It shows how to add polynomials vertically by lining up like terms and horizontally by grouping like terms. Examples are provided for adding polynomials with one, two, and multiple terms. The key steps are to line up or group like terms and add the numerical coefficients in front of each term.