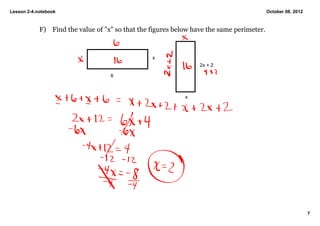
The document provides instructions and examples for a math lesson on solving equations. Students are assigned problems 3-39 on pages 100-101 due on Wednesday and asked to check if a test is signed. The lesson explains how to solve equations by moving variable terms to one side and combining like terms before simplifying. It provides examples of solving equations such as 2 + 5x = 3x - 6 and finding the value of x where two figures have the same perimeter.

1. Lesson 2­4.notebook October 08, 2012
Assignment:
1­­>L2.4, pg. 100­101, #3­39 [thirds] ­ Due Wednesday (10/10)
2­­>Test signed??
1

2. Lesson 2­4.notebook October 08, 2012
Lesson 2.4 WarmUp:
Solve each equation. Show all work for full credit.
1) 2b + 6 = 24
3
2) 22 ­ w = ­7
3
3) 0.6x + 9 = 14.4
4) Find 3 consecutive odd integers with the sum of 141.
5) Find 4 consecutive integers with a sum of ­142.
2

3. Lesson 2­4.notebook October 08, 2012
Lesson 2.4:
FYI...
*To solve an equation that has variables on each side of the equals sign, "move" the
variable terms so that they are all on one side.
*To "move" them ­ use the addition or subtraction property of equality
*When you move them to the new side...combine them with any other like terms.
*Also, remember to "simplify" before moving anything!
*.... 15 = 15 .... this is an "Identity" type of equation (all real #'s)
*.... 15 = 17 .... this is a "no solution" type of equation
3

4. Lesson 2­4.notebook October 08, 2012
Lesson 2.4 examples:
Solve each equation. Check your answer.
A) 2 + 5x = 3x ­ 6 check:
B) x/2 + 1 = 1/4x ­ 6 check:
4

5. Lesson 2­4.notebook October 08, 2012
C) 8x ­ 10 = 3(6 ­ 2x) check:
D) 7x + 5(x ­ 1) = ­5 + 12x check:
5

6. Lesson 2­4.notebook October 08, 2012
E) 6(y ­ 5) = 2(10 + 3y) check:
6

7. Lesson 2­4.notebook October 08, 2012
F) Find the value of "x" so that the figures below have the same perimeter.
x
2x + 2
6
x
7