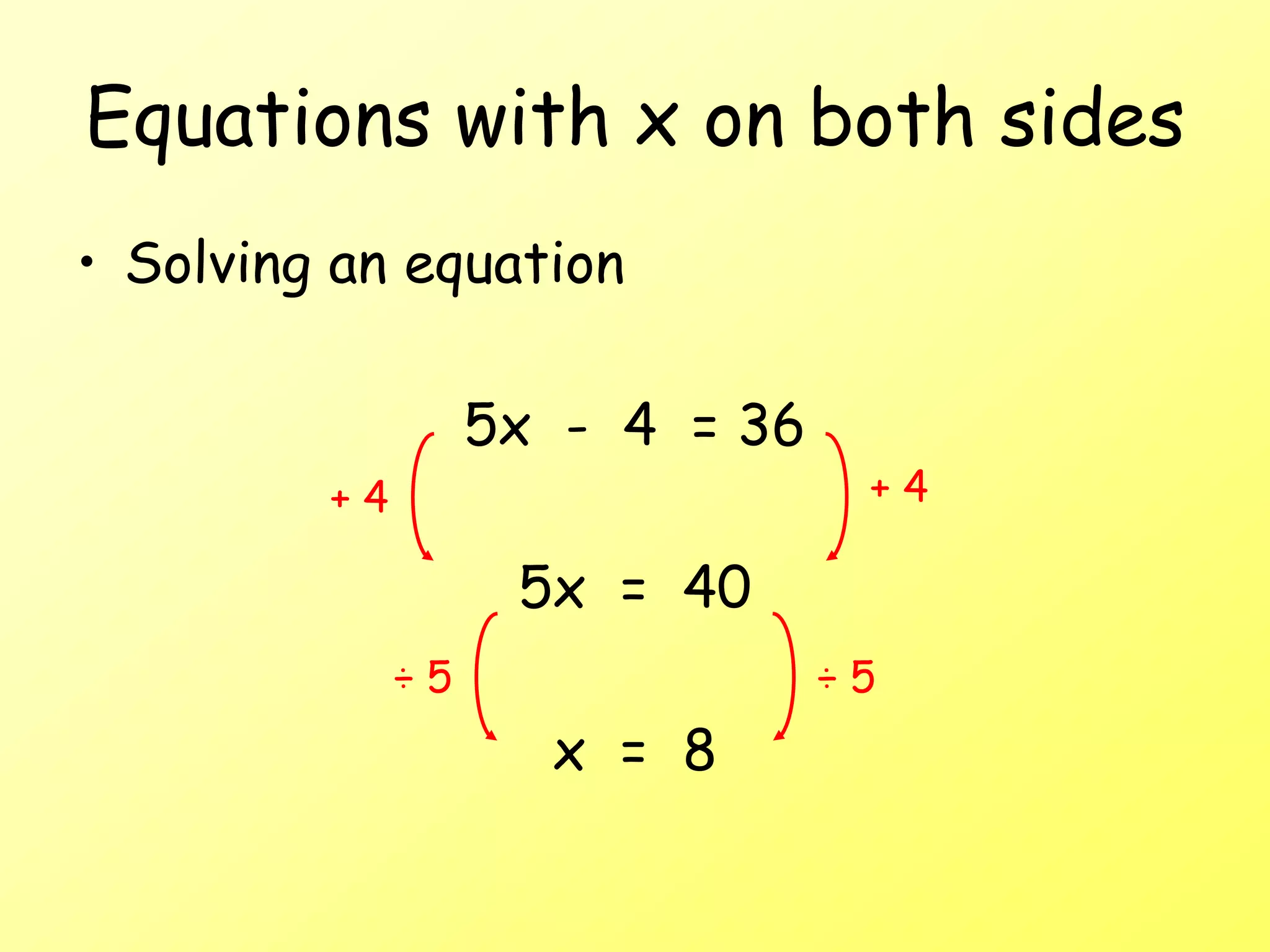The document discusses solving equations that have the variable x on both sides. It recaps the balancing method for solving equations and shows how this method can be extended to equations where x is on both sides. The additional step is to first rearrange the equation so that like terms involving x are together, and then apply the balancing method, being sure to move the smallest x value to one side of the equation. Examples are provided and discussed.

2. Starter
• Solve the following equation by the
‘balancing’ method…
4x + 8 = 32
4x = 24
x = 6
- 8 - 8
÷ 4
÷ 4

3. Equations with x on both sides
• Solving an equation
5x - 4 = 36
5x = 40
x = 8
+ 4 + 4
÷ 5
÷ 5

4. Equations with x on both sides
• Last lesson we looked at the ‘balancing’
method for solving an equation
• Today we will see how to use this
method to solve an equation with an
unknown (x) on both sides
• This will involve only one additional step
to before…

5. Equations with x on both sides
• Solving an equation
2x + 7 = 7x - 18
7 = 5x - 18
25 = 5x
5 = x
- 2x - 2x
+ 18
+ 18
÷ 5 ÷ 5
Rearrange
the ‘x’ parts
first!
Always move
the ‘smallest’
x value

6. Equations with x on both sides
• Solving an equation
3x - 4 = x + 6
2x - 4 = 6
2x = 10
x = 5
- x - x
+ 4
+ 4
÷ 2 ÷ 2
Rearrange
the ‘x’ parts
first!
Always move
the ‘smallest’
x value

7. Equations with x on both sides
• Solving an equation
4x - 7 = 7x - 19
- 7 = 3x - 19
12 = 3x
4 = x
- 4x - 4x
+ 19
+ 19
÷ 3 ÷ 3
Rearrange
the ‘x’ parts
first!
Always move
the ‘smallest’
x value

8. Equations with x on both sides
• Solving an equation
5 - x = 4x - 5
5 = 5x - 5
10 = 5x
2 = x
+ x + x
+ 5
+ 5
÷ 5 ÷ 5
Rearrange
the ‘x’ parts
first!
Always move
the ‘smallest’
x value

9. Equations with x on both sides
• Solving an equation
x - 1 = 17 - 2x
3x - 1 = 17
3x = 18
x = 6
+ 2x + 2x
+ 1
+ 1
÷ 6 ÷ 6
Rearrange
the ‘x’ parts
first!
Always move
the ‘smallest’
x value

10. Solving Equations – X on both sides
3(x + 3) = 5x - 5
3x + 9 = 5x - 5
Expand
the
bracket
9 = 2x - 5
- 3x
- 3x
14 = 2x
+ 5
+ 5
7 = x
÷ 2
÷ 2
Multiply out
the bracket
first!

11. Solving Equations – X on both sides
(2x + 3)/4 = 2x - 1
2x + 3 = 4(2x – 1)
Multiply
by 4
= 8x - 4
Expand
the
bracket
3 = 6x - 4
- 2x
- 2x
7 = 6x
+ 4
+ 4
2x + 3
÷ 6
÷ 6
1 1/6 = x
Multiply
by 4
Cancel out
the fraction
first!

12. Summary
• We have recapped solving equations
• We have extended this knowledge to
include equations with x on both sides
• Again, we have seen that the easiest
way to do this is by the ‘balancing’
method