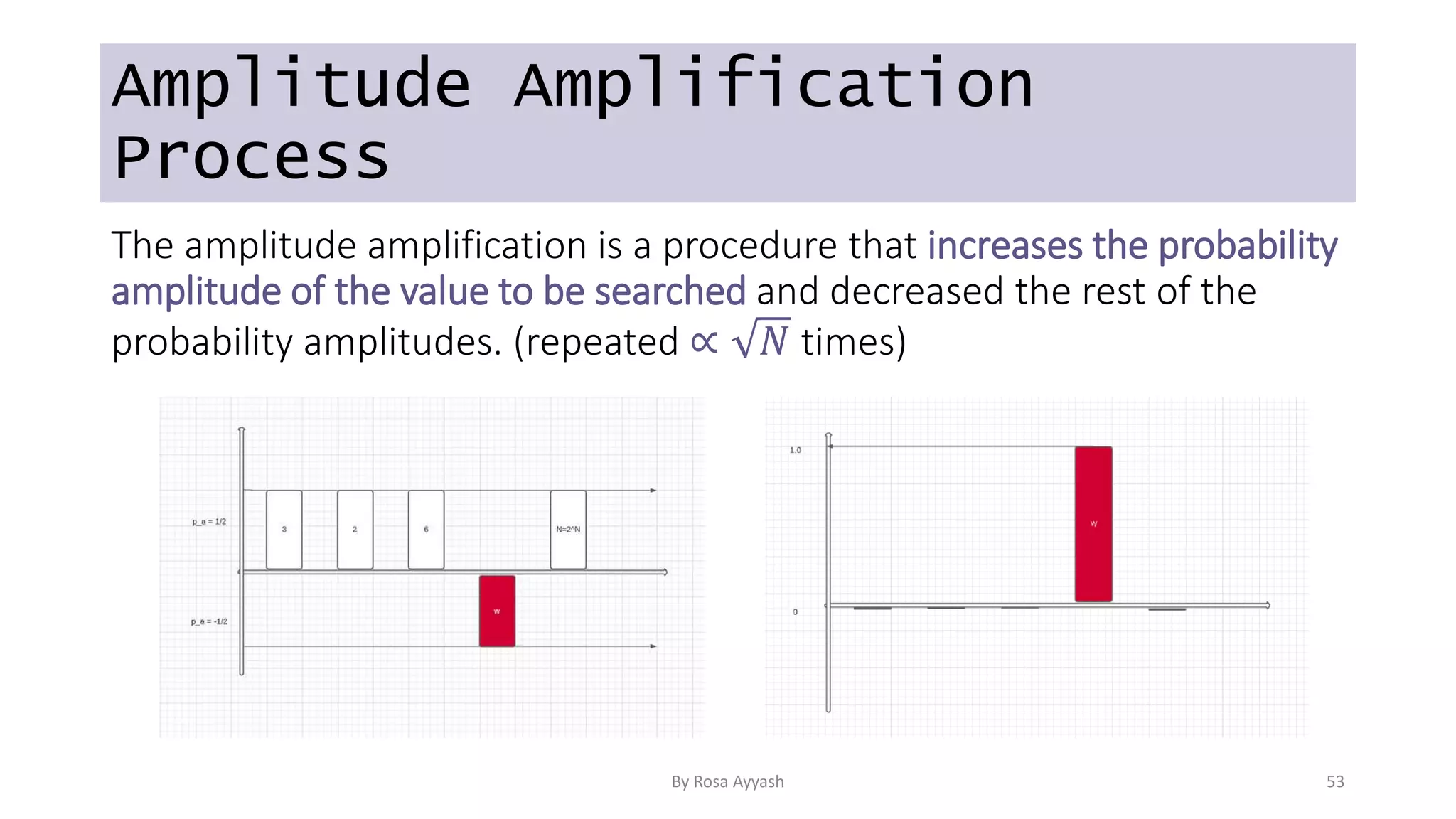
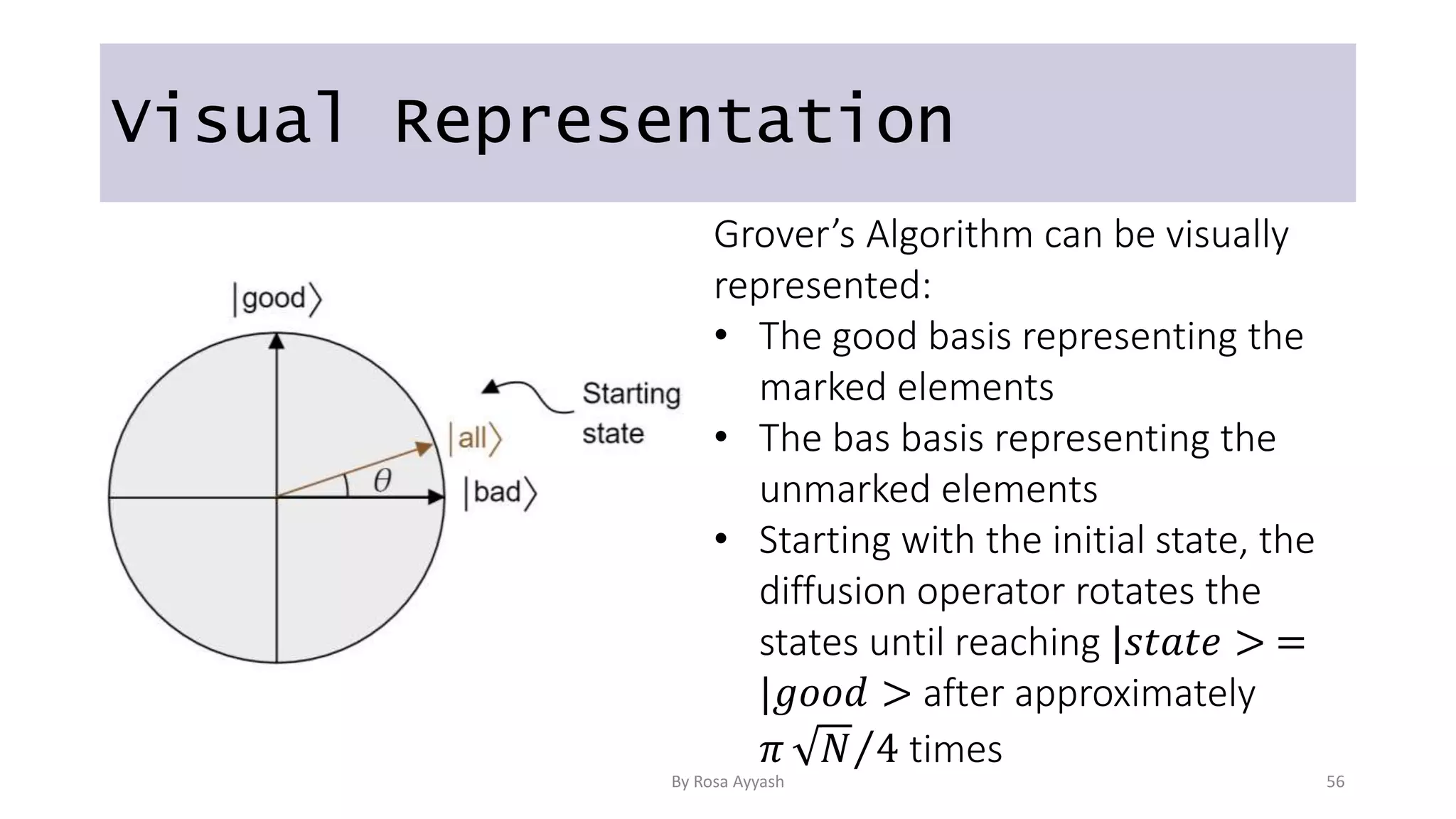
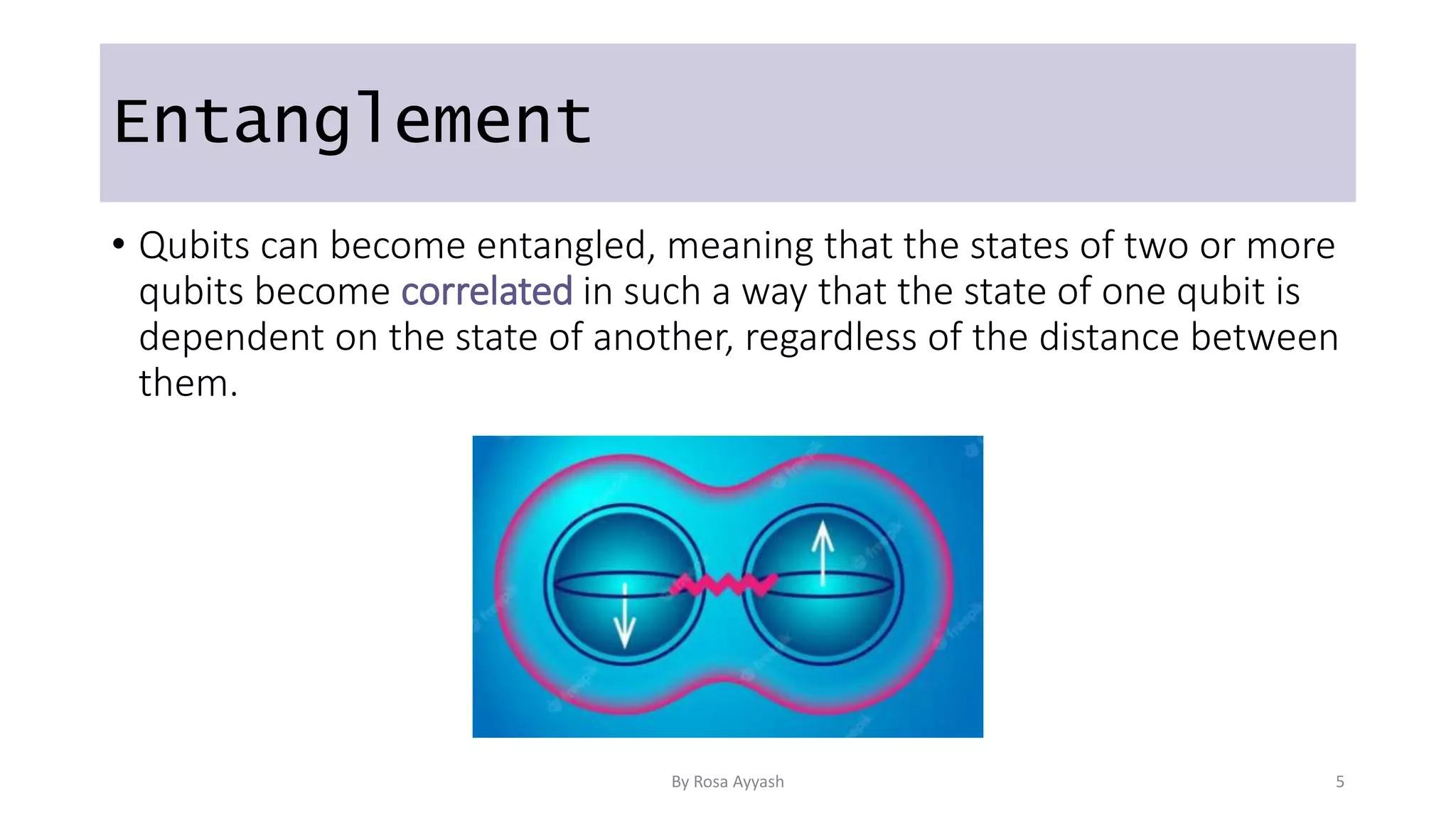
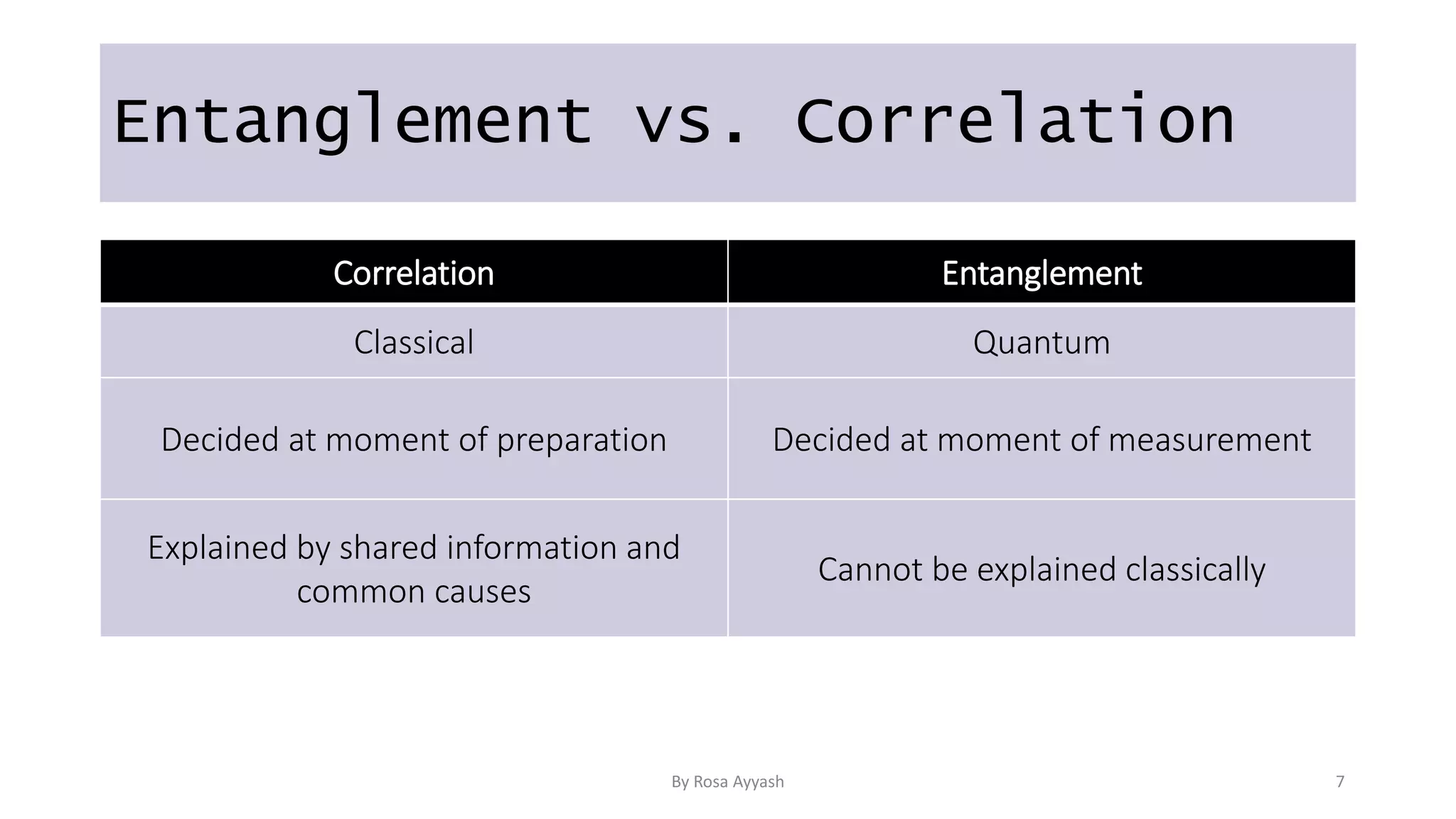
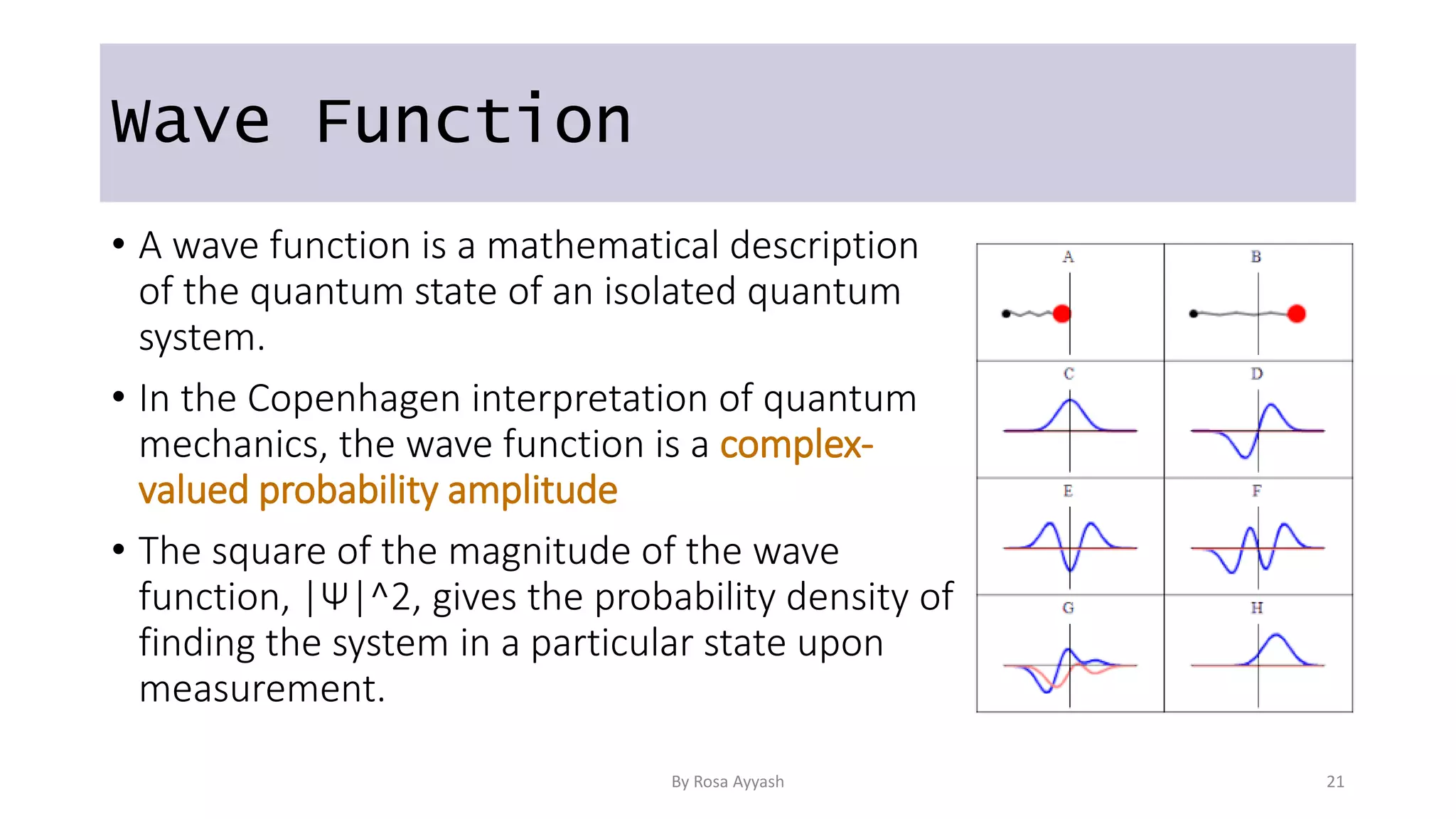
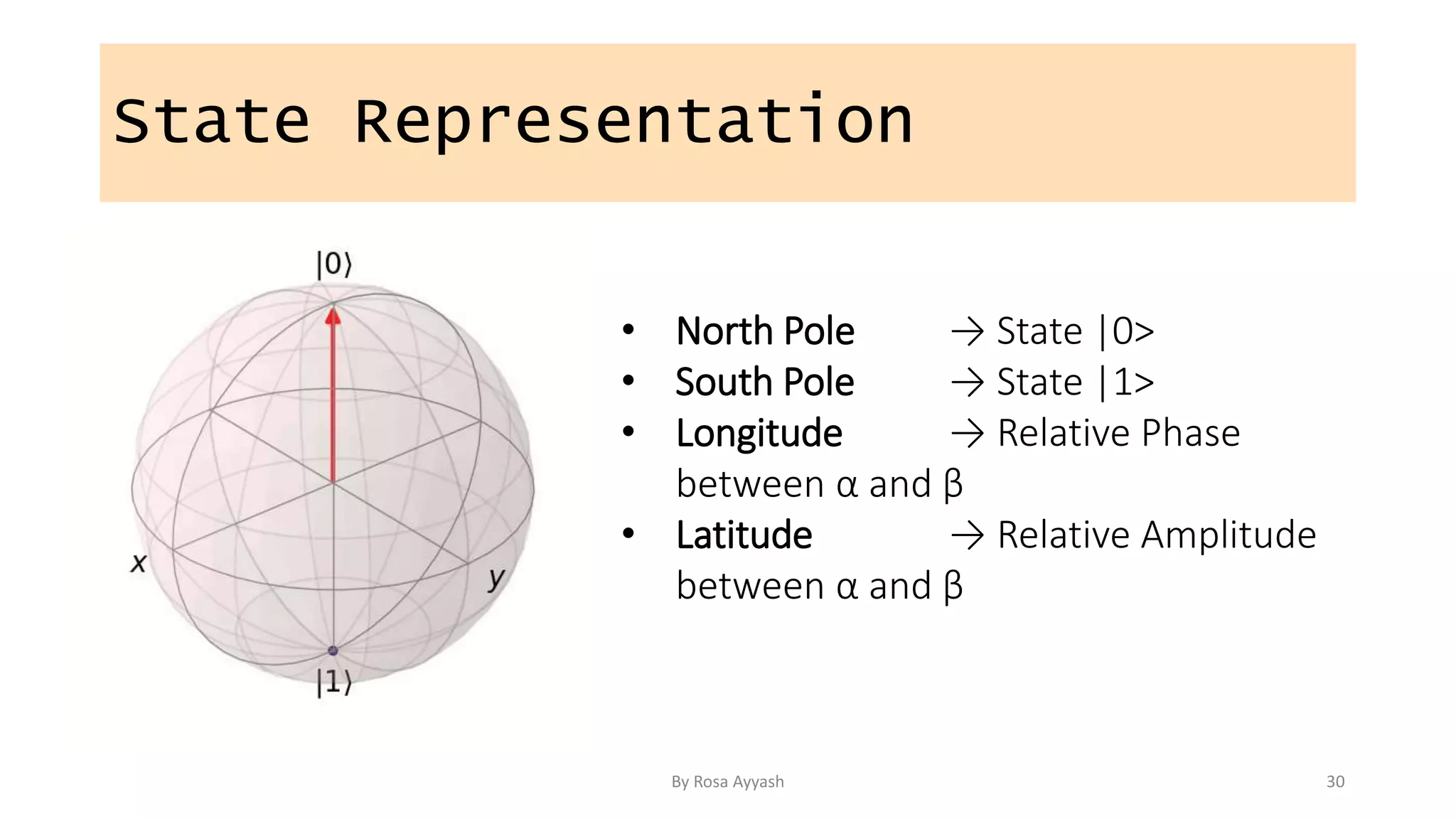
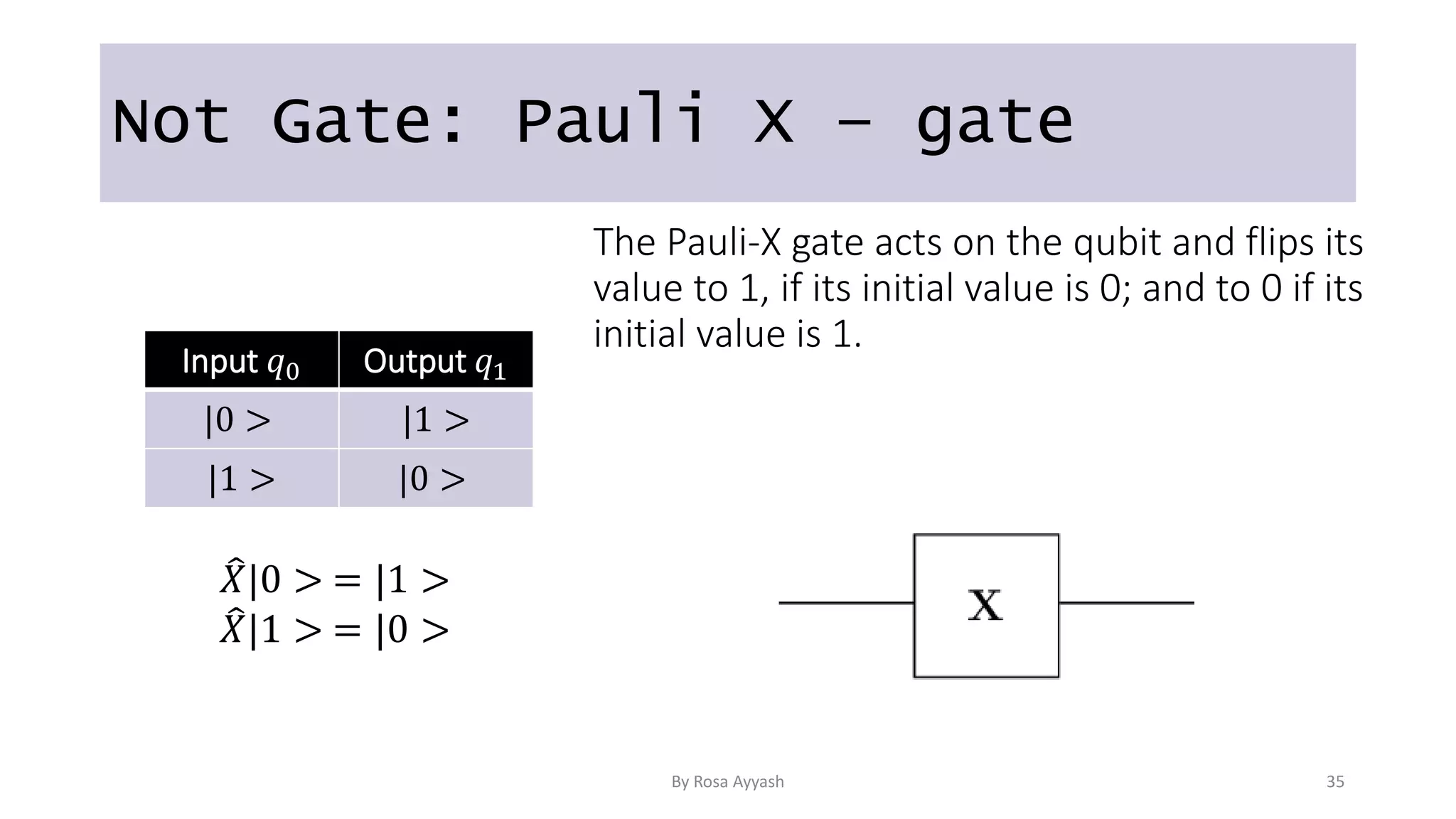
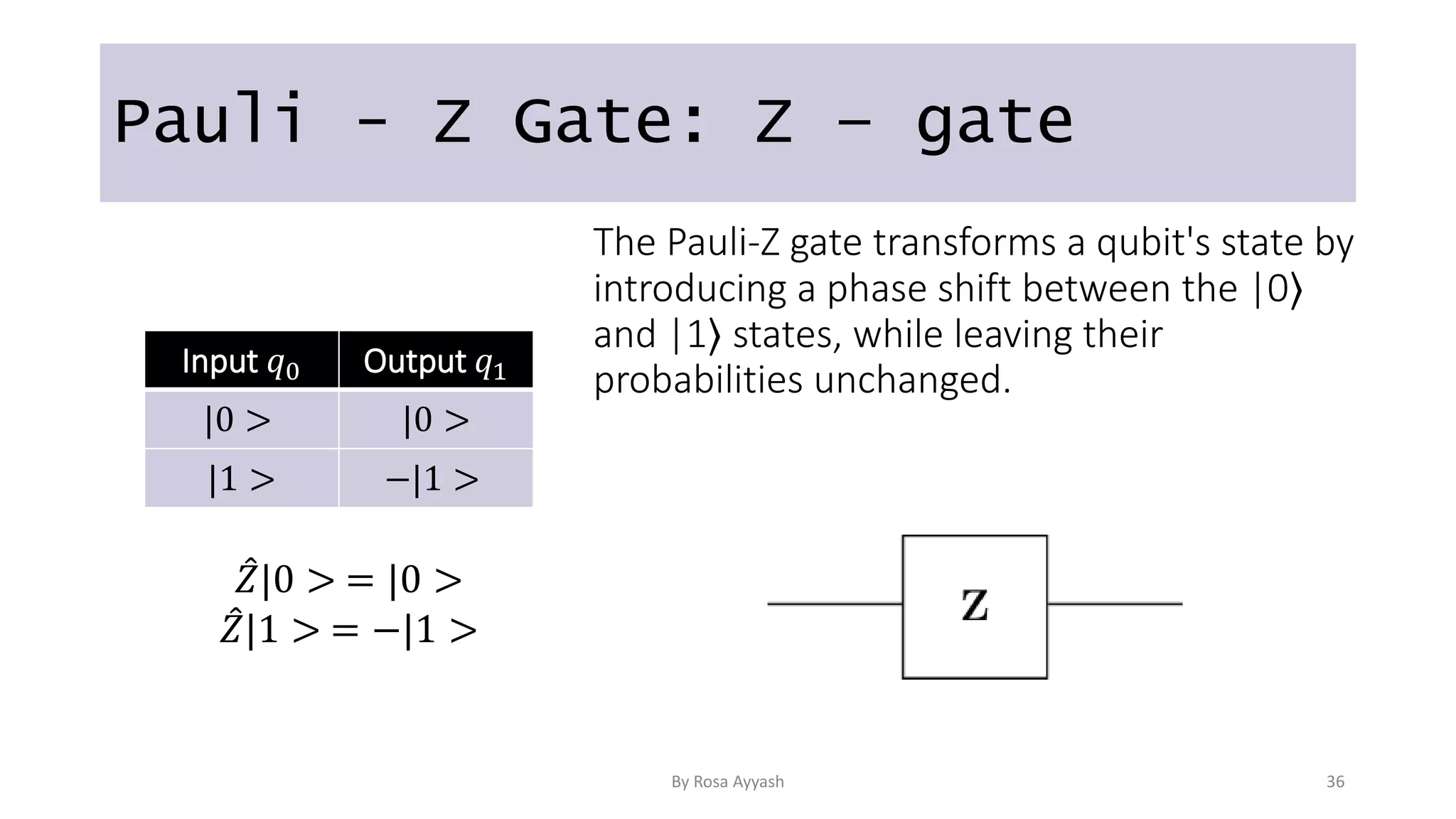
The document explains key concepts of quantum computing, focusing on qubits, superposition, entanglement, and measurement. It discusses the principles of wave-particle duality, Heisenberg's uncertainty principle, and various quantum gates like the Hadamard and CNOT gates. Additionally, it delves into quantum circuits and algorithms, highlighting algorithms like Deutsch's and Grover's, which utilize oracles for efficiency in computation.

1. Key Concepts in
Quantum Computing You
Should Know About
WOMANIUM Quantum Program 2023
By Rosa Ayyash 1

2. 1.
Qubit
By Rosa Ayyash 2

3. Quantum Bit
• A qubit, short for quantum bit, is the fundamental unit of quantum
information, analogous to the classical bit in classical computing.
• Unlike classical bits that can exist in one of two states, 0 or 1, qubits
have the unique property of being able to exist in a superposition of
both 0 and 1 states simultaneously.
• Key characteristics of qubits include:
Superposition, Entanglement,
Measurement.
By Rosa Ayyash 3

4. Superposition
• A qubit can exist in a linear combination of its
0 and 1 states.
• Mathematically, this can be represented as:
α|0⟩ + β|1⟩, where α and β are complex
numbers that determine the probability
amplitude of the qubit being in state |0⟩ or
|1⟩, respectively.
• This superposition allows qubits to represent
multiple possibilities simultaneously.
By Rosa Ayyash 4

5. Entanglement
• Qubits can become entangled, meaning that the states of two or more
qubits become correlated in such a way that the state of one qubit is
dependent on the state of another, regardless of the distance between
them.
By Rosa Ayyash 5

6. Quantum Entanglement
• Imagine two entangled electrons; their total spin must add up to zero.
• Spin is an intrinsic property of particles, akin to a tiny compass needle
that points in a specific direction.
• If Particle A has a “spin-up” along a certain axis, then Particle B must
be “spin-down" along the same axis to maintain the total spin of zero.
By Rosa Ayyash 6

7. Entanglement vs. Correlation
Correlation Entanglement
Classical Quantum
Decided at moment of preparation Decided at moment of measurement
Explained by shared information and
common causes
Cannot be explained classically
By Rosa Ayyash 7

8. Measurement
• When a qubit is measured, its superposition
collapses into one of its possible states (0 or
1), with a probability determined by the
squared magnitudes of the amplitudes α and
β.
• The act of measurement (observation)
projects the quantum state onto one of its
basis.
• It destroys the superposition, providing a
classical outcome.
By Rosa Ayyash 8

9. Bonus no.1
Particle – Wave
Duality
By Rosa Ayyash 9

10. Particle – Wave Duality
• Wave-particle duality is a fundamental concept in
quantum mechanics that describes the behavior of
subatomic particles, such as electrons and photons, as
having both wave-like and particle-like characteristics,
depending on the experimental setup and observation.
• This principle challenges classical notions of distinct
particle and wave behavior and is described
mathematically using the wave function, a mathematical
function that encodes the probability distribution of a
particle's properties.
By Rosa Ayyash 10

11. Particle Nature
• When particles are observed in
experiments involving discrete interactions,
they exhibit behaviors characteristic of
particles.
• This means they have a well-defined
position and can interact in ways similar to
classical particles.
• For example, particles can be detected at
specific points on a screen in a double-slit
experiment.
By Rosa Ayyash 11

12. Wave Nature
• When particles are in experiments involving
interference and diffraction phenomena, they
display behaviors characteristic of waves.
• This behavior is demonstrated in the double-
slit experiment, where particles are sent
through two slits and produce an interference
pattern on a screen behind the slits.
• This pattern is similar to what would be
produced by waves, like light or sound waves,
interfering with each other.
By Rosa Ayyash 12

13. The Double–Slit Experiment: Set up
• Electrons are ejected to a
double slit apparatus
• The slits should be small to
allow quantum effects
• The particles pass through the
slits and hit a screen on the
other side.
By Rosa Ayyash 13

14. The Double–Slit Experiment: Results
By Rosa Ayyash 14

15. The Double–Slit Experiment: Results
• When observed as particles, they pass through one slit or the other,
creating a pattern that matches the slit shape.
• When not observed and treated as waves, they create an interference
pattern.
• This emphasizes on the importance of observation (measurement) in a
quantum setup, as it has the capability of resetting the system and
changing its behavior.
By Rosa Ayyash 15

16. Heisenberg’s Principle
• The Heisenberg Uncertainty Principle, formulated by Werner
Heisenberg in 1927, states a fundamental limit to the precision with
which specific pairs of complementary properties of a particle can be
simultaneously known.
• Complementary properties cannot be precisely determined
simultaneously due to the wave-like nature of particles and the
mathematical relationships between these properties in the quantum
world.
By Rosa Ayyash 16

17. Heisenberg’s Principle
• The most famous pair of complementary properties described by the
uncertainty principle are position (x) and momentum (p) of a particle.
Where Δx represents the uncertainty in position, Δp represents the
uncertainty in momentum, ħ (h-bar) is the reduced Planck constant,
which is a fundamental constant of nature.
• the more precisely we know the position of a particle, the less precisely
we can know its momentum, and vice versa.
By Rosa Ayyash 17

18. Back to the Duality
• This relationship is a direct consequence
of the wave-like behavior of particles.
• When we measure the position of a
particle more precisely, we effectively
"squeeze" its wave function, causing it to
spread out in momentum space.
• Conversely, if we try to measure
momentum precisely, the wave function
gets "squeezed" in position space.
By Rosa Ayyash 18

19. 2.
Quantum State
By Rosa Ayyash 19

20. Quantum State
• The quantum state is essentially the state of knowledge about the
system. It includes all the information necessary to completely
describe the system's properties, such as its position, momentum,
energy, spin, etc.
• This means that the quantum state includes both the wave function
and additional information about the system's observable quantities.
By Rosa Ayyash 20

21. Wave Function
• A wave function is a mathematical description
of the quantum state of an isolated quantum
system.
• In the Copenhagen interpretation of quantum
mechanics, the wave function is a complex-
valued probability amplitude
• The square of the magnitude of the wave
function, |Ψ|^2, gives the probability density of
finding the system in a particular state upon
measurement.
By Rosa Ayyash 21

22. Bra - Ket Representation
• A state function is a vector in a complex vector space called Hilbert
space.
• It can be represented using various ways; one of the most common is
the Bra - Ket representation:
𝜓 > = 𝛼 1 > + 𝛽|2 >
Wave Function
Amplitude coefficient
Basis Vector
By Rosa Ayyash 22

23. Bra – Ket Representation
𝜓 > = 𝛼 1 > + 𝛽|2 >
• The probabilities for the possible results of the measurements made
on a measured system can be derived from the wave function.
• As such,
• Probability of being in state |1 > : 𝛼 2
• Probability of being in state |2 > : 𝛽 2
By Rosa Ayyash 23

24. Quantum State: Multi-qubit system
The state of multiple qubits can be represented as a combined
state using the tensor product.
e.g. Qubit 1 is in state 1 and Qubit 2 is in state 0. The combined
quantum state is written as:
|𝜑 > = |𝜑 >1⨂|𝜑 >2 = |1 > ⨂|0 > = |10 >
By Rosa Ayyash 24

25. Bonus no.2
Bloch Sphere
By Rosa Ayyash 25

26. Bloch Sphere
• The Bloch sphere is a geometrical representation of the pure
state space of a two-level quantum mechanical system, named after
the physicist Felix Bloch
• The Bloch sphere is a unit 2-sphere, with antipodal points
corresponding to a pair of mutually orthogonal state vectors.
• The points on the surface of the sphere correspond to the pure states
of the system, whereas the interior points correspond to the mixed
states.
By Rosa Ayyash 26

27. The Dimensionality
• Any pure state can be written as a combination of the basis vectors | ⟩
0
and | ⟩
1 , where the coefficient of each of the two basis vectors is a
complex number.
• The state is described by four real numbers.
• Only the relative phase between the coefficients of the two basis
vectors has a physical meaning; the state can then be represented by
only three real numbers.
• Hence, the dimensionality of the Bloch Sphere.
By Rosa Ayyash 27

28. State Representation
• The total probability of the system has to add up to 1:
𝜓(𝑥, 𝑡) 2 = 1
• With that, the state can be written as:
| ⟩
𝜓 = cos(𝜃)|0 > + 𝑒𝑖𝜙sin(𝜃)|1 >
Where 0 ≤ 𝜃 ≤ 𝜋 and 0 ≤ 𝜙 ≤ 2𝜋
• This representation is always unique; hence, the point of the Bloch
sphere represented by 𝜃 and 𝜙 is unique.
By Rosa Ayyash 28

29. State Representation
• The parameters 𝜃 and 𝜙, re-interpreted in spherical coordinates as the
colatitude with respect to the z-axis and the longitude with respect to
the x-axis.
• A point on the Bloch sphere in ℝ3:
𝑎 = (sin 𝜃 cos 𝜙 , sin 𝜃 sin 𝜙 , cos 𝜃)
By Rosa Ayyash 29

30. State Representation
• North Pole → State |0>
• South Pole → State |1>
• Longitude → Relative Phase
between α and β
• Latitude → Relative Amplitude
between α and β
By Rosa Ayyash 30

31. Rotations on the Bloch Sphere
• The rotations of the Bloch sphere about the
Cartesian axes in the Bloch basis are given by:
𝑅𝑥 𝜃 = 𝑒−𝑖𝜃𝑋/2 =
cos(𝜃 2) −𝑖 sin(𝜃 2)
−𝑖 sin(𝜃 2) cos(𝜃 2)
𝑅𝑦 𝜃 = 𝑒−𝑖𝜃𝑌/2 =
cos(𝜃 2) − sin(𝜃 2)
sin(𝜃 2) cos(𝜃 2)
𝑅𝑧 𝜃 = 𝑒−𝑖𝜃𝑍/2 = 𝑒−𝑖𝜃/2 0
0 𝑒𝑖𝜃/2
By Rosa Ayyash 31

32. 3.
Quantum Gates
By Rosa Ayyash 32

33. Quantum Gates
• Similar to classical logic gates, quantum
gates manipulate qubits to perform
quantum operations.
• Quantum gates can change the
amplitudes and phases of qubits,
allowing for complex computations
using quantum parallelism.
By Rosa Ayyash 33

34. How to Interact with the Qubit
• Quantum gates are operators that act on qubits to perform
transformations. These gates can:
- Change the qubit's state
- Create superposition
- Introduce phase shifts
- Generate entanglement.
By Rosa Ayyash 34

35. Not Gate: Pauli X – gate
Input 𝑞0 Output 𝑞1
|0 > |1 >
|1 > |0 >
The Pauli-X gate acts on the qubit and flips its
value to 1, if its initial value is 0; and to 0 if its
initial value is 1.
𝑋|0 > = |1 >
𝑋|1 > = |0 >
By Rosa Ayyash 35

36. Pauli - Z Gate: Z – gate
Input 𝑞0 Output 𝑞1
|0 > |0 >
|1 > −|1 >
The Pauli-Z gate transforms a qubit's state by
introducing a phase shift between the |0⟩
and |1⟩ states, while leaving their
probabilities unchanged.
𝑍|0 > = |0 >
𝑍|1 > = −|1 >
By Rosa Ayyash 36

37. Hadamard Gate: H – Gate
The H – gate is applied on a qubit to
create superposition.
𝐻|0 > =
1
2
|0 > +
1
2
|1 >
𝐻 1 > =
1
2
0 > −
1
2
|1 >
Input 𝑞0 Output 𝑞1
|0 > 1
2
|0 > +
1
2
|1 >
|1 > 1
2
|0 > −
1
2
|1 >
By Rosa Ayyash 37

38. Controlled NOT Gate: CX – Gate
Control 𝑞0 Target 𝑞𝟏 Output 𝑞𝟐
0 0 0
0 1 1
1 0 1
1 1 0
• The CNOT gate operates on two qubits,
often referred to as the control qubit
(C) and the target qubit (T).
• If the control qubit is 0, the state of the
target qubit is kept the same.
• If the control qubit is 1, the state of the
target qubit is flipped.
𝐶𝑋|00 > = |00 >
𝐶𝑋|01 > = |01 >
𝐶𝑋|10 > = |11 >
𝐶𝑋|11 > = |10 >
By Rosa Ayyash 38

39. 4.
Quantum Circuit
By Rosa Ayyash 39

40. Quantum Circuit
• A quantum circuit represents a sequence of quantum gates applied to
qubits to perform quantum computations.
By Rosa Ayyash 40

41. Components of a Quantum
Circuit
• Qubits: The quantum bits that the circuit operates on. They can be
initialized in specific states, manipulated, and measured.
• Quantum Gates: Quantum gates are unitary operators that perform
specific operations on qubits. These gates manipulate the state of
qubits by changing their amplitudes and phases.
• Entanglement Operations: Some gates create entanglement between
qubits (e.g. Hadamard followed by CNOT gate).
• Measurements: At specific points in the circuit, qubits are measured,
collapsing their superposition into classical states (0 or 1) with
probabilities determined by their amplitudes.
By Rosa Ayyash 41

42. 5.
Quantum Algorithms
By Rosa Ayyash 42

43. What is an algorithm?
• A step-by-step set of well-defined instructions or rules that outline
how to solve a particular problem or perform a specific task.
• Algorithms provide a systematic approach to processing input data and
producing desired output.
Input Output
ALGORITHM
By Rosa Ayyash 43

44. Oracle
• In computer science, an “Oracle” is a subroutine that can perform
specific tasks. In this case, the oracle is the mysterious function that
takes in input (0s and 1s) and gives you an output (0 or 1).
• In quantum computing, many algorithms rely on this oracle model of
computation and the aim is to solve some problem making as
minimum queries as possible.
By Rosa Ayyash 44

45. Deutsch Algorithm: Problem
We have a mysterious black box (function) that takes as input 0 and 1
and outputs 0 or 1. Our goal is to know if the function is:
• Constant: always outputting the same answer
• Balanced: outputting a different answer each time with equal
probability
By Rosa Ayyash 45

46. Deutsch Algorithm: Problem
We are provided with a function 𝑓: {0,1} → {0,1} which means
that our function 𝑓 takes as input 0 and 1 and maps it to 0 or
1. We say that 𝑓 is:
- constant if 𝑓 0 = 𝑓(1)
- balanced if 𝑓 0 ≠ 𝑓(1)
Input Output
0 0
1 0
Input Output
0 0
1 1
Example of a Constant function Example of a Constant function
By Rosa Ayyash 46

47. Deutsch Algorithm: Solution
Classical Solution
Given such a function, we need to
evaluate the function twice to get
an answer using a classical
computer.
Quantum Solution
• Since any Boolean function can be
converted to an equivalent unitary
operator 𝑈𝑓 (an oracle)
• We need to evaluate the function
only once.
• This sped up is significantly large
for higher number of inputs
(Deutsch-Jozsa Algorithm)
By Rosa Ayyash 47

48. Deutsch Algorithm: Algorithm
• Deutsch Algorithm is the quantum algorithm to solve this problem.
• We need a 2 qubit circuit
• We apply the following steps in order:
- Set the second qubit to state | ⟩
− by applying X then H gates
- Apply H to first qubit
- Apply 𝑈𝑓 (oracle)
- Apply H to first qubit
- Measure the first qubit. if it is 0, then f is constant. If it is 1,
then f is balanced.
By Rosa Ayyash 48

49. Deutsch Algorithm: Circuit
By Rosa Ayyash 49

50. Grover’s Algorithm
• Grover's algorithm is a quantum algorithm designed to perform an
unstructured search on an unordered database.
• In the worst case, a classical search algorithm might need to check
every item in the list, resulting in a time complexity of 𝑶(𝟐𝒏
) where n
is the number of items in the list.
• Grover’s algorithm provides a quadratic speed up 𝑶 𝑵 proving the
importance of quantum algorithms
By Rosa Ayyash 50

51. General Form of Grover’s
Algorithm
• Assume there are 𝑁 = 2𝑛 elements in a list L, one element is marked.
• Suppose a function 𝑓:
𝑓 𝑥 =
1 𝑖𝑓 𝑥 𝑖𝑠 𝑚𝑎𝑟𝑘𝑒𝑑
0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
• We aim to find the element(s) 𝑥 with 𝑓 𝑥 = 1
By Rosa Ayyash 51

52. Oracle: Marking the element
In this algorithm, the oracle serves to mark the element in search.
Say we are searching for the w element from the following n-list of
numbers: [4,6,8,…, w, … ].
⟶ The oracle marks the element w by flipping the sign of its amplitude
(phase kickback).
By Rosa Ayyash 52

53. Amplitude Amplification
Process
The amplitude amplification is a procedure that increases the probability
amplitude of the value to be searched and decreased the rest of the
probability amplitudes. (repeated ∝ 𝑁 times)
By Rosa Ayyash 53

54. Grover’s Diffusion Operator
• The amplitude amplification process is done using Grover’s diffusion
operator.
• The purpose of the Diffusion Operator is to magnify the amplitude of
the state representing the marked item in the superposition, while
simultaneously decreasing the amplitudes of the other states.
• The Diffusion operator involves two steps:
- Amplitude Amplification
- Equal Amplitude Inversion
By Rosa Ayyash 54

55. Grover’s Diffusion Operator:
Mathematical Formulation
• The uniform superposition of all states is given by:
| ⟩
𝑠 =
1
𝑁 𝑥=1
𝑁−1
| ⟩
𝑥 where 𝑥 𝜖 {0,1}
• The inversion operator is as follows:
𝑍0 = 2 ⟩
𝑠 𝑠 − 𝐼
• In terms of gates, the Grover diffusion operator is:
𝐷 = − 𝐻⨂𝑛
𝑍0𝐻⨂𝑛
By Rosa Ayyash 55

56. Visual Representation
Grover’s Algorithm can be visually
represented:
• The good basis representing the
marked elements
• The bas basis representing the
unmarked elements
• Starting with the initial state, the
diffusion operator rotates the
states until reaching |𝑠𝑡𝑎𝑡𝑒 > =
|𝑔𝑜𝑜𝑑 > after approximately
𝜋 𝑁 4 times
By Rosa Ayyash 56

57. The Algorithm
• Apply the Hadamard gate to all qubits
• Inverse the marked element using the oracle
• Apply the diffusion operator
• Iterate the algorithm for ≈ 𝜋 𝑁 4 times to get the marked element
with a small probability of error
1
2𝑛
• Measure all qubits
By Rosa Ayyash 57

58. References
By Rosa Ayyash 58

59. By Rosa Ayyash 59
From Womanium YT Channel
• https://youtu.be/IckuVjd89-g?list=PL_wGNAk5B0pUVk2G7VvjHWA-P_uorDB7X
• https://youtu.be/Ezm3TIBEjfE?list=PL_wGNAk5B0pUVk2G7VvjHWA-P_uorDB7X
• https://youtu.be/f5vDf1V-g14?list=PL_wGNAk5B0pUVk2G7VvjHWA-P_uorDB7X
• https://youtu.be/E_XxrBcBFQw?list=PL_wGNAk5B0pUVk2G7VvjHWA-P_uorDB7X
• https://youtu.be/uJCrzhr4iek?list=PL_wGNAk5B0pUVk2G7VvjHWA-P_uorDB7X

60. References
By Rosa Ayyash 60
• https://gitlab.com/qworld/nickel/-/tree/master/nickel
• https://gitlab.com/qworld/bronze-qiskit/-/tree/master/quantum-with-qiskit?ref_type=heads
• https://learning.quantum-computing.ibm.com/tutorial/composer-user-guide
• https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Ph
ysical_Chemistry_(LibreTexts)/04%3A_Postulates_and_Principles_of_Quantum_Mechanics/4.01%3
A_The_Wavefunction_Specifies_the_State_of_a_System
• https://byjus.com/physics/wave-
function/#:~:text=In%20quantum%20physics%2C%20a%20wave,Greek%20letter%20called%20psi
%2C%20%F0%9D%9A%BF
• https://physics.stackexchange.com/questions/313959/visual-interpretation-on-the-bloch-sphere-
when-hadamard-gate-is-applied-twice
• https://towardsdatascience.com/grovers-search-algorithm-simplified-4d4266bae29e
• BORN, M. Physical Aspects of Quantum Mechanics. Nature 119, 354–357 (1927).
https://doi.org/10.1038/119354a0
• https://www.damtp.cam.ac.uk/user/tong/relativity.html