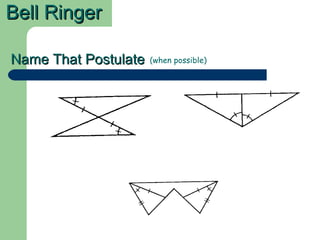
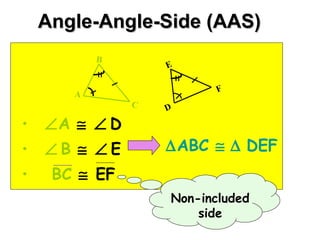
The document discusses three postulates for triangle congruence: 1) Angle-Side-Angle (ASA) postulate - If two angles and the included side of one triangle are congruent to another triangle, then the triangles are congruent. 2) Angle-Angle-Side (AAS) postulate - If two angles and a non-included side of one triangle are congruent to another, then the triangles are congruent. 3) Side-Side-Side (SSS) postulate - If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.

1. (when possible) Bell Ringer Name That Postulate

2. Angle – Side – Angle Postulate - If two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent.

3. Angle-Side- Angle (ASA)  A   D AB  DE  B   E  ABC   DEF B A C E D F included side

4. The side between two angles Included Side GI HI GH

5. Name the included side:  Y and  E  E and  S  S and  Y Included Side YE ES SY S Y E

6. Angle – Angle – Side Postulate - If two angles and a non-included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent.

7. Angle-Angle-Side (AAS)  A   D  B   E BC  EF  ABC   DEF B A C E D F Non-included side

8. Warning: No SSA Postulate A C B D E F NOT CONGRUENT There is no such thing as an SSA postulate!

9. Warning: No AAA Postulate A C B D E F There is no such thing as an AAA postulate! NOT CONGRUENT

10. Name That Postulate SAS ASA SSS SSA (when possible)

11. Let’s Practice Indicate the additional information needed to enable us to apply the specified congruence postulate. For ASA: For SAS:  B   D For AAS:  A   F AC  FE

12. You try! Indicate the additional information needed to enable us to apply the specified congruence postulate. For ASA: For SAS: For AAS: