Downloaded 13 times
Uploaded byАркадий Захаров
лек. 4 строение атома ч.1
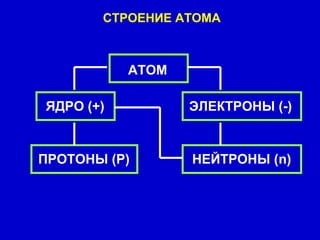
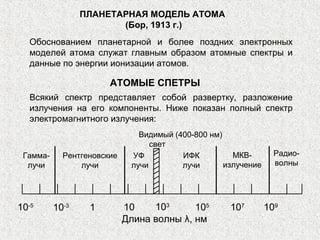
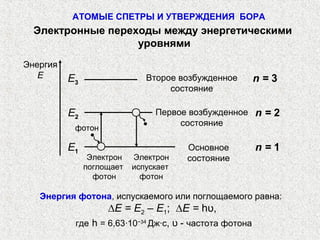
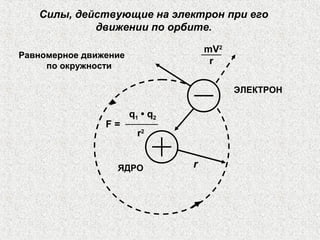
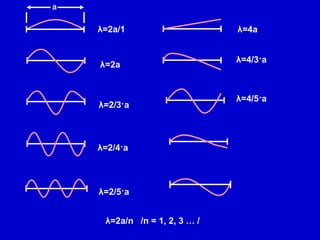
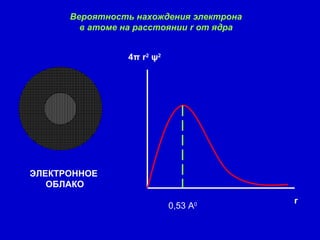
Документ описывает модели строения атома, включая модель 'сливового пудинга' Томсона, ядерную модель Резерфорда и планетарную модель Бора. В нем также представлены концепции атомного спектра, квантования энергии, корпускулярно-волновой двойственности и принципа неопределенности. Основное внимание уделяется уравнению Шредингера и волновым функциям, описывающим движение электронов в атоме.
More Related Content
Similar to лек. 4 строение атома ч.1
лек. 4 строение атома ч.1
- 1. СТРОЕНИЕ АТОМА. АТОМНЫЕМОДЕЛИ 1. Модель «сливового пудинга» (Томсон, 1904 г.) 2. Ядерная модель атома (Резерфорд, 1911 г.) 3. Планетарная модель атома (Бор, 1913 г.)
- 2. Лекция № 4 СТРОЕНИЕАТОМА 1.Опыты Резерфорда. Ядерная модель атома. Источник α-частиц d=6·10-5 см Э
- 3. СТРОЕНИЕ АТОМА АТОМ ЯДРО (+)ЭЛЕКТРОНЫ (-) ПРОТОНЫ (Р) НЕЙТРОНЫ (n)
- 4. СТРОЕНИЕ АТОМА ЧАСТИЦА ЗАРЯД МАССА Кле.з.э. г. а.е.м. е.м.э. ЭЛЕКТРОН ē -1,6·10-19 -1 9,11·10-28 5,49·10-4 1 ПРОТОН НЕЙТРОН р n 1,6·10-19 +1 0 0 1,673·10-24 1,675·10-24 1,007276 1,008665 1836 1839 а.е.м. = 1/12 массы изотопа углерода 6 12 С Z + N = A Z = число протонов = число электронов = порядковый номер N = число нейтронов = A – Z A = массовое число ядра /атома/.
- 5. ПЛАНЕТАРНАЯ МОДЕЛЬ АТОМА (Бор,1913 г.) Обоснованием планетарной и более поздних электронных моделей атома служат главным образом атомные спектры и данные по энергии ионизации атомов. АТОМЫЕ СПЕТРЫ Всякий спектр представляет собой развертку, разложение излучения на его компоненты. Ниже показан полный спектр электромагнитного излучения: 10-5 10-3 1 10 103 105 107 109 Видимый свет Гамма- лучи Рентгеновские лучи МКВ- излучение ИФК лучи УФ лучи Радио- волны (400-800 нм) Длина волны λ, нм
- 6. НЕПРЕРЫВНЫЕ И ДИСКРЕТНЫЕСПЕКТРЫ ИЗЛУЧЕНИЯ 1. Непрерывный (сплошной) спектр - Это спектр, содержащий излучение со всеми длинами волн в пределах некоторого диапазона. Примером сплошного спектра является видимый свет. 2. Дискретный спектр – это спектр, в котором недостает излучения с определенными длинами волн. Примером такого спектра является атомный спектр поглощения (или испускания). Если пучок белого света пропустить через газообразный образец какого-либо элемента, то в прошедшем через образец пучке света будет недоставать излучения с определенными длинами волн. Спектр такого излучения называется атомным спектром поглощения. При нагревании газообразного образца до высок. темп. Он будет испускать излучение с определенными длинами волн - атомный спектр испускания.
- 7. АТОМЫЕ СПЕТРЫ ИУТВЕРЖДЕНИЯ БОРА Объясняя дискретный характер атомных спектров поглощения или испускания, Бор предположил, что между линиями атомного спектра и энергиями электронов в атомах существует соответствие. Он утверждал, что электрон в атоме не может иметь произвольных значений энергии в диапазоне непрерывного изменения, а должен иметь только определенные фиксированные значения энергии. Эти значения энергии Бор назвал дискретными, или квантовыми уровнями. Каждому такому значению энергии Бор приписал определенное число, которое он назвал квантовым числом.
- 8. АТОМЫЕ СПЕТРЫ ИУТВЕРЖДЕНИЯ БОРА Электронные переходы между энергетическими уровнями Е1 Е2 Е3 • • Электрон испускает фотон n = 2 n = 3 n = 1 Электрон поглощает фотон Основное состояние Первое возбужденное состояние Второе возбужденное состояние фотон Энергия Е Энергия фотона, испускаемого или поглощаемого равна: ∆Е = Е2 – Е1; ∆Е = hʋ, где h = 6,63·10−34 Дж·с, ʋ - частота фотона
- 9. Схема уровней энергиии квантовые переходы электрона атома водорода n=1 n=∞ n=5 n=4 n=3 n=2 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 серия Лаймана серия Бальмера серия Пашена
- 10. Схема уровней энергиии квантовые переходы электрона атома водорода n=1 n = ∞ n = 5 n = 4 n = 3 n = 2 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 серия Лаймана серия Бальмера серия Пашена
- 11. СХЕМА УРОВНЕЙ ЭНЕРГИИИ КВАНТОВЫЕ ПЕРЕХОДЫ ЭЛЕКТРОНА АТОМА ВОДОРОДА Расположение линий в спектре водорода подчиняется определенной закономерности: волновые числа могут быть выражены в виде произведения двух чисел, одно из которых равно 1,097·107 , а другое – дробь /разность двух дробей/. 1 _ 1 1 серия Лаймена = ν = R · – m = 2, 3, 4, 5, 6 … λ 12 m2 1 _ 1 1 серия Бальмера = ν = R · – m = 3, 4, 5, 6 … λ 22 m2
- 12. 1 _ 11 серия Пашена = ν = R · – m = 4, 5, 6 … λ 32 m2 1 _ 1 1 серия Брекетта = ν = R · – m = 5, 6 … λ 42 m2 1 _ 1 1 серия Пфунда = ν = R · – m = 6 … λ 52 m2 1 _ 1 1 = ν = R · – λ n2 m2
- 13. Силы, действующие наэлектрон при его движении по орбите. Равномерное движение по окружности q1 • q2 F = r2 ЯДРО ЭЛЕКТРОН mV2 r r
- 14. Силы, действующие наэлектрон при его движении по орбите. Равномерное движение по окружности ЭЛЕКТРОН ЯДРО mV2 r r F = q1 • q2 r2
- 15. АТОМ БОРА 1.Первый постулат:электрон может вращаться вокруг ядра не по любым, а по некоторым определенным, пребывая на которых он не теряет энергии h m • V • r = n /1/ 2π 2. Второй постулат: поглощение и испускание энергии атомом происходят при переходах электрона из одного квантового состояния в другое ΔE = hν /2/ По законам классической механики: при движении электрона по круговой орбите должно выполняться условие: mV2 q1 • q2 = /3/ r r2 Центробежная сила = сила электростатического притяжения.
- 16. АТОМ БОРА Из уравнений/1/ и /3/ Бор получил формулу для расчета радиусов дозволенных орбит: n2 h2 r = /4/ 4 π2 m e2 Для расчета энергии электрона в атоме – Бор воспользовался определениями кинетической энергии частицы: mV2 К.Э. = 2 и потенциальной энергии электрона q1 • q2 (– е) • е e2 П.Э. = = = r r r
- 17. АТОМ БОРА полная энергияэлектрона равна: Е = К.Э. + П.Э., т.е. mV2 e2 Е = – 2 r отсюда с помощью уравнений /3/ и /4/ получим: 2 π2 m e4 E = – /5/ n2 h2
- 18. АТОМ БОРА Уравнение /5/и/2/ позволило Бору вычислить частоты линий спектра водорода: Е2 – Е1 2 π2 m e4 1 1 ν = = – h h2 n1 2 n2 2 так как ν = С / λ, то 1 2 π2 m e4 1 1 = = – /6/ λ h2 · С n1 2 n2 2 Из этого уравнения Бор теоретически рассчитал постоянную Ридберга: 2 π2 · m · e4 R = = 109737, 3 см-1 h3 · С /109677, 58 см–1 – экспериментальное значение/
- 19. Бор, таким образом,установил смысл целых чисел n и m в уравнении Ридберга: эти числа указывают номера исходного и конечного энергетических уровней, между которыми осуществля- ется переход электрона при поглоще- нии или испускании света. АТОМ БОРА
- 20. МОДЕЛЬ АТОМА ПОБОРУ 1.3. ΔЕ = hν – постулат Планка – ядерная модель атома 1.2. r r2 mV2 q1 · q2 = 1 1 1 λ n2 m2 = R1.1. – – уравнение Ридберга 1. Факты, известные до Бора:
- 21. 2. Постулаты Бора –квантовый момент количества движения – переход электрона с орбиты на орбиту 2.1. m·V·r = n·(h/2π) 2.2. h·ν = Е2 – Е1
- 22. МОДЕЛЬ АТОМА ПОБОРУ Воспользовавшись определениями кинетической энергии частицы (К.Э. = mV2 /2) и потенциальной энергии электрона (П.Э. = –е2 /r), Бор получил следущие уравнения: 3.1. n2 h2 3.2. К К = 2π2 m e4 / h2 r = ; Е = – n = 1, 2, 3, 4 … 4π2 m e4 n2 3.1. 1 К 1 1 К 2π2 m e4 = – ; R = = = 1,0978·107 м-1 λ h·e n2 m2 h·e h3 ·e Ron = 1,0968·107 м-1 3. Уравнения, полученные Бором:
- 23. Воспользовавшись определениями кинетической энергиичастицы (К.Э. = mV2/2) и потенциальной энергии электрона (П.Э. = –е2/r), Бор получил следущие уравнения: МОДЕЛЬ АТОМА ПО БОРУ 3. Уравнения, полученные Бором: 3.1 n2 h2 4π2 me4 r = 3.2. Е = – К n2 n = 1, 2, 3, 4 … 1 λ = К he 1 1 n2 m2 – R =; К he = 2π2 me4 h3 ·e = 1,0978·107 м-1 = 3.3 2π2 me4 h2 К =; Ron = 1,0968·107 м-1
- 24. КВАНТОВАЯ МОДЕЛЬ АТОМА Современнаятеория строения атома основана на трех важнейших представлениях: 1. Квантование энергии. 2. Волновой характер движения микрочастиц (корпускулярно – волновая двойственность). 3. Вероятностный метод описания микрообъектов (принцип неопределенности). КВАНТОВАНИЕ ЭНЕРГИИ. Планк (1900 г.), Энштейн (1905 г.) Е = h · ν h – постоянная Планка = 6,63 · 10 -34 Дж·с λ · ν = с с – скорость света = 3 · 108 м/с
- 25. КВАНТОВАЯ МОДЕЛЬ АТОМА КОРПУСКУЛЯРНО– ВОЛНОВАЯ ДВОЙСТВЕННОСТЬ. Свет (и другие электро – магнитные излучения), обладает как свойствами (дифракция, интерференция), так и свойствами частицы (явление фотоэффекта, уменьшение массы Солнца на 1,5 · 1017 кг/год ). В 1924 г. Луи де Бройль выдвинул гипотезу, что с каждым движущимся материальным объектом связан волновой процесс, длина волны которого определяется по формуле: h λ = mV m – масса частицы; V – скорость частицы; h = 6,63 · 10 -34 Дж·с
- 26. КОРПУСКУЛЯРНО – ВОЛНОВАЯДВОЙСТВЕННОСТЬ. КВАНТОВАЯ МОДЕЛЬ АТОМА Для электрона: m = 9,1· 10 –31 кг; V = 1,2 · 108 м/с 6,63 · 10 –34 λ = = 0,6 · 10 –11 /м/ 9,1· 10 –31 ·1,2·108 Для пули: m = 25 г; V = 900 м/с 6,63 · 10 –34 λ = = 2,9 · 10 –35 /м/ !!! 25 · 10–3 · 9·102
- 27. КВАНТОВАЯ МОДЕЛЬ АТОМА ПРИНЦИПНЕОПРЕДЕЛЕННОСТИ (ГЕЙЗЕНБЕРГ, 1927 Г.) Двойственную природу микрочастиц объясняет принцип неопределенности: невозможно одновременно определить и скорость /или импульс Р = m·V/ и положение микрочастицы /ее координаты/: h ΔX · ΔV > 2π·m Произведение неопределенностей положения ΔX и скорости ΔV не может быть меньше чем h / 2π·m
- 28. ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ (ГЕЙЗЕНБЕРГ,1927 Г.) (продолжение) Например: Неопределенность в положении электрона, движущегося со скоростью 9 · 106 м/с, составит: 6,63 · 10 –34 λ = = 0,6 · 10–10 м 2· 3,14 · 9,1 · 10–31 · 9·106 при размере атома порядка 10–10 В то же время неопределенность в положении автомашины: m = 1 т; V = 100 км/час – составляет: 6,63 · 10–34 · 3600 ΔX = = 3,8 · 10 –39 м 2 · 3,14 · 103 · 105
- 29. ФОТОНИмпульс электрона изменяется вмомент столкновения ЯДРО КВАНТОВАЯ МОДЕЛЬ АТОМА ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ (ГЕЙЗЕНБЕРГ, 1927 Г.)
- 30. Квантование энергии, волновойхарактер движения микрочастиц и принцип неопределенности показывают, что представление о движении электрона вокруг ядра по определенным орбитам, подобно движению планет вокруг Солнца, следует считать несостоятельным. В действительности, движение электрона в атоме носит вероятностно – волновой характер. Все, что можно сказать о положении электрона в атоме – это только вероятность его нахождения в какой-либо области пространства вблизи ядра. КВАНТОВАЯ МОДЕЛЬ АТОМА ВОЛНОВЫЕ СВОЙСТВА ЭЛЕКТРОНА
- 31. Квантовая механика описываетдвижение электрона в атоме при помощи так называемой волновой функции ψ. Общий вид этой функции находится из уравнения Шредингера, которое связывает волновую функцию ψ с потенциальной энергией электрона /U/ и его полной энергией /Е/ d2 ψ d2 ψ d2 ψ 8 π2 m + + + (E – U)ψ = 0 d x2 d y2 d z2 h2 КВАНТОВАЯ МОДЕЛЬ АТОМА УРАВНЕНИЕ ШРЕДИНГЕРА
- 32. УРАВНЕНИЕ ШРЕДИНГЕРА Уравнения известныедо Шредингера: 1. Уравнение колебаний струны: d2 А 4 π2 + • А = 0 d x2 λ2 2. Уравнение де Бройля: λ = h / mV В 1926 г. Шредингер предположил: Раз электрон обладает волновыми свойствами, значит его движение в атоме можно описать волновым уравнением, подобно тому, как описываются световые и звуковые волны, колебания струны и др.:
- 33. УРАВНЕНИЕ ШРЕДИНГЕРА (продолжение) d2 ψ d2 ψd2 ψ 8 π2 m + + + (E – U)·ψ = 0 d x2 d y2 d z2 h2 Рассуждения Шредингера: К.Э. = Полная энергия – П.Э. T = E – U = mV2 / 2m; λ = √ h / 2m /E – U/ d2 ψ 8 π2 m + (E – U) ψ ; d x2 h2
- 34. УРАВНЕНИЕ КОЛЕБАНИЙ СТРУНЫ(СТОЯЧАЯ ВОЛНА) А А0 α А = А0 · sinα Р X MO /t/ /t'/ X амплитуда для точки М: X d2 А 4 π2 А = А0 · sin2π ν·t – или = – А λ d x2 λ2
- 35. а λ=2а/1 λ=2а λ=2/3·а λ=2/4·а λ=2/5·а λ=2а/n /n =1, 2, 3 … / λ=4а λ=4/3·а λ=4/5·а
- 36. 2πr = n·λ n=4n=5 n=4·1/3 несогласованность Λ = 2а/n (n = 1, 2, 3 …)
- 37. Волновая функция ψ,являющаяся решением уравнения Шредингера, назвается атомной орбиталью (АО). Физический смысл ψ – функции состоит в следущем: квадрат волновой функции (ψ2 ) определяет плотность вероятности нахожде- ния электрона в некоторой точке с координатами (x; y; z). Это означает, что вероятность нахождения частицы (электрона) в небольшом элементе объема dV вокруг точки (x; y; z) определяется произведением: ВОЛНОВАЯ ФУНКЦИЯ ψ2 ·dV
- 38. Из уравнения Шредингераследует, что атомную орбиталь можно однозначно описать тремя параметрами: Ψ = Ψ (n, l, m) эти параметры получили название квантовых чисел. ВОЛНОВАЯ ФУНКЦИЯ (продолжение) Определяя значение ψ – функции, удовлетво- ряющей уравнению Шредингера, мы находим то околоядерное пространство, в котором с наибольшей вероятностью пребывает электрон. Это околоядерное пространство и есть атомная орбиталь.
- 39. Вероятность нахождения электрона ватоме на расстоянии r от ядра ЭЛЕКТРОННОЕ ОБЛАКО 0,53 A0 r 4π r2 ψ2
- 40. Радиальное распределение вероятностинахождения W электрона (электронной плотности) на расстоянии r от ядра. Вероятность нахождения электрона в атоме на расстоянии r от ядра S = 4π r2 ΔV = 4π r2 · Δr W 4π r2 ψ2 r + Δr r ΔV
- 41. n=1 n=2 n=3 Вероятностьнахождения электрона в атоме на расстоянии r от ядра 4π r2 ψ2 r, н.м. 2S 2P 3S 3P 3d