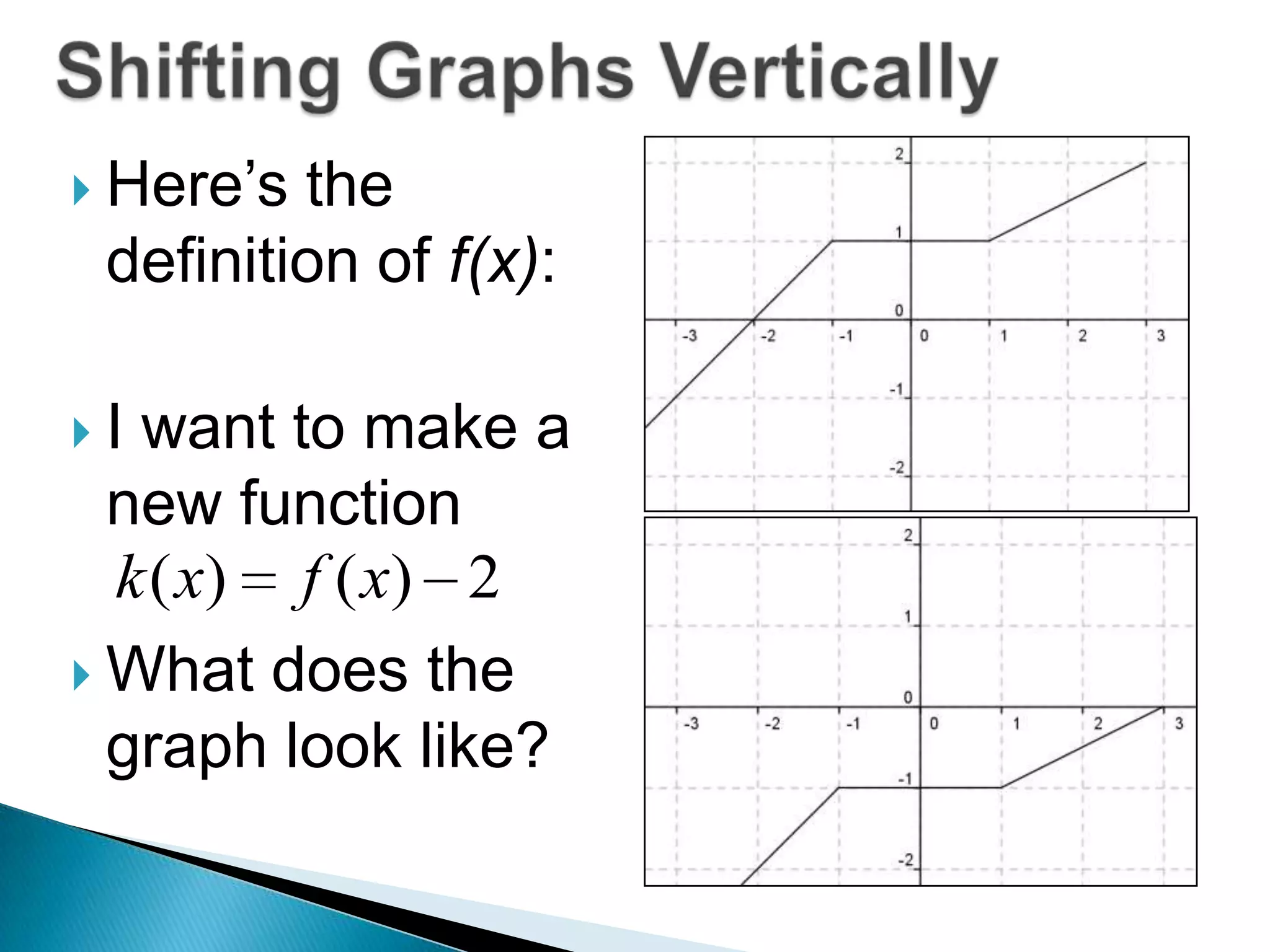
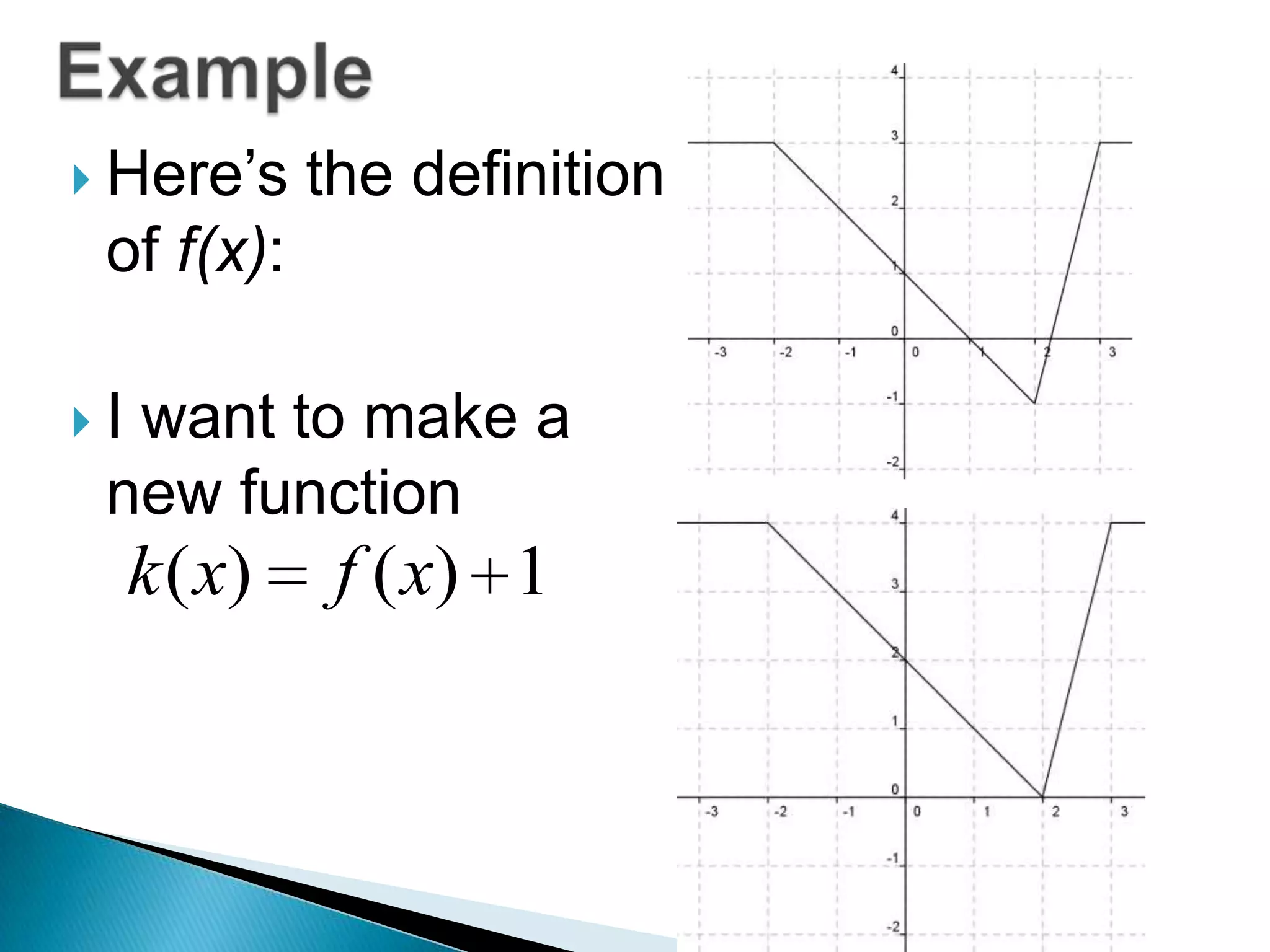
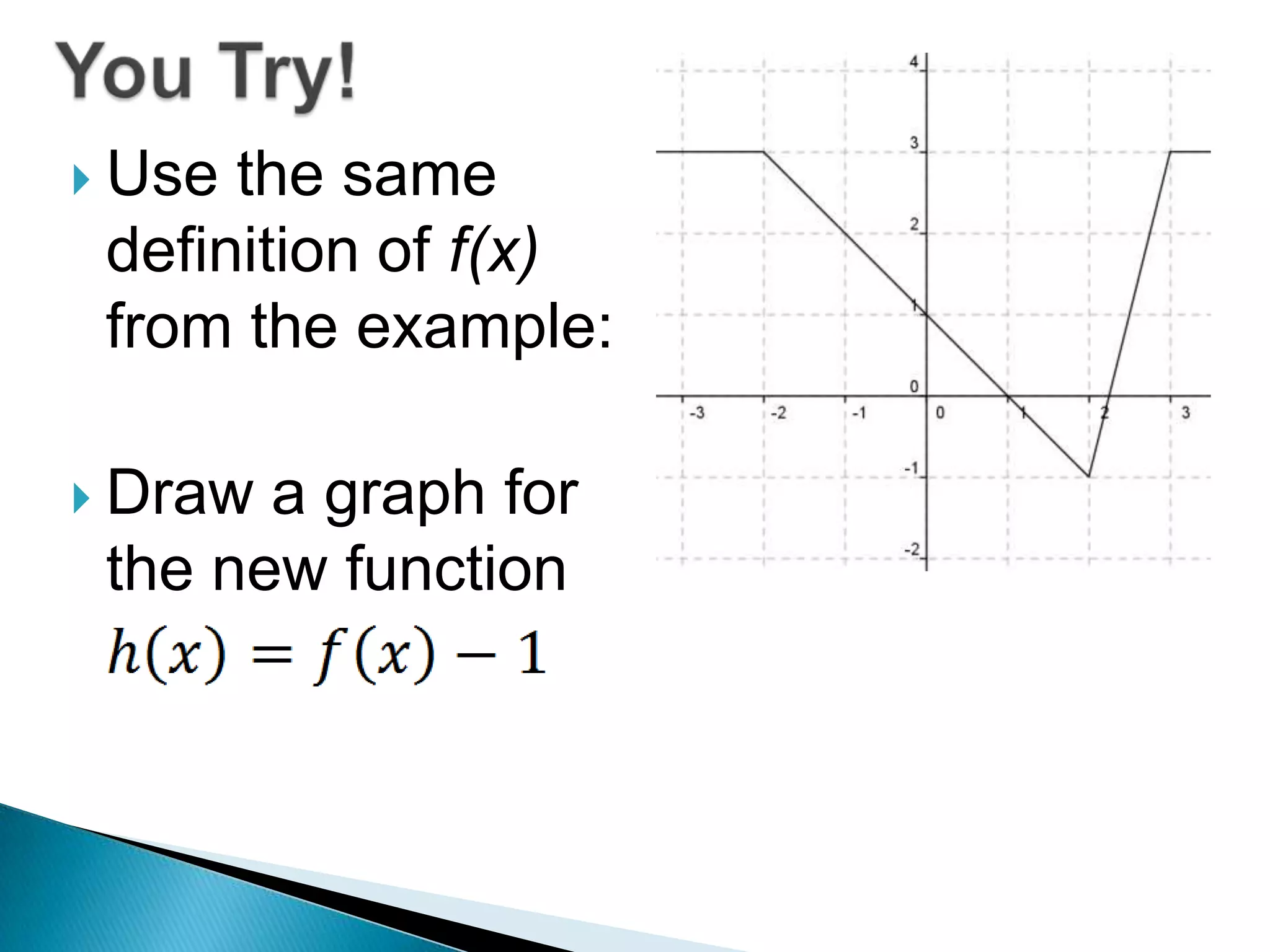
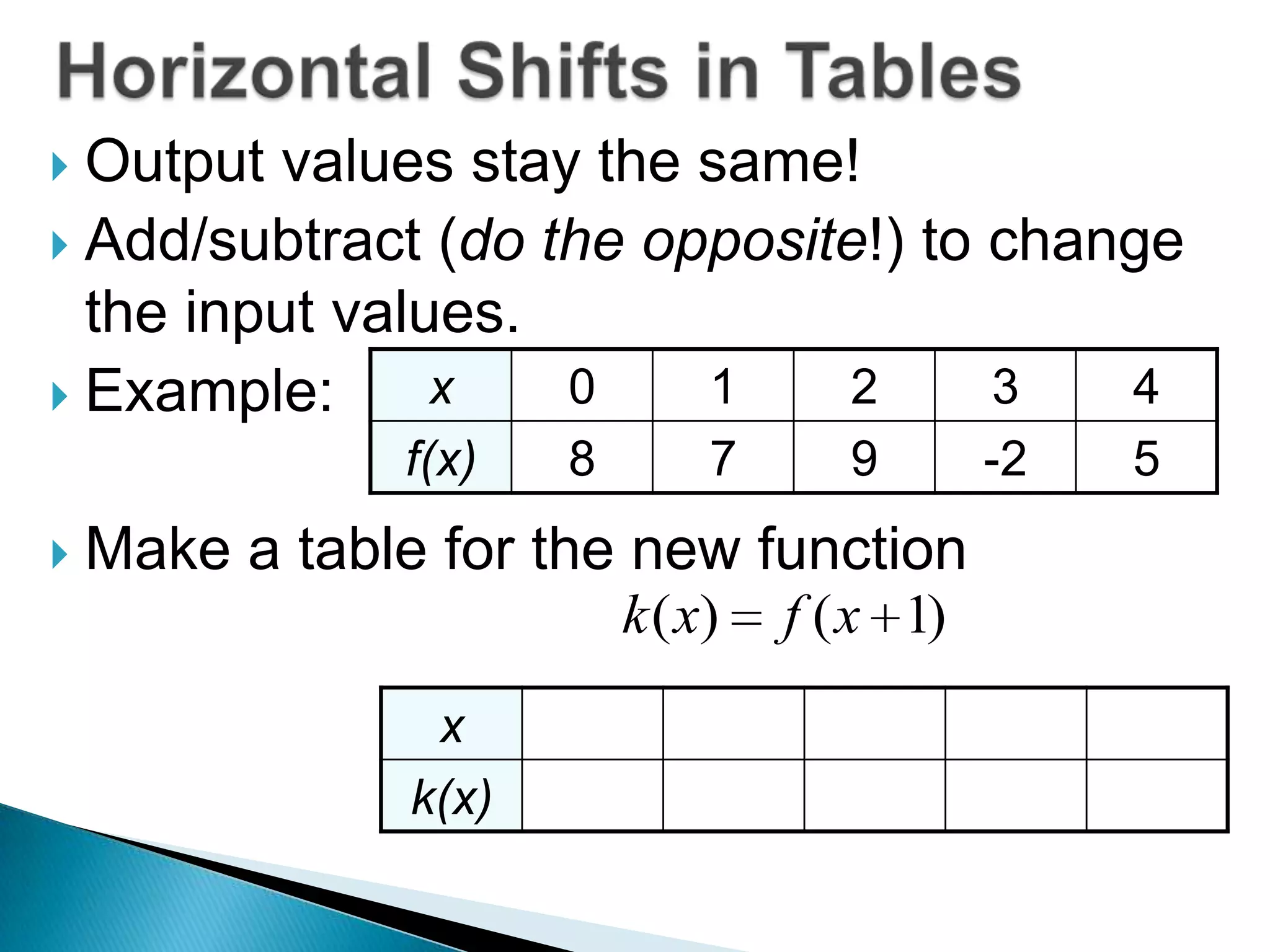
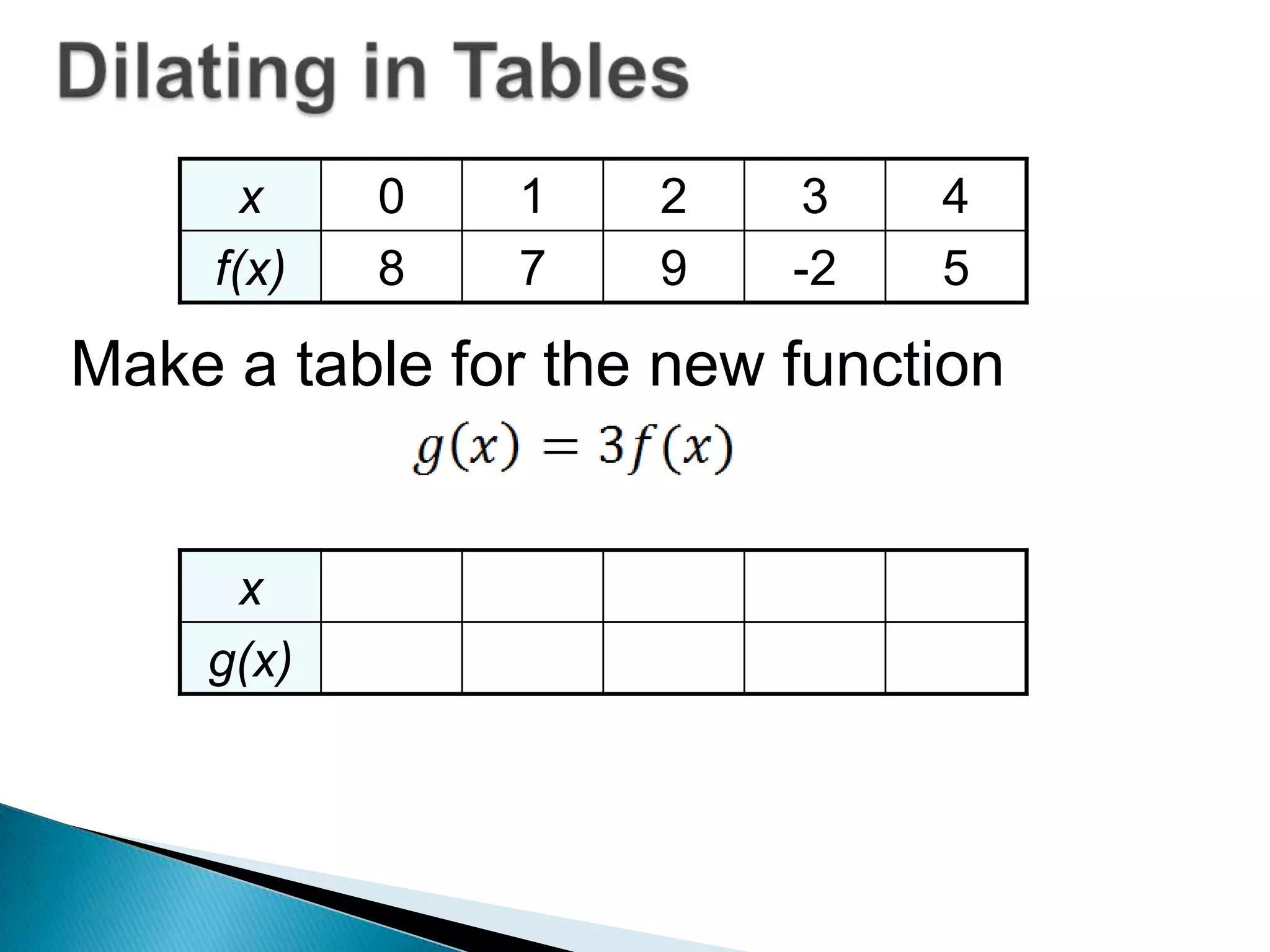
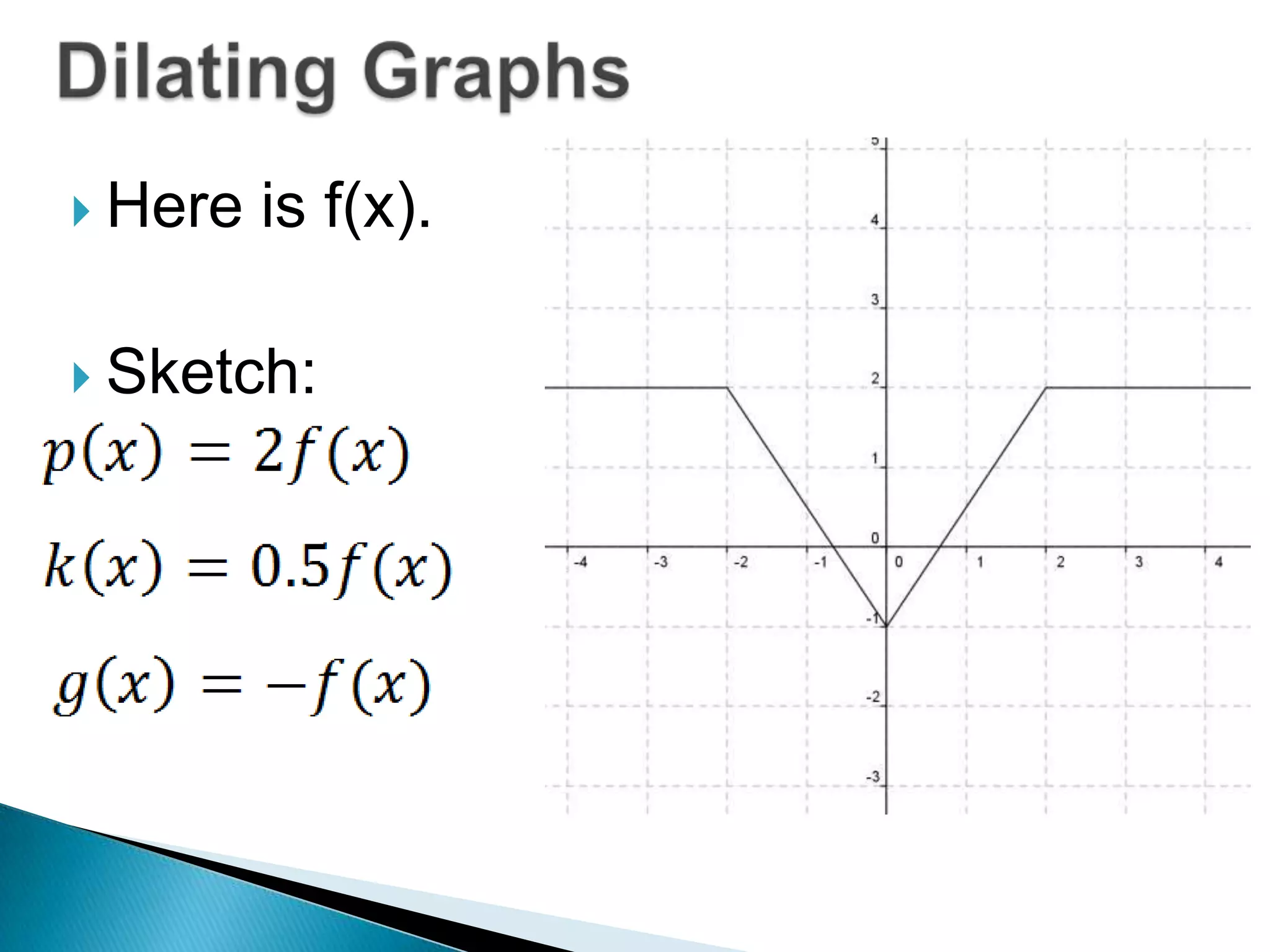
- The document discusses function transformations including translations, dilations, rotations, and reflections. It focuses on translations, which shift the graph up/down or left/right, and dilations, which shrink or stretch the graph. - Examples show how to write functions for translations like k(x)=f(x)+3 which shifts the graph up 3 units, and dilations like h(x)=2f(x) which stretches the graph vertically by a factor of 2. 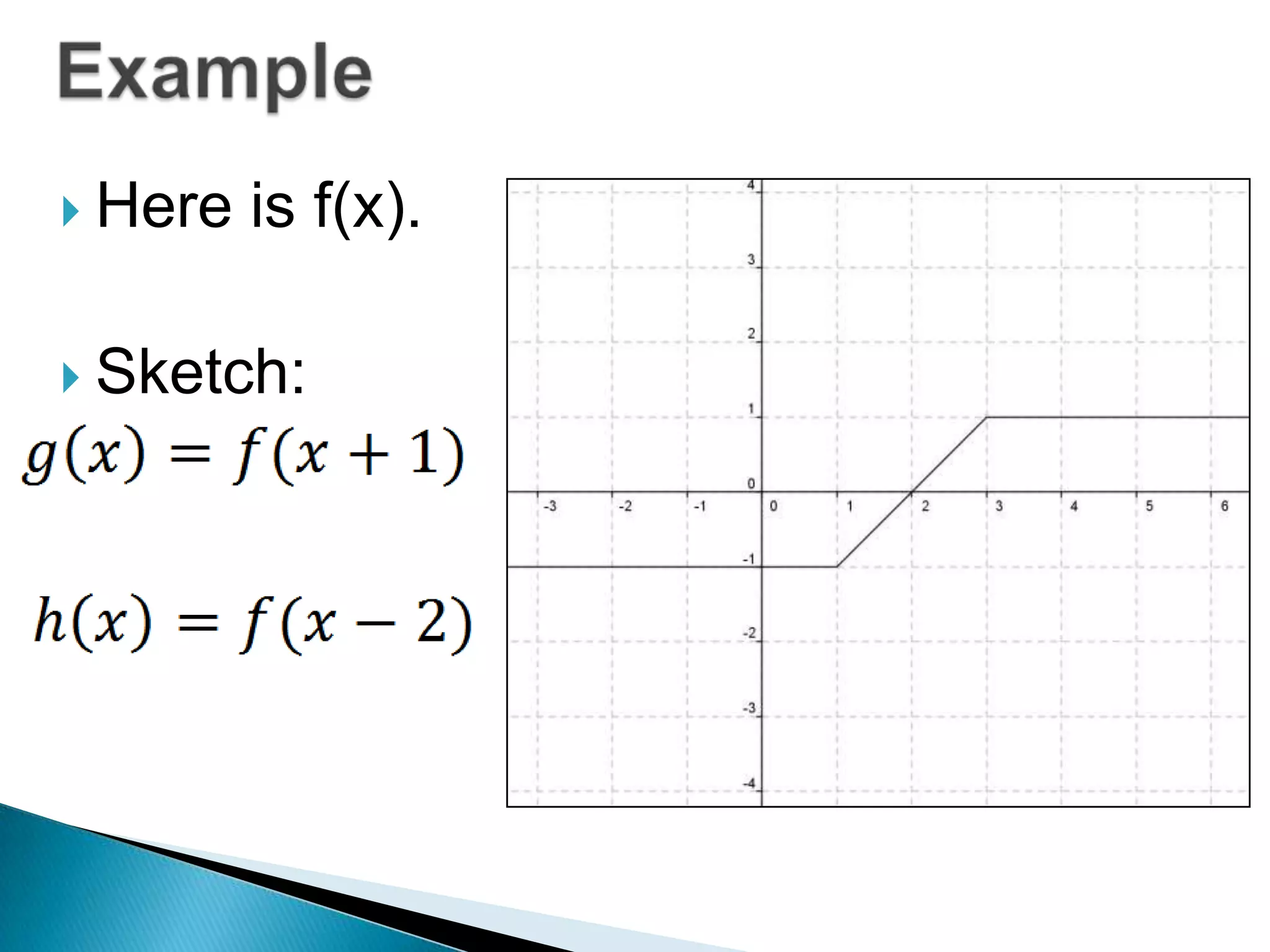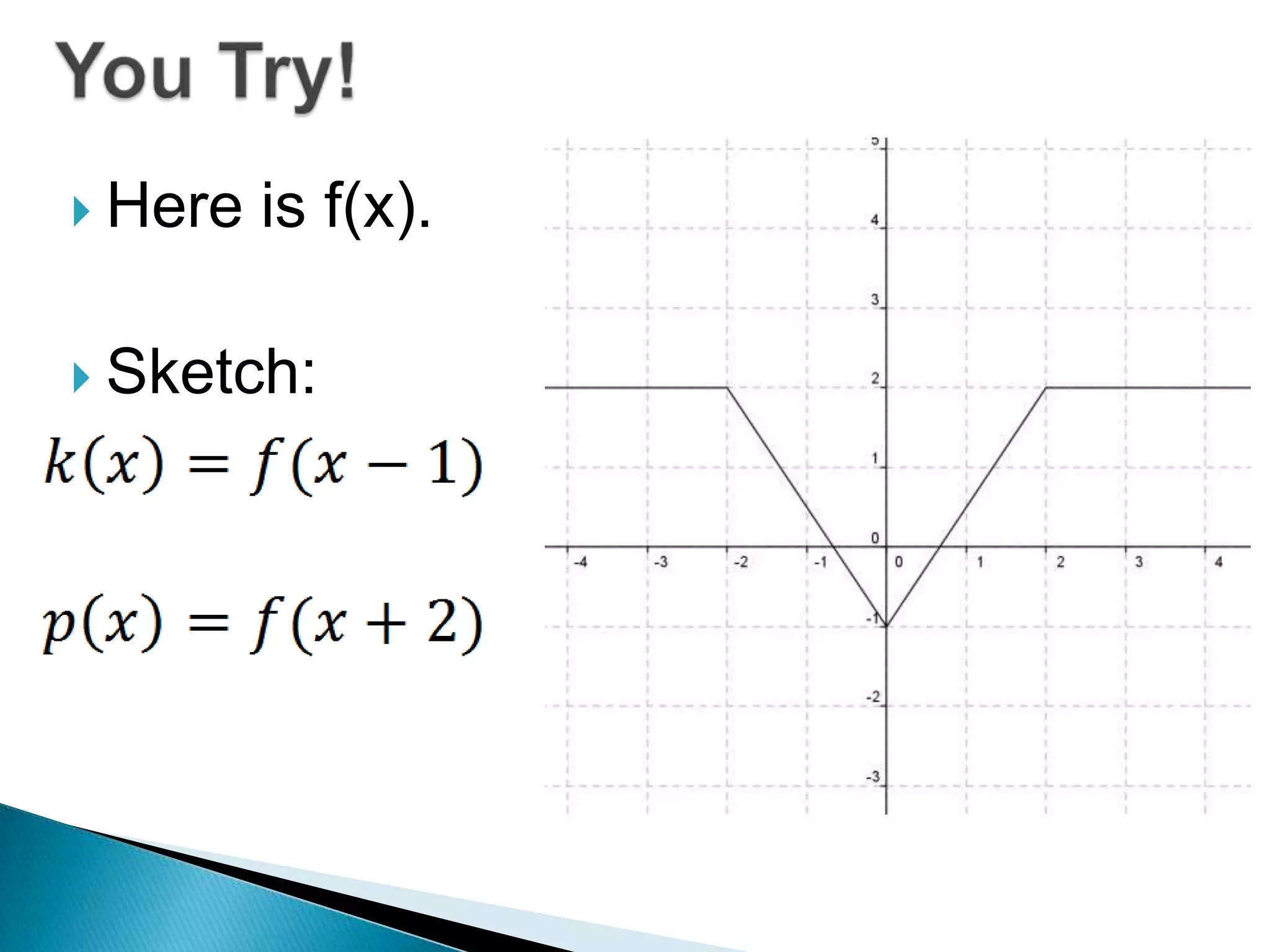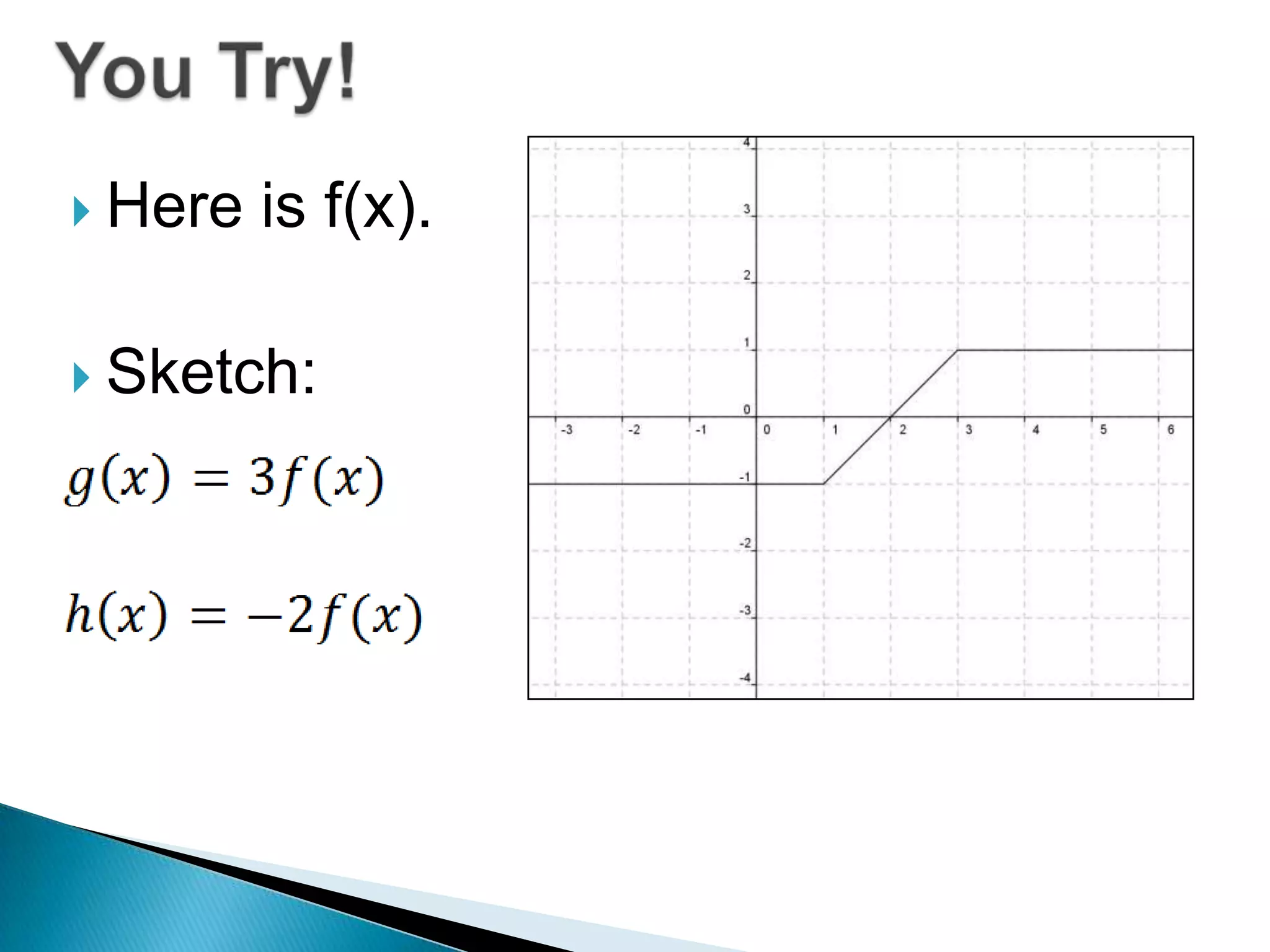- Questions provide the definition of a function f(x) and ask the reader to write the tables or sketch the graphs for new functions using transformations of f(x).

2. • When we make a new function based on an
old one, we call it a function
transformation
• Come in four basic categories:
• Translations (shifting/sliding)
• Dilations (shrinking or stretching)
• Rotations
• Reflections
• For now, we will study only
translations and dilations.

3.  We
can use function notation to build
new functions:
f ( x) 3
 Example 1: k ( x)
 The outputs for k are the same as for f
except we add 3 to them
2: k ( x) 2 f ( x)
 The outputs for k are 2 times the
outputs for f
 Example

4. 
Here’s the definition of f(x):
x
f(x)
0
8
1
7
2
9
3
-2
4
5
I want to make a new function k ( x)
 What does the table look like?

x
k(x)
0
11
1
10
2
12
3
1
4
8
f ( x) 3

5.  Use
this function definition to complete
the definitions below:
x
f(x)
0
8
1
7
2
9
3
-2
4
5
x
f(x)-7
0
1
2
3
4
x
f(x)+10
0
1
2
3
4

6.  Use
this function definition to complete
the definition below:
x
g(x)
x
g(x) – 3
0
12
1
9
2
-4
0
1
2
3
0
3
4
-1
4

7.  Here’s
the
definition of f(x):
I
want to make a
new function
k ( x) f ( x) 2
 What does the
graph look like?

8.  Here’s
the definition
of f(x):
I
want to make a
new function
k ( x)
f ( x) 1

9.  Use
the same
definition of f(x)
from the example:
 Draw
a graph for
the new function

10.  Vertical
shifts added/subtracted
something to the output values.
 Horizontal shifts will add/subtract
something to the input values.
Example: h(x) = f(x + 1)
is a horizontal shift.

11.  When
the input is changed, we need
to “undo” that change to see what
happens to the graph/table.
 So,
f(x + 1) means we subtract 1
from the x values.
 And, f(x – 1) means we add 1 to the x
values.

12. Output values stay the same!
 Add/subtract (do the opposite!) to change
the input values.
x
0
1
2
3
4
 Example:

f(x)

8
7
9
Make a table for the new function
k ( x)
x
k(x)
f ( x 1)
-2
5

13. x
f(x)
 Make
0
8
1
7
2
9
3
-2
4
5
a table for the new function
x
g(x)

14.  Remember
we “undo” the change to
the input, so:
 (x - #) means add  shift right
 (x + #) means subtract  shift left

15.  Here
is f(x).
 Sketch:

16.  Here
is f(x).
 Sketch:

17.  Dilations
occur when a function is
multiplied by a number.
 Vertical dilations – outputs multiplied
◦ 2f(x)
 Horizontal
dilations – inputs multiplied
◦ f(2x)
(We will only do vertical stretches/shrinks.)

18. x
f(x)
0
8
1
7
2
9
3
-2
4
5
Make a table for the new function
x
g(x)

19. x
f(x)
 Make
0
8
1
7
2
9
3
-2
4
5
a table for the new function
x
h(x)

20.  Here
is f(x).
 Sketch:

21.  Here
is f(x).
 Sketch: