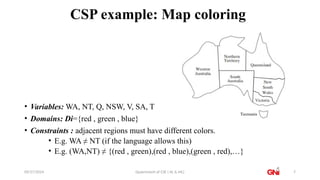
The document outlines a course on Artificial Intelligence, focusing on Constraint Satisfaction Problems (CSPs) and their applications, particularly in fields like scheduling and assignment. It defines CSPs, explains their structure, and discusses algorithms related to them, including backtracking and local search techniques. Key topics also include different variable types, constraints, and examples, such as map coloring.

1. 09/27/2024 Department of CSE (AI/ML) 1
22PCOAM11
INTROUCTION TO ARTIFICAL INTELLIGENCE
(R22 – II (Sem 3)
Department of computer science and engineering (AIML)
Session 10
by
Asst.Prof.M.Gokilavani
GNITC

2. 09/27/2024 Department of CSE (AI & ML)
TEXTBOOK:
• Artificial Intelligence A modern Approach, Third Edition, Stuart
Russell and Peter Norvig, Pearson Education.
REFERENCES:
• Artificial Intelligence, 3rd
Edn, E. Rich and K.Knight (TMH).
• Artificial Intelligence, 3rd
Edn, Patrick Henny Winston, Pearson
Education.
• Artificial Intelligence, Shivani Goel, Pearson Education.
• Artificial Intelligence and Expert Systems- Patterson, Pearson
Education.
2

3. Topics covered in Unit 2
09/27/2024 Department of CSE (AI/ML) 3
• Games: Optimal Decisions in Games
• Alpha–Beta Pruning
• Constraint Satisfaction Problems: Defining Constraint Satisfaction
Problems
• Constraint Propagation
• Backtracking Search for CSPs
• Knowledge-Based Agents
• Propositional Logic
• Propositional Theorem Proving: Inference and proofs
• Proof by resolution
• Horn clauses and definite clauses.

4. 09/27/2024 Dpaertment of CSE ( AL & ML) 4
Constraint Satisfaction Problems
• What is a CSP?
• Backtracking for CSP
• Local search for CSPs
• Problem structure and decomposition

5. 09/27/2024 Dpaertment of CSE ( AL & ML) 5
What is CSP?
• A constraint satisfaction problem (or CSP) is a special kind of
problem that satisfies some additional structural properties beyond the
basic requirements for problems in general.
Definition:
• State is defined by variables Xi with values from domain Di
• Goal test is a set of constraints specifying allowable
combinations of values for subsets of variables
• Solution is a complete, consistent assignment

6. 09/27/2024 Dpaertment of CSE ( AL & ML) 6
What is a CSP?
• In a CSP, the states are defined as,
• Finite set of variables V1, V2, …, Vn.
• Finite set of constrainsC1, C2, …, Cm.
• Non-emtpy domain of possible values for each variable DV1, DV2, …
DVn.
• Each constraint Ci limits the values that variables can take, e.g., V1 ≠ V2

7. 09/27/2024 Dpaertment of CSE ( AL & ML) 7
CSP example: Map coloring
• Variables: WA, NT, Q, NSW, V, SA, T
• Domains: Di={red , green , blue}
• Constraints : adjacent regions must have different colors.
• E.g. WA ≠ NT (if the language allows this)
• E.g. (WA,NT) ≠ {(red , green),(red , blue),(green , red),…}

8. 09/27/2024 Dpaertment of CSE ( AL & ML) 8
• A state is defined as an assignment of values to some or all variables.
• Consistent assignment: assignment does not violate the constraints.
• A solution to a CSP is a complete assignment that satisfies all constraints.
• Solution:
{WA=red,NT=green,Q=red,NSW=green,V=red,SA=blue,T=green}

9. 09/27/2024 Dpaertment of CSE ( AL & ML) 9
Constraint Satisfaction Problems
• Simple example of a formal representation language
• CSP benefits
• Standard representation language
• Generic goal and successor functions
• Useful general-purpose algorithms with more power than
standard search algorithms, including generic heuristics.
• Applications:
• Time table problems (exam/teaching schedules)
• Assignment problems (who teaches what)

10. 09/27/2024 Dpaertment of CSE ( AL & ML) 10
Varieties of CSPs
• Discrete variables
• Finite domains of size d O(dn) complete assignments.
⇒
• Eg: a Boolean CSP, NP-Complete problem
• Infinite domains (integers, strings, etc.)
• Eg: job scheduling, variables are start/end days for each job
• Need a constraint language
• Eg: StartJob1 +5 ≤ StartJob3.
• Linear constraints solvable, nonlinear undecidable.
• Continuous variables
• Linear constraints solvable in poly time by linear programming
methods (deal with in the field of operations research).
• Our focus: discrete variables and finite domains

11. 09/27/2024 Dpaertment of CSE ( AL & ML) 11
Varieties of Constrains
• Unary constraints involve a single variable.
• e.g. SA ≠ green
• Binary constraints involve pairs of variables.
• e.g. SA ≠ WA
• Global constraints involve an arbitrary number of variables.
Eg: Crypth-arithmetic column constraints.
• Preference (soft constraints) e.g. red is better than green often
representable by a cost for each variable assignment; not considered
here.

12. 09/27/2024 Dpaertment of CSE ( AL & ML) 12
Real-world CSP’s
• Assignment problems
• e.g., who teaches what class
• Timetable problems
• e.g., which class is offered when and where?
• Transportation scheduling
• Factory scheduling

13. 09/27/2024 Dpaertment of CSE ( AL & ML) 13
CSP as a standard search problem
Incremental formulation
• States: Variables and values assigned so far
• Initial state: The empty assignment
• Action: Choose any unassigned variable and assign to it a value that does not
violate any constraints
• Fail if no legal assignments
• Goal test: The current assignment is complete and satisfies all constraints.
• Same formulation for all CSPs !!!
• Solution is found at depth n (n variables).
• What search method would you choose?
• How can we reduce the branching factor?

14. 09/27/2024 Dpaertment of CSE ( AL & ML) 14
Commutative
• CSPs are commutative.
• The order of any given set of actions has no effect on the outcome.
• Example: choose colors for Australian territories one at a time
• [WA=red then NT=green] same as [NT=green then WA=red]
• All CSP search algorithms consider a single variable assignment
at a time there are d
⇒ n leaves.

15. 09/27/2024 Dpaertment of CSE ( AL & ML) 15
Topics to be covered in next session
11
• Backtracking Search for CSPs
Thank you!!!