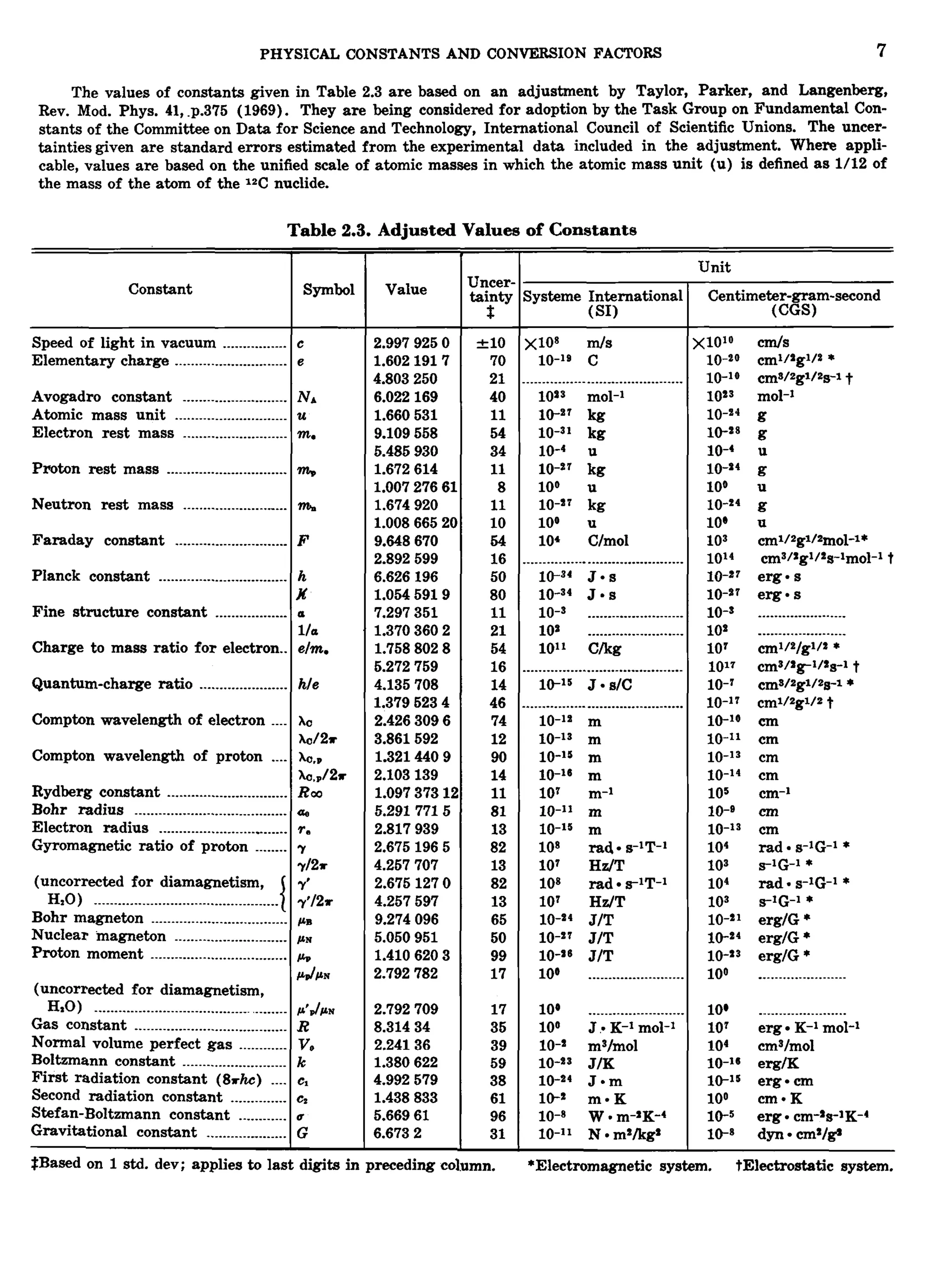
This document contains tables of physical constants, conversion factors, and other reference information. Table 2.1 lists common units in the SI and CGS systems and conversion factors between them. Table 2.2 provides names and conversion factors for electric and magnetic units in SI, emu, and esu systems. Table 2.3 gives adjusted values of fundamental physical constants with uncertainties. Tables 2.4-2.6 provide additional conversion factors, constants, and geodetic information.

1. 2. Phvsical Constants and Conversion FactorsJ
Table 2.1.
Table 2.2.
Table 2.3.
Table 2.4.
Table 2.5.
Table 2.6.
A. G. MCNISH
Contents
page
6Common Units and Conversion Factors . . . . . . . . .
Names and Conversion Factors for Electric and Magnetic
u n i t s . . . . . . . . . . . . . . . . . . . . . . . 6
7Adjusted Values of Constants . . . . . . . . . . . . .
8Miscellaneous Conversion Factors. . . . . . . . . . . .
Conversion Factors for Customary U.S.Units to Metric
u n i t s . . . . . . . . . . . . . . . . . . . . . . . 8
. . . . . . . . . . . . . . . . . . 8Geodetic Constants
1 National Bureau of Standards.
6

2. 2. Physical Constants and Conversion Factors
esu
name
The tables in this chapter supply some of the
more commonly needed physical constants and
conversion factors.*
The International System of Units (SI)
established in 1960 by the General Conference
of Weights and Measures under the Treaty of
the Meter is based upon: the meter (m) for
length, defined as 1 650 763.73 wave-lengths
in vacuum corresponding to the transition
*2p,,-5d5 of krypton 86; the kilogram (kg)
for mass, defined as the mass of the prototype
kilogram at Sevres, France; the second (s) for
time, defined as the duration of 9 192 631 770
periods of the radiation corresponding to the
transition between the two hyperfine levels of
cesium 133; the kelvin (K) for temperature,
defined as 1/273.16 of the thermodynamic tem-
perature of the triple point of water; the am-
pere (A) for electric current, defined as the
current which, if flowing in two infinitely long
parallel wires in vacuo separated by one meter,
would produce a force of 2 x lo-’newtons per
meter of length between the wires; and the
candela (cd) for luminous intensity, defined as
the luminous intensity of 1/600 000 square
meter of a perfect radiator at the temperature
of freezing platinum.
All other units of SI are derived from these
base units by assigning the value unity to the
proportionality constants in the defining equa-
tions (official symbols for other SI units appear
in Tables 2.1 and 2.2). Taking 1/100 of the
*Seealso “Prefaceto Ninth Printing," pageIIIa and page11.
emu-SI esu-SI
factors factors
meter as the unit for length and 1/1000 of the
kilogram as the unit for mass gives rise simi-
larly to the cgs system, often used in physics
and chemistry.
SI, as it is ordinarily used in electromagne-
tism, is a rationalized system, Le., the electro-
magnetic units of SI relate to the quantities
appearing in the so-called rationalized electro-
magnetic equations. Thus, the force per unit
length between two current-carrying parallel
wires of infinite length separated by unit dis-
tance in vc1cuo is 2f = pLoili2/4n,where-k,has
the value 4~ x 10-’H/m. The force between
two electric charges in vacuo is corresponding-
ly given by f = qlq,/4n~,,r2,e,, having the value
l/p,,c2,where c is the speed of light in meters
per second. (~,,-8.854 y 10-*2F/m)
Setting p,, equal to unity and deleting 4~
from the denominator in the first equation
above defines the cgs-emu system. Setting
equal to unity and deleting 4~ from the de-
nominator in the second equation correspond-
ingly defines the cgs-esu system. The cgs-emu
and the cgs-esu systems are most frequently
used in the unrationalized forms.
Table 2.1. Common Units and Conversion
Factors, CGS System and SI
I SI I CGS I_ . ~
Quantity I Name I Name I Factor
Force I newton (N)I dvne I 105
Energy joule (Jj erg 107
Power I watt (w). I ........................ I 10’
Table 2.2. Names and Conversion Factors for Electric and Magnetic Units
Quantity
Current
Charge
Potential
Resistance
lnductance
Capacitance
Magnetizing force
Magnetomotive force
Magnetic flux
Magnetic flux density
Electric displacement
SI
name
ampere (A)
coulomb (C)
volt (V)
ohm (0)
henry (H)
farad (F)
A m-1
A
weber (Wb)
tesla ( T )
......................
emu
name
abampere
abcoulomb
abvolt
abohm
centimeter
oersted
gilbert
maxwell
gauss (G)
........................
statampere
statcoulomb
statvolt
statohm
centimeter
........................
........................
10-1
10-1
108
109
109
10-9
4r x 10-3
4r x 10-1
108
10‘
10-5
-3 x 109
-3 x 109
-(1/9)X 10-11
-(1/9)x lo-”
-9 x 10”
-3 x 109
-3/106
-(1/3)x lo-*
-(1/3) x
-(1/3)x 10-2
-3 x 105
Example: If the value assigned to a current is 100 amperes its value in abamperes is 100 x lo-’=10.
6

3. PHYSICAL CONSTANTS AND CONVERSION FACTORS 7
I I
The values of constants given in Table 2.3 are based on an adjustment by Taylor, Parker, and Langenberg,
Rev. Mod. Phys. 41,.p.375 (1969). They are being considered for adoption by the Task Group on Fundamental Con-
stants of the Committeeon Data for Science and Technology, International Council of Scientific Unions. The uncer-
taintiesgiven are standard errors estimated from the experimental data included in the adjustment. Where appli-
cable, values are based on the unified scale of atomic masses in which the atomic mass unit (u) is defined as 1/12 of
the mass of the atom of the 12C nuclide.
Table 2.3. Adjusted Values of Constants
Constant
Speed of light in vacuum _________~ _____.
Elementary charge ............................
Avogadro constant ..........................
Atomic mass unit ............................
Electron rest mass ..........................
Proton rest mass ..............................
Neutron rest mass ..........................
Faraday constant ............................
Planck constant ................................
Fine structure constant __________________
Charge to mass ratio for electron..
Quantum-charge ratio .._._____~ ___________.
Compton wavelength of electron ....
Compton wavelength of proton .___
Rydberg constant ..............................
Bohr radius ......................................
Electron radius ................................
Gyromagnetic ratio of proton ........
(uncorrected for diamagnetism,
HzO) ..............................................
Bohr magneton ..................................
Nuclear magneton _.____..___________.._______
Proton moment ..................................
I
(uncorrected for diamagnetism,
Gas constant ......................................
Normal volume perfect gas ............
Boltzmann constant ..........................
First radiation constant (8rhc) _.._
Second radiation constant ..............
Stefan-Boltmann constant ............
Gravitational constant .....
HzO) ...............................................
Symbol
C
e
NA
U
m.
nz,
nk
F
h
X
a
l/a
elm.
hle
ha
b/2+
xC.P
b . p / Z r
RCO
Q
Ta
Y
Y12*
Y'
-f*12r
PS
P N
IC,
CJPN
P'JPN
R
VO
k
Cl
C2
U
G
2.997 925 0
1.602 1917
4.803 250
6.022 169
1.660 531
9.109 558
5.485 930
1.672 614
1.007 276 61
1.674 920
1.008 665 20
9.648 670
2.892 599
6.626 196
1.054 5919
7.297 351
1.370 360 2
1.758802 8
5.272 759
4.135 708
1.379 523 4
2.426 309 6
3.861 592
1.321 440 9
2.103 139
1.097 373 12
5.291 771 5
2.817 939
2.675 196 5
4.257 707
2.675 127 0
4.257 597
9.274 096
5.050951
1.410 620 3
2.792 782
2.792 709
8.314 34
2.241 36
1.380 622
4.992 579
1.438 833
5.669 61
6.673 2
f10
70
21
40
11
54
34
11
8
11
10
54
16
50
80
11
21
54
16
14
46
74
12
90
14
11
81
13
82
13
82
13
65
50
99
17
17
35
39
59
38
61
96
31
Systeme International
(SI)
<lo8 m/s
10-19 c
1013 mol-'
10-31 kg
lO-*7 kg
100 u
lo-*? kg
100 u
104 C/mol
1047 kg
10-4 u
.......................................
l e 3 4 J - s
10-34 J * s
10-3 ........................
10' ........................
10" Ckg
i o - 1 5 J . ~ / c
.......................................
10-1'
10-13
10-15
107
10-15
107
107
1044
10-27
10-16
10-11
108
108
10-'6
100
m
m
m
m
m-1
m
m
rad s-lT-1
HdT
rad ~ 1 T - l
HdT
JIT
JIT
JIT
100 ........................
loo J :K-1 mol-*
lo-* mVmol
10-24 J - m
10-* m * K
10-11 N m*/kgs
1 0 4 3 JIK
10-8 w.m - 2 ~ - 4
10' ......................
107 erg K-1 mol-'
104 cm3lmol
10-16 erglK
10-15 erg cm
100 c m *K
10-5 erg cm-2s-IK-4
10-8 dm ~m*l@
$Based on 1 std. dev; applies to last digits in preceding column. *Electromagnetic system. tElectrostatic system.

4. 8 PHYSICAL CONSTANTS AND CONVERSION FACTORS
Table 2.4. Miscellaneous Conversion Factors
Standard gravity, go = 9.806 65 meters per second per second*
Standard atmospheric pressure, Po = 1.01325 X lo5newtons per square meter*
= 1.01325 x lo6 dynes per square centimeter*
1 thermodynamic calorie,' cal, =4.1840 joules*
1 IT calorie2,cal, = 4.1868 joules*
1 liter, 1 = cubic meter*
1 angstrom unit, A = 10-lometer*
1 bar = lo5 newtons per square meter*
= lo6 dynes per square centimeter*
1 gal = meter per second per second*
= 1 centimeter per second per second*
1 astronomical unit, AU = 1.496 x 10" meters
1 light year = 9.46 X 1015meters
1 parsec = 3.08 x 10l6meters
= 3.26 light years
1 curie, the quantity of radioactive material undergoing 3.7 x 1Olo disintegrations per second*.
1 roentgen, the exposure of x- or gamma radiation which'produces together with its secondaries
2.082 x loDelectron-ion pairs in 0.001 293 gram of air.
The index of refraction of the atmosphere for radio waves of frequency less than,3 X 1O1OHz
is given by (n- 1)lo6= (77.6/t) (p + 4810e/t), where n is the refractive index; t, temperature
in kelvins; p, total pressure in millibars; e, water vapor partial pressure in millibars.
Factors for converting the customary United
States units to units of the metric system are
given in Table 2.5.
Table2.5. Factore for ConvertingCustomary
U.S. Units to SI Units
1 yard 0.914 4 meter*
1 foot 0.304 8 meter*
1 inch 0.0254 meter*
1 statutemile 1609.344 meters*
1 nautical mile (inter- 1852 meters*
national)
1 pound (avdp.) 0.45359237 kilogram*
1 oz. (avdp.) 0.028349 52 kilogram
1 pound force 4.448 22 newtons
1 slug 14.5939 kilograms
1 poundal 0.138 255 newtons
1 foot pound
Temperature 32 + (9/5) Celsius
(Fahrenheit) temperature*
1 British thermal unitS 1055 joules
1.355 82 joules
1 Used principally by chemists.
* Used principally by engineers.
Geodetic constants for the international
(Hayford) spheroid are given in Table 2.6.
The gravity values are on the basis of the re-
vised Potsdam value. They are about 14 parts
per million smaller than previous values. They
are calculated for the surface of the geoid by
the international formula.
Table 2.6. Geodetic Constants
a = 6 378 388 m; f = 1/297; b = 6 356 912 m
Latitude
00
15
30
45
60
75
90
Length of
1' of
longitude
Meters
1855.398
1792.580
1608.174
1314.175
930.047
481.725
0
Length of
1' of
latitude
Meters
1842.925
1844.170
1847.580
1852.256
1856.951
1860.401
1861.666
nt/SS
9.780350
9.783 800
9.793238
9.806 154
9.819 099
9.828 593
9.832 072
9 Various definitions are given for the British thermal unit. This represents a rounded mean value differing
from none of the more important definitions by more than 3 in 104.
* Exact value.