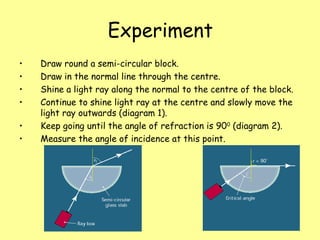
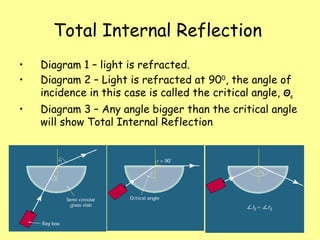
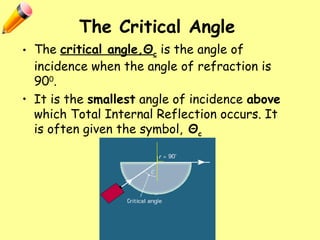
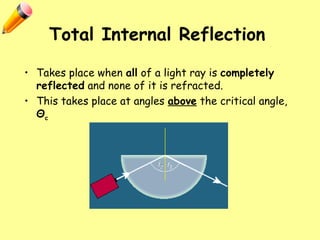
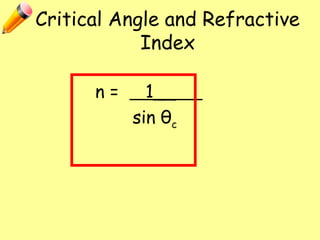
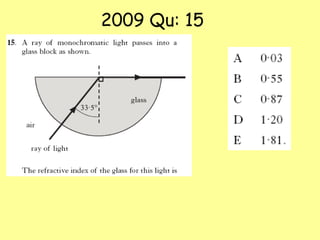
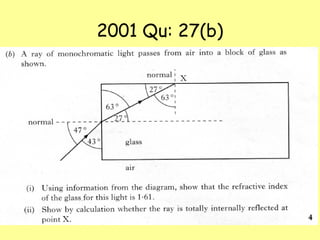
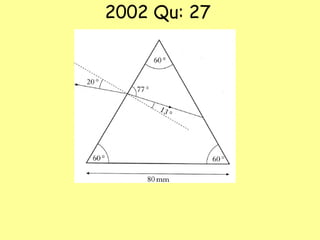
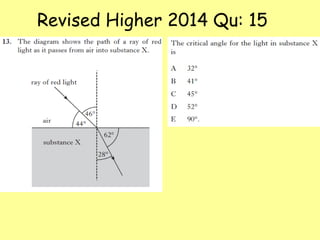
The document explains total internal reflection and the critical angle, emphasizing their relationship with refractive index and the conditions for total internal reflection to occur. It outlines an experimental procedure to find the critical angle, including diagrams and calculations. Furthermore, it highlights applications of total internal reflection in telecommunications, such as in optical fibers.

1. Key areas
• Critical angle and total internal
reflection.

2. What we will do today:
• State what is meant by Total Internal
Reflection and the Critical Angle.
• State the relationship between the
refractive index and the critical angle.
• Carry out calculations on the above.

3. Total Internal Reflection and
Critical Angle

4. Revision from last day
• sin θ1 / sin θ2 = λ1 / λ2 = v1 / v2
• n = sin θ1 / sin θ2
• We can express this as:
n2 / n1 = sin θ1 / sin θ2
NB The refractive index of air is 1.

5. Experiment
• Draw round a semi-circular block.
• Draw in the normal line through the centre.
• Shine a light ray along the normal to the centre of the block.
• Continue to shine light ray at the centre and slowly move the
light ray outwards (diagram 1).
• Keep going until the angle of refraction is 900
(diagram 2).
• Measure the angle of incidence at this point.

6. Total Internal Reflection
• Diagram 1 – light is refracted.
• Diagram 2 – Light is refracted at 900
, the angle of
incidence in this case is called the critical angle, Θc
• Diagram 3 – Any angle bigger than the critical angle
will show Total Internal Reflection

7. The Critical Angle
• The critical angle,Θc is the angle of
incidence when the angle of refraction is
900
.
• It is the smallest angle of incidence above
which Total Internal Reflection occurs. It
is often given the symbol, Θc

8. Total Internal Reflection
• Takes place when all of a light ray is completely
reflected and none of it is refracted.
• This takes place at angles above the critical angle,
Θc

9. Curved Surface
• Note that there is no refraction at the
curved surface because a radial ray
strikes the surface at normal incidence
(i.e. perpendicular - 90º).
• This is why a semi-circular block is
used to find the critical angle.

10. Uses of Total Internal Reflection
• Total internal reflection is used to send
light signals along optical fibres.
• This can be used to send
telecommunications such as internet, TV
and phone.
• This is how Virgin Media provide their
services.

11. Critical Angle and Refractive
Index
n = 1__
sin θc

12. Example
• n = 1.4
• Θc = ?
• n = 1
sin Θc
1.4 = 1
sin Θc
sin Θc = 1
1.4
Θc = (sin-1
) 1
1.4
Θc = 45.6o

13. 2008 Qu: 16

14. 2009 Qu: 15

15. 2001 Qu: 27(b)

16. 2002 Qu: 27

17. 2002 Qu: 27

18. Revised Higher 2014 Qu: 15

19. Revised Higher
Past Paper Questions
• 2012 Qu: 29
• 2013 Qu: 29