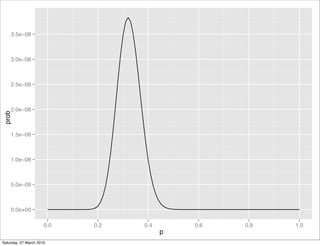
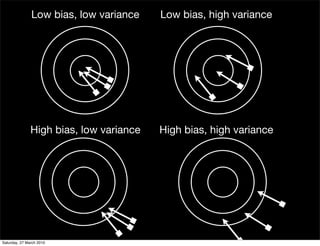
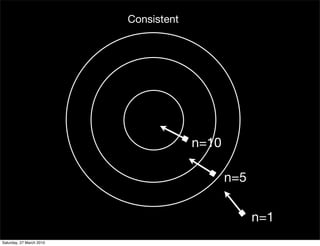
This document contains notes from a statistics course on introduction to inference. It discusses key topics like continuity correction, estimators and their properties, the difference between data and distributions, the plug-in principle of using sample statistics to estimate population parameters, and important properties of estimators like being unbiased, having low variance, and being consistent. It also includes examples of estimating the proportion of people who smoke marijuana from survey data.