Документ представляет учебник математики для 4 класса, часть 2, разработанный в соответствии с федеральными образовательными стандартами. Он охватывает алгоритмы действий с величинами, деление столбиком и решение задач с пропорциональными величинами. Включает упражнения для повторения и закрепления изученного материала, а также вопросы для самоконтроля.



![УДК 51(075.2)
ББК 22.1я71
4-37
Чекин А.Л.
4-37 Математика [Текст] : 4 кл. : Учебник : В 2 ч./А.Л. Чекин; под
ред. Р. Г. Чураковой. — 2-е изд. — М.: Академкнига/
Учебник, 2012. — Ч. 2 : 128 с. : ил.
13ВЫ 978-5-49400-089-7 (общ.)
15ВЫ 978-5-49400-091-0 (ч. 2)
Учебник в двух частях разработан в соответствии с требовани
ями федерального государственного образовательного стандарта
начального общего образования и концепцией комплекта
«Перспективная начальная школа». Каждая из частей рассчитана
на учебное полугодие.
Учебник рекомендуется использовать в комплекте с тетрадями
для самостоятельной работы №1, №2 и №3. Во вторую часть
включены вопросы, связанные с изучением алгоритма деления
столбиком, действий над величинами, обучением решению задач
с пропорциональными величинами, применением уравнений для
решения сюжетных арифметических задач.
Большое внимание уделяется работе с данными, а также
вопросам повторения основных тем всего курса.
УДК 51 (075.2)
ББК 22.1я71
Учебное издание
Чекин Александр Леонидович
МАТЕМАТИКА
4 класс
Учебник
В двух частях
Часть 2
Подписано в печать 26.06.2012. Формат 70x90/16.
Гарнитура Ргадтайса С. Печать офсетная. Бумага офсетная.
Печ. л. 8,0. Доп. тираж 10000 экз. Тип. зак. № 33048.
Издател ьство «Академкнига/Учебн ик»
117997 Москва, ул. Профсоюзная, д. 90, офис 602
Тел.: (495) 334-76-21, факс (499) 234-63-58.
Е -та Н : а са б е ти сН @ та 1к.ги ллллл/.акас1етктда.ги
Отпечатано в соответствии с качеством предоставленных издательством
электронных носителей в ОАО «Саратовский полиграфкомбинат».
410004, г. Саратов, ул. Чернышевского, 59. лллллл5агрк.ги
Г,1Ш 978-5-49400-089-7 (общ.)
15ВЫ 978-5-49400-091-0 (ч. 2)
© Чекин А. Л., 2011
© Оформление, ООО «Издательств
«Академкнига/Учебник», 2012
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Работа в парах
Не торопись с ответом,
ш ь| подумай
Работа в группе
Выскажи предположение
Проверь правильность
выполнения задания
55. Трудное задание
Загляни в словарь* (с. 123)
ЗАПОМНИ СЛОВО
Правило
Смотри Тетрадь для самостоятель-
П ной работы № 2, страница 7](https://image.slidesharecdn.com/42-170811133557/85/2-4-320.jpg)














![Нахождение части от величины
97. «Маша, я правильно догадался, что для
нахождения двух третей от 60 кг можно сначала
найти одну треть от 60 кг, а потом эту долю удво
ить?» — спросил Миша у сестры.
«Ты прав. Так можно поступать и во всех других
подобных случаях. Например, для нахождения трёх
четвертей от этой величины сначала можно найти
одну четверть, а потом эту долю утроить», — под
твердила Маша.
Вычисли, чему равняются две трети от 60 кг и
три четверти от 60 кг.
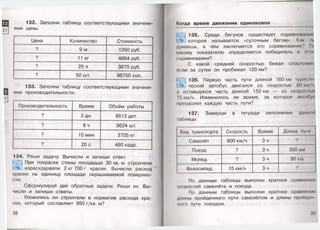
98. Рассмотри диаграмму слева и назови, какую
с л часть от площади всего круга составляет пло
щадь закрашенной части, если круг разделён на оди
наковые доли.
□ ученики-отличники
□ остальные ученики
С помощью круговой диаграммы справа выясни,
какую долю составляют отличники. Сколько отличников
в классе, если в классе 28 учеников?
99. Чему равны три седьмых некоторой длины,
если её одна седьмая часть равна 25 м?
100. Вычисли три седьмых от каждой из следу
ющих величин.
49 т 147 л 294 кв. м 301 куб. см
30
101. Реши задачу. Вычисли и запиши ответ
Туристам нужно преодолеть расстояние 40 км :(
день они смогли пройти три четверти этого пун
Сколько километров им осталось пройти?
При решении используй следующую схему.
__________ I_________ _]_______
40 км
102. Сформулируй задачу на нахождение дп
седьмых некоторой массы, если известно, что н< ••
масса равна 70 кг.
Запиши решение сформулированной задачи сна
чала по действиям, а потом в виде одного вырнжо
ния.
Вычисли и запиши ответ.
3|йН 103. Найди от массы 120 кг следующие часш
ш м две трети, три четверти, четыре пятых, чсмырн
шестых, пять восьмых.
Есть ли среди полученных результатов одинако
вые? Как это можно объяснить?
Докажи с помощью схемы, что три четвёртых и
шесть восьмых от одной и той же величины равны
104. Туристы каждый день проходили одно и
же расстояние. За неделю они прошли 175 км. За
сколько дней они пройдут три седьмых этого рассю
у ш и я ? Сколько километров туристы прошли за 3 дня?](https://image.slidesharecdn.com/42-170811133557/85/2-19-320.jpg)





![^Щ ] 147. Маша, проиграв соревнование в скорости
Э Й Мише, предложила соревноваться по-другому:
сначала она уедет вперёд на 200 м, а только потом
Миша начнёт её догонять. Сможет ли Миша догнать
Машу, если весь путь, как и раньше, составит 1 км,
а скорость передвижения у них будет той же самой:
250 м/мин и 200 м/мин соответственно?
148. Реши задачу. Вычисли и запиши ответ.
От одной автостанции по одному и тому же
маршруту с интервалом в 1 ч отправились сначала
автобус, затем легковое такси. Средняя скорость
автобуса — 60 км/ч, а такси — 80 км/ч. Через
сколько часов такси догонит автобус?
Установи сначала, какой путь пройдёт автобус за
1 ч. После этого найди, с какой скоростью будет
уменьшаться расстояние между автобусом и такси.
149. Когда спортсмен из команды 4 «А» класса
*> на последнем этапе принял эстафетную палочку
от своего товарища, его соперник из команды 4 «Б»
класса был впереди на 15 м. Участник из команды
4 «Б» бежит со скоростью 5 м/с, а его соперник —
6 м/с. Через сколько секунд второй догонит первого?
Сможет ли победить команда 4 «А», если длина
заключительного этапа составляет 90 м?
150. Используя следующее правило, вычисли
скорость изменения расстояния между каждой парой
автомобилей, движущихся в одном направлении, если
скорости этих автомобилей постоянны и равны соот
ветственно 80 км/ч, 20 м/с и 1000 м/мин.
44
I
При движении в одном направлении скорое п.
изменения расстояния между движущимися объок
тами равна разности скоростей этих объектов.
151. Реши задачу. Вычисли и запиши ответ.
От одной пристани одновременно вниз по гечо
иию реки отплыли катер и плот. На каком расстоянии
они окажутся друг от друга через 2 ч движения, если
скорость катера в стоячей воде 20 км/ч?
Нужно ли для ответа на требование задачи знай
скорость движения плота, которая совпадает со ем>
ростью течения реки?
Можно ли найти расстояние, пройденное катером
' “л за 2 ч движения вниз по течению реки, если ми
«наем только скорость катера в стоячей поди
Почему? Что для этого нужно ещё знать?
Вычисли это расстояние, если скорость течения
реки 2 км/ч.
152. Сформулируй задачу на движение в одном
и том же направлении, которое началось одновремон
по из одного пункта. Числовые данные для формули
ровки задачи можно взять из следующей схемы.
50 км/ч >
70 км/ч__________>
Реши сформулированную задачу. Вычисли и запи
ши ответ.](https://image.slidesharecdn.com/42-170811133557/85/2-26-320.jpg)







![191. Реши данную задачу двумя способами:
вычисляя и не вычисляя производительность.
За 3 ч работы с конвейера сошло 48 автомоби
лей. Сколько автомобилей сойдёт с конвейера за 12 ч
работы с той же производительностью?
Для каждого варианта решения вычисли и запи
ши ответ.
Сколько часов должен работать этот конвейер
с той же производительностью, чтобы выпустить
160 автомобилей?
Какой вариант решения данной задачи может
помочь найти ответ на это новое требование?
192. При совместной работе мастер и его уче
ник за 2 ч работы могут обработать 24 детали. За
какое время при сохранении той же производительно
сти сможет обработать эти 24 детали один ученик,
если производительность мастера в 3 раза выше, чем
производительность ученика?
Реши задачу. Вычисли и запиши ответ.
Для вычисления производительности ученика вос
пользуйся следующей схемой.
1 ч. Зч.
Какую величину изображает вся полоска? Как вы
числить значение этой величины?
Какую величину изображает одна часть данной
полоски? Как вычислить значение этой величины?
60
193. При совместной работе мастер и его учо
ник за 2 ч работы могут обработать 24 детали. 3.1
какое время при сохранении той же производительно
сти сможет обработать эти 24 детали один ученик,
если производительность мастера на 6 дет./ч выше,
чем производительность ученика?
Реши задачу. Вычисли и запиши ответ.
Для вычисления производительности ученика вое
пользуйся следующей схемой.
6 дет./ч
Т®] Какую величину изображает вся полоска? Чему
равно значение этой величины?
194. Реши задачу. Вычисли и запиши ответ.
В первый день туристы были в пути 10 ч, а но
второй 7 ч. За второй день пути туристы преодолели
расстояние на 12 км меньше, чем за первый.
Сколько километров туристы прошли за эти дни
дня, если за каждый час движения они преодолевали
одинаковое расстояние?
195. Вычисли значения данных выражений.
а) (25241 + 37889) • 12: (69581 - 69577)
б) (35472 + 27792): 12 • (78953 - 78929)
61](https://image.slidesharecdn.com/42-170811133557/85/2-34-320.jpg)
![Когда количество одинаковое
196. Реши каждую из данных задач.
а. Автобус первые четыре часа ехал со скоро
стью 40 км/ч, а следующие четыре часа со скоростью
в 2 раза больше. Во сколько раз больше путь проде
лал автобус за вторые четыре часа по сравнению
с первыми?
б. Токарь первые четыре часа работал с произ
водительностью 40 дет./ч, а следующие четыре часа
с производительностью в 2 раза больше. Во сколько
раз больше деталей обработал токарь за вторую
половину 8-часового рабочего дня, чем за первую?
в. Покупатель сначала купил 4 кг смородины по
цене 40 руб./кг, а потом 4 кг абрикосов по цене
в 2 раза больше. Во сколько раз больше заплатил
покупатель за вторую покупку, чем за первую?
Чем эти задачи похожи и чем они отличаются?
Можно ли с помощью одного и того же числово
го выражения записать решение каждой задачи?
Запиши такое выражение. Будет ли стоимость второй
покупки в 2 раза больше, чем стоимость первой?
197. Как должна измениться цена товара для
того, чтобы стоимость той же покупки стала в 3 раза
больше, чем при прежней цене?
Щ Проверь свой вывод на примере стоимости яблок
45 руб. за 3 кг.
198. Как должна измениться стоимость покупки,
если цена товара уменьшится в 4 раза, а количество
останется тем же самым?
62
Когда стоимость одинаковая
199. Заверши в тетради заполнение данно
таблицы.
Вид товара Цена Количество Стоимость
Огурцы 20 руб./кг ? 100 руб.
Морковь ? 10 кг 100 руб.
Помидоры ? 4 кг 100 руб.
Персики 50 руб./кг ? 100 руб.
По данным таблицы определи, цена какого тонн
ра в 2 раза больше, чем цена помидоров.
По данным таблицы определи, количество какою
товара в 2 раза меньше, чем количество помидороп
Как ты думаешь, случайно ли оказалось, что при
ответе на эти два задания речь идёт об одном и
том же товаре?
!& ] Проверь замеченную зависимость величин для
зУю другой пары товаров (морковь и огурцы).
200. Прочитай следующее правило.
При одинаковой стоимости увеличение (умелп.
шение) количества в несколько раз приводи! к
уменьшению (увеличению) цены в это же число раз
Приведи пример из предыдущего задания, кою
рый подтверждает это правило.
63](https://image.slidesharecdn.com/42-170811133557/85/2-35-320.jpg)






![248. Какие из данных утверждений являются
верными? Докажи это. Перепиши верные утверж
дения в тетрадь. Я
а. В любом треугольнике есть острый угол.
б. В любом треугольнике есть прямой угол.
в. Если в треугольнике есть прямой угол, то это1
треугольник является прямоугольным.
г. Если в треугольнике есть острый угол, то этот
треугольник является остроугольным.
д. В любом четырёхугольнике есть острый угол.
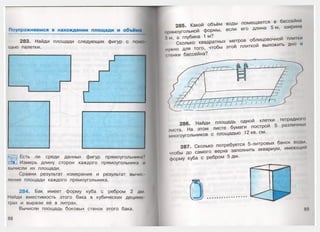
е. Если в четырёхугольнике есть прямой угол, то
этот четырёхугольник является прямоугольником.
ж. Если в четырёхугольнике все углы прямые, то
этот четырёхугольник является прямоугольником.
249. Коля всегда сидит за одной партой с
Витей или с Серёжей. Могут ли Витя и Серёжа
сидеть за одной партой, если все три мальчика
пришли на урок?
В каком случае Витя и Серёжа могут сидеть за
одной партой?
Может ли Петя сидеть за одной партой с
Серёжей, если на уроке присутствуют все четверо
названных мальчиков?
С кем в этом случае сидит Коля?
Ц р ] 250. Разгадайте арифметические ребусы.
Одинаковые буквы обозначают одинаковые цифры,
а разные буквы — разные цифры.
ТРИ _ АБББ СТОЛ
ТРИ А СТУЛ
ДЫРА ВВВ КЛАСС
76
Поупражняемся в вычислениях и повторим
пройденное _______________________ ______
251. Вычисли значения следующих выражений.
(236589 + 348967) - 361215 : 45
(452369-450864) • 16 - 23418 : 18
252. Реши задачу. Вычисли и запиши ответ.
Площадь первого земельного участка 2538 кв. м,
•по на 315 кв.м меньше, чем площадь второго уча<;|
ы, и в 3 раза больше, чем площадь третьего. Чему
раина площадь всех трёх участков?
253. Начерти прямоугольник, у которого одна
| трона в 4 раза больше и на 75 мм больше, чем
другая.
254. Длина стороны одного квадрата 8 см, а
другого — в 3 раза больше. Во сколько раз площадь
шорого квадрата больше, чем площадь первого?
255. Длины сторон первого прямоугольника 2 см
и 112 см, второго — 21 см и 21 см. Вычисли пери
мегр и площадь каждого прямоугольника. У какою
из прямоугольников периметр больше: у первого или
у второго? Площадь какого прямоугольника больше:
первого или второго?
256. Построй два таких прямоугольника, чтобы
периметр первого был больше, чем периметр второю,
а площадь первого была меньше, чем площадь вто
рого.
257. Выполни деление столбиком для следующих
пар чисел.
853 и 7 654 и 8 2783 и 5
527 и 12 327 и 32 2851 и 29
77 '](https://image.slidesharecdn.com/42-170811133557/85/2-42-320.jpg)







![Натуральные числа и число О (повторение)
323. Назови самое маленькое натуральное число.
Является ли число 0 натуральным?
Существует ли самое большое натуральное
число? Как это можно доказать?
Какое самое большое натуральное число ты мо
жешь назвать? Сколько «значным» является это число?
324. Запиши самое маленькое и самое большое
из пятизначных натуральных чисел. Сколько всего
существует пятизначных натуральных чисел? Как это
число можно вычислить?
325. Следующие числа запиши в порядке воз
растания.
23654 687369 96542 142578 68736
326. Следующие числа запиши в порядке убыва
ния.
389621 125369 96547 857931 84635
327. Назови натуральное число, которое находит
ся между числами 458963 и 458961. Запиши ответ с
помощью верного двойного неравенства.
328. Запиши все возможные числа с помощью
перестановки цифр в записи числа 123. Сколько
таких чисел у тебя получилось? Какое из этих чисел
будет самым большим? Каких чисел среди них боль
ше: чётных или нечётных?
100
|.'0. Определи, чётным или нечётным будет зна
Инин) Н1ЖДОГО из следующих выражений, не вычисляя
ежи жпчений.
(256897 + 23569) - (24563 + 57864)
(65342 + 75891) • (87562 + 56483)
:»:ю. Найди натуральное число, которое делится
нацело па числа 2, 3 и 5.
331. Найди натуральное число, которое мри
делении на 2, 3 и 5 даёт в остатке число 1.
|* 1 332. Значение какого из следующих выражении
||]р нпльзя вычислить? Почему?
и) (253471 + 325834) + (378964 - 378964)
0) (253471 + 325834) - (378964 - 378964)
и) (253471 +325834) • (378964-378964)
1) (253471 + 325834):(378964 - 378964)
Значение какого из оставшихся выражений легко
можно нычислить устно? Запиши это выражение и ого
лишение.
333. Найди натуральное число, которое является
нмIишачным и в котором число единиц в каждом
• и»«дующем разряде на 2 больше, чем в предыдущем
Сколько таких чисел существует?
Запиши эти числа.
334. Составь и запиши выражение, которое
• одержит все четыре действия и значение которою
ринно 1000.
101](https://image.slidesharecdn.com/42-170811133557/85/2-54-320.jpg)














