Документ объясняет аксиому математической индукции и примеры её применения для доказательства формул относительно натуральных чисел и их свойств. Рассматриваются теоремы о суммах, произведениях и делимости, а также приводятся конкретные примеры использования индукции для доказательства утверждений о числах. Кроме того, обсуждаются пифагоровы тройки и совершенные числа.

1. 301
В) Аксиома 8 называется аксиомой математической ин-
дукции. Она дает возможность доказывать общие утвержде-
ния о натуральных числах.
Пример 1. Докажем формулу Sn = a1
q
q
n
−
−
1
1
для суммы n
первых членов геометрической прогрессии с первым членом
a1 и знаменателем q.
Пусть n = 1. Тогда S1 = a1, так как сумма S1 состоит только
из одного числа a1. С другой стороны, данная формула дает:
S1 = a1
q
q
1
1
1
−
−
= a1
q
q
−
−
1
1
= a1, т. е. тот же результат. Можно сде-
лать вывод, что доказываемая формула истинна при n = 1.
Пусть формула истинна для n = k, т. е. истинна формула
Sk = a1
q
q
k
−
−
1
1
. Докажем, что при этом условии истинна и фор-
мула Sk + 1 = a1
q
q
k +
−
−
1
1
1
, полученная из доказываемой форму-
лы подстановкой k + 1 вместо n. Имеем:
Sk + 1 = a1 + a2 + … + ak + ak + 1 = (a1 + a2 + … + ak) + ak + 1 =
= Sk + ak + 1 = a1
q
q
k
−
−
1
1
+ a1qk
= a1
q
q
k
k
q
−
−
+
1
1
=
= a1
q q q
q
k k
− + −
−
1 1
1
( )
= a1
q q q
q
k k k
− + −
−
+
1
1
1
= a1
q
q
k +
−
−
1
1
1
,
т. е. получили ожидаемый результат. Таким образом, мы
установили, что из истинности утверждения для n = k следует
его истинность для n = k + 1.
Учитывая аксиому математической индукции, делаем вы-
вод о том, что формула Sn = a1
q
q
n
−
−
1
1
истинна при любом на-
туральном значении переменной n.
Пример 2. Докажем, что сумма квадратов первых n нечет-
ных натуральных чисел равна 1
3
n(2n − 1)(2n + 1), т. е. что
Sn = 12
+ 32
+ … + (2n − 1) = 1
3
n(2n − 1)(2n + 1).
Пусть n = 1. Тогда S1 = 1, так как первое нечетное нату-
ральное число — это число 1. Вместе с этим для значения вы-
ражения 1
3
n(2n − 1)(2n + 1) при n = 1 получим: 1
3
1(2 1 − 1)
(2 1 + 1) = 1
3
1 1 3 = 1, т. е. тот же результат.
Пусть утверждение истинно для n = k, т. е. истинна фор-
мула Sk = 1
3
k(2k − 1)(2k + 1). Докажем, что тогда утверж-
Правообладатель Народная асвета
Народная
асвета

2. 302
дение истинно и при n = k + 1, т. е. истинно равенство
Sk + 1 = 1
3
(k + 1)(2k + 1)(2k + 3).
Имеем:
Sk + 1 = 12
+ 32
+ … + (2k − 1)2
+ (2k + 1)2
=
= (12
+ 32
+ … + (2k − 1)2
) + (2k + 1)2
=
= 1
3
k(2k − 1)(2k + 1) + (2k + 1)2
= 1
3
(2k + 1)(k(2k − 1) + 3(2k + 1)) =
= 1
3
(2k + 1)(2k2
− k + 6k + 3) = 1
3
(2k + 1)(2k2
+ 5k + 3) =
= 1
3
(2k + 1)(2k + 3)(k + 1) = 1
3
(k + 1)(2k + 1)(2k + 3),
т. е. получили ожидаемый результат. Таким образом, мы
установили, что из истинности утверждения для n = k следует
его истинность для n = k + 1.
Учитывая аксиому математической индукции, де-
лаем вывод о том, что формула 12
+ 32
+ … + (2n − 1)2
=
= 1
3
n(2n − 1)(2n + 1) истинна при любом натуральном значе-
нии переменной n.
Есть утверждения о натуральных числах, которые истин-
ны не для всех натуральных чисел, а для тех, которые на-
чинаются с определенного числа. При доказательстве таких
утверждений также можно использовать аксиому математи-
ческой индукции, но первый этап доказательства — проверку
истинности утверждения для наименьшего натурального чис-
ла — начинают не с числа 1.
Пример 3. Докажем, что если натуральное число n не
меньше 5, то 2n
n2
.
Пусть n = 5. Тогда, подставив это значение переменной n
в неравенство 2n
n2
, получим неравенство 25
52
, которое
истинно.
Пусть при n = k, где k 4, неравенство 2n
n2
истинно,
т. е. истинно неравенство 2k
k2
. Докажем, что тогда истинно
и неравенство 2k + 1
(k + 1)2
.
Имеем 2k + 1
= 2 2k
. Учитывая допущение 2k
k2
, получим
2 2k
2 k2
. Значит, 2k + 1
2 k2
.
Докажем, что 2 k2
(k + 1)2
. Выполним равносильные
преобразования этого неравенства:
2 k2
(k + 1)2
≡ 2k2
k2
+ 2k + 1 ≡ k2
− 2k − 1 0 ≡
≡ (k2
− 2k + 1) − 2 0 ≡ (k − 1)2
− 2 0.
Но неравенство (k − 1)2
− 2 0 истинно, так как по условию
переменная k не меньше 5. Значит, истинно и неравенство
Правообладатель Народная асвета
Народная
асвета

3. 303
2 k2
(k + 1)2
. Учитывая, что 2k + 1
2 k2
, можем утверждать,
что 2k + 1
(k + 1)2
.
Аксиома математической индукции позволяет сделать вы-
вод о том, что неравенство 2n
n2
истинно при всех натураль-
ных значениях переменной n, не меньших 5.
? 1. Объясните смысл отношения непосредственного следования между
натуральными числами.
2. Сформулируйте аксиому математической индукции.
1098. Тройку чисел (a; b; c) называют пифагоровой, если
существует прямоугольный треугольник с катетами a и b и
гипотенузой c. Установите, являются ли пифагоровыми трой-
ками числа:
а) (5; 12; 13); д) (12; 35; 37);
б) (7; 24; 25); е) (9; 40; 41);
в) (6; 8; 12); ж) (20; 99; 101);
г) (20; 21; 29); з) (15; 112; 115).
1099. Найдите третье число пифагоровой тройки чисел, ес-
ли два из них следующие:
а) 11 и 60; б) 16 и 63; в) 13 и 84; г) 88 и 105.
1100. Натуральное число называется совершенным, если
оно равно сумме всех своих делителей, кроме самого числа.
Например, число 6 — совершенное, так как его не равные ше-
сти делители — это числа 1, 2, 3 и 6 = 1 + 2 + 3. Докажите, что
является совершенным число:
а) 28; б) 496; в) 8128; г) 33 550 336.
1101. Докажите иррациональность числа:
а) 5; б) 10; в) 23
; г) 54
.
1102. Выражением n! обозначается произведение всех на-
туральных чисел от 1 до n. Найдите значение выражения:
а) 6!; б) 10!; в) 12
10
!
!
; г)
13 8
10 8
! !
! !
.
−
+
1103. Сформулируйте признаки делимости на 2 и на 5 и
определите, делится ли на эти числа число:
а) 24 728; б) 142 745; в) 197 820; г) 345 777.
1104. Сформулируйте признаки делимости на 3 и на 9 и
определите, делится ли на эти числа число:
Правообладатель Народная асвета
Народная
асвета

4. 304
а) 24 729; б) 272 745; в) 197 820; г) 345 777.
1105. Найдите значение выражения:
а) 47 12 20 6 0 1 11
5
3
7
35
36
: : : , ;− −
б) 49 16 14 11 2 0 51
3
1
6
: : , : , ;− −
в) 3 3
4
: 7 21
4
2
3
− − 2 1 11
15
7
12
33
40
+ : ;
г) 5 3 2 251
12
11
24
− : , + 3 21
18
7
12
4
7
− .
1106. Найдите значение выражения:
а) ((8 + 4 (7 − 15) : 2 − 5) 4 − 11) : (2 − 9);
б) 2 0 2 1 1 9 0 3 1 0 8 8 10 0 033 8 101
5
1
4
, , , : , : ,− − − − − : 2;
в)
0 025 11
5
2 4 0 1
10 2 5
1
2
0 75
63
5
1 75
5
5 625
21
4
1 1 6
,
, ,
,
,
,
, : ,
:
−
+
−
−
−
+ + +
−−
−
0 25
33
4
11 0 5
,
: ,
1
9
.
1107. Докажите, что:
а) сумма n первых натуральных чисел равна
n n( )
;
+ 1
2
б) сумма n первых нечетных натуральных чисел равна n2
;
в) сумма n первых четных натуральных чисел равна
n(n + 1);
г) сумма n первых натуральных чисел, кратных трем, рав-
на 3
2
n(n + 1);
д) сумма n первых натуральных чисел, которые при делении
на 3 дают в остатке 1, равна 1
2
n(3n − 1);
е) сумма n первых натуральных чисел, которые при делении
на 3 дают в остатке 2, равна 3
2
n2
.
1108. Найдите и докажите формулу, выражающую сумму
n первых натуральных чисел, которые:
а) кратны трем;
б) при делении на 4 дают в остатке 1;
в) при делении на 4 дают в остатке 2;
г) при делении на 4 дают в остатке 3.
1109. Докажите, что сумма квадратов n первых натураль-
ных чисел равна
n n n( )( )
.
+ +1 2 1
6
Правообладатель Народная асвета
Народная
асвета

5. 305
1110. Докажите, что сумма квадратов первых n четных
натуральных чисел равна
4 2 1 2 1
3
n n n( )( )
.
− +
1111. Докажите, что сумма кубов первых n натуральных
чисел равна
n n2 2
1
4
( )
.
+
1112. Докажите, что при любом натуральном значении пе-
ременной n истинно равенство:
а) 1 − 22
+ 32
− 42
+ … + (−1)n − 1
n2
= (−1)n − 1 n n( )
;
+ 1
2
б) 1 2 + 2 3 + … + n(n + 1) =
n n n( )( )
;
+ +1 2
3
в) 1 4 + 2 7 + … + n(3n + 1) = n(n + 1)2
;
г) 1 2 3 + 2 3 4 + … + n(n + 1)(n + 2) =
n n n n( )( )( )
.
+ + +1 2 3
4
1113. Докажите, что:
а) при любых натуральных значениях переменных n и p
истинно равенство
1 2 … p + 2 3 … p(p + 1) + … + n(n + 1) … (n + p − 1) =
=
n n n n p
p
( )( )...( )
;
+ + +
+
1 2
1
б) при любом натуральном значении переменной n истин-
но равенство
2 12
+ 3 22
+ … + n(n − 1)2
+ (n + 1)n2
=
n n n n( )( )( )
.
+ + +1 2 3 1
1 3 4
1114. Докажите, что при любом натуральном значении пе-
ременной n истинно равенство:
а) 1 + 2 + 22
+ … + 2n − 1
= 2n
− 1;
б) 1 1! + 2 2! + … + n n! = (n + 1)! − 1;
в) (n + 1)(n + 2) … (n + n) = 2n
1 3 … (2n − 1).
1115. Докажите, что при любых натуральных значениях
переменных a и n истинно равенство:
а) 1
1a a( )+
+ 1
1 2( )( )a a+ +
+ … + 1
1( )( )a n a n+ − +
= n
a a n( )
;
+
б)
a + 1
2
+
a + 3
4
+
a + 7
8
+ … +
a n
n
+ −2 1
2
=
( )( )a n
n
− −1 2 1
2
+ n.
Правообладатель Народная асвета
Народная
асвета

6. 306
1116. Докажите, что на 9 делится:
а) сумма кубов трех последовательных натуральных чисел;
б) значение выражения 4n
+ 15n − 1 при любом натуральном
значении переменной n.
1117. Докажите, что при любом натуральном значении пе-
ременной на 64 делится значение выражения:
а) 32k − 1
+ 40k + 21;
б) 32l + 3
+ 40l − 27;
в) 4 32m + 2
+ 32m − 36.
1118. Докажите, что при любом натуральном значении пе-
ременной:
а) значение выражения 11n + 2
+ 122n + 1
делится на 133;
б) значение выражения 10p
+ 18p − 1 делится на 27;
в) значение выражения 32q + 3
− 26q − 27 делится на 169;
г) значение выражения 2r + 2
3r
+ 5r − 4 делится на 35.
1119. Докажите, что при любом четном значении перемен-
ной n значение выражения 20n
+ 16n
− 3n
− 1 делится на 323.
1120. Докажите, что при натуральном значении перемен-
ной, которое:
а) не меньше 3, истинно неравенство 2n
2n + 1;
б) не меньше 10, истинно неравенство 2n
n3
;
в) больше 2, истинно неравенство 2
1
2
1n n( )−
n!.
1121. Докажите, что при натуральном значении перемен-
ной, большем 1, истинно неравенство:
а) 1
1n +
+ 1
2n +
+ … + 1
2n
13
24
; в) 1
1
+ 1
2
+ … + 1
n
n;
б) 1
4
+ 1
9
+ 1
16
+ … + 1
2
n
1; г) 1
1
+ 1
2
+ … + 1
n
2 n.
1122. Докажите, что для любых целых положительных чи-
сел a1, a2, …, an истинно неравенство
a
a
1
2
+
a
a
2
3
+ … +
a
a
n
1
n.
1123. Докажите, что при любом натуральном значении пе-
ременной n, которое:
а) больше единицы, истинно неравенство 4
1
n
n +
( )!
( !)
;
2
2
n
n
б) не меньше 6, истинно неравенство n
n
2
n! n
n
3
.
Правообладатель Народная асвета
Народная
асвета

7. 307
44444
1124. Найдите значение выражения:
а) (( ( ) : ) )6 4 3 11 2 1 4 7+ − − − : (21 − 4);
б) 12 5 3 3 9 0 3 0 8 16 8 0 125 10 0 31 0 8 10 21
5
: , , , , , , , : ;− − − − −
в)
1 75 2
3
1 75 11
8
7
12
17
80
0 0325 400
, : , :
, :
−
−
: (6,79 : 0,7 + 0,3).
1125. С использованием формул сокращенного умно-
жения, в том числе и формулы a3
+ b3
= (a + b)(a2
− ab + b2
),
упростите выражение:
а) 2
2
6
4
4
22 2z s
s
s z z s− − +
+ − : 1
4
4
2 2
2 2
+
+
−
z s
z s
;
б) d e
d e
e
d d e de
d de
d e
e
d d e de e
−
− +
−
+ +
+
2 2
3 3 3 2 2
3 2
2 2
2
3 2 2 3
+ + +
+ ;
в)
l k
l k
l k
l k
l lk
l l k lk k
k
l k
−
+
+
−
+
+ − − +
− +
2 2 3 2
3 2 2 3
8 8
: 1
2
2
− l
k
;
г)
3 2
2 1
2 10
2 13 2
2
3 2
( )
( ) ( )
a
a a a
a a
a a a
+
+ + +
− −
− + −
+ : 5
1
3
2 1
3
2 12
a a a+ + −
+ −
( ) ( )
.
1126. Найдите значение выражения:
а) 1 +
− −
− −
+
−
q
q
z z
z z
s
s
при q = 3; s = 0,75; z = 1
2
;
б)
l k
l l k
−
+
3
−
l k
l k
−
+
при l = 1
16
; k = 1
81
.
1127. Решите уравнение:
а) 6
4 − p
= 25
1 3− p
− 16
4p −
;
б) 3 1 2
3 1
4
3
5
h h
h h
− − − −
− +
= 5h − 2;
в) 1
1 2
( )h +
+ 4
1 2
h h( )+
= 5
2 1h h( )
;
+
г)
2 19
5 52
y
y
+
−
− 17
12
y −
− 3
1 − y
= 0;
д)
3 3
2 22
e
e
−
−
−
2 2
3 6 32
e
e e
+
+ +
=
5 1
12 24 122
( )
;
e
e e
−
− +
е)
x
x
x
x+ −
+ =
1 1
45
16
2 2
.
Правообладатель Народная асвета
Народная
асвета

8. 308
1128. Решите систему уравнений:
а)
3 1
3 3
3 5
4
27 22
8
5 9
6
3 5
9
q a
a q
a q q
a q a
+ − = −
+ − = −
⎧
⎨
⎪
⎩
⎪
− +
− −
( )
,
;
б)
s d
d s
s d d
+
+ −
− − = +
+ =
⎧
⎨
⎪
⎩
⎪
2
4
1
3
3
6
2
2
1
3
,
;
в)
2 3
5
3 10
3
4 3
3
8 3
2
2 1 3
6
( )
,
;
z c c z
z c z c
z
− −
− −
+ + +
+
⎧
⎨
⎪
⎩
⎪
=
=
г)
f g f g
f g
g f
+ + −
− −
− =
− = −
⎧
⎨
⎪
⎩
⎪
1
3
2
4
2
5
3
4
3
3
2
( )
,
.
1129. Решите систему неравенств:
а)
( )( ) ,
;
a a a
a a
+ − +
+
⎧
⎨
⎪
⎩⎪
4 2 1 2
6 42
б)
( )( ) ( ),
;
x x x
x x
− + −
+ −
⎧
⎨
⎪
⎩⎪
3 2 5 5 4
6 7 02
в)
( )( ) ( )( ),
;
x x x x
x x
− + − +
− −
⎧
⎨
⎪
⎩⎪
3 2 5 4 2 3
6 7 02
г)
( )( ) ( )( ),
.
2 3 2 5 5 2
6 7 02
t t t t
t t
− + − +
− −
⎧
⎨
⎪
⎩⎪
1130. Найдите площадь прямоугольника с периметром 72,
диагонали которого пересекаются под углом 60°.
1131. Медиана прямоугольного треугольника длиной m
делит его прямой угол в отношении 1 : 2. Найдите площадь
треугольника.
1132. Гипотенуза прямоугольного треугольника равна c, а
один из его углов — 30°. Найдите радиус окружности с цент-
ром в вершине этого угла, которая делит данный треугольник
на две равновеликие части.
1133. Докажите, что сумма расстояний от любой точки осно-
вания равнобедренного треугольника до его боковых сторон рав-
на высоте этого треугольника, проведенной к боковой стороне.
Правообладатель Народная асвета
Народная
асвета

9. 309
1134. Найдите острый угол ромба, сторона которого яв-
ляется средним геометрическим его диагоналей.
1135. Диагонали выпуклого четырехугольника равны a и b,
а отрезки, соединяющие середины противоположных сто-
рон, равны друг другу. Найдите площадь четырехугольника.
1136. Найдите площадь четырехугольника, ограниченно-
го всеми биссектрисами параллелограмма со сторонами a и b
и углом α.
1137. Из Сенно в Богушевск выехал велосипедист, а через
некоторое время ему навстречу из Богушевска — второй вело-
сипедист, после чего велосипе-
дисты сближались со скорос-
тью 36 км/ч, а когда встрети-
лись, то оказалось, что второй
велосипедист не доехал 1 км до
Оболи, а первый был в дороге
1 ч 15 мин (рис. 399). Найдите
расстояние от Сенно до Оболи, учитывая, что средняя ско-
рость движения велосипедистов оказалась равной 17,5 км/ч.
1138. Есть три вида коробок для укладывания конфет.
В первой из них 6 рядов, вторая всего вмещает 12 конфет,
а если сложить количество конфет в одном ряду обеих ко-
робок, то получится 11. Третья коробка имеет столько рядов,
сколько их вместе в первой и второй коробках, вмещает
в одном ряду 6 конфет, а всего — столько конфет, сколько их
вмещают первая и вторая коробки вместе (рис. 400). Найдите
количество рядов конфет в третьей коробке.
Рис. 399
Рис. 400
Правообладатель Народная асвета
Народная
асвета

10. 310
1139. Есть три цилиндра. Пло-
щадь основания одного из них рав-
на 9 см2
, объем второго — 121 см3
, а
если поставить первый цилиндр на
второй, то получится тело высотой
18 см. Третий цилиндр имеет вы-
соту 9,2 см, площадь его основания
равна сумме площадей оснований
первого и второго цилиндров, а его
объем — их суммарному объему
(рис. 401). Найдите объем третьего
цилиндра, учитывая, что объем V
цилиндра находится по формуле V = S H, где S — площадь
основания цилиндра, а H — его высота.
* * *
1140. Докажите, что при целых m, больших 2, уравнение
x3
− mx + 1 = 0 не имеет рациональных корней.
1141. Как восстановить пятиугольник по известным се-
рединам его сторон?
1142. Есть ли такие 4 натуральных числа, чтобы наимень-
шие общие кратные их пар были последовательными числами?
26. Логические основы алгебры
Алгебра возникает из арифметики с введением неизвестной
величины — переменной. Действия над ней, указанные усло-
вием задачи, приводят к уравнению, из которого находится
неизвестная. Такой подход в неявной форме можно усмо-
треть уже в древнеегипетском папирусе Ринда (около 2000 до
н. э.), где искомая величина называлась словом куча и обо-
значалась соответствующим иероглифом. Из клинописных
математических текстов Древнего Вавилона стало известно,
что вавилоняне умели решать разнообразные задачи, причем
некоторые из них сводятся к квадратным уравнениям.
Понятно, что в те времена арифметика и алгебра не были
отделены друг от друга и древняя математика была единой.
В Древней Греции отчетливо выделилась геометрия, которая
нашла свое определенное завершение в Началах Евклида, где
геометрия была изложена аксиоматически. Влияние этого ме-
тода было настолько большим, что многие проблемы переводи-
Рис. 401
Правообладатель Народная асвета
Народная
асвета

11. 311
лись на геометрический язык: величины истолковывались как
длины отрезков, произведение величин — как площадь прямо-
угольника и т. д. Результаты развития арифметики и в ней ал-
гебры подытожены в Арифметике Диофанта, где он уже доволь-
но свободно оперирует уравнениями первой и второй степени
и в зародышевой форме пользуется отрицательными числами.
Достижения древнегреческой науки были восприняты уче-
ными средневекового Востока, среди которых заметное место
занимали ученые Средней Азии. Один из них — аль-Хорезми
(787—850) (рис. 402), который в своей алгебраической рабо-
те Краткая книга пополнения и противопоставления ал-
гебру впервые рассматривает как самостоятельную ветвь ма-
тематики, систематически решает уравнения первой и второй
степени. Этот трактат долгое время был основной книгой по
алгебре в странах Европы, а название операции аль-джебр, ко-
торая заключалась в переносе члена уравнения из одной части
в другую с изменением его знака, позже стало названием Алге-
бра соответствующего раздела математики. Имя аль-Хорезми
(латинизированное Algorithmi) вошло в
математику как общее название Алго-
ритм любой системы вычислений, вы-
полняемых по определенным правилам.
Математики средневекового Востока
изложение вели словами. Дальнейший
прогресс стал возможным, когда в об-
щее употребление вошла удобная сим-
волика. Этот процесс был длительным
и извилистым. Современный алгебраи-
ческий аппарат сложился в основном к
концу XVI в. и был окончательно закреп-
лен французским математиком Ф. Вие-
том (1540—1603) (рис. 403). В 1591 г. он
впервые вводит буквенные обозначения
не только для неизвестных величин, что
уже делалось и ранее, но и для данных,
т. е. для коэффициентов уравнений.
Это позволило выражать свойства урав-
нений и их корней общими формула-
ми, а сами выражения с переменными
стали объектами, над которыми мож-
но выполнять те или иные действия. Рис. 403
Рис. 402
Правообладатель Народная асвета
Народная
асвета

12. 312
Важным этапом в развитии алгебры
стало введение отрицательных чисел.
До этого даже уравнение первой сте-
пени не всегда имело решение. Решаю-
щий шаг — пользование отрицательны-
ми числами — был сделан в X в. индий-
скими математиками. В Европе отри-
цательные числа утвердились только
в XVII в. после того, как французский
философ и математик Р. Декарт (1596—
1650) (рис. 404) использовал их нагляд-
ное геометрическое представление для аналитической геоме-
трии, в которой геометрические образы — линии, поверхно-
сти — получают алгебраическое истолкование уравнениями.
К концу XVIII в. алгебра сложилась примерно в том объеме,
в котором она и теперь преподается в школе.
Основным объектом изучения школьной алгебры является
выражение с переменными, которое образуется из чисел и пере-
менных с помощью действий. Другие объекты изучения школь-
ной алгебры — уравнение, неравенство, числовая функция —
вводятся на основании понятия выражения с переменными.
Уравнение F = G образуется из двух выражений F и G с по-
мощью отношения равно, а неравенства F G, F G, F ≠ G,
F G, F G образуются из этих выражений с помощью от-
ношений меньше, больше, не равно, не больше, не меньше.
Функция y = f(x) возникает, когда по отношению к выраже-
нию f(x) ставится вопрос о том, как себя ведут значения y вы-
ражения f(x) в зависимости от значений переменной x.
В школе выражения рассматриваются на множестве дейст-
вительных чисел, выступающем в качестве области значений
переменной. Свойства выражения определяют те действия,
которые использованы при его образовании. Вы изучали дей-
ствия сложения, вычитания, умножения, деления, возведе-
ния в степень, извлечения корня, нахождения значений си-
нуса, косинуса, тангенса и котангенса. В основе этого набора
действий лежат действия сложения и умножения. Например,
возведение в степень определяется следующим образом:
Рис. 404
Правообладатель Народная асвета
Народная
асвета

13. 313
an
= a a a
n
...
множителей
1 24 34
, если a — любое действительное число и
n — натуральное число;
a1
= a, если a — любое действительное число;
a0
= 1, если a — не равное нулю действительное число;
a−n
= 1
аn
, если a — не равное нулю действительное число
и п — натуральное число.
Таким образом, в качестве исходных понятий школьного
курса алгебры целесообразно принять понятия: действитель-
ное число; переменная; сложение; умножение.
Действия вычитания и деления, отношение больше между
числами вводятся определениями:
а − b обозначает такое число c, что a = b + c;
а : b обозначает такое число c, что a = bc;
a b означает, что a − b 0.
Аксиомы описывают действия сложения, вычитания,
умножения и деления, а также отношение больше.
а) Свойства сложения и вычитания
1) a + b = b + a (переместительность сложения);
2) a + (b + c) = (a + b) + c (сочетательность сложения);
3) a + 0 = a (свойство нуля при сложении);
4) a + (−a) = 0 (свойство противоположного числа);
5) a − b = a + (−b) (связь вычитания со сложением);
6) если a b, то a + c b + c (монотонность сложения).
б) Свойства умножения и деления
7) a b = b a (переместительность умножения);
8) a (b c) = (a b) c (сочетательность умножения);
9) a 1 = a (свойство единицы при умножении);
10) a 0 = 0 (свойство нуля при умножении);
11) −a = (−1) a (представление противоположного числа
произведением);
12) если a ≠ 0, то 1
а
a = 1 (свойство обратного числа);
13) если b ≠ 0, то a
b
= 1
b
a (представление дроби произ-
ведением);
14) a (b + c) = ab + ac (распределительность умножения
по отношению к сложению);
15) если a b и c 0, то a c b c (монотонность умно-
жения).
Правообладатель Народная асвета
Народная
асвета

14. 314
в) Свойства порядка
16) если a, b — действительные числа, то или a b, или
a = b, или a b (линейная упорядоченность);
17) если a b, то найдется такое число c, что a c b
(плотность множества действительных чисел);
18) если a b и b c, то a c (транзитивность отноше-
ния меньше).
г) Архимедово свойство
19) Для любого действительного числа x найдется такое
натуральное число n, что n x.
д) Свойство непрерывности множества действительных
чисел
20) Любая система вложенных отрезков [an; bn] (рис. 405),
длины которых стремятся к нулю, когда n неограниченно уве-
личивается, имеет общую точку.
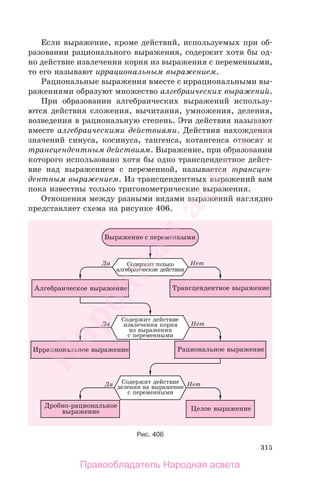
Свойства а)—д), по существу,
составляют полную систему ак-
сиом для действительных чисел,
а свойства а)—г) — полную си-
стему аксиом для рациональных
чисел. В курсах арифметики и алгебры вы познакомились со
всеми свойствами а)—г) и использовали их при доказывании
правил тождественных преобразований выражений, установ-
лении правил равносильных преобразований уравнений.
В школьном курсе алгебры вы изучали разные классы
выражений с переменными, которые определяются набором
действий, используемых при их образовании.
Если выражение с переменными образовано с помощью дей-
ствий сложения, вычитания, умножения, возведения в нату-
ральную степень и деления на число, то его называют целым
выражением. Каждое целое выражение равносильными пре-
образованиями можно свести к многочлену стандартного вида.
Если выражение, кроме действий, используемых при об-
разовании целого выражения, содержит хотя бы одно дейст-
вие деления на выражение с переменными, то его называют
дробно-рациональным выражением.
Целые выражения вместе с дробно-рациональными вы-
ражениями образуют множество рациональных выражений.
Любое рациональное выражение равносильными преобразова-
ниями можно свести к рациональной дроби или целому вы-
ражению.
Рис. 405
Правообладатель Народная асвета
Народная
асвета

15. 315
Если выражение, кроме действий, используемых при об-
разовании рационального выражения, содержит хотя бы од-
но действие извлечения корня из выражения с переменными,
то его называют иррациональным выражением.
Рациональные выражения вместе с иррациональными вы-
ражениями образуют множество алгебраических выражений.
При образовании алгебраических выражений использу-
ются действия сложения, вычитания, умножения, деления,
возведения в рациональную степень. Эти действия называют
вместе алгебраическими действиями. Действия нахождения
значений синуса, косинуса, тангенса, котангенса относят к
трансцендентным действиям. Выражение, при образовании
которого использовано хотя бы одно трансцендентное дейст-
вие над выражением с переменной, называется трансцен-
дентным выражением. Из трансцендентных выражений вам
пока известны только тригонометрические выражения.
Отношения между разными видами выражений наглядно
представляет схема на рисунке 406.
Выражение с переменными
Да Нет
Да Нет
Да Нет
Рис. 406
Правообладатель Народная асвета
Народная
асвета

16. 316
? 1. Как из выражений с переменными образуется уравнение; неравен-
ство?
2. Как понятие числовой функции связано с понятием выражения с
переменными?
3. Как действие вычитания и отношение больше определяются через
действие сложения?
4. Как действие деления определяется через действие умножения?
5. Как определяется действие возведения в степень?
6. С помощью каких действий образуется целое выражение и к ка-
кому виду такое выражение можно свести тождественными преобра-
зованиями?
7. С помощью каких действий образуется дробно-рациональное вы-
ражение?
8. Какие выражения составляют множество рациональных выражений
и к какому виду можно свести тождественными преобразованиями ра-
циональное выражение?
9. С помощью каких действий образуется иррациональное выражение?
10. Какие выражения составляют множество алгебраических выраже-
ний и с помощью каких действий они образуются?
11. Какие действия называют алгебраическими, какие — трансцен-
дентными?
1143. Сформулируйте известные вам правила проверки вы-
читания сложением и вычитанием. Запишите их с помощью
переменных и проиллюстрируйте на примере 25 − 17 = 8.
1144. Сформулируйте известные вам правила проверки
деления умножением и делением. Запишите их с помощью
переменных и проиллюстрируйте на примере 200 : 8 = 25.
1145. Сформулируйте правило проверки действия из-
влечения корня действием возведения в степень. Запишите
его с помощью переменных и проиллюстрируйте на примере
34
= 81.
1146. Найдите значение выражения 96 1
2
1п−
при значе-
нии переменной п, равном:
а) −5; б) −1; в) 0; г) 2; д) 7; е) 10.
1147. Запишите в виде степени с основанием 2 выражение:
а) 16 2п
; в) 85
4п
; д) 8
4
2
3
п
п
−
−
;
б) 8 2п− 1
; г) 163
4п − 8
; е) 32
4
2 1
5 3
п
п
−
−
.
1148. Установите, существует ли такое значение пе-
ременной x, при котором функция, заданная формулой
y = 4x2
− 5x + 7, принимает значение, равное:
а) 3; б) 6.
Правообладатель Народная асвета
Народная
асвета

17. 317
1149. Графиком функции f служит луч с началом в точке
A(3; 5), параллельный оси х и расположенный в первом ко-
ординатном угле. Постройте этот график и укажите область
определения и область значений функции.
1150. Установите, может ли функция y = x2
+ 14x + 15 при-
нимать значение, равное:
а) −1; б) −3; в) −5.
1151. Преобразуйте произведение (b − 10)(b2
+ 10b + 100) в
многочлен стандартного вида:
а) по правилу умножения многочлена на многочлен;
б) по формуле (x − y)(x2
+ xy + y2
) = x3
− y3
.
1152. Преобразуйте в многочлен стандартного вида про-
изведение:
а) (x − 2)(x2
+ 2x + 4); г) (2a + 1)(4a2
− 2a + 1);
б) (p − 5)(p2
+ 5p + 25); д) (10m − 3n)(100m2
+ 30mn + 9n2
);
в) (y + 4)(y2
− 4y + 16); е) (4u + 5v)(16u2
− 20uv + 25v2
).
1153. Представьте произведением многочлен:
а) p6
+ q6
; в) k6
− 1; д) a6
− 64;
б) m6
− n6
; г) l6
+ 1; е) 64c6
− d6
.
1154. Запишите произведением двучлена и трехчлена вы-
ражение:
а) (r + 6)3
− 1; в) (t + 3)3
− 64;
б) (s − 2)3
+ 27; г) a3
+ (a − b)3
.
1155. Докажите тождество
(x − y)(xn − 1
+ xn − 2
y + xn − 3
y2
+ … + x2
yn − 3
+
+ xyn − 2
+ yn − 1
) = xn
− yn
и, используя его, запишите многочленом выражение:
а) (a − 1)(a5
+ a4
+ a3
+ a2
+ a + 1);
б) (b − 2)(b3
+ 2b2
+ 4b + 8);
в) (c − 3)(c4
+ 3c3
+ 9c2
+ 27c + 81);
г) (d − 4)(d5
+ 4d4
+ 16d3
+ 64d2
+ 256d + 1024).
1156. Сократите дробь:
а)
х
х
5
1
1
−
−
; б)
у
у
7
1
2 2
−
−
.
Правообладатель Народная асвета
Народная
асвета

18. 318
1157. Преобразуйте в многочлен стандартного вида вы-
ражение:
а) (u − 4)(u2
+ 4u + 16); в) (w − 1)(w3
+ w2
+ w + 1);
б) (v + 10)(v2
− 10v + 100); г) (q − r)(q3
+ q2
r + qr2
+ r2
).
1158. Дайте определения дей-
ствиям нахождения значений
синуса угла, косинуса угла, тан-
генса угла и котангенса угла и
объясните, почему они сводятся
к действию умножения. Начер-
тите в тетради такой же угол,
как на рисунке 407. Выполните
необходимые построения и изме-
рения и найдите приближенное
значение синуса, косинуса, тан-
генса и котангенса этого угла.
1159. Есть выражения:
x; a + b
4
; a + b
u + 2
; x + 2x2
; t + sin t;
47; v2
− 1
23
; v2
− 1
3
v
; z; sin α;
5 1
3
; cos ;a b+6 1 − 2
3tg
; 1 − 2
2tg β
;
y
7
4 .
Какие из них являются:
а) числовыми выражениями;
б) выражениями с переменными;
в) целыми выражениями;
г) дробно-рациональными выражениями;
д) рациональными выражениями;
е) иррациональными выражениями;
ж) алгебраическими выражениями;
з) трансцендентными выражениями?
44444
1160. Упростите выражение:
а) (2q − 3y)(3q − 2y); д) (f + g)2
(f − g);
б) (e + r + t)(e + r − t); е) (h2
− j2
) h
j
j
h
+ ;
в) (y3
− y2
b + yb2
− b3
)(y + b); ж) 2
3
5
4
k
l
l
k
− 3
2
4
5
k
l
l
k
+ ;
г) (z − 1)(z − 2)(z − 3); з) (s + d) 1 1
s d
− .
Рис. 407
Правообладатель Народная асвета
Народная
асвета

19. 319
1161. Разложите на множители выражение:
а) s3
+ s2
− s − 1; е) m4
+ m2
n2
+ n4
;
б) t4
− t3
− t + 1; ж) (q2
+ qd − d2
)2
− (q2
− qd − d2
)2
;
в) d5
− d4
− d + 1; з) s2
d2
+ r2
t2
− s2
r2
− d2
t2
+ 4sdrt;
г) e2
− 7er + 12r2
; и) x2
− 6xk + 8k2
+ 2kl − l2
.
д) 3z2
f2
− z4
− f4
;
1162. Упростите выражение:
а)
er tr ei ti
er tr ei ti
− + −
+ + +
; д)
a a a
a a
3 2
4 2
1
2 1
− − +
− +
;
б)
jh jg h hg
jf jd hf hd
+ + +
+ + +
2
; е)
1 3 3 2 3
− + −
− + −
c c c
b bc p pc
;
в)
( )
;
j g f
j g f
+ −
+ +
2 2
ж)
z xz yz xy
z yz xz xy
2
3 2
− + −
+ + +
;
г)
t r t r
t r t r
i i i i
i i i i
+ − − +
+ − − +
−
−
2 2 2 2
1 1 1 1
; з)
a a a
a a a a
p p p
p p p p
+ −
+ + − −
− +
− + −
2 2
2 1 1 2
2
.
1163. Упростите выражение:
а) 1
1 + p
+ 1
1 − p
−
2
1 2
p
p−
;
б)
e
e
+
−
1
2 2
−
e
e
−
+
1
2 2
− 4
12
e
e −
+
e
e
2
2
1
1
+
−
;
в)
t y
t ty t
+
− +2 2
−
2
3 3
ty
t y+
;
г)
6 6
2 2
r e
re r
+
+
+ 8
2e r−
−
4 2
42 2
r e
e r
+
−
;
д)
p
p q2 2
+
−
q
p q2 2
−
+
pq p q
p q
( )
;
+
−4 4
е) 2(l − k) +
l k
l k
2 2
+
+
;
ж) 2j + h −
2 32 3
2 2
jh h
j h
+
+
;
з)
g f
g f
2 2
+
−
− 3(g + f).
1164. Найдите значение выражения:
а) 1 12
1 3
9 9
3 1
2
− −
−
−
+q
q q
q
: (2 (1 − 9q2
)) при q = − 1
2
;
б) 2
s
−
s
s s s s
+
− + + −
− −
1
1
1
1
2
13 2
:
s s s
s
3 2
2
2
1
+ +
−
при s = 11
2
;
Правообладатель Народная асвета
Народная
асвета

20. 320
в) 3
2
−
( , )0 5 1
1
1
2 2
1
13 2
d d
d d d d
+
− − + +
+ +
d d d
d
3 2
1
+ +
−
при d = 2,5;
г)
z x
z x z zx
zx
z
z x
+
+ − −
+
−
+ +3 2 2
1
1
1
: ( )
z x
x
3 3
2
3 3
+
−
при x = 1 и z = − 3
2
.
1165. Упростите выражение:
а) m
n m
n
+
+ n
n m
m
−
− − n
n m
m
+
+ m
n m
n
−
− ;
б) 1
e e r e t( )( )− −
+ 1
r r e r t( )( )− −
+ 1
t t e t r( )( )
;
− −
в)
1
s d
s f
−
−
+
1
d f
d s
−
−
+
1
f s
f d
−
−
;
г)
g
g h
g j
g
−
−
+
h
h j
h g
h
−
−
+
j
j g
j h
j
−
−
.
1166. Решите неравенство:
а) (m + 2)(m + 5) 0; д) (c + 1)(1 − c) c + 1;
б) z(−2 − z) 0; е) (b − 3)(5 − b) 4b − 12;
в) (x + 1)(2 − 5x) 0; ж) (2n + 5)(5n + 2)(n2
− 1) 0;
г) (3 − 2a)(−1 + a) 0; з) (k − 5)(3 − 5k)(k2
− 2)2
0.
1167. Решите уравнение:
а) (x2
− 3x + 1)2
+ 4(x2
− 3x + 1) = 5;
б) (x2
+ 2x + 3)2
− (x2
+ 2x + 3) − 6 = 0;
в) 2(2x2
− 5x + 1)2
= 2x2
− 5x − 5;
г) (2x2
− 3x + 1)2
+ 3(3x − 1) = 6x2
.
1168. Решите систему уравнений:
а)
( )( ) ,
;
s d
s
d
− − =
=
⎧
⎨
⎪
⎩⎪
−
−
2 3 1
1
2
3
в)
3 2
5
2
4
h
j
j
h
h j
−
+
+ =
− =
⎧
⎨
⎪
⎩⎪
,
;
б)
f
g f f g
g f
g f
+
− −
−
+
=
=
⎧
⎨
⎪
⎩
⎪
3
3 3
1
2
2
5
( )( )
,
;
г)
2 5
2
2 3
1
2
3 4 1
k
k
l
l
k l
−
−
−
−
+ =
− =
⎧
⎨
⎪
⎩⎪
,
.
Правообладатель Народная асвета
Народная
асвета

21. 321
1169. Решите систему уравнений:
а)
( )( ) ,
;
x y
x
y
+ − = −
= −
⎧
⎨
⎪
⎩⎪
+
−
2 1 2
2
2
1
в)
c m
c m
m
m
c
+ =
− =
⎧
⎨
⎪
⎩⎪
−
+
3
3
2
2
,
;
б)
m n
m n
m n n m
m n
+
−
− +
+ +
=
=
⎧
⎨
⎪
⎩
⎪
2 1
4
2 2
1
7
3
,
;
( )( )
г)
3 2 1
1
3 5
1
5 1
1
z a
z
a
a
z
− =
+ =
⎧
⎨
⎪
⎩⎪
−
+
−
+
,
.
1170. Решите систему уравнений:
а)
1 1 3
2
1 1 5
42 2
p t
p t
+ =
+ =
⎧
⎨
⎪
⎩
⎪
,
;
в)
s d
s
d
2 2
625
4
3
+ =
=
⎧
⎨
⎪
⎩⎪
,
;
б)
1 1 1
3
2 2
160
l k
l k
+ =
+ =
⎧
⎨
⎪
⎩⎪
,
;
г)
z
c
z c
2
2
4
25
2 5
=
− = −
⎧
⎨
⎪
⎩⎪
,
.
1171. Решите неравенство:
а) 2 5x + 5; г) 3 5+ x 3;
б) 3 2x − 1; д) − −2 3x −2;
в) 5 4− x 3; е) − +2 5x −3.
1172. Решите систему неравенств:
а)
x
x x
−
− +
⎧
⎨
⎪
⎩⎪
2 3
4 3 82
,
;
в)
x
x x
−
− +
⎧
⎨
⎪
⎩⎪
3 2
7 20 82
,
;
б)
x
x x
+
− +
⎧
⎨
⎪
⎩⎪
3 2
2 5 3 102
,
;
г)
x
x x
−
− − +
⎧
⎨
⎪
⎩⎪
1 3
4 3 72
,
.
1173. Докажите тождество
(x − y)(xn − 1
+ xn − 2
y + xn − 3
y2
+ … + xyn − 2
+ yn − 1
) =
= xn
− yn
и, используя его, запишите многочленом выражение:
а) (c − 3)(c4
+ 3c3
+ 9c2
+ 27c + 81);
б) (a + 1)(a5
− a4
+ a3
− a2
+ a − 1);
в) (b + 2)(b3
− 2b2
+ 4b − 8).
Правообладатель Народная асвета
Народная
асвета

22. 322
1174. Докажите, что биссектриса прямого угла прямо-
угольного треугольника делит пополам угол между медианой
и высотой, проведенными к гипотенузе.
1175. Точка гипотенузы прямоугольного треугольника,
равноудаленная от катетов, делит гипотенузу на отрезки дли-
ной 30 и 40. Найдите длины катетов.
1176. Когда в ромб с острым углом 45° вписали окруж-
ность, то ее радиус оказался равным 2. Найдите произведение
диагоналей ромба.
1177. В ромб с высотой h и острым углом α вписана
окружность. Найдите радиус большей из двух возможных
окружностей, каждая из которых касается данной окружно-
сти и двух сторон ромба.
1178. Сторона PS прямоугольника PQRS в три раза боль-
ше стороны PQ, а точки A и B делят сторону PS на три доли.
Найдите сумму углов PAQ, PBQ и PSQ.
1179. Общая хорда двух пересекающихся окружностей
равна а и является стороной правильного шестиугольника,
вписанного в одну окружность, и правильного треугольника,
вписанного в другую. Найдите расстояние между центрами
окружностей.
1180. В остроугольный треугольник с площадью 3 впи-
сан такой квадрат, что одна его сторона лежит на сто-
роне треугольника длиной 3, а противоположная со-
единяет точки на двух других сторонах. Найдите площадь
квадрата.
1181. Найдите площадь треугольника DEF, в котором сто-
рона DE равна 20, а медианы, проведенные к сторонам EF и
DF, равны 18 и 24.
1182. Торонто, Монреаль, Калгари, Эдмонтон, Винни-
пег — крупнейшие города Канады. Уменьшенное на 11 тыс. чел.
население Торонто относится к увеличенному на 10 тыс. чел.
населению Эдмонтона как 40 : 11, а к увеличенному на
1 тыс. чел. населению Монреаля — как 32 : 13. Уменьшен-
ное на 1 тыс. чел. население Калгари относится к увеличен-
ному на 1 тыс. чел. населению Монреаля как 54 : 65, а к уве-
личенному на 1 тыс. чел. населению Виннипега — как 72 : 53.
Найдите население этих городов Канады, учитывая, что на-
селение Торонто на 31 тыс. чел. больше учетверенного на-
селения Виннипега.
Правообладатель Народная асвета
Народная
асвета

23. 323
* * *
1183. Есть 30 таких чисел b1, b2, b3 …, b30, что
b1 b2 b3 … b30. Найдите такую последовательность a1, a2,
a3, …, a30 их расположения, чтобы сумма a a1 2− + a a2 3− +
+ a a3 4− + … + a a29 30− + a a30 1− была наибольшей.
1184. На стороне BC треугольника ABC выбрали точку K
так, что отрезок AK пересекает медиану BM в точке N, для
которой AN = BC. Докажите, что BK = KN.
1185. В окружность вписан неправильный n-угольник, ко-
торый при повороте вокруг центра на угол, отличный от 360°,
совмещается сам с собой. Докажите, что число n составное.
27. Логические основы геометрии
Геометрия — часть математики, которая изучает про-
странственные формы и отношения.
Первичные геометрические представления появились на
самых ранних этапах развития общества и постепенно рас-
ширялись и уточнялись в связи с усложнением практической
деятельности, в процессе которой людям приходилось оце-
нивать расстояния, стрелы и копья делать прямыми, срав-
нивать их по длине и др. Но сама геометрия зародилась тог-
да, когда развитие земледелия заставило людей выработать
первые правила: измерения земельных участков; нахожде-
ния объемов емкостей; возведения строений и др. Эти пра-
вила сравнения фигур, нахождения геометрических величин,
простейших геометрических построений составили начала
геометрии как прикладной науки. Такая практическая гео-
метрия складывалась в древних земледельческих обществах
в Египте, Вавилоне, дельте Инда, Китае. Самый ранний до-
кумент, содержащий геометрические сведения, дошел до нас
из Египта и относится к XVII в. до н. э. Этот и более поздние
документы свидетельствуют о том, что египтяне знали мно-
го геометрических фактов, например теорему Пифагора, при-
ближенное представление объема шара через его радиус, но
это были именно факты. Математика в нашем нынешнем по-
нимании оформилась значительно позже.
В VII в. до н. э. геометрические знания египтян были
усвоены учеными Древней Греции, где на протяжении не-
скольких столетий пополнились многими новыми фактами.
Эти факты постепенно упорядочивались, складывались в си-
Правообладатель Народная асвета
Народная
асвета

24. 324
стему, одни факты стали выводиться
из других. Формировалась процеду-
ра доказывания, и этим самым факты
превращались в теоремы, т. е. предло-
жения, которые устанавливаются рас-
суждениями без ссылок на опыт. Ста-
ли появляться задачи, имеющие чисто
теоретическое значение, например зада-
ча построения геометрической линейкой
и циркулем квадрата, равновеликого
данному кругу, начали оформляться
представления об идеальных геометри-
ческих фигурах — точке без измере-
ний, линии без ширины и толщины,
поверхности без толщины и т. п. Гео-
метрия постепенно становится наукой
в нынешнем понимании этого слова.
Воспроизвести процесс становления гео-
метрической науки в деталях невозмож-
но, но известны многие древние ученые,
которые его определяли, среди них Фалес
(624—547 до н. э.) (рис. 408) и Пифагор
(580—500 до н. э.) (рис. 409). В конце V в.
до н. э. греческий геометр Гиппократ
Хиосский создал первое систематическое произведение по
геометрии, которое, однако, до нас не дошло.
Одним из важнейших событий того времени было откры-
тие несоизмеримых отрезков: диагональ квадрата и его сторо-
на не имеют общей меры, т. е. ни один отрезок, каким бы ма-
лым он ни был, не укладывается целое количество раз как на
стороне, так и на диагонали. Прежнее представление о том,
что отношение любых величин можно выразить рациональ-
ным числом, т. е. отношением натуральных чисел, оказалось
неправильным. Обобщить понятие числа введением клас-
са иррациональных чисел греки не смогли. Поэтому то, что
мы теперь выражаем средствами алгебры, греки выражали
геометрически. Например, квадратное уравнение x2
+ ax = b
представлялось так: найти такой отрезок x, чтобы построен-
ный на нем квадрат вместе с прямоугольником, построенным
на этом отрезке и данном отрезке a, имели площадь, равную
данной площади b. Вместо действительных чисел рассматри-
вались отношения величин, теорию которых в IV в. до н. э.
построил Евдокс (около 408 — около 355 до н. э.) (рис. 410).
Рис. 409
Рис. 408
Правообладатель Народная асвета
Народная
асвета

25. 325
Достижения геометрической науки
были систематизированы Евклидом в
работе, известной под названием Нача-
ла. Здесь геометрия представлена так,
как понимается и теперь элементарная
геометрия: наука о пространственных
формах и отношениях, развертывающа-
яся в логической последовательности
на основании явно сформулированных
основных положений — аксиом. Теперь
эту науку называют евклидовой гео-
метрией. Геометрия после Евклида еще в Древней Греции
исследованиями Архимеда (около 287 — 212 до н. э.), Апол-
лония Пергского (около 260 — 170 до н. э.), Гиппарха (около
180 — 125 до н. э.), Менелая (I в.) обогащается новыми фак-
тами. Дальнейшее развитие геометрии замедлилось без но-
вых идей и методов. Они появились только в III в. в работах
Диофанта, математиков Индии, Средней Азии, странах араб-
ского Востока. Из Индии пришли три больших достижения:
позиционная десятичная система счисления, понятие отри-
цательного числа, понятие иррационального числа. Западная
Европа снова становится центром математического развития
только в XVI в., а в геометрии принципиально новые ша-
ги были сделаны только в XVII в., когда французский фи-
лософ и математик Р. Декарт (1596 — 1650) ввел в геометрию
метод координат, который позволил связать геометрию с ал-
геброй. В результате развилась аналитическая геометрия,
в которой геометрические фигуры задаются уравнениями.
Это позволило методы геометрии перенести в алгебру, а в ал-
гебре пользоваться наглядными геометрическими образами.
Исследования, связанные с устранением логических не-
достатков системы аксиом, предложен-
ной Евклидом, завершились к концу
XIX в., когда немецким математиком
Д. Гильбертом (1862 — 1943) (рис. 411)
была предложена первая полная аксио-
матика евклидовой геометрии. Важной
особенностью аксиоматики Гильберта
является то, что она представлена в фор-
ме, в которой наглядные представления
оставлены в стороне как несуществен-
ные для построения теории.
Рис. 410
Рис. 411
Правообладатель Народная асвета
Народная
асвета

26. 326
Точки и прямые в этом построении — это любые объек-
ты, а отношения между ними, обозначенные словами принад-
лежит, лежит между, конгруэнтно, — любые отношения,
о которых известно только то, что они удовлетворяют ука-
занным аксиомам. Неопределяемыми явно понятиями явля-
ются понятия: точка; прямая; плоскость; отношение при-
надлежности; отношение «лежать между»; отношение кон-
груэнтности (равенства). Они описываются аксиомами, раз-
деленными на 5 групп.
Аксиомы первой группы отношением лежит на (прохо-
дит через) связывают точку и прямую.
1.1. Есть только одна прямая, которой принадлежат две
данные точки.
1.2. На каждой прямой есть хотя бы две точки, и есть
хотя бы три точки, которые не лежат на одной прямой.
Аксиомы второй группы описывают отношение лежать
между, которое связывает три точки прямой. С использова-
нием этого отношения определяются понятия отрезка, луча,
угла, треугольника.
2.1. Если точка X лежит между точками A и B, то A, X,
B — различные точки одной прямой и точка X лежит меж-
ду точками B и A.
2.2. Если есть две точки A и B, то на прямой AB есть хотя
бы одна такая точка C, что B лежит между точками A и C.
2.3. Из трех точек прямой не более одной лежит между
двумя другими.
2.4. Если прямая не проходит ни через одну вершину тре-
угольника и пересекает одну из его сторон во внутренней точ-
ке, то она пересекает еще одну из двух других сторон.
Третья группа аксиом описывает отношение равенства для
отрезков и углов.
3.1. Каждый отрезок можно единственным способом от-
ложить на любом луче от его начала.
3.2. Если первый отрезок равен второму, а второй — тре-
тьему, то и первый отрезок равен третьему.
3.3. Суммы равных отрезков равны друг другу.
3.4. Каждый угол, меньший развернутого, можно единст-
венным способом отложить от данного луча в данную сторону.
3.5. Если две стороны и угол между ними одного тре-
угольника соответственно равны двум сторонам и углу дру-
гого треугольника, то такие треугольники равны.
Правообладатель Народная асвета
Народная
асвета

27. 327
Четвертая группа аксиом описывает свойство непрерыв-
ности прямой, которое соответствует нашему интуитивному
представлению о том, что на прямой нет просветов, дырок.
4.1. Для любых двух отрезков AB и CD на прямой AB от
точки A можно последовательно отложить отрезок CD столь-
ко раз, что получится отрезок AAn, больший отрезка AB
(рис. 412).
Рис. 412
4.2. Любая система вложенных отрезков [An; Bn] (рис. 413),
длины которых стремятся к нулю, когда n неограниченно уве-
личивается, имеет точку, принадлежащую всем этим отрезкам.
Рис. 413
Пятая группа аксиом состоит из одной аксиомы, которая
описывает отношение параллельности.
5.1. Через данную точку вне данной прямой можно про-
вести не более одной прямой, параллельной данной прямой.
Позже, в XX в., для евклидовой геометрии появились
и другие системы аксиом: немецкий математик Ф. Шур
(1856—1932) предложил аксиоматику, основанную на поня-
тии движения, русский математик В. Ф. Каган (1869—1953)
опубликовал аксиоматику, в основу которой положено поня-
тие расстояния, немецкий математик Г. Вейль (1885—1955)
предложил векторную аксиоматику. Такие системы аксиом
равносильны в том смысле, что, приняв одну из них, можно
так определить все понятия, используемые в других, что эти
понятия будут иметь все свойства, сформулированные в дру-
гих системах в качестве аксиом.
Правообладатель Народная асвета
Народная
асвета

28. 328
Отметим, что при построении курса геометрии могут ис-
пользоваться различные варианты одной и той же аксиомати-
ки. Например, вместо аксиомы параллельных можно принять
в качестве аксиомы утверждение о сумме углов треугольника,
так как эти утверждения равносильны, т. е. истинность одно-
го из них влечет за собой истинность другого, понятно, при
истинности остальных аксиом. Эти различные варианты ак-
сиоматики дают одинаковые теории, т. е. с их помощью мож-
но доказать одни и те же теоремы.
? 1. Назовите основные понятия аксиоматической теории евклидовой
геометрии.
2. Приведите примеры аксиом, описывающих отношение принадлеж-
ности.
3. Приведите примеры аксиом, описывающих отношение лежать
между.
4. Приведите примеры аксиом, описывающих отношение равенства.
5. Сформулируйте аксиому параллельности.
1186. Докажите, что если в треугольнике ABC можно вы-
брать такую точку M, что AM = AB, то AB AC.
1187. В выпуклом четырехугольнике ABCD диагональ AC
равна стороне AD. Докажите, что сторона BC меньше диа-
гонали BD.
1188. Докажите, что два треугольника равны, если они
имеют пары равных углов при одной стороне и равные вы-
соты, проведенные к этим сторонам.
1189. Докажите, что биссектриса внешнего угла паралле-
лограмма вместе с продолжениями его сторон, не проходящих
через эту вершину, образуют равнобедренный треугольник.
1190. Докажите, что если вершины одного параллелограм-
ма находятся по одной на сторонах другого параллелограмма,
то эти параллелограммы имеют общий центр.
1191. Докажите, что биссектрисы углов, прилежащих к
боковой стороне трапеции, пересекаются на средней линии
под прямым углом.
1192. Докажите, что сумма диаметров окружностей, опи-
санной около прямоугольного треугольника и вписанной в не-
го, равна сумме катетов.
1193. Докажите, что окружность, которая проходит че-
рез ортоцентр треугольника и две его вершины, равна окруж-
ности, описанной около этого треугольника.
Правообладатель Народная асвета
Народная
асвета

29. 329
1194. Докажите, что высоты треугольника являются бис-
сектрисами углов треугольника, который определяется осно-
ваниями этих высот.
1195. Докажите, что диаметр окружности, вписанной в
равнобедренную трапецию, является средним геометриче-
ским оснований трапеции.
1196. Две окружности пересекаются в точках A и B. Через
точку A проведены хорды AC и AD, которые касаются данных
окружностей. Докажите, что AC2
BD = AD2
BC.
1197. Через точку A вне окружности проведены прямые,
касающиеся окружности в точках B и C. Докажите, что центр
окружности, вписанной в треугольник ABC, лежит на данной
окружности.
1198. Около правильного треугольника ABC описана
окружность, и на дуге BC взята произвольная точка M. До-
кажите, что AM = BM + CM.
1199. Точки касания вписанной в треугольник окружно-
сти разбивают его стороны на отрезки длинами m, n, k. До-
кажите, что площадь S треугольника выражается формулой
S mnk m n k= ( ).+ +
44444
1200. Две стороны треугольника равны 25 см и 30 см,
а угол против одной из них в два раза больше угла против
другой. Найдите третью сторону треугольника и радиусы
окружностей, вписанной в этот треугольник и описанной
около него.
1201. Угол A в треугольнике ABC в два раза больше
угла B. Найдите сторону BC, учитывая, что AB = c и AC = b.
1202. Две стороны треугольника равны 12 см и 24 см, а
угол между ними — 120°. Найдите биссектрису, проведенную
к третьей стороне треугольника.
1203. Две стороны треугольника равны 20 см и 45 см, а
биссектриса, проходящая между ними, — 24 см. Найдите от-
резки, на которые биссектриса разбивает третью сторону тре-
угольника.
1204. Две стороны треугольника равны 10 см и 17 см. Най-
дите третью сторону треугольника, учитывая, что он вписан
в окружность с диаметром 21,25 см.
Правообладатель Народная асвета
Народная
асвета

30. 330
1205. Найдите площадь треугольника, учитывая, что две
его стороны вместе составляют 30 см, а высоты, проведенные
к ним, равны 8 см и 12 см.
1206. Две стороны треугольника равны 20 см и 28 см, а
угол против меньшей из них — 45°. Найдите площадь тре-
угольника.
1207. Две стороны треугольника равны 25 см и 30 см, а
площадь — 300 см2
. Найдите третью сторону треугольника.
1208. Найдите площадь треугольника, учитывая, что две
его стороны равны 27 см и 29 см, а медиана, проведенная к
третьей, — 26 см.
1209. Стороны треугольника равны 65 см, 70 см и 75 см.
Через основания высот, проведенных к двум большим сторо-
нам, проходит прямая. Найдите площади частей, на которые
эта прямая разбивает треугольник.
1210. Стороны AB, BC, CD, DA четырехугольника ABCD и
его диагональ AC соответственно равны 26 см, 30 см, 17 см,
25 см и 28 см. Найдите площадь четырехугольника и его вто-
рую диагональ.
1211. Углы при большем основании трапеции равны 30°,
а диагонали являются их биссектрисами. Найдите периметр
трапеции, учитывая, что ее площадь равна 24 см2
.
1212. Высота трапеции равна 12 см, а ее диагонали —
20 см и 15 см. Найдите площадь этой трапеции.
1213. На стороне AB треугольника ABC отмечена точка D,
делящая сторону в отношении m : n, а на стороне BC — точ-
ки E и F, делящие эту сторону в отношении p : q : r. Опре-
делите, в каком отношении площадь треугольника делится
прямыми DE и DF.
1214. Прямыми, параллельными основанию, площадь тре-
угольника разделена в отношении 9 : 55 : 161, если считать
от вершины. Определите, в каком отношении эти прямые де-
лят стороны.
1215. Основания трапеции относятся как m : n. Опре-
делите отношение площадей частей, на которые трапеция
делится ее диагоналями.
1216. Найдите периметр равнобедренной трапеции, осно-
вания и боковая сторона которой относятся как 10 : 4 : 5, а
площадь равна 112 м2
.
Правообладатель Народная асвета
Народная
асвета

31. 331
1217. Отрезки, соединяющие с вершинами треугольника
центр вписанной в него окружности, разделяют треугольник
на части с площадями 30 см2
, 28 см2
, 26 см2
. Найдите сто-
роны треугольника.
1218. Найдите радиус окружности, описанной около рав-
нобедренной трапеции с основаниями 2 см и 8 см.
1219. Найдите стороны треугольника, учитывая, что рас-
стояния от них до точки пересечения медиан относятся как
2 : 3 : 4, а периметр треугольника равен 26 м.
1220. Две вершины квадрата расположены на хорде, стя-
гивающей дугу в 120°, а две другие — на этой дуге. Найдите
радиус соответствующего круга, учитывая, что сторона квад-
рата равна 3 м.
1221. На боковой стороне равнобедренного треугольника
как на диаметре построена окружность. Найдите отрезки, на
которые эта окружность делит боковую сторону и основание,
учитывая, что они равны соответственно 9 см и 6 см.
1222. Имеются окружности с радиусами 5 см и 20 см, касаю-
щиеся внешним образом, к которым проведены общие внешние
касательные. Найдите расстояния между точками касания.
1223. Диагональ прямоугольника, одна сторона которого
лежит на основании равнобедренного треугольника, а проти-
воположная оканчивается на его боковых сторонах, перпен-
дикулярна боковой стороне. Найдите стороны прямоугольни-
ка, учитывая, что основание треугольника и проведенная к
нему высота равны 6 м.
1224. Диагональ и отрезки, соединяющие середины про-
тивоположных сторон четырехугольника, соответственно
равны 12 см, 7 см и 11 см. Найдите другую диагональ че-
тырехугольника.
1225. Диагональ и отрезки, соединяющие середины проти-
воположных сторон четырехугольника, соответственно равны
10 см, 6 см и 8 см. Найдите площадь четырехугольника.
1226. Окружность с радиусом 6 см внешним образом ка-
сается двух окружностей с радиусами 3 см, при этом центры
всех окружностей лежат на одной прямой. Найдите радиус
окружности, которая касается всех трех окружностей.
1227. Есть ромб со стороной a и углом α. Найдите радиус
окружности, которая проходит через две его смежные верши-
ны и касается прямой, проходящей через две другие вершины.
Правообладатель Народная асвета
Народная
асвета

32. 332
1228. Окружности с радиусами 8 и 18 касаются внешним
образом и имеют общую касательную. Третья окружность ка-
сается этих окружностей и их касательной. Найдите ее радиус.
1229. В равнобедренную трапецию вписана окружность
с радиусом 18. Точкой касания боковая сторона делится
на части, разность которых равна 15. Найдите площадь
трапеции.
1230. На плоскости отмечены такие точки E, G, I и K, что
∠EGK = 34°, ∠EKI = 84°, ∠IGK = 62°. Найдите величину уг-
ла IEK.
1231. На окружности с радиусом r выбраны три точки,
которые разделяют окружность на три дуги в отношении
3 : 4 : 5. Найдите площадь треугольника, образованного ка-
сательными к окружности, проведенными через точки де-
ления.
1232. Около окружности описана равнобедренная трапе-
ция с боковой стороной b, одно основание которой равно a.
Найдите площадь трапеции.
1233. Трапеция разделена на три части двумя прямыми,
параллельными основаниям трапеции и делящими каждую
из боковых сторон на три доли. Найдите площадь средней ча-
сти, учитывая, что площади крайних равны P и Q.
1234. Стороны AB и BC трапеции ABCD соответственно
равны k и l, причем k ≠ l. Определите, что пересекает бис-
сектриса угла A: основание BC или боковую сторону CD.
1235. Найдите длину отрезка, который параллелен осно-
ваниям трапеции, соединяет точки на боковых сторонах и
проходит через точку пересечения диагоналей, учитывая, что
основания трапеции равны a и b.
1236. Отношение оснований равнобедренной трапеции,
описанной около окружности, равно k. Найдите косинус уг-
ла при основании трапеции.
1237. Основания MN и OP трапеции MNOP соответствен-
но равны a и b. Найдите площадь трапеции, учитывая, что
диагонали трапеции являются биссектрисами углов PMN и
MNO.
1238. Средняя линия равнобедренной трапеции равна a,
а диагонали взаимно перпендикулярны. Найдите ее пло-
щадь.
Правообладатель Народная асвета
Народная
асвета

33. 333
1239. Площадь равнобедренной трапеции, описанной око-
ло круга, равна S, а ее высота в два раза меньше боковой сто-
роны. Найдите радиус круга.
1240. Площади треугольников, ограниченных отрезками
диагоналей трапеции и ее основаниями, равны S1 и S2. Най-
дите площадь трапеции.
1241. Запишите многочленом стандартного вида выра-
жение:
а) (n + m)3
− (n − m)3
;
б) (q4
− q2
c2
+ c4
)(q2
+ c2
);
в) (2a3
− a2
+ 4a − 3)(a2
− a + 5);
г) (3l − 5k + 8j)(2l − 3k) + (2l − 5k + 6j)(3k − 2l);
д) (2h − 3g + 4f)(5h + 4g) − (3h − 2g)(3g − 2h − 4f);
е) (s3
− 3s2
d + 3sd2
− d3
)(s2
− 2sd + d2
).
1242. Разложите на множители выражение:
а) qh − q + h − 1; д) 10m2
+ 21gy − 14mg − 15my;
б) 18cs − 24zs − 9c + 12z; е) 8j2
h − 8j2
f + 6f2
h − 6f3
;
в) 3er − 4sd − 4ed + 3sr; ж) b2
m3
− bmn2
y + n3
y2
− bm2
ny;
г) 30z2
− 18zp − 35zq + 21qp; з) lk2
− sk2
+ sk − lk + l − s.
1243. Упростите выражение:
а)
q l
q q l l
2 2
2 2
−
− − −
; ж)
j j
j j
2
2
5 6
4 4
+ +
+ +
;
б)
5 5
5
3 2 2 3
2
e e r er r
er r
+ + +
+
; з)
h h
h h
2
2
3 2
6 5
+ +
+ +
;
в)
t
t t
3
2
1
6 12 6
+
+ +
; и)
g g
g g
2
2
7 12
6 9
− +
− +
;
г)
( )
;
y e
y e ye y
+
+ +
3
2 2 3
2
к)
f f
f f
2
2
2 1
8 7
+ +
+ +
;
д)
3
3 3
2 2
3 2 2 3
n p np
n np n p p
−
− − +
; л)
2
2
2 2 2
2 2 2
ds d s z
d z s dz
− − +
+ − +
;
е)
l k lk
l k lk l k
2 2
3 3
3
+
+ + +( )
; м)
c с a ca
a c
3 2 2
3 3
− +
+
.
Правообладатель Народная асвета
Народная
асвета

34. 334
1244. Сократите дробь:
а)
1
2
2
3 2
−
+ +
b
b b b
; г)
qs q
q s
2 3
2
16
4
−
+( )
; ж)
d p
d d p dp
3 3
3 2 2
2
+
+ +
;
б)
n nm m
n n m
2 2
6 3 3
+ +
−
; д)
e r e r er
r e
3 2 2 3
2 2
2+ +
−
; з)
k kl l
k l l
2 2
3 4
2
2 2
+ +
+
.
в)
a a
a a
2
3
6 9
9
− +
−
; е)
2
3 122 2
t y
y t
+
−
;
1245. Упростите выражение:
а) 8
2 3q −
+ 5
3 2− q
−
3 4
2 32
q
q q
−
− −
;
б) h
j
−
( )h j g
j
2 2
2
−
+
h h j g
j j hg
( )
( )
;
2 2 2
2
−
+
в)
e r
r
+
− 2e
e r+
+
e e r
r re
3 2
3 2
−
−
;
г)
t a
ta
−
− t
a at2
+
+ a
ta t+ 2
;
д) 1
( )( )s d f d− +
+ 1
( )( )
;
d s f s− +
е) g
g h g j( )( )− −
+ h
h g h j( )( )− −
+
j
j g j h( )( )
.
− −
1246. Упростите выражение:
а)
a b
b c ab
− −
− −
−
−
1 1
1 1
( )
;
б)
( )( )
( )
;
xy x y x y
x y x y xy x y
− − − −
− − − −
+ + −
+ − +
1 1 1 1 2
2 2 2 2 1 1
1
в)
( )
(( ) )
( )
(( ) )
;
1
1
1
1
1 1
1 1 1
1 1
1 1 1
+ +
− −
−
+ +
− −
− −
− − −
− −
− − −
ab a
a b b
a b b
ab a
г)
1 1
1 1
1 2
1 1 2
− + −
− + −
− −
− −
( ( ) )
( ( ( ) ) )
.
a a
a a
1247. Решите систему:
а)
x x
x
2
3 4
3 2
= +⎧
⎨
⎪
⎩⎪
,
;
в)
− = −
−
⎧
⎨
⎪
⎩⎪
2 3 5
1 2
2
x x
x
,
;
б)
x x
x
2
2 15
3 1
+ =
−
⎧
⎨
⎪
⎩⎪
,
;
г)
( ) ,
.
2 3 9
2 2
x x
x
− =
−
⎧
⎨
⎩
Правообладатель Народная асвета
Народная
асвета

35. 335
1248. Решите систему уравнений:
а)
( )( ) ,
( )( ) ;
h j h
h j j
+ − =
+ − =
⎧
⎨
⎩
8 10
5 20
в)
z c z c
z c c c
2 2
2
5 3 22 0
3 2 3 2
− − − + =
− − = − +
⎧
⎨
⎪
⎩⎪
,
( )( ) ;
б)
2 3 5 5 0
2 1 0
2
k kl l
k l
− + − =
− − =
⎧
⎨
⎪
⎩⎪
,
( )( ) ;
г)
( ) ( ) ,
( ) ( ) .
b n b n
b n b n
+ − + =
− − − =
⎧
⎨
⎪
⎩⎪
2
2
4 45
2 3
1249. Решите систему уравнений:
а)
q qe
e qe
2
2
7
9
+ =
+ =
⎧
⎨
⎪
⎩⎪
,
;
в)
d
d
h
h
d
d
h
h
− −
+ −
+ =
+ =
⎧
⎨
⎪
⎩
⎪
1 2
1 1
1
3
,
;
б)
3
1
10
1
1
y
p
p
y
y
p y
−
+
=
=
⎧
⎨
⎪
⎩
⎪
,
;
г)
l k
k
l k
l
kl k l
− +
+ =
− + =
⎧
⎨
⎪
⎩⎪
2 5
2 6
, ,
.
1250. Постройте график функции U = −y2
− 4y + 5 и, ис-
пользуя его, решите неравенство:
а) −y2
− 4y + 5 0; в) −y2
− 4y + 5 0;
б) −y2
− 4y + 5 0; г) −y2
− 4y + 5 0.
1251. Решите неравенство:
а) (a − 5)2
(a2
− 81) 0; е) (f − 3)(f2
− 121) 0;
б) (b + 6)3
(b2
− 100) 0; ж) (g3
− 1)(g2
− 4) 0;
в) (c + 8)3
(c2
− 169) 0; з) (h3
+ 64)(h2
− 9) 0;
г) (d2
− 1)(d + 3) 0; и) (i3
+ 125)(i + 6) 0.
д) (e2
− 49)(e − 5) 0;
1252. Решите неравенство:
а)
p
p
+
−
2
2 3
1; е)
v
v
+
−
1
1
+ 2
v
v
− 1
;
б)
5 3
4
q
q
−
−
2; ж) 3 −
2 17
5
h
h
−
−
h
h
−
+
5
2
;
в)
10
5 2
−
+
s
s
1
2
; з) 1
1w +
+ 2
3w +
3
2w +
;
г)
t t
t t
2
2
5 6
5 6
− +
+ +
0; и) 3
1x +
+ 7
2x +
6
1x −
;
д) 2 −
w
w
−
−
3
2
w
w
−
−
2
1
; к) 3
1l −
+ 7
2l −
6
1l +
.
Правообладатель Народная асвета
Народная
асвета

36. 336
1253. Решите систему неравенств:
а)
x x
x x
2
2
4 5 0
2 4 3 0
− +
− −
⎧
⎨
⎪
⎩⎪
,
;
в)
− − +
+ −
⎧
⎨
⎪
⎩⎪
x x
x x
2
2
2 8 0
3 4 0
,
;
б)
x x
x x
2
2
10 24 0
2 11 5 0
− +
− +
⎧
⎨
⎪
⎩⎪
,
;
г)
x x
x x
2
2
9 6
4 9 12
+ −
+
⎧
⎨
⎪
⎩⎪
,
.
1254. Определите, при каких значениях аргумента зна-
чение функции равно 2:
а) y x
x
=
+ −
5
2 1 5
; в) y
x x
= +
+ − −
1
2 2
1;
б) y
x x
=
− − +
5
2 2 3
; г) y х
x x
= −
− −
4
3 3 1
2
+
.
1255. Найдите сумму квадратов корней уравнения:
а) x2
+ 2⎜x⎟ − 1 = 0; в) x2
− 3⎜x⎟ + 1 = 0;
б) x2
− 3⎜x⎟ − 1 = 0; г) x2
+ 6⎜x⎟ − 1 = 0.
1256. Найдите сумму корней уравнения:
а) (x − 4)(x − 5)(x − 6)(x − 7) = 1680;
б) x(x + 3)(x + 5)(x + 8) = 100;
в) (x + 6)(x + 3)(x − 1)(x − 2) = 12x2
;
г) (x − 4)(x + 5)(x + 10)(x − 2) = 18x2
.
1257. Составьте таблицы значений для функций
y = x2
+ x − 2 и y = –(x2
+ x − 2) на промежутке [–4; 4] и построй-
те графики этих функций. Сравните их и сделайте вывод.
1258. Докажите, что графики функций y = –f(x) и y = f(x)
симметричны относительно оси Ox.
1259. Составьте таблицы значений для функций
y = x2
+ x − 2 и y = ⎜x2
+ x − 2⎟ на промежутке [–4; 4] и построй-
те графики этих функций. Сравните их и сделайте вывод.
1260. Докажите, что графики функций y = ⎜f(x)⎟ и y = f(x)
совпадают при тех значениях x, при которых f(x) 0, и сим-
метричны относительно оси Ox при тех значениях x, при ко-
торых f(x) 0.
1261. Составьте таблицы значений для функций
y = ⎜x⎟2
+ ⎜x⎟ − 2 и y = x2
+ x − 2 на промежутке [–4; 4] и по-
стройте графики этих функций. Сравните их и сделайте вывод.
Правообладатель Народная асвета
Народная
асвета

37. 337
1262. Докажите, что график функции y = f(⎜x⎟) симметри-
чен относительно оси Oy и совпадает с графиком функции
y = f(x) при x 0.
1263. Составьте таблицы значений для функций y = x3
и
y = x3
+ 2 на промежутке [–3; 3] и постройте графики этих
функций. Сравните их и сделайте вывод.
1264. Докажите, что график функции y = f(x) + a получает-
ся переносом графика функции y = f(x) вдоль оси Oy на a еди-
ниц вверх, если a 0, и на ⎜a⎟ единиц вниз, если a 0.
1265. Составьте таблицы значений для функций y x= и
y x= + 2 для чисел, меньших 10, и постройте графики этих
функций. Сравните их и сделайте вывод.
1266. Докажите, что график функции y = f(x + a) получает-
ся переносом графика функции y = f(x) вдоль оси Ox на a еди-
ниц влево, если a 0, и на ⎜a⎟ единиц вправо, если a 0.
1267. Составьте таблицы значений для функций y x= и
y x= − для чисел, меньших 10 по модулю, и постройте гра-
фики этих функций. Сравните их и сделайте вывод.
1268. Докажите, что график функции y = f(–x) получает-
ся симметричным отражением графика функции y = f(x) от-
носительно оси Oy.
1269. Составьте таблицы значений для функций y x=
и y x= 2 на промежутке [0; 9] и постройте графики этих
функций. Сравните их и сделайте вывод.
1270. Докажите, что график функции y = kf(x) получается
из графика функции y = f(x) растяжением его вдоль оси Oy в
k раз, если k 1, и сжатием в 1
k
раз, если 0 k 1.
1271. Составьте таблицы значений для функций y x=
и y x= 2 на промежутке [0; 9] и постройте графики этих
функций. Сравните их и сделайте вывод.
1272. Докажите, что график функции y = f(kx) получается
из графика функции y = f(x) сжатием к оси Oy в k раз, если
k 1, и растяжением в 1
k
раз, если 0 k 1.
1273. Из населенного пункта A в населенный пункт B, рас-
стояние между которыми равно 234 км, выехал один мотоцик-
лист. Другой мотоциклист выехал из пункта B со скоростью
Правообладатель Народная асвета
Народная
асвета

38. 338
на 12 км больше через час после этого и встретил первого,
проехав 108 км. Найдите скорости мотоциклистов.
1274. Мастер может выполнить заказ на четыре дня бы-
стрее, чем ученик. Определите, за какое время каждый из них
может выполнить заказ, учитывая, что за 24 дня при совмест-
ной работе они могут выполнить заказ, в пять раз больший.
1275. Часы спешат, но в некоторый момент показывают
на 3 мин меньше, чем следует. Если бы они показывали на
1 мин меньше, но спешили бы еще на 1 мин в сутки, то вер-
ное время они показали бы на сутки раньше, чем покажут на
самом деле. На сколько минут в сутки спешат эти часы?
1276. Две бригады, работая вместе, могут выполнить всю
работу за 18 дней. Если бы сначала первая бригада выполнила
2
3
всей работы, а затем вторая — оставшуюся часть, то вся
работа была бы выполнена за 40 дней. Определите, за сколь-
ко дней каждая бригада, работая отдельно, может выполнить
всю работу.
1277. По наклонной плоскости длиной 6 м катятся два ци-
линдра, длины окружностей их оснований равны 3 дм и 2 дм.
Определите, на сколько надо увеличить длину окружности
того и другого цилиндров, чтобы первый из них сделал
на 3 оборота больше, чем второй.
1278. На обработку одной детали первый рабочий затрачи-
вает на 7 мин меньше второго. Определите, сколько деталей
каждый из них обработает за 4 ч, учитывая, что первый рабо-
чий за это время обработает на 96 деталей больше второго.
1279. Из населенного пункта A в пункт B вышел один пеше-
ход, а через полчаса вслед за ним — другой пешеход, который
шел со скоростью 4 км/ч, догнал первого и сразу же пошел
обратно. Найдите скорость первого пешехода, учитывая, что
расстояние между населенными пунктами составляет 10 1
2
км
и второй пешеход вернулся в пункт A в тот момент, когда пер-
вый пришел в пункт B.
1280. При напряжении в 10 В сила тока в одной цепи на
1 А больше силы тока в другой цепи при напряжении в ней
в 6 В. Если уменьшить сопротивление каждой цепи на 1
2
Ом,
то ток в первой цепи станет на 2
3
А больше, чем во второй.
Найдите силу тока в каждой цепи.
Правообладатель Народная асвета
Народная
асвета

39. 1281. Туристы сначала ехали 1,5 ч на машине, а затем
3 ч поездом. Найдите путь, который преодолели туристы,
учитывая, что скорость поезда была в 1,5 раза меньше ско-
рости машины, а средняя скорость на всем пути оказалась
равной 70 км/ч.
1282. Есть два цилиндра с высотами 10 см и 15 см, пло-
щади оснований которых относятся как 3 : 4. Сумма объемов
этих цилиндров равна 1800 см3
. Найдите их объемы, учиты-
вая, что объем цилиндра равен произведению площади его
основания на высоту.
* * *
1283. Докажите, что для любого целого числа m найдутся
такие целые числа n и k, что m
n k
n k
=
− +
−
2 1
2
.
1284. Есть три последовательности из натуральных
чисел:
a1, a2, a3, …, an, …;
b1, b2, b3, …, bn, …;
c1, c2, c3, …, cn, ….
Докажите, что найдутся такие номера k и m, что ak am,
bk bm, ck cm.
1285. Точки K и N выбраны на окружностях, которые пе-
ресекаются в точках A и B, так, что прямые AK и AN яв-
ляются касательными к этим окружностям в точке A, а точ-
ка M симметрична точке A относительно точки B. Докажите,
что через точки A, K, M и N можно провести окружность.
Правообладатель Народная асвета
Народная
асвета

40. 340
АРИФМЕТИКА
Арифметика — та часть школьной математики, в кото-
рой изучаются числа, действия над числами, числовые вы-
ражения.
Натуральные числа
Для именования натуральных чисел в десятичной позици-
онной системе счисления пользуются знаками
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
которые называют цифрами.
Любая последовательность цифр, которая не начинается
цифрой 0, представляет натуральное число. Все натуральные
числа вместе составляют множество натуральных чисел, ко-
торое обозначают N.
Над натуральными числами всегда выполнимы действия
сложения, умножения и возведения в степень, т. е. каждое
из этих действий, примененное к натуральным числам, име-
ет результатом натуральное число.
Прибавить к натуральному числу a натуральное число b
означает к натуральному числу a присчитать последовательно
b единиц:
a + b =
опр
( (( ) ) ).K K
1 244 344
a
b
+ + + +1 1 1
единиц
Если a + b = c, то числа а и b называют слагаемыми, а чис-
ло c — суммой. Выражение a + b также называют суммой.
Умножить натуральное число a на натуральное число b
означает натуральное число a взять слагаемым b раз:
a b =
опр
(( (( ) ) ) ).K K
1 2444 3444
a a a a
b
+ + + +
слагаемых
Если a b = c, то числа а и b называют множителями, а чи-
сло c — произведением. Первый множитель a называют еще
множимым. Выражение a b также называют произведением.
Действием, обратным сложению, является вычитание. Из
натурального числа a вычесть натуральное число b означает
Правообладатель Народная асвета
Народная
асвета

41. 341
найти такое натуральное число c, сумма которого с числом b
равна числу a:
a − b = c ≡
опр
c + b = a.
Если a − b = c, то число а называют уменьшаемым, число
b — вычитаемым, а число c — разностью. Выражение a − b
также называют разностью.
Действием, обратным умножению, является деление. На-
туральное число a разделить на натуральное число b означает
найти такое натуральное число c, произведение которого и
числа b равно числу a:
a : b = c ≡
опр
c b = a.
Если a : b = c, то число а называют делимым, число b — де-
лителем, а число c — частным. Выражение a : b также на-
зывают частным.
Основное свойство частного: частное не изменится, если
делимое и делитель умножить или разделить на одно и то же
число.
Натуральное число a возвести в натуральную степень n
означает натуральное число a взять множителем n раз:
an
=
опр
(( (( ) ) ) ).K K
1 2444 3444
a a a a
n множителей
Если an
= c, то число а называют основанием степени, чис-
ло n — показателем степени, а число c — степенью. Вы-
ражение an
также называют степенью.
Вторая степень числа называется еще квадратом числа,
третья — кубом числа.
Действием, обратным возведению в квадрат, является
извлечение квадратного корня. Извлечь квадратный корень
из числа a означает найти такое натуральное число c, что его
вторая степень равна числу a:
a = c ≡
опр
c2
= a.
Если a = c, то число а называют подкоренным числом,
а число c — квадратным корнем. Выражение a также на-
зывают квадратным корнем.
Обратные действия — вычитание, деление и извлечение
квадратного корня — не всегда выполнимы на множестве
натуральных чисел. Например, нет натурального числа, ко-
Правообладатель Народная асвета
Народная
асвета

42. 342
торое является значением разности 3 – 7, или которое яв-
ляется значением частного 3 : 7, или которое является зна-
чением корня 2.
Если при делении натурального числа a на натуральное
число b получается натуральное число c, то говорят, что на-
туральное число a делится (нацело) на натуральное число b,
или что натуральное число a кратно натуральному числу b,
или что число b есть делитель числа a.
Рассматривается еще и действие деления с остатком од-
ного натурального числа на другое. Натуральное число a раз-
делить с остатком на натуральное число b означает найти
такие неотрицательные целые числа p и q, что произведение
числа p и числа b, будучи сложенным с числом q, равно
числу a и при этом число q меньше числа b:
a : b = p (ост. q) ≡
опр
p b + q = a и q b.
Деление с остатком всегда выполнимо на множестве на-
туральных чисел.
Число, которое делится на 2, называется четным числом,
а которое не делится — нечетным числом.
Цифры 0, 2, 4, 6, 8 называются четными, а цифры 1, 3,
5, 7, 9 — нечетными.
Свойства числа, которое делится Признак делимости числа
Если число делится на 10, то оно
оканчивается цифрой 0
Если число оканчивается цифрой 0,
то оно делится на 10
Четное число оканчивается четной
цифрой
Если число оканчивается четной
цифрой, то оно делится на 2
Если число делится на 5, то оно окан-
чивается цифрой 0 или цифрой 5
Если число оканчивается цифрой 0
или цифрой 5, то оно делится на 5
Если число делится на 3, то сумма
его цифр делится на 3
Если сумма цифр числа делится на
3, то оно делится на 3
Если число делится на 9, то сумма
его цифр делится на 9
Если сумма цифр числа делится на
9, то оно делится на 9
Число, которое имеет точно два натуральных делителя,
называется простым числом.
Число, имеющее более двух натуральных делителей, на-
зывается составным числом.
Каждое натуральное число однозначно раскладывается в
произведение простых множителей, если не обращать вни-
мания на порядок их записи. Если множитель входит в раз-
ложение некоторого числа на простые множители несколько
Правообладатель Народная асвета
Народная
асвета

43. 343
раз, то количество этих вхождений называется кратностью
множителя.
Наибольшее из чисел, на которые делятся данные числа,
называется наибольшим общим делителем (НОД) этих чисел.
Наименьшее из чисел, которое делится на все данные числа,
называется наименьшим общим кратным (НОК) этих чисел.
Чтобы найти НОД нескольких натуральных чисел, мож-
но разложить их на простые множители, выбрать общие мно-
жители с учетом их кратностей и затем выбранные числа пе-
ремножить.
Чтобы найти НОК нескольких натуральных чисел, можно
разложить их на простые множители, выбрать те множители,
которые входят в разложение хотя бы одного из данных чи-
сел с учетом их наибольших кратностей, и затем выбранные
числа перемножить.
Если НОД двух чисел равен единице, то такие числа на-
зываются взаимно простыми.
Неотрицательные рациональные числа
Долей называется одна из равных частей, на которые раз-
делено целое.
Обыкновенной дробью называется любое количество долей.
Обыкновенная дробь, состоящая из n-х долей, которых
есть m, записывается как m
n
:
m
n
=
опр
1 1 1
n n n
m
+ + +K
1 244 344
долей
= 1
n
m.
В записи m
n
число m называется числителем дроби,
число n — знаменателем дроби.
Черта дроби и знак деления взаимозаменяемы:
m
n
= m : n.
Если числитель дроби меньше знаменателя, то дробь на-
зывается правильной.
Если числитель дроби больше знаменателя или равен ему,
то дробь называется неправильной.
Если в неправильной дроби, например 15
4
, выделить целую
и дробную части и записать их одна за другой, то полученную
запись 3 3
4
называют смешанной дробью:
3 3
4
=
опр
3 + 3
4
.
Правообладатель Народная асвета
Народная
асвета

44. 344
Чтобы неправильную дробь представить смешанной дро-
бью, можно числитель неправильной дроби разделить с остат-
ком на ее знаменатель.
Чтобы смешанную дробь представить неправильной дро-
бью, можно целую часть смешанной дроби умножить на зна-
менатель ее дробной части, к полученному произведению при-
бавить числитель дробной части и полученную сумму записать
числителем неправильной дроби, оставив прежний знаменатель.
Основное свойство дроби: величина дроби не изменится,
если ее числитель и знаменатель умножить или разделить на
одно и то же число.
Умножение числителя и знаменателя обыкновенной дроби
на одно и то же натуральное число называется приведением
дроби к новому знаменателю.
Деление числителя и знаменателя обыкновенной дроби на
одно и то же натуральное число называется сокращением дроби.
Сокращением дробь можно свести к простейшей дроби с
взаимно простыми числителем и знаменателем, которая на-
зывается несократимой дробью.
Есть бесконечно много дробей, равных друг другу:
3
5
= 6
10
= 9
15
= 12
20
= … .
Каждая из равных друг другу дробей является предста-
вителем определенного рационального числа. Среди пред-
ставителей того или иного рационального числа есть пред-
ставитель с наименьшим знаменателем, который является не-
сократимой дробью.
Каждое натуральное число имеет бесконечно много пред-
ставителей:
5 = 5
1
= 10
2
= 15
3
= 20
4
= 25
5
= … .
Дробями представляются и числа, не являющиеся нату-
ральными. Такие числа называют дробными числами.
Дробные числа вместе с натуральными числами и чис-
лом 0 составляют множество неотрицательных рациональных
чисел, которое обозначается Q0.
Чтобы привести дроби к общему знаменателю, можно в
качестве общего знаменателя взять НОК знаменателей дан-
ных дробей и умножить числитель и знаменатель каждой из
дробей на частное от деления общего знаменателя на знамена-
тель соответствующей дроби. Частное от деления общего зна-
менателя данных дробей на знаменатель той или иной дроби
называется дополнительным множителем.
Правообладатель Народная асвета
Народная
асвета

45. 345
Чтобы сложить две дроби с одинаковыми знаменателями, до-
статочно сложить их числители, оставив знаменатель прежним:
m
k
+ n
k
=
m n
k
+
.
Чтобы сложить две дроби с разными знаменателями, нуж-
но предварительно привести их к общему знаменателю.
Чтобы из одной дроби вычесть другую дробь со знамена-
телем, равным знаменателю первой дроби, достаточно из
числителя первой дроби вычесть числитель второй дроби,
оставив знаменатель прежним:
m
k
− n
k
=
m n
k
−
.
Чтобы выполнить вычитание дробей с разными знаменателя-
ми, нужно предварительно привести их к общему знаменателю.
Чтобы умножить дробь на натуральное число, можно
умножить на это число числитель дроби, оставив знаменатель
прежним, или разделить на это число знаменатель, оставив
прежним числитель:
m
n
k =
m k
n
= m
n k:
.
Чтобы разделить дробь на натуральное число, можно раз-
делить на это число числитель дроби, оставив знаменатель
прежним, или умножить на это число знаменатель, оставив
прежним числитель:
m
n
: k =
m k
n
:
= m
n k
.
Чтобы умножить дробь на дробь, достаточно перемножить
в отдельности их числители и их знаменатели, записав произ-
ведение числителей в числитель дроби-произведения, а произ-
ведение знаменателей — в знаменатель дроби-произведения:
k
l
m
n
= km
nl
.
Два числа, произведение которых равно единице, называ-
ют взаимно обратными.
Чтобы одну дробь разделить на другую, достаточно первую
дробь умножить на дробь, обратную другой:
k
l
: m
n
= k
l
n
m
= kn
lm
.
Обыкновенная дробь, знаменателем которой является раз-
рядная единица, называется десятичной дробью.
Обыкновенную дробь можно превратить в десятичную
делением числителя на знаменатель. При этом полученная
Правообладатель Народная асвета
Народная
асвета

46. 346
десятичная дробь будет конечной или бесконечной периоди-
ческой без допериода или с допериодом:
7
40
= 0,175; 36
37
= 0,(972); 97
165
= 0,5(87).
Чтобы конечную десятичную дробь преобразовать в обык-
новенную, можно записать дробь с числителем, равным дроб-
ной части десятичной дроби, и знаменателем, равным раз-
рядной единице со столькими нулями, сколько цифр в дроб-
ной части десятичной дроби, и затем сократить полученную
обыкновенную дробь:
0,175 = 175
1000
= 7
40
.
Чтобы бесконечную периодическую десятичную дробь
без допериода преобразовать в обыкновенную, можно запи-
сать обыкновенную дробь, числитель которой равен периоду,
а знаменатель — числу, записанному столькими девятками,
сколько цифр в периоде, и затем сократить полученную обык-
новенную дробь:
0,(972) = 972
999
= 108
111
= 36
37
.
Чтобы бесконечную периодическую десятичную дробь
с допериодом преобразовать в обыкновенную, можно запи-
сать обыкновенную дробь, числитель которой равен разности
между числом, записанным цифрами от десятичной запятой
до конца первого периода, и числом, записанным цифрами
допериода, а знаменатель — числу, записанному столькими
девятками, сколько цифр в периоде, и столькими нулями,
сколько цифр в допериоде:
0,5(87) =
587 5
990
−
= 582
990
= 97
165
.
Сотая доля называется процентом, а тысячная — промилле.
Процент обозначают знаком %, а промилле — знаком ‰:
1 % = 1
100
= 0,01; 56 % = 56
100
= 0,56;
1 ‰ = 1
1000
= 0,001; 56 ‰ = 56
1000
= 0,056.
Рациональные числа
Если на прямой p взять некоторую точку O в качестве на-
чала отсчета, выбрать одно из двух направлений и единичный
отрезок OE, то этим самым задается координатная прямая
(рис. 414).
Правообладатель Народная асвета
Народная
асвета

47. 347
Если от начала отсчета O на данной прямой в выбранном
направлении отложить отрезок, длина которого равна дан-
ному числу t, то получим точку A. Число t называют коор-
динатой точки A. Это записвают так: A(t). Для точек O и E
имеем соответственно: O(0) и E(1).
Луч OE координатной прямой называют положительным
лучом, другой ее луч — отрицательным лучом.
Точке B, симметричной точке A относительно начала от-
счета O, присваивается координата −t. Числа t и −t называют
противоположными числами.
Числа, которым соответствуют точки координатной пря-
мой, расположенные на положительном луче, называются по-
ложительными числами, они могут записываться как со зна-
ком +, так и без него: записи вида +1 и 1 обозначают одно и
то же число.
Числа, которым соответствуют точки координатной пря-
мой, расположенные на отрицательном луче, называются от-
рицательными числами. Отрицательные числа записывают-
ся со знаком –.
Число 0 не считают ни отрицательным, ни положительным.
Модулем ⏐t⏐ числа t называется само это число, если оно
положительно или равно нулю, и противоположное число,
если число t отрицательно:
⏐t⏐ =
t t
t t
,если положительное число или число 0
,если отрицател
—
—
,
− ььное число.
⎧
⎨
⎩
Чтобы сложить два числа с одинаковыми знаками, нужно
сложить их модули и перед суммой поставить их общий знак.
Чтобы сложить два числа с разными знаками, нужно из
большего модуля вычесть меньший и результат записать со
знаком того числа, модуль которого больше.
Чтобы из одного числа вычесть другое число, можно к умень-
шаемому прибавить число, противоположное вычитаемому.
Чтобы умножить два числа, нужно перемножить их моду-
ли и результат записать со знаком плюс, если множители име-
ют одинаковые знаки, и со знаком минус, если разные знаки.
Чтобы разделить одно число на другое, можно делимое
умножить на число, обратное делителю.
Натуральные числа называют еще положительными целы-
ми числами. Числа, противоположные натуральным числам,
Рис. 414
Правообладатель Народная асвета
Народная
асвета

48. 348
называют отрицательными целыми числами. Множество Z
целых чисел — это натуральные числа, числа, противополож-
ные натуральным, и число 0.
Целые числа вместе с дробными, как положительными,
так и отрицательными, вместе составляют множество Q ра-
циональных чисел.
Действительные числа
Во множестве рациональных чисел становятся всегда
выполнимыми вычитание и деление на число, отличное от
нуля. Но действие извлечения квадратного корня, обратное
действию возведения в квадрат, не всегда выполнимо. На-
пример, число 2 не является рациональным.
Рациональные числа представляются десятичными дро-
бями — конечными или бесконечными периодическими без
периода из одних девяток. Каждая десятичная дробь, как ко-
нечная, так и бесконечная периодическая, представляет не-
которое рациональное число. Бесконечные непериодические
десятичные дроби представляют иррациональные числа:
2 = 1,414 213 562 373 095 048 801 688 724 209 … .
К получению иррациональных чисел приводит не только
действие извлечения квадратного корня. Действия нахожде-
ния значений синуса, косинуса, тангенса, котангенса, за ред-
ким исключением, порождают иррациональные числа:
sin2° = 0,034 899 496 702 500 971 645 995 181 625 333 …;
tg89° = 57,289 961 630 759 424 687 278 147 537 113 … .
Иррациональным является и число π:
π = 3,141 592 653 589 793 238 462 643 383 279 … .
Рациональные числа вместе с иррациональными числами
составляют множество R действительных чисел.
Каждому рациональному чис-
лу соответствует единственная
точка координатной прямой, но
не каждая точка координатной
прямой имеет своей координа-
той рациональное число. На ри-
сунке 415 показано построение
точки, координата которой
есть длина l диагонали квад-Рис. 415
Правообладатель Народная асвета
Народная
асвета

49. 349
рата со стороной 2, а эта длина выражается числом 2 2, ко-
торое не является рациональным. Каждому действительному
числу соответствует единственная точка координатной пря-
мой, и каждая точка координатной прямой имеет координа-
той действительное число.
Сравнение действительных чисел
Для любых двух действительных чисел a и b истинно одно и
только одно из утверждений: a меньше b; a равно b; a больше b.
Отношения a меньше b; a равно b; a больше b передаются
формулами a b, a = b, a b соответственно и вводятся сле-
дующим определением:
a b ≡
опр
a − b 0; a = b ≡
опр
a − b = 0; a b ≡
опр
a − b 0.
Формулами a b, a ≠ b и a b обозначают отношения a
больше или равно b, a не равно b и a меньше или равно b.
Первое из этих отношений имеет место, если выполняется
хотя бы одно из отношений a b или a = b, второе — если не
выполняется отношение a = b, третье — если выполняется хо-
тя бы одно из отношений a b или a = b.
Формулой a x b обозначается отношение x больше a и
меньше b, которое имеет место, если выполняются отношения
a x и x b. Аналогично определяются отношения a x b,
a x b и a x b.
Отношение a = b называют равенством, отношения a b,
a b, a b, a ≠ b и a b — неравенствами. Неравенства a b
и a b называют строгими неравенствами, а неравенства
a b и a b — нестрогими неравенствами.
Отношение равно имеет такие свойства:
если a = b, то b = a (симметричность);
если a = b и b = c, то a = c (транзитивность).
Отношение меньше имеет такие свойства:
если a b, то b a;
если a b и b c, то a c (транзитивность);
если a b, то a + c b + c;
если a b и c 0, то ac bc;
если a b и c 0, то ac bc;
если a b и c d, то a + c b + d;
если a b, c d и a, c — положительные числа, то ac bd;
если a b и c d, то a − c b − d;
Правообладатель Народная асвета
Народная
асвета

50. 350
если a b и a и b — положительные числа, то 1
a
1
b
;
если a b и a и b — положительные числа и n — нату-
ральное число, то an
bn
.
Аналогичные свойства имеет и отношение больше.
Из двух натуральных чисел больше то, которое при счете
называется позже.
Натуральные числа и десятичные дроби сравнивают по-
разрядно, начиная со старшего разряда.
Из двух положительных обыкновенных дробей с равными
знаменателями больше та, у которой числитель больше. Из
двух положительных обыкновенных дробей с равными чис-
лителями больше та, у которой знаменатель меньше. Чтобы
сравнить две обыкновенные дроби с разными числителями
и знаменателями, можно эти дроби заменить равными им
дробями с равными знаменателями (или числителями), при-
ведя их к общему знаменателю (или числителю).
Из двух действительных чисел с разными знаками боль-
шим является положительное число. Число 0 больше любого
отрицательного числа и меньше любого положительного. Из
двух отрицательных действительных чисел больше то, мо-
дуль которого меньше. Из двух положительных действитель-
ных чисел больше то, модуль которого больше.
Средние величины
Средним арифметическим a чисел a1, a2, …, an называет-
ся их сумма, деленная на их количество n:
a =
a a a
n
n1 2+ + +K
.
Средним геометрическим g двух положительных чисел a1
и a2 называется квадратный корень из их произведения:
g = a a1 2 .
Среднее арифметическое a и среднее геометрическое g од-
них и тех же чисел связаны неравенством g a.
Свойства действий над числами
Сложение и умножение натуральных чисел имеют пере-
местительное и сочетательное свойства, а умножение по от-
ношению к сложению имеет распределительное свойство:
a + b = b + a;
a + (b + c) = (a + b) + c;
a b = b a;
a (b c) = (a b) c;
a (b + c) = a b + a c.
Правообладатель Народная асвета
Народная
асвета

51. 351
Число 0 имеет такие свойства:
a + 0 = 0 + a = a; a + (−a) = 0;
a − 0 = a; 0 − a = −a;
a 0 = 0 a = 0;
0 : a = 0, если a ≠ 0; выражение a : 0 не имеет значения.
Число 1 имеет такие свойства:
a 1 = 1 a = a; a 1
a
= 1;
1 : a = 1
a
, если a ≠ 0; a : 1 = a.
Пропорции
Отношением значений некоторой величины называ-
ют частное от деления одного из этих значений на другое.
Если делимое больше делителя, то отношение показывает, во
сколько раз первое значение больше другого, а если делимое
меньше делителя, то — какую часть первое значение состав-
ляет от другого.
Чтобы найти отношение значений величины, нужно при-
вести их к одной единице измерения и первое число разде-
лить на второе.
Равенство a
b
= c
d
двух отношений a
b
и c
d
называют про-
порцией.
Если есть пропорция a
b
= c
d
, то числа a и d называют край-
ними членами пропорции, а числа b и c — ее средними чле-
нами.
Если равенство a
b
= c
d
истинно, то соответствующая про-
порция называется правильной пропорцией, в противном слу-
чае — неправильной пропорцией.
Если пропорция правильная, то произведение ее крайних
членов равно произведению средних членов.
Если произведение крайних членов пропорции равно про-
изведению ее средних членов, то пропорция правильная.
Если поменять местами крайние члены правильной про-
порции или ее средние члены, то пропорция останется пра-
вильной:
если a
b
= c
d
, то d
b
= c
a
и a
c
= b
d
.
Правообладатель Народная асвета
Народная
асвета

52. 352
Степень с целым показателем
Для степени с целым показателем имеем такие определе-
ния:
a0
= 1, если a ≠ 0;
a1
= a;
an
= a a a
n
K
1 24 34
множителей
, если n — натуральное число и n 1;
a−p
= 1
ap
, если a ≠ 0, p — натуральное число.
Для любых положительных действительных значений a и
b и любых целых значений p и q верны равенства:
ap
aq
= ap + q
; (ab)p
= ap
bp
;
ap
: aq
= ap − q
;
a
b
p
= a
b
p
p
.
(ap
)q
= apq
;
Любое действительное число можно представить в стан-
дартном виде, т. е. записать произведением c 10n
, где
1 c 10, а n — целое число. Число n называют порядком
числа.
Арифметический квадратный корень имеет такие свой-
ства:
выражение a имеет значение, если a 0;
a2
= ⏐a⏐ верно при любом действительном значении пе-
ременной a;
если a 0 и b 0, то ab = a b и a b ≡ a b;
равенство a
b
= a
b
истинно, если a 0 и b 0.
Правообладатель Народная асвета
Народная
асвета

53. 353
Тригонометрические числовые выражения
Синусом угла α называется отношение, первый компонент
которого есть расстояние от произвольной точки M на одной
стороне угла величиной α до прямой, содержащей другую сто-
рону, а второй компонент — расстояние от точки M до вер-
шины A угла:
sinα = MX
MA
(рис. 416).
Косинусом угла α называется
отношение, первый компонент кото-
рого есть расстояние от вершины A
угла до проекции X произвольной
точки M одной стороны угла вели-
чиной α на прямую, содержащую другую сторону, а второй
компонент — расстояние от вершины A угла до точки M, при-
чем это отношение имеет знак плюс, если проекция X по-
падает на сторону угла, и знак минус, если на продолжение
стороны (рис. 417):
cos α
α
α
=
− <
⎧
⎨
⎪
⎩⎪
AX
AM
AX
AM
, если 90 ,
, если 90 180 .
°
° °
Тангенсом угла α называется от-
ношение синуса этого угла к его ко-
синусу:
tg α = sin
cos
.α
α
Котангенсом угла α называется отношение
косинуса этого угла к его синусу:
ctg α = cos
sin
.α
α
Синус, косинус, тангенс, котангенс острого
угла прямоугольного треугольника связаны с его
сторонами (рис. 418):
sinA = a
c
; cosA = b
c
; tg A = a
b
; ctg A = b
a
.
Рис. 417
Рис. 416
Рис. 418
Правообладатель Народная асвета
Народная
асвета

54. 354
Синус, косинус, тангенс, котангенс некоторых углов при-
ведены в следующей таблице.
Угол α, ° 0 30 45 60 90 120 135 150 180
Синус
угла α
0 1
2
2
2
3
2
1
3
2
2
2
1
2
0
Косинус
угла α
1
3
2
2
2
1
2
0 −
1
2
−
2
2
−
3
2
−1
Тангенс
угла α
0 3
3
1 3
Не
суще-
ствует
− 3 −1 −
3
3
0
Катангенс
угла α
Не
суще-
ствует
3 1 3
3
0 −
3
3
−1 − 3
Не
суще-
ствует
Синус, косинус, тангенс и котангенс одного и того же угла
связаны формулами:
sin2
α + cos2
α = 1; tgα ctgα = 1;
1 + tg2
α = 1
2
cos
;
α
1 + ctg2
α = 1
2
sin α
.
Для синуса, косинуса, тангенса и котангенса угла верны
формулы приведения:
sin(90° − α) = cosα; tg(90° + α) = –ctgα;
cos(90° − α) = sinα; ctg(90° + α) = –tgα;
tg(90° − α) = ctgα; sin(180° − α) = sinα;
ctg(90° − α) = tgα; cos(180° − α) = –cosα;
sin(90° + α) = cosα; tg(180° − α) = –tgα;
cos(90° + α) = –sinα; ctg(180° − α) = –ctgα.
АЛГЕБРА
Выражения
Выражение.
Тождественное преобразование выражения
В алгебре изучаются выражения с переменными, уравне-
ния, неравенства, функции. Основным из этих понятий яв-
ляется понятие выражения с переменными. Уравнение или
неравенство получается из двух выражений, если соединить
их знаком =, , , ≠, , . Функция возникает тогда, когда в
отношении выражения с переменными ставится вопрос о его
значениях при различных возможных значениях переменных.
Правообладатель Народная асвета
Народная
асвета

55. 355
Выражение с переменными образуется из чисел и перемен-
ных с помощью действий над числами, из которых вы знаете
сложение, вычитание, умножение, деление, возведение в целую
степень и извлечение квадратного корня, нахождение значений
синуса, косинуса, тангенса, котангенса. В зависимости от то-
го, какие действия использованы при образовании выражения,
его относят к тому или иному виду, отношения между кото-
рыми показывает схема, приведенная на рисунке 406 (с. 315).
Если в выражение с переменными подставить вместо каж-
дой переменной какое-либо ее значение, то получится число-
вое выражение, значение которого называют значением выра-
жения с переменными при выбранных значениях переменных.
Множество наборов значений переменных, при которых
выражение с переменными имеет значения, называют облас-
тью определения выражения.
Целое выражение имеет значения при любых значениях
входящих в него переменных.
Дробно-рациональное выражение имеет значения при тех
наборах значений входящих в выражение переменных, при
которых его знаменатель не равен нулю.
Иррациональное выражение при показателе корня, равном
двум, имеет значение при тех наборах значений переменных,
при которых его подкоренное выражение не меньше нуля.
Два выражения с одними и теми же переменными назы-
ваются тождественно равными, если при всех наборах зна-
чений переменных из области определения соответствующие
значения выражений равны.
Замена выражения тождественно равным ему выражением
называется тождественным преобразованием этого выражения.
Поскольку a − b = a + (−b), то выражение, образованное из дру-
гих выражений с помощью сложения и вычитания, можно за-
писать как сумму, которая называется алгебраической суммой.
Раскрытием скобок называется замена выражения
a(b1 + b2 + … + bn) выражением ab1 + ab2 + … + abn.
Вынесением общего множителя за скобки называется заме-
на выражения ab1 + ab2 + … + abn выражением a(b1 + b2 + … + bn).
Если слагаемые алгебраической суммы одинаковы или от-
личаются только числовыми множителями, то их называют
подобными слагаемыми. Замена суммы подобных слагаемых
тождественно равным ей одним слагаемым называется при-
ведением подобных слагаемых.
Правообладатель Народная асвета
Народная
асвета

56. 356
Целые выражения
Произведение чисел, переменных и их натуральных сте-
пеней называют одночленом.
Любой одночлен можно привести к стандартному виду,
т. е. представить произведением числового множителя, за-
писанного первым, и последующих степеней различных пе-
ременных. Этот числовой множитель называется коэффици-
ентом одночлена. Сумму показателей степеней всех перемен-
ных одночлена называют степенью одночлена.
Произведение двух одночленов и натуральную степень од-
ночлена можно заменить тождественно равным одночленом
стандартного вида.
Чтобы перемножить одночлены, нужно перемножить ко-
эффициенты, а показатели степеней одинаковых переменных
сложить.
Чтобы возвести в степень одночлен, нужно возвести в эту
степень каждый из множителей.
Алгебраическую сумму одночленов называют многочленом.
Одночлены, из которых состоит многочлен, называют чле-
нами многочлена. Одночлен также считают многочленом.
Многочлен из двух членов называют двучленом, а из трех
членов — трехчленом.
Члены многочлена, отличающиеся только знаками своих
коэффициентов, в сумме дают нуль. В этом случае говорят,
что они взаимно уничтожаются.
Многочлен, не имеющий подобных членов, все члены ко-
торого записаны в стандартном виде, называют многочленом
стандартного вида.
Любой многочлен можно привести к стандартному виду.
Сумму или разность любых многочленов можно предста-
вить многочленом стандартного вида.
При решении обратной задачи — представлении многочлена
суммой или разностью многочленов — пользуются правилами:
если при заключении в скобки членов многочлена перед
скобками поставлен знак плюс, то члены в скобках записы-
вают со своими знаками;
если при заключении в скобки членов многочлена перед
скобками поставлен знак минус, то члены в скобках записы-
вают с противоположными знаками.
Чтобы умножить одночлен на многочлен, нужно этот од-
ночлен умножить на каждый член многочлена и полученные
произведения сложить.
Правообладатель Народная асвета
Народная
асвета

57. 357
Чтобы многочлен разделить на одночлен, нужно каждый
член многочлена разделить на этот одночлен.
Чтобы вынести общий множитель членов многочлена за
скобки, нужно:
выделить этот общий множитель;
делением членов многочлена на общий множитель найти
многочлен, который записывается в скобках.
Чтобы умножить многочлен на многочлен, нужно каждый
член одного многочлена умножить на каждый член другого
многочлена и записать сумму полученных произведений.
При преобразованиях целых выражений могут использо-
ваться формулы сокращенного умножения:
(a + b)2
= a2
+ 2ab + b2
; (a − b)(a + b) = a2
− b2
;
(a − b)2
= a2
− 2ab + b2
; (a + b)(a2
− ab + b2
) = a3
+ b3
;
(a + b)3
= a3
+ 3a2
b + 3ab2
+ b3
; (a − b)(a2
+ ab + b2
) = a3
− b3
.
(a − b)3
= a3
− 3a2
b + 3ab2
− b3
;
Каждое целое выражение можно представить много-
членом стандартного вида. Целью преобразования целого
выражения в большинстве случаев как раз и является при-
ведение его к стандартному виду.
Иногда приходится решать обратную задачу — предста-
вить многочлен стандартного вида произведением нескольких
множителей-многочленов. Такое преобразование многочлена
называют разложением многочлена на множители.
При разложении многочлена на множители используют
способы: вынесение общего множителя за скобки; группиров-
ка; по формулам сокращенного умножения.
Квадратный трехчлен
Из целых выражений специально изучается квадратный
трехчлен, т. е. многочлен ax2
+ bx + c, где a, b, c — некоторые
числа, x — переменная, причем a ≠ 0.
Значения переменнай x, при которых квадратный трех-
член имеет своим значением число 0, называются корнями
квадратного трехчлена.
Числа a, b, c называют коэффициентами квадратного трех-
члена, число a — первым, или старшим, коэффициентом, чис-
ло b — вторым коэффициентом, число c — свободным членом.
Выражение b2
− 4ac называют дискриминантом квадрат-
ного трехчлена и обозначают D, т. е.
D = b2
− 4ac.
Правообладатель Народная асвета
Народная
асвета

58. 358
Если D 0, то квадратный трехчлен имеет два корня x1 и
x2, которые выражаются через его коэффициенты следующим
образом:
x1 =
− −b D
a2
и x2 =
− +b D
a2
.
Если D = 0, то квадратный трехчлен имеет один корень
x = − b
a2
.
Если D 0, то квадратный трехчлен не имеет корней.
Теорема о разложении квадратного трехчлена на линей-
ные множители: если дискриминант D квадратного трехчле-
на ах2
bх с положителен и х1 и х2 — его корни, то истинно
равенство ах2
bх с а(х х1)(х х2); если D 0 и х1 — его
корень, то ах2
bх с а(х х1)2
; если D 0, то квадратный
трехчлен на множители не раскладывается.
Теорема Виета: если x1 и x2 — корни квадратного трех-
члена ax2
+ bx + c, то
x1 + x2 = − b
a
и x1 x2 = c
a
.
Это утверждение остается в силе и при D 0, если х1 и х2
находить по общим формулам.
Теорема, обратная теореме Виета: если числа a, b, c, x1 и
x2 удовлетворяют условиям x1 + x2 = − b
a
и x1 x2 = c
a
, то x1 и
x2 — корни квадратного трехчлена ax2
+ bx + c.
Рациональные выражения
Множество рациональных выражений составляют целые
и дробно-рациональные выражения.
Любое рациональное выражение можно представить дро-
бью M
N
, где M и N — многочлены стандартного вида, которые
могут быть и числами. Такую дробь называют рациональной
дробью.
Целью преобразования рационального выражения являет-
ся, чаще всего, представление его рациональной дробью.
Правила действий над рациональными дробями такие же,
как и над обыкновенными дробями. Вместе с этими правила-
ми при преобразованиях рациональных выражений исполь-
зуются правила преобразований целых выражений, которые
являются частями рационального выражения, а также свой-
ства степени с целым показателем, в том числе и следующие:
если P ≠ 0 и Q ≠ 0, то P
Q
n−
= Q
P
n
.
Правообладатель Народная асвета
Народная
асвета

59. 359
Алгебраические выражения
Множество алгебраических выражений составляют рацио-
нальные и иррациональные выражения.
При преобразованиях иррациональных выражений ис-
пользуют правила действий над рациональными выражени-
ями, свойства степени с целым показателем и свойства ра-
дикалов.
Трансцендентные выражения
Из трансцендентных выражений вам известны тригоно-
метрические выражения. При преобразованиях этих выраже-
ний вы можете использовать определения синуса, косинуса,
тангенса, котангенса и известные вам формулы, связываю-
щие их друг с другом, а также формулы приведения.
Уравнения и неравенства
Из двух выражений с переменными образуется формула,
если выражения связать каким-либо отношением. В школь-
ной алгебре изучаются отношения равно, меньше, больше и
их отрицания — не равно, больше или равно, меньше или рав-
но. В соответствии с этим из двух выражений A и B образу-
ются формулы следующих видов:
A = B, A B, A B, A ≠ B, A B, A B.
Формула, которая превращается в истинное высказыва-
ние при любых наборах значений входящих в нее перемен-
ных, называется тождественно истинной формулой или
тождеством. Другие формулы называются формулами-за-
висимостями.
Формула-равенство A = B называется уравнением, форму-
лы-неравенства A B, A B, A ≠ B, A B, A B — неравен-
ствами с переменными.
Областью определения формулы называется множество
тех наборов значений переменных, входящих в выражения
A и B, при которых имеют значения оба выражения A и B.
Число, превращающее уравнение в истинное высказыва-
ние, называют корнем уравнения.
Решить уравнение означает найти все его корни или ус-
тановить, что их нет.
Правообладатель Народная асвета
Народная
асвета

60. 360
Число, превращающее неравенство с переменной в истин-
ное высказывание, называют решением неравенства.
Решить неравенство означает найти все его решения или
установить, что их нет.
Из формул образуют их системы и совокупности.
Системой формул называется формула, состоящая из
двух или большего числа формул и являющаяся истинной
при тех и только тех наборах значений переменных, при ко-
торых истинна каждая из формул.
Система, состоящая из формул A и B, обозначается
A
B
,
.
⎧
⎨
⎩
Совокупностью формул называется формула, состоящая
из двух или большего числа формул и являющаяся истин-
ной при тех и только тех наборах значений переменных, при
которых истинна хотя бы одна из формул. Совокупность, со-
стоящая из формул A и B, обозначается
A
B
,
.
⎡
⎣
⎢
Каждая пара значений переменных, удовлетворяющая си-
стеме или совокупности формул с двумя переменными, назы-
вается решением системы или совокупности. Аналогично оп-
ределяется понятие решения системы или совокупности фор-
мул с другим количеством переменных.
Решить систему или совокупность означает найти все ее
решения или установить, что их нет.
Решение уравнений, неравенств, их систем и совокупно-
стей часто предусматривает сведение их к стандартным урав-
нениям или неравенствам. При этом полученное в результате
преобразований уравнение, неравенство, система или совокуп-
ность должны иметь те же решения, что и исходное уравне-
ние, неравенство, система или совокупность. В таком случае
говорят о равносильных уравнениях, неравенствах, системах,
совокупностях. Замена уравнения, неравенства, системы, со-
вокупности равносильным уравнением, неравенством, систе-
мой, совокупностью называется преобразованием равносиль-
ности.
Преобразованиями равносильности уравнений или нера-
венств являются:
• перенос слагаемого из одной части уравнения или нера-
венства в другую с изменением его знака;
Правообладатель Народная асвета
Народная
асвета

61. 361
• умножение или деление обеих частей уравнения на одно
и то же не равное нулю число;
• умножение или деление обеих частей неравенства на од-
но и то же положительное число;
• умножение или деление обеих частей неравенства на од-
но и то же отрицательное число с заменой знака неравенства
знаком противоположного смысла;
• возведение обеих частей уравнения или неравенства в од-
ну и ту же нечетную степень.
При решении уравнений пользуются и преобразованиями
следования, т. е. преобразованиями, при которых все кор-
ни данного уравнения являются корнями полученного урав-
нения. Примером преобразования следования является воз-
ведение обеих частей уравнения в одну и ту же четную сте-
пень. Преобразование следования может приводить к появле-
нию побочных корней, т. е. таких чисел, которые являются
корнями полученного уравнения, но не являются корнями
исходного. Поэтому при использовании преобразований сле-
дования обязательным этапом решения уравнения является
проверка того, являются ли полученные числа корнями дан-
ного уравнения.
При решении уравнений и неравенств используются та-
кие типичные приемы, как введение вспомогательной пе-
ременной, разложение на множители, перебор случаев, све-
дение к системе, использование графических представлений,
использование свойств функций.
С разложением на множители связан метод интервалов,
с помощью которого можно решать рациональные неравен-
ства.
Неравенство 2
1
2
3 2
3
2 1t t t+ + −
+ сводится к неравенству
( )( )
( )( )( )
,
t t
t t t
+ −
+ + −
1 4
3 3 2 2 1
0 для которого метод интервалов (рис. 419)
дает ответом множество − −( ] − +[ )3 1 42
3
1
2
; ; ; .
Рис. 419
Правообладатель Народная асвета
Народная
асвета

62. 362
Чтобы ответить на вопрос
о количестве решений системы
y
x y
x
=
− + + =
⎧
⎨
⎪
⎩⎪
1
1 1 42 2
,
( ) ( ) ,
удобно использовать графичес-
кий способ решения. Постро-
ив графики зависимостей y = 1
x
и (x − 1)2
(y 1)2
= 4 (рис. 420),
замечаем, что они имеют 4 точ-
ки пересечения. Поэтому система имеет 4 решения.
Сведения о решении линейных, квадратных и двучленных
уравнений приведены в следующей таблице.
Уравнение Корни
ax = b
b
a
, если a ≠ 0
ax2
+ bx + c = 0 −b b ac
a
± −2
4
2
, если D = b2
− 4ac 0
xn
= a
a
n
, если n — нечетное число;
± a
n
, если n — четное число и a 0
Сведения о решении линейных и квадратных неравенств
даются в схемах, приведенных на рисунках 421 и 422.
При решении систем уравнений стремятся уменьшить ко-
личество переменных и получить уравнение с одной перемен-
ной, которое позволит найти ее значения, а затем для каж-
дого из полученных значений ищутся значения остальных пе-
ременных. Исключить одну из переменных из системы двух
линейных уравнений с двумя переменными можно способом
подстановки или способом алгебраического сложения.
Уравнение, неравенство или система могут содержать две или
больше переменных, причем одна из них считается переменной
уравнения, а остальные рассматриваются как параметры, т. е. их
значения считаются фиксированными. В таком случае говорят
об уравнении, неравенстве или системе с параметрами.
Решить уравнение, неравенство или систему с парамет-
рами означает для каждого набора значений параметров най-
ти корни или решения соответствующего уравнения, неравен-
ства или системы.
Рис. 420
Правообладатель Народная асвета
Народная
асвета

63. 363
Рис. 421
Рис. 422
Правообладатель Народная асвета
Народная
асвета

64. 364
Координаты и функции
Если на прямой выбраны две точки O и E и с ними сопо-
ставлены числа 0 и 1 соответственно (см. рис. 414), то говорят,
что на прямой задана система координат, а саму прямую на-
зывают координатной прямой или координатной осью. Точ-
ку O называют началом координат, а отрезок OE — единичным
отрезком. Соответствие между точками координатной пря-
мой и действительными числами взаимно однозначное: каж-
дой точке координатной прямой соответствует единственное
действительное число, а каждому действительному числу со-
ответствует единственная точка координатной прямой. Чис-
ло x, соответствующее точке A координатной прямой, назы-
вают координатой этой точки и записывают A(x).
Если на каждой из двух перпендикулярных прямых за-
даны системы координат с общим началом в точке O пере-
сечения прямых, то говорят, что задана система координат
на плоскости. Плоскость, на которой задана система коорди-
нат, называется координатной плоскостью, одну из коорди-
натных прямых, обычно горизонтальную, называют осью аб-
сцисс, другую — осью ординат. Соответствие между точками
координатной плоскости и парами действительных чисел вза-
имно однозначное: каждой точке координатной плоскости со-
ответствует единственная пара действительных чисел, а каж-
дой паре действительных чисел соответствует единственная
точка координатной плоскости. Числа x и y пары (x; y), соот-
ветствующей точке M координатной плоскости, называют ко-
ординатами этой точки, причем первая координата называет-
ся абсциссой, вторая — ординатой. Это записывают M(x; y).
Если есть точки A(x1) и B(x2), то расстояние между ними
выражается числом ⏐x1 − x2⏐, а если даны точки A(x1; y1) и
B(x2; y2), то числом ( ) ( )x x y y1 2
2
1 2
2
− + − (рис. 423).
Зависимость одной переменной y от другой x, при которой
каждому значению переменной x из некоторого множества D
соответствует единственное значение переменной y, называет-
ся функциональной зависимостью или функцией.
Функциональную зависимость переменной y от перемен-
ной x обозначают y = f(x) или y = y(x). При этом переменную x
называют аргументом функции.
Множество тех значений, которые может принимать аргу-
мент функции, называется областью определения функции, а
Правообладатель Народная асвета
Народная
асвета

65. 365
множество тех значений, кото-
рые может принимать зависи-
мая переменная y, — областью
значений функции (см. рис. 45).
Область определения функции
y = f(x) обозначают символом
D(y), а область значений — E(y).
Графиком функции y = f(x)
называется множество всех то-
чек координатной плоскости,
абсциссы которых равны значе-
ниям аргумента, а ординаты —
соответствующим значениям
функции.
Если аргумент функции принимает только натуральные
значения, то такую функцию называют последовательностью.
Арифметической прогрессией называется последователь-
ность, в которой каждый следующий член получается при-
бавлением к предыдущему одного и того же числа d, которое
называется разностью прогрессии. Последовательность (an)
является арифметической прогрессией тогда и только тог-
да, когда любой ее член, начиная со второго, равен среднему
арифметическому двух соседних членов:
an =
a an n− ++1 1
2
.
Формулы
an = a1 + (n − 1)d и Sn =
a an1
2
+
n
дают возможность найти n-ный член арифметической про-
грессии и сумму n ее первых членов.
Геометрической прогрессией называется последователь-
ность, в которой каждый следующий член получается из пре-
дыдущего умножением на одно и то же не равное нулю число q,
которое называется знаменателем прогрессии. Последова-
тельность (bn) является геометрической прогрессией тогда и
только тогда, когда квадрат каждого ее члена, начиная со вто-
рого, равен произведению двух соседних с ним членов:
bn
2
= bn − 1bn + 1.
Для нахождения n-ого члена геометрической прогрессии и
суммы первых n ее членов можно использовать формулы:
bn = b1 qn − 1
и Sn = b1
q
q
n
−
−
1
1
.
Рис. 423
Правообладатель Народная асвета
Народная
асвета

66. 366
ГЕОМЕТРИЯ
Две прямые
Две прямые a и b могут быть параллельными (рис. 424)
или пересекающимися (рис. 425).
Рис. 424 Рис. 425
Пересекающиеся прямые разделяют плоскость на четыре
угла, пары которых имеют специальные названия.
Углы 1 и 2, которые имеют общую сторону, называют
смежными, а углы 1 и 3, стороны каждого из которых явля-
ются продолжениями сторон другого угла, — вертикальны-
ми. Смежные углы вместе составляют 180°, а вертикальные
углы равны друг другу.
Три прямые
Среди трех прямых a, b, c может не быть параллельных
прямых (рис. 426) или такие прямые могут быть. Если есть
параллельные прямые a и b, то третья прямая c может быть
параллельной им (рис. 427) или пересекать их (рис. 428).
Если две прямые a и b пересечены третьей прямой, то обра-
зуются 8 углов (рис. 429). Углы 1 и 5, 2 и 6, 3 и 7, 4 и 8 на-
зываются соответственными, углы 3 и 6, 4 и 5 — внут-
ренними односторонними, углы 3 и 5, 4 и 6 — внутренними
накрест лежащими.
Свойства параллельных прямых: если прямые a и b па-
раллельны, то соответственные углы равны, внутренние на-
крест лежащие углы равны, а внутренние односторонние вме-
сте составляют 180°.
Признаки параллельных прямых: две прямые параллель-
ны, если соответственные углы, образовавшиеся при пересе-
чении их третьей прямой, равны, или внутренние накрест
лежащие углы равны, или внутренние односторонние углы
вместе составляют 180°.
Три попарно пересекающиеся прямые выделяют из плос-
кости треугольник (рис. 430).
Правообладатель Народная асвета
Народная
асвета

67. 367
Треугольник
Свойства треугольника (рис. 431):
сумма внутренних углов равна 180°;
∠A + ∠B + ∠C = 180°;
каждая сторона треугольника мень-
ше суммы двух других его сторон и
больше их разности; b − c a b + c;
a − c b a + c; a − b c a + b;
против большего угла лежит боль-
шая сторона; если ∠A ∠C, то a c;
против большей стороны лежит боль-
ший угол; если a c, то ∠A ∠C;
теорема косинусов: квадрат стороны равен сумме квад-
ратов двух других сторон без удвоенного произведения этих
сторон на косинус угла между ними; a2
= b2
+ c2
− 2bccosA;
теорема синусов: стороны пропорциональны синусам про-
тиволежащих углов;
a
Asin
= b
Bsin
= c
Csin
.
Кроме сторон и углов, треугольник имеет и другие эле-
менты.
Рис. 431
Рис. 430Рис. 429
Рис. 427 Рис. 428Рис. 426
Правообладатель Народная асвета
Народная
асвета

68. 368
Внешний угол треугольника — угол, смежный с его внут-
ренним углом (рис. 432).
Внешний угол треугольника равен сумме двух его внут-
ренних углов, не смежных с ним; ∠BAD = ∠B + ∠C.
Средняя линия треугольника — отрезок, соединяющий се-
редины двух его сторон (рис. 433).
Средняя линия треугольника параллельна третьей стороне
и равна ее половине; MN AB, MN = 1
2
AB.
Медиана треугольника — отрезок, соединяющий вер-
шину треугольника с серединой противолежащей стороны
(рис. 434).
Медианы треугольника пересекаются в одной точке и делят-
ся ею в отношении 2 : 1, если считать от вершины (рис. 435);
АG : GА1 = BG : GB1 = CG : GC1 = 2 : 1.
Биссектриса треугольника — отрезок биссектрисы угла
треугольника, заключенный между его вершиной и противо-
лежащей стороной (рис. 436).
Биссектриса треугольника делит противолежащую сто-
рону на части, пропорциональные прилежащим сторонам;
BA
CA
1
1
= AB
AC
. Биссектрисы треугольника пересекаются в одной
точке (рис. 437).
Рис. 435 Рис. 436
Рис. 432 Рис. 433 Рис. 434
Правообладатель Народная асвета
Народная
асвета

69. 369
Высота треугольника — перпендикуляр, опущенный из
вершины треугольника на прямую, проходящую через про-
тивоположную его сторону (рис. 438).
Прямые, содержащие высоты треугольника, пересекаются
в одной точке (рис. 439).
Площадь треугольника равна половине произведения сто-
роны и проведенной к ней высоты, или произведению высо-
ты треугольника и перпендикулярной ей средней линии, или
половине произведения двух его сторон и синуса угла меж-
ду ними, или квадратному корню из произведения полупе-
риметра и трех разностей полупериметра с каждой стороной,
или произведению полупериметра и радиуса вписанной
окружности, или произведению трех сторон треугольника,
разделенному на учетверенный радиус описанной окруж-
ности (рис. 440);
p = 1
2
(AB + BC + CA);
S = 1
2
BC AA1 = AA1 MN =
= 1
2
AB AC sin BAC =
= p p AB p BC p CA( )( )( )− − − = pr =
=
AB BC CA
R4
.
Рис. 440
Рис. 437 Рис. 438 Рис. 439
Правообладатель Народная асвета
Народная
асвета

70. 370
Прямоугольный треугольник
Два угла треугольника обязательно
острые, а третий — больший — его угол
может быть и острым (рис. 441), и пря-
мым (рис. 442), и тупым (рис. 443). В со-
ответствии с этим треугольники разделяют
на остроугольные, прямоугольные, тупо-
угольные.
Свойства прямоугольного треугольни-
ка (рис. 444):
острые углы вместе составляют 90°;
∠A + ∠B = 90°;
теорема Пифагора: квадрат гипоте-
нузы равен сумме квадратов катетов;
AB2
= AC2
+ BC2
;
если катет лежит против угла в 30°, то
он равен половине гипотенузы;
если катет равен половине гипотенузы,
то он лежит против угла в 30°;
медиана, проведенная к гипотенузе,
равна половине этой гипотенузы и яв-
ляется радиусом описанной окружности;
CC2 = AC2 = BC2;
высота прямоугольного треугольника,
проведенная к гипотенузе, является сред-
ним геометрическим отрезков, на которые
она разделяет гипотенузу, а катет явля-
ется средним геометрическим гипотенузы
и проекции этого катета на гипотенузу;
CC1 = AC BC1 1 , AC = AB AC1 ,
BC = AB BC1 ;
синус острого угла равен отношению
противолежащего катета к гипотенузе; ко-
синус острого угла равен отношению прилежащего катета к
гипотенузе; тангенс острого угла равен отношению проти-
волежащего катета к прилежащему; котангенс острого угла
равен отношению прилежащего катета к противолежащему;
sinA = BC
AB
; cosA = AC
AB
; tg A = BC
AC
; ctg A = AC
BC
.
Рис. 444
Рис. 443
Рис. 442
Рис. 441
Правообладатель Народная асвета
Народная
асвета

71. 371
Признаки прямоугольного треугольника. Треугольник яв-
ляется прямоугольным, если:
сумма двух каких-нибудь его углов равна 90°;
квадрат большей его стороны равен сумме квадратов двух
других сторон;
одна из его медиан равна половине стороны, к которой
проведена.
Равнобедренный треугольник
Если треугольник имеет равные стороны, его называют рав-
нобедренным (рис. 445). Равнобедренный треугольник с тре-
мя равными сторонами называют равносторонним (рис. 446).
Свойства равнобедренного треугольника (рис. 447):
углы при основании равны; ∠A = ∠C;
медиана, биссектриса, высота, проведенные к основанию,
совпадают; если BB1 — медиана, то BB1 — биссектриса и вы-
сота; если BB1 — биссектриса, то BB1 — медиана и высота;
если BB1 — высота, то BB1 — биссектриса и медиана.
Рис. 445 Рис. 446 Рис. 447
Признаки равнобедренного треугольника. Треугольник
является равнобедренным, если:
два его угла равны;
медиана и высота, или медиана и биссектриса, или высота
и биссектриса, проведенные из одной вершины, совпадают.
Равенство фигур
Равные фигуры — фигуры, совпадающие при наложении.
Признаки равенства треугольников. Треугольники яв-
ляются равными, если они имеют равные:
Правообладатель Народная асвета
Народная
асвета

72. 372
угол и прилежащие к нему стороны;
сторону и прилежащие к ней углы;
три стороны.
Признаки равенства прямоугольных треугольников. Пря-
моугольные треугольники являются равными, если у них со-
ответственно равны:
катеты;
катет и прилежащий к нему острый угол;
гипотенуза и острый угол;
гипотенуза и катет.
Подобие фигур
Теорема Фалеса. Если на одной стороне угла отложить
равные отрезки и через их концы провести параллельные
прямые, пересекающие другую сторону угла, то эти прямые
на другой стороне высекают также равные отрезки.
Подобные треугольники — треугольники, углы которых
попарно равны, а соответственные стороны пропорциональны.
Подобные многоугольники с одинаковым количеством сто-
рон — многоугольники, углы которых попарно равны, а соот-
ветствующие стороны пропорциональны. При этом отношение
соответствующих сторон называют коэффициентом подобия.
Фигура Φ называется подобной фигуре Φ1 с коэффициен-
том подобия k, если между точками фигур Φ и Φ1 можно уста-
новить соответствие, при котором каждой точке A фигуры Φ
соответствует единственная точка A1 фигуры Φ1, и наоборот,
и при этом если точкам X и Y фигуры Φ соответствуют
точки X1 и Y1 фигуры Φ1, то всегда XY
X Y1 1
= k.
Признаки подобия треугольников. Треугольники являют-
ся подобными, если у них:
имеется по равному углу, а прилежащие к нему стороны
пропорциональны;
имеется по два равных угла;
все три стороны пропорциональны.
Отношение любых соответственных линейных элементов
подобных треугольников равно коэффициенту подобия. От-
ношение периметров подобных многоугольников равно ко-
эффициенту подобия. Отношение площадей подобных мно-
гоугольников равно квадрату коэффициента подобия.
Правообладатель Народная асвета
Народная
асвета

73. 373
Окружность и круг
Отношение длины C окружности к ее диа-
метру d является одним и тем же для лю-
бой окружности (рис. 448). Это отношение
выражается числом, которое обозначается π:
π = C
d
= 3,141592… .
Длина C окружности, площадь S соответ-
ствующего круга и их радиус r связаны фор-
мулами: C = 2πr; S = πr2
; S = C
2
r.
Окружность и угол
Угол, вершина которого находится
в центре круга, называется централь-
ным углом.
Угол, вершина которого принадле-
жит окружности, а стороны имеют с
окружностью общие точки, называется
вписанным углом (рис. 449).
Вписанный угол измеряется поло-
виной дуги, на которую он опирается.
Вписанный угол, который опирает-
ся на диаметр, является прямым.
Вписанные углы, опирающиеся на одну дугу, равны.
Угол с вершиной внутри круга измеряется полусуммой
дуг, одна из которых заключена между сторонами данного
угла, а другая — между сторонами угла, вертикального дан-
ному.
Угол, вершина которого находится вне круга, а стороны
пересекают окружность, измеряется полуразностью дуг, ко-
торые данный угол высекает из окружности.
Окружность и прямая
Секущая — прямая, имеющая с окружностью две общие
точки (рис. 450).
Касательная — прямая, имеющая с окружностью одну
общую точку (см. рис. 450).
Свойство касательной. Касательная перпендикулярна
радиусу, проведенному в точку касания.
Рис. 448
Рис. 449
Правообладатель Народная асвета
Народная
асвета

74. 374
Признак касательной. Прямая явля-
ется касательной, если она проходит че-
рез точку окружности и перпендикуляр-
на радиусу, проведенному в эту точку.
Угол между касательной и секущей,
проведенной через точку касания, из-
меряется половиной дуги, которую этот
угол заключает.
Произведение частей хорды, на ко-
торые она разделяется своей внутренней
точкой, есть величина постоянная, рав-
ная r2
− a2
, где r — радиус круга, a — расстояние от центра
до выбранной точки.
Если секущая проходит через точку вне круга, то про-
изведение отрезков, соединяющих эту точку с точками пере-
сечения секущей с окружностью, есть величина постоянная,
равная a2
− r2
, где r — радиус круга, a — расстояние от цент-
ра до выбранной точки.
Если секущая и касательная проходят через данную точку
вне круга, то произведение отрезков секущей, соединяющих
эту точку с точками пересечения секущей с окружностью,
равно квадрату отрезка касательной с концами в данной точ-
ке и точке касания.
Отрезки двух касательных, проведенных через одну точ-
ку, заключенные между этой точкой и точками касания, рав-
ны друг другу.
Окружность и треугольник
Окружность, вписанная в многоуголь-
ник — окружность, касающаяся всех сто-
рон многоугольника.
Окружность, описанная около много-
угольника — окружность, проходящая че-
рез все вершины многоугольника.
Центр вписанной в треугольник окруж-
ности совпадает с точкой пересечения его
биссектрис.
Центр описанной около треугольника окружности совпа-
дает с точкой пересечения серединных перпендикуляров к его
сторонам (рис. 451).
Рис. 451
Рис. 450
Правообладатель Народная асвета
Народная
асвета

75. 375
Радиусы r и R вписанной и описанной окружностей свя-
заны с другими элементами треугольника формулами:
r = S
p
; R = abc
S4
; a
Asin
= 2R.
Четырехугольник
Плоская замкнутая четырехзвенная ломаная выделяет
из плоскости четырехугольник. Четырехугольник на рисун-
ке 452 выпуклый, а на рисунке 453 невыпуклый. Обычно рас-
сматривают выпуклые четырехугольники.
Рис. 452 Рис. 453 Рис. 454
Свойства четырехугольника:
сумма внутренних углов равна 360°;
середины сторон четырехугольника являются вершинами
параллелограмма (рис. 454);
площадь четырехугольника равна половине произведения
его диагоналей и синуса угла между ними.
Трапеция
Трапеция — четырехугольник, у которого две стороны па-
раллельны, а две другие — нет (рис. 455).
Свойства трапеции (рис. 456):
сумма углов, прилежащих к боковой стороне, равна 180°;
∠A + ∠B = 180°; ∠C + ∠D = 180°;
Рис. 456Рис. 455
Правообладатель Народная асвета
Народная
асвета

76. 376
средняя линия трапеции параллельна ее основаниям и
равна их полусумме; MN AD, MN BC, MN = 1
2
(AD + BC);
площадь трапеции равна произведению ее средней линии
и высоты; SABCD = MN BB1;
из треугольников, на которые диагонали разделяют тра-
пецию, треугольники, прилежащие к ее основаниям, подоб-
ные, а треугольники, прилежащие к боковым сторонам, рав-
новеликие; AOD BOC; SAOB = SDOC.
Признаки четырехугольника с параллельными сторонами.
Четырехугольник имеет параллельные стороны, если:
сумма углов, прилежащих к какой-нибудь стороне, рав-
на 180°;
отрезок, соединяющий середины противоположных сторон
четырехугольника, равен полусумме двух других его сторон;
из четырех треугольников, на которые диагонали разделя-
ют четырехугольник, два треугольника, прилежащие к про-
тивоположным сторонам, равновелики.
Параллелограмм
Параллелограмм — четырехугольник, имеющий две пары
параллельных сторон (рис. 457).
Рис. 458Рис. 457
Свойства параллелограмма (рис. 458):
сумма углов, прилежащих к любой его стороне, равна
180°; ∠A + ∠B = 180°, и ∠B + ∠C = 180°, и ∠C + ∠D = 180°, и
∠D + ∠A = 180°;
его противоположные стороны параллельны и равны;
AD BC и AB CD; AD = BC и AB = CD;
Правообладатель Народная асвета
Народная
асвета

77. 377
его противоположные углы равны; ∠A = ∠C и ∠B = ∠D;
точка пересечения диагоналей делит их пополам; AO = CO;
BO = DO;
точка пересечения диагоналей является центром симмет-
рии параллелограмма;
площадь равна произведению стороны и проведенной к
ней высоты; SABCD = AD BB1.
Признаки параллелограмма. Четырехугольник ABCD яв-
ляется параллелограммом, если:
суммы углов, прилежащих к каким-нибудь двум
смежным сторонам, равны 180° каждая; ∠A + ∠B = 180°
и ∠B + ∠C = 180°, или ∠B + ∠C = 180° и ∠C + ∠D = 180°,
или ∠C + ∠D = 180° и ∠D + ∠A = 180°, или ∠D + ∠A = 180°
и ∠A + ∠B = 180°;
его противоположные стороны равны; AD = BC и AB = CD;
он имеет пару противоположных параллельных и равных
сторон; AD BC и AD = BC или AB = CD и AB CD;
его противоположные углы равны; ∠A = ∠C и ∠B = ∠D;
его диагонали точкой пересечения делятся пополам;
AO = CO; BO = DO.
Прямоугольник
Прямоугольник — параллелограмм, у которого имеется
прямой угол (рис. 459).
Рис. 459 Рис. 460
Свойства прямоугольника (рис. 460):
все его углы равны друг другу и прямые; ∠A = ∠B =
= ∠C = ∠D = 90°;
его диагонали равны; AC = BD;
серединные перпендикуляры к его сторонам являются
осями симметрии;
его площадь равна произведению смежных сторон;
SABCD = AB AD.
Правообладатель Народная асвета
Народная
асвета

78. 378
Признаки прямоугольника. Параллелограмм ABCD явля-
ется прямоугольником, если:
его диагонали равны; AC = BD;
серединный перпендикуляр к какой-нибудь стороне па-
раллелограмма является его осью симметрии; MN — ось сим-
метрии или PQ — ось симметрии.
Ромб
Ромб — параллелограмм, у которого имеются равные
смежные стороны (рис. 461).
Рис. 461 Рис. 462
Свойства ромба (рис. 462):
все его стороны равны друг другу; AB = BC = CD = DA;
его диагонали перпендикулярны; AC BD;
его диагонали делят углы пополам; ∠ABD = ∠CBD и
∠BАС = ∠DАС;
прямые, которые содержат его диагонали, являются ося-
ми симметрии;
его площадь равна половине произведения диагоналей;
SABCD = 1
2
AC BD.
Признаки ромба. Параллелограмм ABCD является ромбом,
если:
его диагонали перпендикулярны; AC BD;
его диагонали делят углы пополам; ∠ABD = ∠CBD
и ∠BCA = ∠DCA;
прямые, которые содержат его диагонали, являются ося-
ми симметрии.
Правообладатель Народная асвета
Народная
асвета

79. 379
Квадрат
Квадрат — прямоугольник, у ко-
торого есть равные смежные сторо-
ны, или ромб, у которого есть пря-
мой угол (рис. 463).
Поскольку квадрат является и
прямоугольником, и ромбом, то у не-
го имеются все свойства прямоуголь-
ника и все свойства ромба.
Окружность и четырехугольник
Свойство описанного четырехугольника (рис. 464): сум-
мы противоположных сторон равны.
Признак описанного четырехугольника. Четырехуголь-
ник является описанным около окружности, если у него рав-
ны суммы противоположных сторон.
Свойство вписанного четырехугольника (рис. 465):
суммы противоположных углов равны 180°; ∠A + ∠C =
= ∠B + ∠D = 180°;
произведение диагоналей равно сумме произведений
противоположных сторон; AC BD = AB CD + AD BC.
Рис. 464 Рис. 465
Признаки вписанного четырехугольника. Четырехуголь-
ник ABCD является вписанным в окружность, если:
сумма противоположных углов равна 180°; ∠A + ∠C =
= ∠B + ∠D = 180°;
углы, каждый из которых образован стороной и диа-
гональю и которые опираются на одну сторону, равны;
∠ACB = ∠ADB, или ∠BAC = ∠BDC, или ∠CAD = ∠CBD, или
∠ACD = ∠ABD.
Рис. 463
Правообладатель Народная асвета
Народная
асвета

80. 380
Таблицызначенийтригонометрическихфункций
sin0123456789
00,00000,01750,03490,05230,06980,08720,10450,12190,13920,1564
10,17360,19080,20790,22500,24190,25880,27560,29240,30900,3256
20,34200,35840,37460,39070,40670,42260,43840,45400,46950,4848
30,50000,51500,52990,54460,55920,57360,58780,60180,61570,6293
40,64280,65610,66910,68200,69470,70710,71930,73140,74310,7547
50,76600,77710,78800,79860,80900,81920,82900,83870,84800,8572
60,86600,87460,88290,89100,89880,90630,91350,92050,92720,9336
70,93970,94550,95110,95630,96130,96590,97030,97440,97810,9816
80,98480,98770,99030,99250,99450,99620,99760,99860,99940,9998
cos0123456789
01,0000,99980,99940,99860,99760,99620,99450,99250,99030,9877
10,98480,98160,97810,97440,97030,96590,96130,95630,95110,9455
20,93970,93360,92720,92050,91350,90630,89880,89100,88290,8746
30,86600,85720,84800,83870,82900,81920,80900,79860,78800,7771
40,76600,75470,74310,73140,71930,70710,69470,68200,66910,6561
50,64280,62930,61570,60180,58780,57360,55920,54460,52990,5150
60,50000,48480,46950,45400,43840,42260,40670,39070,37460,3584
70,34200,32560,30900,29240,27560,25880,24190,22500,20790,1908
80,17360,15640,13920,12190,10450,08720,06980,05230,03490,0175
Правообладатель Народная асвета
Народная
асвета

81. 381
tg0123456789
00,00000,01750,03490,05240,06990,08750,10510,12280,14050,1584
10,17630,19440,21260,23090,24930,26790,28670,30570,32490,3443
20,36400,38390,40400,42450,44520,46630,48770,50950,53170,5543
30,57740,60090,62490,64940,67450,70020,72650,75360,78130,8098
40,83910,86930,90040,93250,96571,00001,03551,07241,11061,1504
51,19181,23491,27991,32701,37641,42821,48261,53991,60031,6643
61,73201,8041,8811,9632,0502,1452,2462,3562,4752,605
72,7472,9043,0783,2713,4873,7324,0114,3314,7055,145
85,6716,3147,1158,1449,51411,4314,3019,0828,6457,29
ctg0123456789
0—57,2928,6419,0814,3011,439,5148,1447,1156,314
15,6715,1454,7054,3314,0113,7323,4873,2713,0782,904
22,7472,6052,4752,3562,2462,1452,0501,9631,8811,8040
31,73201,66431,60031,53991,48261,42821,37641,32701,27991,2349
41,19181,15041,11061,07241,03551,00000,96570,93250,90040,8693
50,83910,80980,78130,75360,72650,70020,67450,64940,62490,6009
60,57740,55430,53170,50950,48770,46630,44520,42450,40400,3839
70,36400,34430,32490,30570,28670,26790,24930,23090,21260,1944
80,17630,15840,14050,12280,10510,08750,06990,05240,03490,0175
Правообладатель Народная асвета
Народная
асвета

82. 382
ОТВЕТЫ
Раздел 1
16. 0 r 2 13. 23. а) 1; 9; б) 3; 7; в) 4; 6; г) 1; 11; д) 2; 12; е) 5 2 17± ;
ж) 5 2 13± ; з) 5 3 2± . 26. а) 20; 36; б) 28; 25; в) 2; 45; г) 2; 35.
27. а) 114 см2
; б) 210 см2
. 28. а) 40 м; б) 63 дм. 29. а) 660 м2
; б) 1092 м2
.
30. а) 99 м и 39 21
101
м; б) 80 мм и 35 5
41
мм. 31. 8 м. 33. 3 м, 5 м, 7 м.
34. 660 см, 154 см, 220 см, 286 см. 35. а) 20
3
см, 20
3
см, 10
3
см, 10
3
см,
10
3
19 см; б) 20
3
см, 10 7
3
см, 10
3
см. 74. а) x(x 1)(x3
x2
1);
б)x2
(x 3)(x 2)(x 2);в)(x 2y)(x y);г)(x y)(x2
xy 2y2
).75.а)[ 17,8; );
б) ( 2,6; ); в) −9 3
8
3 3
8
; ; г) 5. 77. в) 30°; 75°; 75°. 78. 10°; 20°; 150°. 79. а) 80°;
140°; 140° или 140°; 110°; 110°; б) 80°; 140°; 140°. 80. 28,5 см, 30 см, 31,5 см.
108. а) 1; б) 3; в) 2; г) 4 ± 7. 109. а) − 2
3
; б) − 1
3
; 2; в) 3; 1; г) 2; −
+1 17
2
.
110. 3
109
, −10
109
, 0,3; 10
109
, −3
109
, −31
3
. 111. б) 8. 112. 129°; 21°; 30°.
113. а) 51 см; б) 68 см; в) 42,5 см. 114. 4 см, 6 см, 8 см, или 7,2 см, 10,8 см,
14,4 см, или 36 см, 54 см, 72 см. 115. 2 3.
Раздел 2
121. 100°; 260°. 124. 90°. 127. а) 59°; б) 65°; в) 72°; г) 36°. 130. а) 75°, 105°,
65°; б) 75°, 105°, 65°; в) 50°, 224°, 30°; г) 100°, 40°, 105°; д) 125°, 220°, 10°;
е) 116°, 134°, 26°. 131. а) 30°, 195°; б) 94°, 162°; в) 50°, 166°; г) 7°30′, 100°.
132. 50°, 63°, 73°. 133. 40°, 47°, 141°. 134. а) 100°; б) 47°; в) 60°; г) 36°;
д) 60°; е) 45°. 136. 120°; 240°. 137. б) 2α; 180° 2α. 140. а) l
3
; б)
l m
m
2 2
4
8
+
.
141. б) sin2
α; в) 45°; г) 2α, 180° 4α, 2α; д) 30°. 142. а) 120°; б) 24 3 см.
143. а) 122°; б) 315 дм. 148. а) 2, 6; б) 4; в) 2; г) нет корней.
149. а) 5, 2 5; б) 5; 1. 151. p q. 152. 15 м2
. 154. 18 2 3+ .
155. 36° и 264°. 168. а) 90°, 45°, 45°; π
2
, π
4
, π
4
; б) 90°, 36°, 54°; π
2
, π
5
, 3
10
π;
в) 90°, 45°, 45°; π
2
, π
4
, π
4
; г) 40°, 70°, 90°, 160°; 2
9
π, 7
18
π, π
2
, 8
9
π; д) 60°,
120°, 75°, 105°; π
3
, 2
3
π, 5
12
π, 7
12
π; е) 80°, 100°, 100°, 80°; 4
9
π, 5
9
π, 5
9
π, 4
9
π;
Правообладатель Народная асвета
Народная
асвета

83. 383
ж) 90°, 90°, 75°, 105°; π
2
, π
2
, 5
12
π, 7
12
π; з) 15°, 165°, 15°, 165°; π
12
,
11
12
π, π
12
, 11
12
π. 169. а) 3π 1
с
; б) 10π 1
с
; в) 22π 1
с
; г) 331
3
π 1
с
.
170. а) 7200π 1
ч
; б) 2π 1
ч
; в) π
6
1
ч
. 173. 11°15′; π
16
. 178. а) 5; б) 1,5;
в) 2π; г) 3,05. 180. а) 29,4 см2
; б) 132,47 см2
; в) 282,6 см2
; г) 103,5 см2
.
181. а) 30 м2
; б) 100 м2
; в) 239 м2
; г) 492 м2
. 182. б) 64
3π
м; г) 160
46
м,
или 23,59 м. 183. в)
5 5
2π
м, или 4,46 м. 190. а) Нет корней; б) 1,5;
в) 3,25; 0,75; г) 12
3
; 52
3
. 191. а) Нет решений; б) ( ; 1,5) ∪ (1,5; );
в) ( ; 3,25] ∪ [0,75; ); г) 12
3
52
3
; . 193. 130 см. 194. 90 м. 195. 104 см.
196. а) r2
4
(4π 3 3 3 ); б) r
2
(1 3 ); в) 15°. 201. 2 см. 208. 122°,
26°, 32°. 214. а) 35°, 125°; б) 120°, 30°; в) 25°, 115°, 40°. 215. 90°, 45°, 45°,
12 см, 12 см, 12 2 см. 216. 100°, 40°, 40°. 217. 80°, 60°, 40°. 219. а) 40; б) 120;
в) 1 2 1 4, , ; г) 2,5. 220. 24. 221. а) 15; б) 16. 222. а) 22 см; б) 193 см.
223. а) 4 см, 14 см; б) 10 см, 12 см. 231. а) Нет решений; б) ( ; 0,25);
в) нет решений; г) 1
15
; .+ 232. а) 33,6 см и 36,4 см; б) 28 8
9
см и 311
9
см.
234. а) 5 км/ч и 6 км/ч; б)
241 1
4
−
км/ч, или 3,63 км/ч, и
241 3
4
+
км/ч,
или 4,63 км/ч. 242. а) 20 см; б) 8 2 см; в) 106°; г) 13,44 м; д) 146° 26′ 34″.
244. 125°, 120°, 115°. 246. 110°. 247. 160°. 248. k c. 249. 3; 17; 17; 7; 7; 3.
250.
a b c+ +
2
,
a b c+ −
2
,
a b c− +
2
. 251. 25. 252. 40 м. 253. а) 600 мм;
б) 400 мм. 254. а) 102 мм; б) 27 см. 256. 10 м. 257. 4,8; 919
30
. 259. а) 70°, 20°,
90°; б) 56°, 34°, 90°. 260. а) 63°, 54°, 63°; б) 65°, 50°, 65°. 262. d, d cos β, d sin β.
263. а) 30,5; б) 10 или 10
3
; в) 12,3. 264. 12 3. 265. а) 3; б) 3
3
.
266. R a 3
3
. 267. 48. 271. BOC AOC AOB. 274. 2R sin α
2
, 2R sin
β
2
,
2R sin
γ
2
. 275. а)
m n m n+ +− 2 2
2
; б) k
2
(cos α sin α 1); в) 5
2sin α
(cos α
sin α 1); г)
P sin cos
sin cos
.
α α
α α
+ −( )
+ +( )
1
2 1
276. а) asin
sin
;α
α2 1
2
+
б)
a b a
b a
4
2 2
2 2
−
+( )
;
Правообладатель Народная асвета
Народная
асвета

84. 384
в)
acos
sin
;
α
α
2
2 1
2
+
г)
hsin sin
cos
;
β β
β
2
2 1 +( )
д)
2
2 1
2
Ssin
sin
;
α
α+
е)
Psin
cos
;
2
4 1
2
β
β+( )
ж)
Rsin cos
sin
;
α α
α
2
1
2
+
з)
h h h
h
2 1 2
1
2
4
−( )
. 279. 20°. 280. а) 24°, 150°; б) 113°, 76°;
в) 11°, 160°; г) 5°, 85°. 281. а) 3; б) 2; в) 1; г) 1. 283. а) [ 1,2; ); б) ( ; ).
288. 240 мм. 289. а) 30 мм; б) 56 см; в) 18 м; г) 61 дм. 291. а) 13 см или
21 см; б) 180 см или 212 см. 293. 120 см, 153 см. 298. 132 см. 299. 12 см,
18 см, 10 см, 16 см. 301. 120. 303. а) 4; 6; б) 8; 12; в) 9; 25; г) 18; 32.
304. 7 и 21. 310. а) 1
2
a sin α; б) mn
m n+
sin β. 312. 26 см. 313. а) 2R2
; б) 2R2
.
314. б) a d a2 2
− ; в) (0; 0,5d2
]. 319. 30°. 320. а) 5 5
2
; б) 5 2
2
; в) 13 2
2
;
г) 8 1
8
. 321. c
c ab
c a b
2
2 2
4
+
( )− −
. 322. а) cos C l
k
1; 2k l; б) 60°;
в) MN u v; NP 2u; MQ t v; sin Q
2u
t v+
. 327. lm
k
, ln
k
. 330. 75 см2
.
331. 1736 3 м2
;
3472 3
241
м. 332. а) ( 35
7
; ∞); б) ( ∞; 6]; в) [ 5; 0];
г) ( ∞; 8). 335. На 86 2
3
увеличилось. 336. За 30 дней.
Раздел 3
350. а) ( ∞; 1,5) ∪ (1,5; ∞); в) ( ∞; 1) ∪ (2; ∞); г) ( 4; 1); д) нет
решений; е) ( ∞; ∞); ж) ( ∞; ∞); з) 3. 351. а) ( ∞; 5) ∪ (9; ∞);
в) ( ∞; 6) ∪ ( 5; ∞); ж) нет решений. 352. а) − −; 1
3
∪ (2; ∞);
в) − 2
3
3; ; е) a 1, a 3. 353. г) y 1; ж) ( ∞; 1] ∪ [4; ∞); з) [ 5; 2]; к) v 0, v 7,
v 2,5. 355. а) [ 2; 1]; б) − −; 1
3
∪ 2
3
; .+ 356. б) Функция не оп-
ределена ни в одной точке; в) ( ∞; ∞); г) s 2. 361. а) a 9 и h a 1.
362. а) a 1 и a 3. 363. Не меньше 16 км/ч. 367. 18 м. 369. 35 4 2+ см.
370. а) 18 см, 7 3 см2
; б) 20 8
3
дм, 20
3
дм2
; в) 12 4 2 м, 12 м2
;
г) 130 100
3
мм, 1625
3
мм2
. 371. 20 см и 30 см. 375. а) (4; ∞); б) нет
решений; в) (2; 4); г) ( ∞; 5); д) нет решений; е) (4; ∞). 376. а) Нет
решений; б) [2; 4); в) (3; 5); г) нет решений; д) нет решений; е) 3. 377.
а) (2; 3); б) ( ∞; 2] ∪ [3; 4); в) нет решений; г) [ 5; 4] ∪ [3; ∞);
Правообладатель Народная асвета
Народная
асвета

85. 385
д) ( ∞; 0,5] ∪ [2; 3]; е) [ 3; 2]. 378. а) ( 4; 3) ∪ ( 2; 2); б) [ 5; 3] ∪ [1; 2];
в) ( ∞; 2] ∪ [7; ∞); г) ( 4,5; 3]; д) [ 2,5; 1]; е) − −; 1
3
∪ (4; ∞).
379. а) ( ∞; 1); б) 1
3
1; ; в) нет решений; г) ( ∞; 2); д) (2; ∞);
е) ( 1; 0,5) ∪ 4
5
13
7
; . 380. а) Нет решений; б) ( ∞; 2) ∪ − 3
4
1
2
; ;
в) ( ∞; 2) ∪ (1; 3); г) ( ∞; 1); д) (2; ∞); е) нет решений. 381. а) ( ∞; 3) ∪
∪ (5; ∞); б) [ 3; 5]; в) ( 3; 5); г) ( ∞; 3] ∪ [5; ∞); д) ( ∞; 3) ∪
∪ ( 3; 5) ∪ (5; ∞); е) ( ∞; 3) ∪ (5; ∞). 382. а) ( ∞; 3) ∪ (5; ∞); б) ( 4; 1];
в) ( ∞; 7) ∪ [ 3; ∞); г) − −∞; 10
3
∪ (2; ∞); д) ( 2; 3); е) − ; 1
3
∪
∪ (0,75; ∞); ж) ( 1; 0,5) ∪ (2; ∞); з) ( ∞; 2) ∪ [ 1; 3]; и) (0,5; 1) ∪
∪ (2; ∞). 383. а) ( ∞; 2,5) ∪ (3; ∞); д) −3 1
3
; ; ж) ( 0,6; 1).
384. а) ( ∞; 3) ∪ − −3
5
1
3
; ; б) ( ∞; 1] ∪ − 1
3
1
3
; . 385. а) (0; 1]; б) [0; ∞);
в) ( 1; 2); г) (1; 4). 386. а) ( 1; 2]; б) ( ∞; 2) ∪ [7; ∞); в) [ 5; 1]; г) нет
решений. 387. а) ( 1,5; 1) ∪ 0 1
2
; ; б) ( 1; 0) ∪ (6; 7); в) ( 1; 1) ∪ (2; 4);
г) (1; 7). 388. а) ( ; 1) ∪ (3; 4] ∪ [7; ); б) [0; 0,5]; в) нет решений;
г) [1; 6]. 389. а) g 6; б) 3
2
; в) [ 3; 2] ∪ [2; 3]; г) − −; 5 ∪ 5; .+
390. а) ( ∞; 1) ∪ ( 1; 0) ∪ (0; 2) ∪ (2; ∞); б) ( ∞; 2) ∪ 2 21
3
; ∪ 21
3
; ;+
в) ( ∞; 2) ∪ (2; 4) ∪ (4; ∞); г) ( ∞; 1) ∪ (1; ∞). 391. а) ( 4; 5) ∪
∪ (9; ∞); б) ( ∞; 4] ∪ [5; 10]; в) ( ∞; 4) ∪ (1; 9); г) [ 4; 0] ∪ [9; ∞);
д) ( ∞; 3) ∪ ( 3; 1) ∪ ( 1; 4) ∪ (4; ∞); е) ( 8; 5) ∪ ( 1; ∞).
392. а) ( ∞; 3] ∪ (1; 2]; б) [1; 3) ∪ (5; ∞); в) ( 6; 4) ∪ (7; ∞); г) ( ∞; 3] ∪
∪ [2; ∞); д) { 8} ∪ ( 5; 1]; е) 4. 393. а) Нет решений; б) ( ∞; 0,5) ∪
∪ (1; ∞); в) ( ∞; 3) ∪ (0; 1) ∪ (3; ∞); г) − −; 2
3
∪ (0; 0,5) ∪ 2
3
; ;+
д) ( ∞; 2) ∪ (2; 3); е) [ 3; 1,5) ∪ (3; ∞). 394. а) − −; 6 ∪ (0; 2) ∪
∪ 6; ;+ б) − −; 2 ∪ 2 5 2; ; в) ( 1; 1) ∪ (1; 8]; г) − −15 3; ∪
∪ 0 15; ; д) − −; 3 ∪ − 3
2
3; ; е) ( ∞; 4) ∪ ( 1; 1) ∪ (1; ∞).
395. а) ( 3; 1); б) ( ∞; 3) ∪ ( 1; 2) ∪ (2; 4) ∪ (4; ∞); в) 3; 1; 2; 4.
396. а) (6; ∞); б) [ 1; 6]; в) ( ∞; 1) ∪ ( 1; 6) ∪ (6; ∞); г) { 1} ∪ [6; ∞);
д) ( ∞; 1); е) [ 1; ∞). 397. а) ( ∞; 3) ∪ (2; 3) ∪ (7; ∞); б) [ 4; 3] ∪
∪ {4}; в) (4; 7); г) [ 6; 0] ∪ [6; ∞); д) нет решений; е) ( ∞; 2) ∪
∪ − 2 2; ∪ (2; ∞). 398. { 7} ∪ [ 3; 9]. 399. 0;
7 33
8
. 400. ( 5; ∞).
Правообладатель Народная асвета
Народная
асвета

86. 386
401. (0; 1,2). 402. x1 > 0 и x2 0 при любом значении c. 403. Ни при каких.
404.
− − +5 2 43
3
5 2 43
3
−
; . 407. а) 3
2
1; б) 0; в) 3 3; г) 1.
408. а) cos2
β; б) 1
2
cos
;
β
в) 1; г) sin ω cos ω. 409. 47°. 410. 18°, 36°, 54°,
72°, 90°. 411. 7,5. 412. 120°,
8932
631
3
м.
Раздел 4
416. 2. 417. 9 2 6 3 3 6. 420. а) 133 м; 51°23′12″; 8°36′48″;
б) 1380 3 м2
; в) 23 3 м; 2760 3
133
м; 120 3 м; г) 19 43
143
м. 421. а) 10 3
3
;
б) m
2sin
;
α β+( )
в) ab
h2
. 424. а) 7; б) 13; в) 5; г) 13. 429. AC 8, BC 10
или AC 8, BC 2,8. 430. а) 2 3 6 2; б) 8 3
3
; в) 6 3 6 или
6 3 10. 431. 12, 6 2 3 1− , 12 3 1− ; 6 2, 6 3 1− . 433. b
h
2
2
,
h a
h2 8
2
+ , 2
4
2
2 2
b
b a−
. 434. а) 5 13
4
; б) 130
3
. 435. 1 3 61, . 436.
c cos
cos
,
ϕ
ϕ
2
csin
cos
,
ϕ
ϕ
45
2
° −
csin cos
cos
.
ϕ ϕ
ϕ135°( )−
440. a 10
4
. 441. а)
2 3 1
4
−( ); б)
2 3 1
4
+( ).
442.
asin
sin
;
β
γ
β +
2
asin
sin
;
γ
γ
β
+
2
asin sin
sin sin cos
.
β γ
β γ
β γ
+( )
+
2
445. a 3
2
. 446. а) 60°;
б) 120°. 448. 5 106; 331
3
. 452. а) 3
2 60sin sin
;
α α+ ° +( )( )
б) 3
3
. 461. 135.
462. 15 т. 463. 9 кг. 464. 7 дней, 12 дней. 472. а) 1
2
; б) 1
4
; в) 3
4
; г) 7
8
;
д) 3
4
; е) 1
2
; ж) 1
4
; з) 4
9
. 476. а) 2
3
. 480. а) a2
4
, 3
4
2
a ; б) 2
9
2
a , 7
9
2
a ;
в) 6
25
2
a , 19
25
2
a . 490. а) 1 3; б) 1 2; в) 1 4; г) 1 4. 491. а) S; б) S; в) 2S;
г) 7S. 493. а) 1
2
; б) 1
5
; в) 4
5
; г) 1
5
. 494. а) x
2
(a b x); б) 1
2
(ay bx xy);
в) 0,094ab. 496. 900. 500. а) 1
2
; б) 1
4
; в) 1
2
; г) 1
2
. 501. а) 84 см2
; б) 173,6 см2
.
504. S1 S3 S2. 506. kl
m
. 510.
a b2 2
2
+
. 512. 1
4
. 513. 2
7
. 514. 5
4
. 515. 11
12
.
516. 1
5
. 523. 600 или 100 4 2+( ). 529. а) ( 3; 1) ∪ (4; ∞); б) [ 5; 2) ∪ (1; 2];
в) ( ∞; 1) ∪ − 1
2
2 2
3
; ∪ (3; ∞); г) ( ∞; 1) ∪ − 1
4
1
3
; ∪ [2; ∞);
Правообладатель Народная асвета
Народная
асвета

87. 387
д) ( ∞; 2) ∪ (2; 6); е) ( ∞; 3) ∪ [ 1; 2) ∪ [4; ∞); ж) ( 2; 1) ∪ (0,5;
0,75); з) − −1
3
1
5
; ∪ (1; 2]. 530. а) 2; 16; 24; б) 4; 4; 23; в) 3; 36; 96;
г) 2; 8; 15. 531. а) a 2; b 3; б) a 1; c 9; в) b 4; c 1.
Раздел 5
537. а) 0; 3; в) 0; д) 1; ж) 1
3
; з) 1
2
; и) 2; 2
2
; к) 1; 4; л) 1; 2;
м) 2; 3. 538. а) 1; 5; б) 1; 1
2
; в) 2; 6; г) 2; 1
2
; д) 3;
е) нет корней; и) 46 2− ; к) 1; л) 4; 3
4
; м) 1
3
; 1
5
. 540. а) х4
11х2
18 0; б) y4
26y2
36 0. 541. а) (x 2)(x 2) x −( )2 2 x +( )2 2 ;
б ) s −( )2 2 s +( )2 2 s −( )2 3 s +( )2 3 ; в ) ( 2 5 w 2
1 ) w −( )3 w +( )3 ;
г) (4y2
9)(4y 1)(4y 1); д) m −( )2 m +( )2 m −( )30 m +( )30 ;
е) (6z2
5)(5z2
6). 542. а) 1; б) 4; m; в) m; n; г) m
n
; n
m
;
д) 1; ± mn; е) ± m; ± n. 543. (x a)(x a)(x a 1)(x a 1).
544. а)
a
a
2
2
3
9
−
−
; б)
t a
t
2 2
2
1
+
+
; в)
x n
x n
2 2
2 2
2−
−
; г)
4 2 2
2 2
z p
z p
−
−
. 545. а) 3; ± 3;
б) 3; ± 10; в) 2 ± 3; г) 4; 2; − ±1 2 2. 547. а) q 3; б) q 4; в) q 7;
г) q 5. 549. а) 1; ± − ±3 15 ; б) 2; ± 6; в) 5; 2,5; 1,25; −12
3
; г) 0,5.
550. 4. 551. R
R a
2
2 2
4 −
. 552. а) 2; 3; б) 1; 2
3
; в)
3 17
2
±
; г) 2,5; 1; д) 2; 2
5
;
е) 0,5; 5,5. 553. а) 1; 5; б) 3; в) ± −( )2 1 ; г) 1; д) 1;
е) 1; 6; ж) 3; 1; 5; 7; з) 1,5; 4,5; и) 8,5; 0,5; 1,5; 9,5; к) 0; 7; л) 0;
11
3
; м) 5; 9; н) 3; − 5
6
; − 1
2
; 12
3
; о) 1; 3; п) 2; 4. 554. а) 10; 16; б) 2;
1; 0; в) 2; − ±3 5; г) 6; 4;
− ±15 129
2
; д) 4; 2; е) 0,5; 3,5; ж) 2; 1;
з) нет корней; и) 3,5; 3; к) 2; 3;
5 89
2
±
; л) 2; 1
2
; 3; 1
3
; м) 2; 0.
555.а)0,25;б) − ±1 5; в) 1;2;г) 2; 1; 2 2± ; д)1;е)1;ж) − ±1 2; з) 1 19± ;
и)
− ±11 105
4
; к) 1; л) 3; 2; м) 2; 3
4
. 556. а) 3; 1; б) − ±3 15; в) 7; 1
7
;
г) 0; 1; д) 3; е) 1; 2; ж) 2; з) 2; 1; 2; 4. 557. а) 1; б) 21
2
; в)
− ±3 5
2
;
г)
− ±3 5
2
;
− ±7 33
4
; д) 1 3 3 2 3+ ; е) 51
5
; ж) ± −1 3
7
21
3
; ; ;
Правообладатель Народная асвета
Народная
асвета

88. 388
з) 1. 558. а) 3
2
; 2
3
; б)
− ±5 21
2
; в) 3 2 2; 2 3; г) 1;
2; 1
2
; д) 1;
13 313
12
±
; е) 3; − 1
3
; − 5
2
; 2
5
; ж)
− ±3 5
2
; з) 2 5;
1 17
4
±
. 559. а) 27; б) 18; в) 10 7
11
; г) 1212
17
. 565. а) 3; б) 9; в) 5; г) 34.
566. а) 217 см, 3°53′25″, 56°6′35″; б) 884 3 см2
, 1768 3
217
см, 104 3 см,
221 3
26
см. 567. а) 5 3 1−( ); б) 5
2
6 1 3 1+( ) −( ). 568. 47 ц/га, 49 ц/га.
569. 51 ц/га, 45 ц/га. 570. 48 ц/га. 583. а) 5; б) 7; в) 3. 589. а) 3x 4y 1 0;
б) x y 8 0; в) x y 2 0; г) 2x y 0; д) y 1 0; е) x 5 0.
590. а) (5; 0); б) (0; 2). 591. а) y 7; б) x 2. 592. а) 5; б) 3,5; в) 2; г) 3;
д) 28,5. 598. а) x2
y2
20; б) x2
(y 7)2
5. 599. а) (x 2)2
(y 2)2
50;
б) (x 3)2
(y 1)2
17. 602. а) ( 5; 0) ∪ (5; ∞); ж) ( ∞; 4) ∪ (1; ∞);
з) [ 2; 3]. 603. а) ( ∞; 1) ∪ (2; 3); б) (2; 3) ∪ (5; ∞); в) ( ∞; 3) ∪ ( 2; 1) ∪
∪ (4; ∞); г) ( 4; 1) ∪ ( 1; 6). 605. а) 4
3
; б) −16
7
; в) 1 3
17
; г) 11
3
.
606. 15 см. 607. 504 см2
. 616. (11; 8) и ( 15; 18). 620. а) (2,25; 3,5);
б) (2; 4); в) ( 1; 3); г) (3; 2). 624. а) ( 1; 3); б) (1; 2); в) (64; 56); г) ( 2; 3).
625. а) (0,25; 0); б) ( 0,6; 2); в) − 1
3
1
2
; ; г) (2; 1); д) 1
2
1
3
; ;− е) (6; 7).
626. а) y x 5; б) y 23
34
x 1 9
34
; в) y − 1
3
x 31
3
; г) y 3x 29.
627. а) x y
−
+
5 11
1; б) x y
4 7
+
−
1. 628. а) ( 1; 3); б) ( 1; 1); в) ( 2; 2);
г) (11; 1). 629. а) (3; 2); б) (3; 1); в) (7; 3); г) (1; 1). 630. а) (5; 2); б) (1; 2);
в) (4; 2); г) (4,5; 7); д) ( 3; 23); е) (7; 4,5). 631. а) ( 4; 3); б) ( 2; 7);
в) ( 10; 5); г) ( 11; 4). 632. а) (25; 5); б) (5; 30); в) ( 5; 30); г) ( 5;
30). 633. а) (6; 9); б) (6; 6); в) (24; 12); г) 78
19
60
19
; . 635. а) (1; 2);
б) (3; 2); в) (3; 2); г) ( 6; 0). 636. а) (5; 8); б) (5; 11); в) (4; 3); г) (4; 6).
639. а) −1 3
11
2 3
5
; ; б) (2,7; ). 643. а) 3; б) 1
3
. 644. За 20 дней
и 30 дней. 645. За 12 ч и за 8 ч. 646. 4 1. 647. 35 ч. 649. 2
3
км. 657. а) (3; 1),
(5; 3); б) ( 7; 3), 3 1
3
; ; в) (10; 1,8); г) (2; 1), ( 1,5; 6). 658. а) ( 1; 1),
18
7
9
14
; ; б) (3; 1), (1; 3); в) (3; 2), ( 2; 3); г) (2; 3), − −1
3
5
3
; .
659. а) ( 10; 15), (3; 2); б) (3; 2), (2; 3), ( 2; 3), ( 3; 2); в) (2; 3),
Правообладатель Народная асвета
Народная
асвета

89. 389
(3; 2); г)
− + +5 15
2
5 15
2
; ,
−5 15
2
5 15
2
− −
; , 2 6 2 6+ − +( ); ,
2 6 2 6− − −( ); . 660. а) (4; 6), (6; 4); б) (10; 4), ( 4; 10); в) (1; 5), (5; 1);
г) нет решений. 661. а) (3; 4), (4; 3), ( 4; 3), ( 3; 4); б) (5; 3), ( 5; 3);
в) (3; 1), ( 3; 1); г) (4; 2), ( 4; 2), 2
13
16
13
; , − −2
13
16
13
; .
662. а) (2; 0,1); б) 1
3
1
4
; ; в) (4,8; 24); г) ( 2; 5). 663. а) 14 1
3
29; ; б) [ 12;
16,5]; в) ( 3; 8]; г) ( 2,3; 16). 664. а) ( ∞; 1) ∪ (0; 3); б) ( 2; 0) ∪ (6; ∞);
в) (2 5; 0) ∪ (2 5; ∞); г) ( ∞; 0] ∪ (1; 4]. 665. а) ( ∞; 1,5) ∪ ( 1; 1) ∪
∪ (4; 6); б) ( ∞; 3) ∪ 2
3
1;⎡
⎣⎢
⎞
⎠
⎟ в) ( 5; 0,5) ∪ (2; 3) ∪ (3; ∞); г) −⎡
⎣⎢
⎤
⎦⎥
3
7
1; ∪ {3} ∪
∪ (5; ∞). 668. 4 ч, 5 ч. 670. 20 %. 671. За 2 ч 30 мин, за 2 ч 40 мин.
676. 2,7 м; 1,6 м. 677. 24 ц/га; 28 ц/га. 678. 195; 238. 680. 22 км/ч.
681. 67; 11. 682. 7
13
. 683. 17
23
. 684. 90; 162. 685. 50 га, 45 га. 686. а) 42 ц/га;
49 ц/га; б) 36 га; 35 га. 687. 6 км/ч, 1 км/ч. 688. 37. 689. 1200 р., 1500 р.
690. 2500; 3125. 691. 3 кг; 7 кг. 692. 54 км/ч, 6 ч. 693. 56 ч, 42 ч. 694. 39 м,
26 м. 695. а) ( ∞; 2 2 ) ∪ ( 2 2; 1); б) ( ∞; 1) ∪ 2
3
1; ; в) (4; ∞);
г) ( 4; 3) ∪ ( 2; 1) ∪ (0; 1). 696. а) ( ∞; 3) ∪ (1; 7) ∪ (7; ∞); б) ( ∞; 4) ∪
∪ {5; 10}; в) ( ∞; 4) ∪ ( 4; 1); г) ( ∞; 4] ∪ {0} ∪ [9; ∞); д) нет решений;
е) ( 8; 5) ∪ ( 1; ∞). 697. а) x y 1; б) 2x y 8; в) x 8y 26 0.
698. 4 см или 6 см. 699. 120 км. 700. В 2,5 раза. 701. В 11 ч 40 мин.
702. 8376 тыс., 4620 тыс., 1397 тыс., 1346 тыс., 1260 тыс. 703. 35 см2
.
Раздел 6
718. а) 4; б) 11; в) 32; г) 101. 719. а) 4; б) 9. 753. а) ( 16; 11), (8; 5);
б) 16
3
3; ; в) (5; 1), − −5
7
11
29
; ; г) 2 1 2; ,+( ) −( )2 1 2; .− 754. 77 и 91.
755. 150, 225 и 375. 756. 15 дет./день. 757. 14. 758. 3,2 ч, 1,6 ч. 780. а) 0,1;
б) 1,02. 785. 3(n m). 786. 100. 787. а) 21; 525; б) 12; 408. 788. а) 2;
4,25; б) 7; 5. 789. а) 2; 22; б) 10; 18. 790. а) 17; 61; б) 23; 58. 791. а) 8; 23;
б) 12; 63. 792. а) 20 100; б) n(n 1); в) n2
; г) 123 300. 794. а) 2485; б) 494 550;
в) 6400; г) 7 071 071; д) 445 500; е) 339 769. 795. Через минуту. 796. а) 15;
б) 465. 797. 50 м/мин2
. 798. 203,5 см. 799. а) ≈ 4 с; б) ≈ 122 м. 800. 1275.
801. 1160. 803. а) 6; б) 2; в) 6,5; г) 8 5 3. 806. а) − 3
4
; − 1
4
; 1
4
; 3
4
;
Правообладатель Народная асвета
Народная
асвета

90. 390
б) 5; 4. 810. 15 300. 811. 2 и 3 или 8 и 3. 812. 5 и 5 или 5 и 5. 815. а) (5; 0),
( 5; 10); б) (2; 4), ( 10; 20). 817. а) (5; 2); б) ( 3; 2), (2; 3); в) (1; 3), ( 3; 1);
г) ( 3; 5), (5; 3). 818. а) [0,5; 2,5); б) ( ∞; 2) ∪ − −2 1
3
; ∪ (1; ∞);
в) ( 7; 4] ∪ {0} ∪ [6; ∞); г) ( 3; 2) ∪ − 1
3
2; . 819. 20 см. 820. 55.
821. 672. 822. 300 и 500. 838. а) a1 1, q 3; б) a1
1
2
, q − 1
2
.
856. 17; 10; 3 или 8; 10; 12. 857. 18 м, 6 м, 2 м. 858. а) 128; 7; б) 567; 5;
в) 3; 384; г) 0,5; 5. 864. а) x3
1; б) a6
1. 865. а) 1
1 15
( )( )
;
a a− +
б) (t 1)(t7
1); в) 1
1x +
; г) 1
1 16 5 4 3 3
( )( )
.
b b b b b b b+ + + + + + +
866. а) a10
a5
1; б) y14
y7
1. 867. а) 4; 10; 16 или 16; 10; 4; б) 3; 15; 75
или 75; 15; 3. 872. а) 3; 2; б) 5; 2 или 5; 2. 873. а) 3; 2; 10; б) 1; 2; 7.
874. 40. 875. 765. 876. 2. 877. 9; 6; 4; 2 2
3
. 878. b1 8; q 1,5.
880. а) b1 1, q 3 или b1 9, q 1
38
; б) b1 1, q 3 или b1 9, q 1
3
.
881. а) 27; 19; 11 или 12; 19; 26; б) 4; 8; 16 или 16; 8; 4; в) 2; 8; 32.
882. 128 7
8
или32,5.883.22,5или2,5.884.10.885.4.886.6.887.a1 27,d 9.
888. а) (r 1)2
(r 1)(r2
r 1); б) p(p 1)2
(p 1)(p2
1); в) r2
(r 1)2
×
× (r2
r 1); г) (jh jf gh gf)(jh gh gf jf); д) (f g h)( f g h) ×
× (f g – h)( f g h); е) (a y t)(a – y t)(a y t)( a y t); ж) (y c)3
×
× (y c); з) 2z(z 1)2
(z 1); и) (p 1)2
(p 1)3
. 889. а) 0; б)
4 1
3
n
n
−( )
; в) x
x2
1+
;
г)
n m
mn
−
1 +
. 890. а) 2
7
1; ; б) ( 1; ); в) (0; 0,5); г) ( ; 2,5) ∪ (0,4; );
д) ( ; 2) ∪ (3; 8); е) ( 3; 0) ∪ (1; ); ж) ( ; 3) ∪ ( 1,75; 2);
з) ( 3; 0,5) ∪ 5
3
; .+ 891. а) (2; ∞); б) − −; 11
3
∪ {1; 2};
в) − −; 2
3
∪ − 2
3
1
2
; ; г) − −; 11
3
∪ 3
4
1
3
; ; д) нет решений;
е) −11
3
1
6
; ∪(2; ).893.90° α
2
. 894.
a b
a b
a b
−
+
+2 2
. 895.(6 π) 2π (6 π).
896. a2
8
2 1 2 2 1−( ) −( )( )π − 4 . 897. 8 см; 14 см. 898. 2,4 кг, 1,6 кг.
Раздел 7
913. а)
a3
3
,
a3
2 3
; б)
a4 2
2
,
a4
2
; в) a6,
a6 3
2
; г)
a5
2 36sin
,
°
0,5a5 ctg 36°.
925. а) 144 см2
; б) 64 3 м2
; в) 648 3 дм2
; г) 82,84 м2
. 926. 3 4.
Правообладатель Народная асвета
Народная
асвета

91. 391
929. 2 6 м. 932.
R r
r
1 2
1
. 934. а) 30°, 60°; б) 60°; в) 3; г) 1 3; д) 1 2; е) 18.
943. а) ( ; 1) ∪ (1; 2) ∪ (3; ); б) ( 4; 2) ∪ (3; ); в) [3; 4]; г) [ 3; 1] ∪
∪ [4; 5]; д) ( 1; 2); е) ( 5; 3) ∪ ( 3; 2). 944. а) 1
3
; б) [1; ∞); в) 0; 1; г) 3; 4;
д) 0; 1; 3; 4; е) − − − +⎡
⎣
⎤
⎦2 2 2 2; . 945. b
a
1. 946. a2
4
6 3 6− −( )π .
947. 150 м, 125 м. 948. 27, 36, 63. 953. 57 м. 958. а) 12π см; б) 4π 3 см;
в) 36π см или 12π 3 см; г) 60π см. 959. а) πc; б) π
α
a
sin
; в) π
β
a
sin
2
или π
β
a
cos
2
;
г) π
γ
d
sin
. 960. а) 30,8 см; б) 14,7 см; в) 29,0 см. 961. а)
π δ δ
δ
b sin cos
sin
;
+ −( )1
б) 2πh tg
ϕ
2
ctg ϕ; в) πcd
c d2 2
+
; г) πl. 965.
r
r
n1
2
. 966.
r
r
n3
1
. 972. 1
2
+ H
R
.
973. πR
3
, 5
3
πR . 975. 180°
π
. 976. а) R 3; б) R; в) 2R sin80°. 977. а) 8
3
πr ;
б) 4πr; в) 10
3
πr . 978. 2
3
πa. 979.
πa tg ω
2
180°
(180° ω),
πa tg ω
2
180°
(180° ω).
980. 24
11
πl. 984. 36 см. 985. 25 см. 986. 5,7°. 992. 4 3. 993. 300.
994. 2 1πR l
r
−
π
. 997. а) R
3
3 3−( ); б) R 2 1−( ); в) R
3
. 998. а) R 3 2 2+( );
б) R 3 2 2+( ); в) R. 999. а) 16 15
16 16
z
z c−
; б) 4
4s s +( )
; в) 1; г) d f g.
1000. а) ( 8; 1); б) ( 1; 0,4]; в) (0,5; 2]; г) ( 5; 2) ∪ ( 2; 2); д) ( ; 4) ∪
∪ ( 4; 1,5) ∪ (4; ); е) ( 5; 0,25) ∪ 2
3
7; . 1001. а) ( 4; 1) ∪ 2
3
2 5; , ;
е) ( ∞; 4) ∪ ( 4; 1) ∪ 2
3
2 5; , . 1003. R2
2 3
3
2
π + . 1004.
b a2 2
2
−
.
1014. а) 12π; б) π
α
a2
2
4cos
; в)
π 4
64
2 2 2
2
h c
h
+( ) ; г) 700
3
π; д) 25
2
π
β γsin
.
+( )
1015. а) 3
4
π; б)
π ϕ ϕ
ϕ ϕ
c2 2 2
2
1
sin cos
sin cos
;
+ +( )
в)
π −h a h
a a h
2 2 2
2 2
2
( )
+ −( )
; г) 525π; д) 400π tg2 β
2
.
1019. 0,19. 1026. а)
ϕ
2
; б)
4
3 3
ϕ
; в) 2 3
9
π . 1028. πkl. 1033. a2
1
4
− π .
1034. R2
2
(2π πα sin α), R2
2
πα α− sin . 1035. 1
6
1
2π
. 1036. 1
4
1
2
−
π
1
6
1
4
+
π
1
6
1
2
+
π
1
6
1
4
+
π
1
4
1
2
−
π
.1037.(5π 3) (7π 3).1040. 13
6
π 3.
1042. π
3
1 3. 1043. а) 1; б) 2
2
; в) 1
2 36cos
;
°
г) 1
3
. 1045. 6 3 1−( ) π.
Правообладатель Народная асвета
Народная
асвета

92. 392
1046. а) 4x; б) 0; в) 4
4a a( )
;
+
г) 0. 1047. а) ± 2; б) ( ∞; 2) ∪ (0,25; 1] ∪
∪ [4; ∞); в) (0; 1). 1048. а) ( 4; 1) ∪ (1; 2); б) ( ∞; 1) ∪ (1; 2); в) {4} ∪
∪ [5; ∞); г) [1; 2] ∪ {3}; д) −⎡
⎣⎢
⎤
⎦⎥
1
3
1; ∪ {2}; е) − ; 1
3
∪ 1
3
2; ∪ (4; ∞);
ж) − −; 2
7
∪ {0} ∪ [1; ∞); з) [ 1; 0,2] ∪ {0; 2}. 1049. а) 2; б) 3.
1050. 6,25 см. 1051. 4
9
S. 1052. 90° α, 90° β, α β, если α 90° и β 90°;
α 90°, 180° β, 180° α β, если α > 90° и β 90°; 180° α, β 90°,
180° α β, если α 90° и β > 90°. 1053. 3 см × 3 см × 80 см; 4 см × 4 см × 30 см.
1054. 67 мм × 38 мм; 97 мм × 57 мм.
Раздел 8
1066. а) 4x 8; б) a4
b4
c4
2a2
b2
2a2
c2
2b2
c2
; в) 2l2
3kl 4jl 6jk;
г) 8fg 32fh 6g2
20gh 16h2
. 1068. а) (3e t)(2r 1); б) (3s d f)
(3s d f); в) (p 1)2
(p 1); г) (c 4)(c 3); д) 4qz; е) (a 1)2
(a2
a 1);
ж) (m 5n)(m 3n); з) (5g 2f)(2g 5f); и) (j h g)(j h g); к) (h 1)
(h 1)2
(h2
h 1); л) (3l 2k)(9l2
6lk 4k2
); м) (t c)(t c)(t2
tc c2
)
(t2
tc c2
). 1069. а) (x 5)(x2
x 25); б) (3y 2)(9y2
5y 4); в) (x 3)4
(x 6 3 3)(x 6 3 3);г) (a b)4
( ( ))a b− +2 3 ( ( )).a b− −2 3 1071.а)
l m
l m
+
−
;
б)
m n
m n
−
+
; в)
e r
r t
−
+
; г)
2 3
2 3
z y
z y
−
+
; д)
q r s
q r s
+ +
+ −
; е)
s f d
s f d
− +
+ −
; ж)
g j
j h
−
−
; з)
x z
y
+
−( )
;
1 2
и)
( )( )
( )( )
;
m m
n n
− +
− +
1 1
1 1
к)
p
p
−
−
7
5
. 1072. д)
m m
m
2
2
4 39
12 2
+ +
−( )
; е)
a
a
+
−
1
3
;
ж)
2 3
1 3 4
s
s s s
+
+ + −( )( )( )
; з)
20 1
2 1 2
d
d d
+
− +( )( )
. 1073. а) 0,25; б) 1 8
11
; в) 0,6;
г) 12
3
. 1074. а) 1
q
; б)
e
e
+
−
1
1
; в) 1; г)
2
2 2
fg
f g−
; д) 1
2
a2
a 1; е) z2
z 1;
ж)
10 3
7 2
q
q
+
+
; з)
p
p p
3
3
1− +
; и)
e e e
e e
( )
;
2
2
2 3
1
− +
+ +
к)
e k
ek
−
; л)
j h
j h
+
−
; м)
c
c
−
+
1
2 4( )
.
1075. а) 1; б)
m n
m n
2 2
2
+
+( )
; в) l(l k); г) d
d s( )
.
− 2
1076. 500
9
. 1077. а) 1,2 7;
б) ±2 3; в) −12
3
; г) 0,5. 1079. а) ( ∞; 1) ∪ (2; ∞); б) (0; 3);
в) − ; 1
3
∪ (4; ∞); г) ( ∞; 1) ∪ (6; ∞); д) ( ∞; 2) ∪
∪ (2; ∞); е) ( 6; 2); ж) ( ∞; 1,5) ∪ 2
3
; ;+ з) (1,6; 2) ∪ (2; 8).
Правообладатель Народная асвета
Народная
асвета

93. 393
1080. а) − −3
2
2
3
; ∪ (0,5; 2); б)
3 37
2
1
−
−; ∪
3 37
2
+
+; ;
в) 2 5 0 5−⎡⎣ ⎤⎦; , ∪ 2 2 5; ;+⎡⎣ ⎤⎦ г) −
+
−
+3 13
2
1 5
2
; ∪
13 3
2
5 1
2
− −
; ;
д) ( 1; 1) ∪ ( 2; 3); е) ( ∞; 2) ∪ ( 2; 1) ∪ − −1 3
4
; ∪ (5,5; ∞).
1081. а) (3; 2), ( 46; 51); б) (11; 7), 10 5
8
6 3
4
; ; в) 11
3
21
3
; ;
г) (4; 10), 2
11
1 5
11
; . 1082. а) 0; 1; б) 0; 1
2
. 1083.
a b+
2
.
1084. 1 17. 1085.
2 1
2
2 2
− + − +a b a b
. 1086. 1,6r. 1087.
a b
b
+
.
1088. 0 4 6, . 1089.
b a−
2
. 1091. 142,3 %. 1092. 92000 р., 9000 р.
1093. 86,1 ч. 1094. 6. 1095. x4
10x2
1 0. 1102. а) 720; б) 3 628 800;
в) 132; г) 13 49
91
. 1105. а) 6,25; б) 3,5; в) −1 2
11
; г) 125
126
. 1106. а) 9; б) 9,5;
в) 1 3
11
. 1124. а) 3; б) 9,492; в) 250. 1125. а) − 1
2z
; б) 1
d e+
; в) 2; г)
a + 2
2
.
1126. а) 2; б) 2
27
. 1127. а) 2; б) 7; в) 1; г) 3; д) 3; е) 3, ± 5
13
. 1128. а) 6 2
3
; ;
б) (3; 2); в) (4; 3); г) (11; 6). 1129. а)
− − − +3 21
2
3 21
2
; ; б) ( ∞; 7] ∪
∪ [1; ∞); в) [0,75; 7]; г)
− +7 109
6
7; . 1130. 648 (2 3 ). 1131. m2
3.
1132. c
3 3
2π
. 1134. 30°. 1135. 0,5ab. 1136. (a b)2
sin α
2
cos α
2
. 1138. 9 или 10.
1139. 184 см3
или 19 35
46
см3
. 1153. а) (p2
q2
)(p2
q2
3pq )(p2
q2
3pq); б)(m n)(m n)(m2
n2
mn)(m2
n2
mn). 1161. а) (s 1)2
(s 1);
б) (t 1)2
(t2
t 1); в) (d 1)(d 1)2
(d2
1); г) (e 3r)(e 4r); д) (zf f2
z2
)
(zf f2
z2
); е) (m2
n2
mn)(m2
n2
mn); ж) 4qd (q d)(q d); з) (sd rt
sr dt)(sd rt sr dt); и) (x 2k l)(x 4k l). 1162. а)
e t
e t
−
+
; б)
h g
f d
+
+
;
в) j g f; г) tr(t2
r2
); д) 1
1a +
; е)
( )
;
1 2
−
+
c
b p
ж)
z x
z x
−
+2
; з) 1
12
a a− +
.
1163. а) 2
1 + p
; б)
e
e
2
2
1
1
+
−
; в)
t y
t y
2 2
3 3
+
+
; г)
6
4
2
2 2
e
r e r−( )
; д)
p pq q
p q p q
2 2
2 2
+ +
+( ) +( )
;
е)
3 2 2
l k
l k
−
+
; ж)
2 43 2 3
2 2
j hj h
j h
+ +
+
; з)
2 2 2 2
( )
.
f g
g f
−
−
1164. а) 1; б) 12
19
; в) 1;
г) −31
6
. 1165. а) 2n; б) 1
ert
; в) 0; г) 0. 1167. а) 0; 3; б) 0; 2; в)
5 5
8
±
;
Правообладатель Народная асвета
Народная
асвета

94. 394
5 33
4
±
; г) 1; 2; 0,5. 1168. а) (2; 1), (4; 3); б) − −1 7
3
; , (1,5; 3,5);
в) (4; 0), ( 0,5; 4,5); г) (3; 2), 11
6
9
8
; . 1170. а) (1; 2), (2; 1); б) (12; 4),
(4; 12), ( 5 55; 5 55 ); в) (20; 15), ( 20; 15); г) (5; 2), 15
7
6
7
; .−
1171. а) ( 5; 0); б) − ; 1
3
∪ (1; ∞); в) ( ∞; 0,5] ∪ [2; ∞); г) [ 1,2; 0];
д) нет решений; е) ( ∞; ∞). 1172. а) ( 1; 5); б) ( ∞; 5) ∪ [3,5; ∞);
в) (1; 3] ∪ [4; 5); г) нет решений. 1175. 42 5; 56 5. 1177. h
2
1
2
1
2
−
+
sin
sin
.
α
α
1178. 90°. 1179. a
2
3 1+( ). 1181. 288. 1182. 2571 тыс., 1039 тыс., 865 тыс.,
694 тыс., 635 тыс. 1200. 11 см, 4 см, 15,625 см. 1201. b b c( ).+ 1202. 8 см.
1203. 12 см, 27 см. 1204. 21 см или 9 см. 1205. 72 см2
. 1206. 168 см2
или 224 см2
.
1207. 25 см или 5 97 см. 1208. 370 см2
. 1209. 1260 см2
. 1210. 546 см2
,
1621 см. 1211. 36 4 3 см. 1212. 150 см2
. 1213. p q
mr nr pn qn
n
+ + +
.
1214. 3 5 7. 1215. m2
mn n2
mn. 1216. 48 см. 1217. 13 см, 14 см, 15 см.
1218. 2 см. 1219. 12 м, 8 м, 6 м. 1220. 2 19 м. 1221. 7 см, 2 см;
3 см, 3 см. 1222. 8 см, 32 см, 20 см, 12 41 см. 1223. 2 см, 4 см. 1224. 14 см.
1225. 48 см2
. 1226. 18 см. 1227.
a( sin )
sin
1 4
8
2
+ α
α
. 1228. 2,88. 1229. 1044.
1230. 62°. 1231. r2
3 2 3+( ). 1232. b a b a( ).2 − 1233. 1
2
( ).P Q+ 1235. 2ab
a b+
.
1236.
1
1
−
+
k
k
. 1237.
a b
ab a b
+
− +
4
2 32 2
. 1238. a2
. 1239. 0,25 2S .
1240. S S1 2
2
+( ) . 1242. а) (q 1)(h 1); б) 3(2s 1)(3c 4z); в) (e s)
(3r 4d); г) (5z 3p)(6z 7q); д) (2m 3y)(5m 7g); е) 2(h f)(4j2
3f2
);
ж) (bm ny)(bm2
n2
y); з) (l s)(k2
k 1). 1243. а)
q l
q l
−
− − 1
; б)
e r
r
2 2
+
;
в)
t t
t
2
1
6 1
− +
+( )
; г)
e y
y
+
; д)
np
n p2 2
−
; е) lk
l k( )
;
+ 2
ж)
j
j
+
+
3
2
; з)
h
h
+
+
2
5
; и)
g
g
−
−
4
3
;
к)
f
f
+
+
1
7
; л)
z d s
z d s
− +
+ +
; м) c
a c+
. 1244. а)
1
1
−
+
b
b b( )
; б) 1
3
n n m( )
;
−
в)
a
a a
−
+
3
3( )
;
г)
q q
q
( )
;
5 4
5 4
−
+
д)
re r e
r e
( )
;
+
−
е) 1
3 2( )
;
y t−
ж)
d dp p
d p
2 2
2
− +
+( )
; з)
k l
l k kl l
+
− +2 2 2
( )
.
1245. а) 7
2 32
q q− −
; б)
h gj
j hg
+
+
; в) r
e r+
; г) 0; д) 1
( )( )
;
f d f s+ +
е) 0.
Правообладатель Народная асвета
Народная
асвета

95. 395
1246. а) b
c
; б) 1
xy
; в) 2a; г) a
a a
2
2
2 2− +
. 1247. а) 1; б) 3; в) 1; г) 3.
1248. а) (3; 7), − 5
3
14
3
; ; б) (0; 1), (2; 3), (1,5; 1); в) (2; 0), (2; 3), 5 2 5; ;+( )
− −( )5 2 5; ; г) ( 3; 2), ( 1; 4), (4; 5), (6; 3). 1249. а) (2,25; 1,75),
( 2,25; 1,75); б) (1,5; 0,5), − ±( )0 2 0 2 2, ; , ; в) (0,6; 0,75); г) 3 2 3; ,( )
− −( )3 2 3; ,
3 57
2
3 57
4
+ +
; ,
3 57
2
3 57
4
− −
; . 1251. а) ( 9; 5) ∪
∪ ( 5; 9); б) [ 10; 10]; в) ( ∞; 13] ∪ { 8} ∪ [13; ∞); г)[ 3; 1] ∪ [1; ∞);
д) ( ∞; 7) ∪ (5; 7); е) [ 11; 3] ∪ [11; ∞]; ж) ( 2; 1) ∪ (2; ∞); з) ( ∞; 4] ∪
∪ [ 3; 3]; и) ( ∞; 6) ∪ ( 5; ∞). 1252. а) (1,5; 5); б) − ; 11
7
∪ (4; ∞);
в) ( 3; 5); г) ( 3; 2) ∪ (2; 3); д) (1; 1,5) ∪ (2; ∞); е) ( ∞; 1) ∪ (0; 0,5) ∪
∪ (1; ∞); ж) ( 2; 1,5) ∪ (5; ∞); з) ( ∞; 3) ∪ ( 2; 1) ∪ (1; ∞);
и) ( ∞; 2) ∪ ( 1,25; 1) ∪ (1; 5); к) ( ∞; 5) ∪ ( 1; 1) ∪ (1,25; 2).
1253. а)
2 10
2
2 10
2
− +
; ; б) (0,5; 4); в) − −4 4
3
; ∪ (1; 2); г) 1,5.
1254. а) −14
9
; б) 2,5; −11
6
; в) 0,5; г) 6. 1255. а) 6 4 2; б) 11 3 13;
в) 14; г) 38 12 10. 1256. а) 11; б) 8; в) 6; г) 9. 1273. 42 км/ч, 54 км/ч.
1274. 8 дней, 12 дней. 1275. 1 мин. 1277. 2 дм. 1278. 48 дет. 1279. 3 км/ч.
1280. 5 А, 4 А. 1281. 315 км. 1282. 600 см3
, 1200 см3
.
Правообладатель Народная асвета
Народная
асвета

96. 396
Оглавление
Раздел I. Функции
1. Функция . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2. Функции y a
x
== , y = x3
, y x= . . . . . . . . . . . . . . . . . . . . . . . . 18
3. Свойства функций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Раздел II. Сочетание окружности с углом, прямой,
многоугольником
4. Окружность и угол . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
5. Угол и его меры . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
6. Окружность и прямая . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
7. Окружность и треугольник . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
8. Окружность и четырехугольник . . . . . . . . . . . . . . . . . . . . . . . 90
Раздел III. Неравенства
9. Квадратные неравенства. Рациональные неравенства . . . . . 103
10. Системы неравенств . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
Раздел IV. Соотношения между сторонами
и углами треугольника
11. Свойства треугольника . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
12. Площади треугольника и четырехугольника . . . . . . . . . . . 142
Раздел V. Системы уравнений
13. Рациональные уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . 159
14. Уравнение с двумя переменными . . . . . . . . . . . . . . . . . . . . . 171
15. Система уравнений с двумя переменными . . . . . . . . . . . . . 181
16. Нелинейные системы уравнений . . . . . . . . . . . . . . . . . . . . . 196
17. Решение задач с помощью систем уравнений . . . . . . . . . . . 204
Раздел VI. Последовательности
18. Числовая последовательность . . . . . . . . . . . . . . . . . . . . . . . . 211
19. Арифметическая прогрессия . . . . . . . . . . . . . . . . . . . . . . . . . 223
20. Геометрическая прогрессия . . . . . . . . . . . . . . . . . . . . . . . . . . 236
Раздел VII. Правильный многоугольник
и окружность
21. Правильные многоугольники . . . . . . . . . . . . . . . . . . . . . . . . 250
22. Длина окружности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 262
23. Площадь круга . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274
Правообладатель Народная асвета
Народная
асвета

97. 397
Раздел VIII. Основы школьной математики
24. Аксиоматический метод . . . . . . . . . . . . . . . . . . . . . . . . . . . . 283
25. Логические основы арифметики . . . . . . . . . . . . . . . . . . . . . . 297
26. Логические основы алгебры . . . . . . . . . . . . . . . . . . . . . . . . . 310
27. Логические основы геометрии . . . . . . . . . . . . . . . . . . . . . . . 323
Справочный материал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 340
Арифметика . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . —
Алгебра . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 354
Геометрия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 366
Таблицы значений тригонометрических функций . . . . . . . . . . 380
Ответы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 382
Правообладатель Народная асвета
Народная
асвета

98. 398
Учебное издание
Латотин Леонид Александрович
Чеботаревский Борис Дмитриевич
МАТЕМАТИКА
Учебное пособие для 9 класса
учреждений общего среднего образования
с русским языком обучения
4-е издание, исправленное и дополненное
Зав. редакцией В. Г. Бехтина. Редактор Е. И. Даниленко. Обложка художника
А. С. Хотеева. Технические рисунки А. Л. Латотина. Художественный
редактор Е. П. Протасеня. Техническое редактирование и компьютерная
верстка И. И. Дроздовой, И. И. Дубровской. Корректоры В. С. Бабеня, Е. П. Тхир,
А. В. Алешко.
Подписано в печать 24.04.2014. Формат 60 901
/16. Бумага офсетная.
Гарнитура школьная. Печать офсетная. Усл. печ. л. 25,0 + 0,25 форз.
Уч.-изд. л. 18,77 + 0,23 форз. Тираж 4000 экз. Заказ .
Издательское республиканское унитарное предприятие «Народная асвета»
Министерства информации Республики Беларусь.
Свидетельство о государственной регистрации издателя, изготовителя,
распространителя печатных изданий № 1/2 от 08.07.2013.
Пр. Победителей, 11, 220004, Минск.
ОАО «Полиграфкомбинат им. Я. Коласа».
Свидетельство о государственной регистрации издателя, изготовителя,
распространителя печатных изданий № 2/3 от 04.10.2013.
Ул. Корженевского, 20, 220024, Минск.
Правообладатель Народная асвета
Народная
асвета

99. 399
Латотин, Л. А.
Математика : учеб. пособие для 9-го кл. учреждений
общ. сред. образования с рус. яз. обучения / Л. А. Лато-
тин, Б. Д. Чеботаревский ; пер. с белорус. яз. Л. В. Лато-
тиной. — 4-е изд., испр. и доп. — Минск : Народная
асвета, 2014. — 397 с. : ил.
ISBN 978-985-03-2197-8.
Предыдущее издание вышло в 2008 г.
УДК 51(075.3=161.1)
ББК 22.1я721
Л27
Правообладатель Народная асвета
Народная
асвета

100. 400
_______________________________________________________________
(Название и номер учреждения образования)
Учебный
год
Имя и фамилия
учащегося
Состояние
учебного
пособия
при получении
Оценка
учащемуся
за пользование
учебным
пособием
20 /
20 /
20 /
20 /
20 /
Правообладатель Народная асвета
Народная
асвета