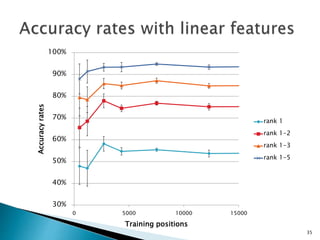
The document proposes using support vector machines (SVMs) with tree kernels to classify and rank moves in the game of mahjong based on a player's hand. Tree kernels allow SVMs to operate on tree structures representing mahjong hands without requiring feature engineering. An experiment applies this method to positions from expert mahjong games, achieving 57% accuracy in ranking expert moves first. The method shows promise for classifying positions that linear features cannot and could be improved by incorporating additional information from the game state.

1. Chikayama & Taura Lab.
M1 Ayato Miki
1

2. 1. Introduction
2. Related work
3. Proposed method
◦ SVM with kernels
◦ Tree kernels in mahjong
◦ Learning to rank using SVM
4. Experiment
5. Conclusion
2

3.  Features = elements to evaluate positions in
games
◦ e.g. Numbers and arrangements of pieces in Shogi
 Difficulty in creating features
◦ Require expert knowledge for the game
◦ Simple linear combinations are insufficient
 e.g. XOR
3

4.  Use kernels for evaluation features in games
◦ Simple inputs
 Tree structure
◦ Expect to work as non-linear features
 Implicit classification in high level feature space
4

5.  Classification of moves in mahjong using SVM
with kernels
◦ “Evaluation functions > search” in mahjong
 Kernel method is effective
◦ Tree kernels for tree structures of mahjong hands
 Similarity representation by kernel functions
◦ Use expert game records
 Learn “expert moves > other moves” with SVM
5

6. 1. Introduction
2. Related work
3. Proposed method
◦ SVM with kernels
◦ Tree kernels in mahjong
◦ Learning to rank using SVM
4. Experiment
5. Conclusion
6

7.  Machine learning using simple features
◦ TD-Gammon [Tesauro, 1992]
 Research about mahjong
◦ Learning from expert records [Kitagawa, 2007]
7

8. Game Mahjong
Features Manually picked
Method
Bonanza method
(without search)
Accuracy 56%
9

9. Features of player
面前の持ち牌
面前の持ち牌2枚の組み合わせ
面前の持ち牌3枚の組み合わせ
鳴いた牌の構成と状態
面子数
リャンメン数
カンチャン数とペンチャン数の和
トイツ数
テンパイしているかどうか
ドラの枚数
面前であるかどうか
親であるかどうか
リーチしているかどうか
自分が捨てたことのある牌
Features of
opponents
鳴いた牌の構成と状態
鳴いた回数
鳴いた牌の中で見えているドラの数
親であるかどうか
リーチしているかどうか
そのプレイヤに対する完全安牌
筋や壁などによって安全度が高い牌
自分との点差
Features of field
オーラスかどうか
見えていない牌の残り枚数
10

10. 1. Introduction
2. Related work
3. Proposed method
◦ SVM with kernels
◦ Tree kernels in mahjong
◦ Learning to rank using SVM
4. Experiment
5. Conclusion
11

11. 1. Introduction
2. Related work
3. Proposed method
◦ SVM with kernels
◦ Tree kernels in mahjong
◦ Learning to rank using SVM
4. Experiment
5. Conclusion
12

12.  2-class linear classifier
13
bxwxg 

)(
0)( xg

1)( xg

1)( xg

w

1
w

1
Maxmize margin
w

2

13.  Method for non-linear classification
)(xx


)()( 21 xx

  ),( 21 xxK

Explicit Replace
14

14. 1. Introduction
2. Related work
3. Proposed method
◦ SVM with kernels
◦ Tree kernels in mahjong
◦ Learning to rank using SVM
4. Experiment
5. Conclusion
15

15. 手牌
面子面子候補孤立牌
暗刻 暗順
リャンメン カンチャン トイツ
明刻
ペンチャン
…
Specific cards as leaves
16

16. 孤立牌 暗刻 暗順リャンメン カンチャン トイツペンチャン
17

17. 手牌
面子面子候補孤立牌
暗順リャンメン カンチャン
手牌
面子面子候補孤立牌
暗順リャンメン カンチャン
Count common subtrees
… … …
リャンメン
…
リャンメン
手牌
面子面子候補
暗順リャンメン
… …
面子候補
リャンメン
SST
18

18.  Deep subtrees are not very important
面子
暗順暗順 暗刻
depth
 )10(  
19

19.   

11 22
),(),( 2121
t tNn Nn
t nnttK


F
i
ii
fl
nInInn i
1
21
)(
21 )()(),( 
},,,{ 21 F
fffF 




0
1
)(nIi
tN
)( ifl
Set of nodes in tree t
Subtree set
Depth of subtree fi
otherwise
If fi is rooted at node n
20

20. 1. Introduction
2. Related work
3. Proposed method
◦ SVM with kernels
◦ Tree kernels in mahjong
◦ Learning to rank using SVM
4. Experiment
5. Conclusion
21

21.  SVM is just a 2-class classifier
◦ How learn to rank
 If you want to know ranks of three moves…
Order classifier ( > or < )
),(
),(
),(
32
31
21
mm
mm
mm
32
31
21
mm
mm
mm



213 mmm 
Rank
Input data -> Pairs of moves
22

22.  One training example has two tree instances
 Define kernel function for relative order
r
i
l
ii tte ,
),(),(),(),(),( 2121212121
lr
t
rl
t
rr
t
ll
ttr ttKttKttKttKeeK 
Classify “tl > tr” and “ tl< tr”
Label +1 when tl > tr
Label -1 when tl < tr
24

23. 1. Introduction
2. Related work
3. Proposed method
◦ SVM with kernels
◦ Tree kernels in mahjong
◦ Learning to rank using SVM
4. Experiment
5. Conclusion
25

24. 1. Experiment of proposed method
2. Error analysis
3. Comparison with related work
4. Practical player
26

25.  Machine spec
◦ Dual-Core AMD Opteron 2.4GHz
◦ 32GB RAM
 Implementation
◦ SVM-Light-TK [Moschitti, 2004]
 Soft margin trade-off parameter C=0.1
 Optimization threshold ε=0.1
27

26.  Learn from tsumo positions in expert records
◦ “Offensive” positions only
 Nobody declares “li-zhi”
 Nobody calls 3 or more “chi”, “pon” or “kan”
◦ Using records of Totugeki Tohoku
 ~285 games (~13,000 training positions)
 Evaluation
◦ Accuracy rates of trained classifiers
 Are expert moves ranked as the bests ?
◦ 4-fold cross validation
28

27. 30%
40%
50%
60%
70%
80%
90%
100%
0 2000 4000 6000 8000 10000 12000 14000
Accuracyrates
Training positions
rank 1
rank 1-2
rank 1-3
rank 1-5
29

28.  “Defensive” positions
31

29.  Positions require “yaku”(=poker hands) knowledge
32

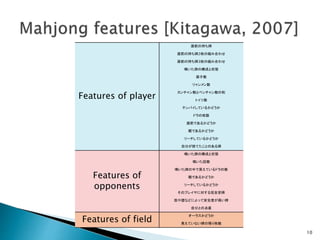
30.  Using features designed in [Kitagawa, 2007]
◦ Including board status information
 Implementation
◦ Ranking SVM in SVM-Light [Joachims, 2002]
34

31. 30%
40%
50%
60%
70%
80%
90%
100%
0 5000 10000 15000
Accuracyrates
Training positions
rank 1
rank 1-2
rank 1-3
rank 1-5
35

32.  Core2 Duo 1.06GHz
 91819 support vectors
 700ms for classification of one tree pair
 7 seconds for deciding one move
◦ 4 seconds in dual threading
◦ Good enough for playing against human players
36

33. 1. Introduction
2. Related work
3. Proposed method
◦ SVM with kernels
◦ Tree kernels in mahjong
◦ Learning to rank using SVM
4. Experiment
5. Conclusion
37

34.  Classified ranks of moves with tree kernels
◦ Possible with simple input
 57% accuracy
◦ Despite the lack of information of field and
opponents
◦ Increasing…
 Fine accuracy with permissible cost
38

35.  Classification analysis
◦ Positions that linear combinations cannot classify
 Refine tree structure
 Other information
◦ Hands information with other kernels
 String kernels
◦ Information of field and opponents
 Add as linear combinations or other kernels
 Heavy computing cost
◦ Classification time increases with a number of training
positions
◦ Indispensable in other games
39