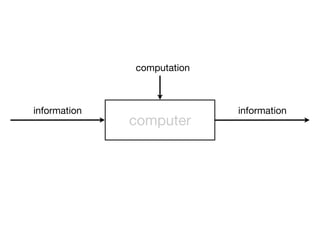
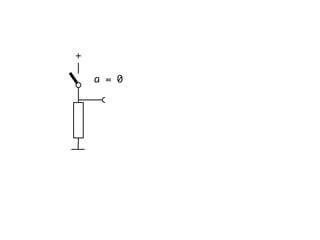
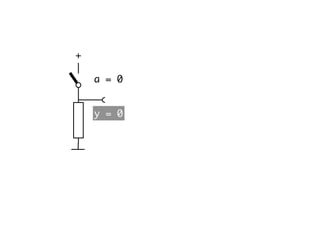
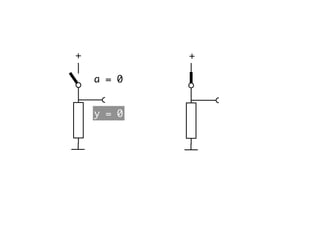
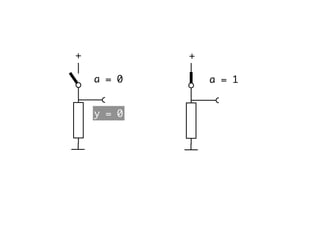
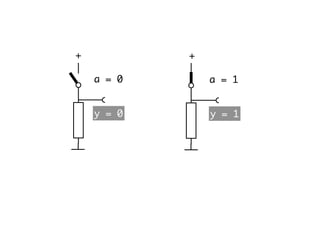
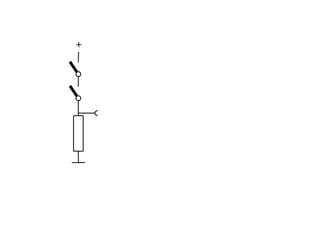
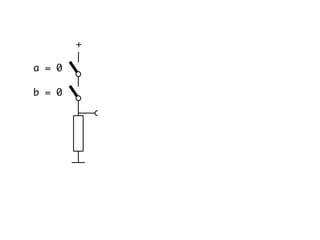
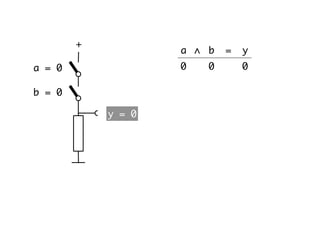
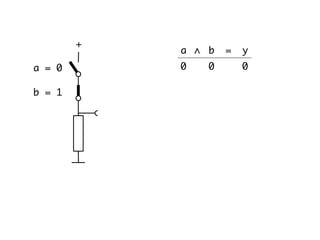
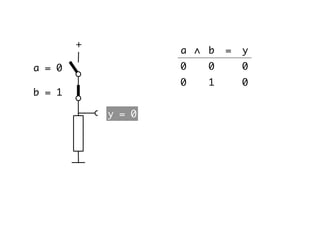
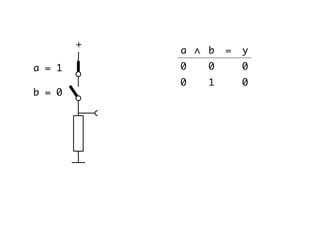
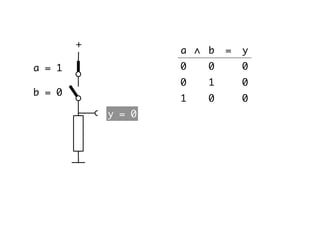
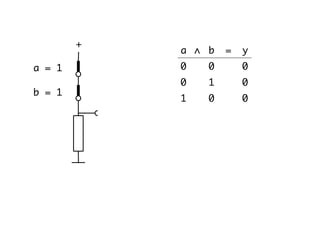
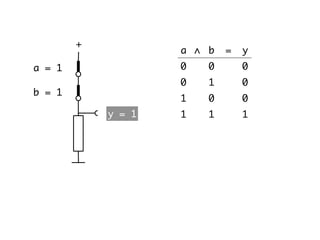
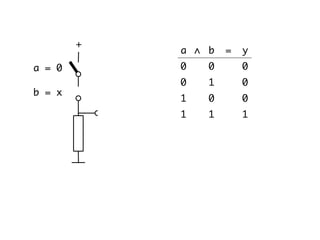
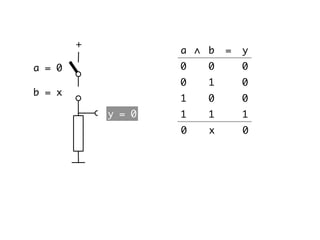
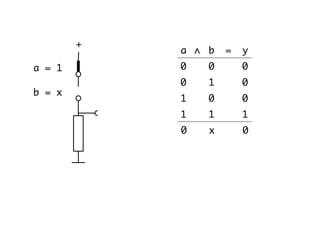
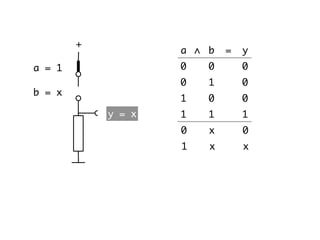
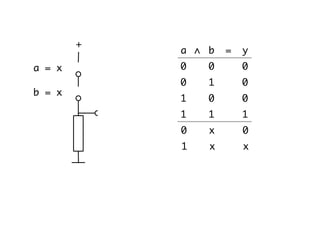
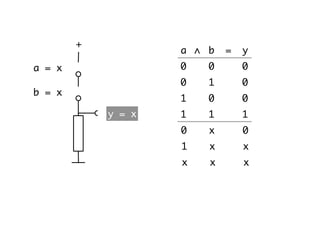
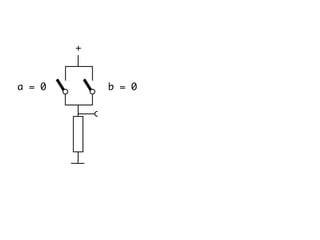
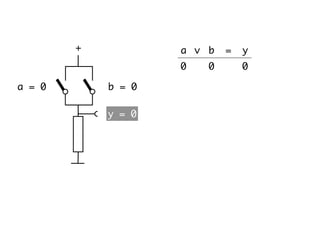
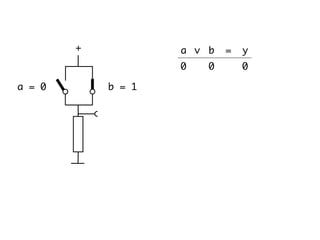
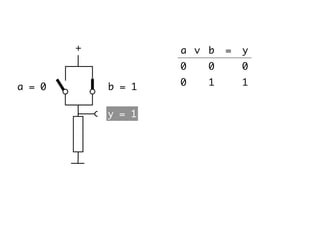
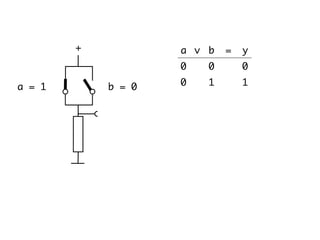
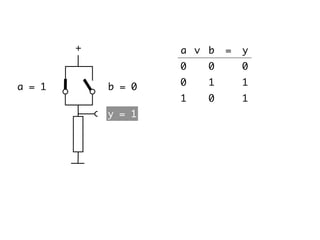
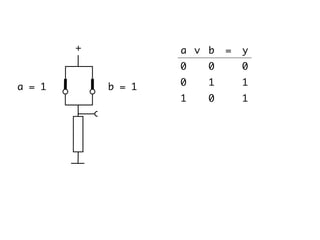
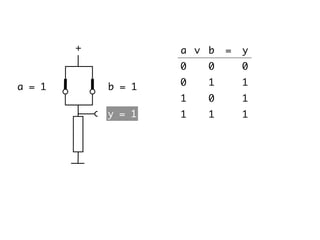
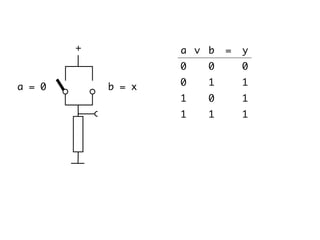
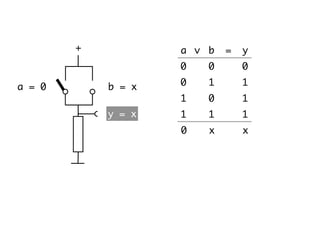
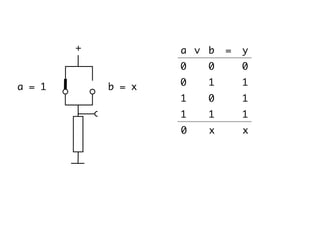
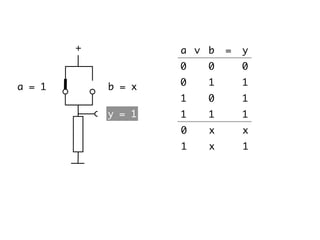
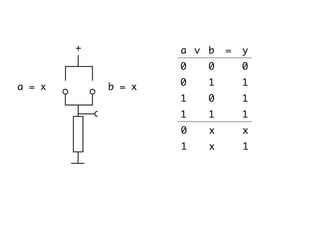
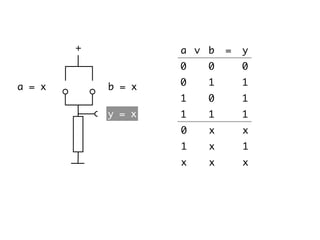
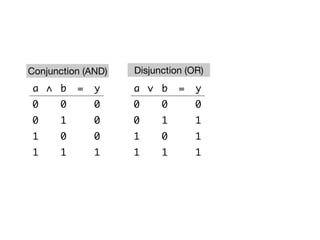
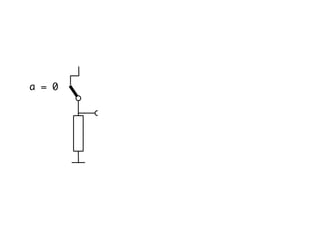
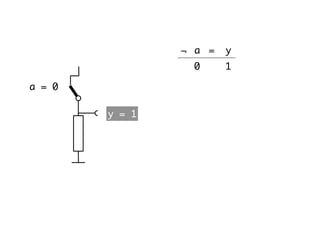
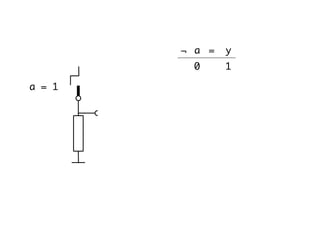
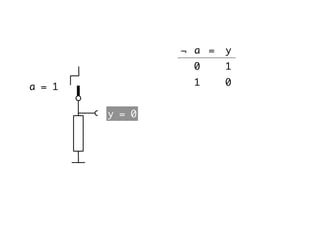
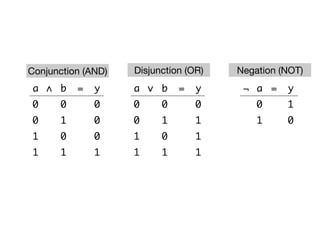
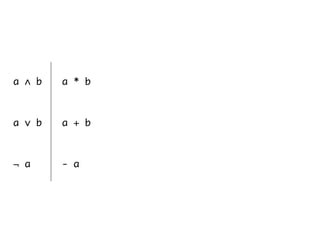
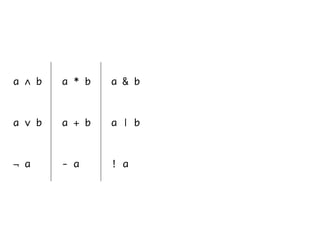
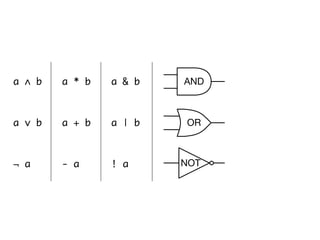
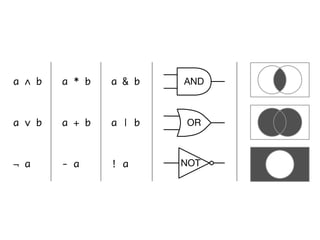
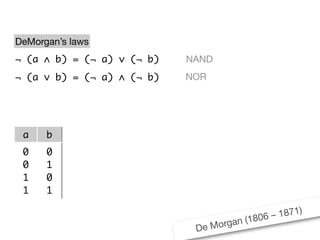
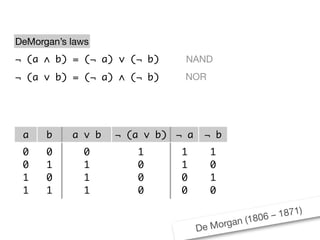
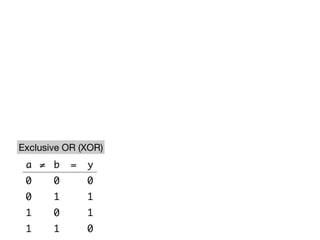
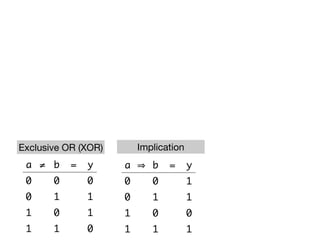
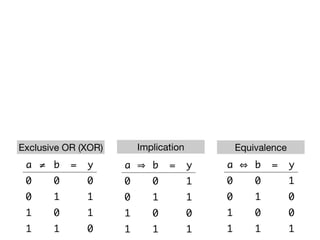
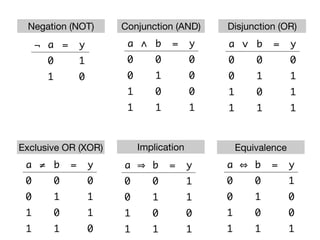
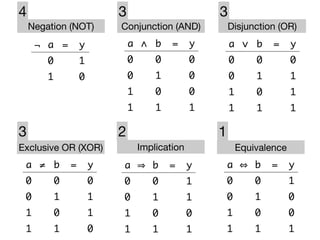
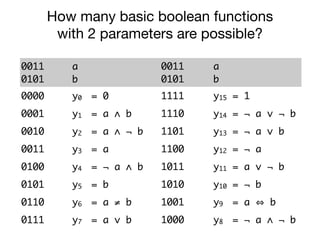
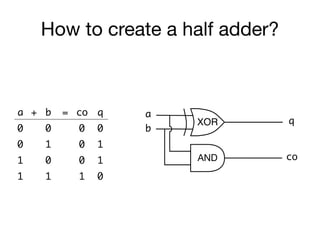
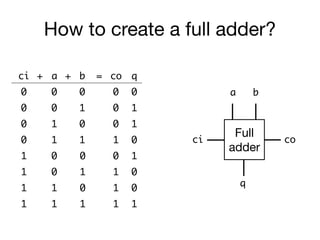
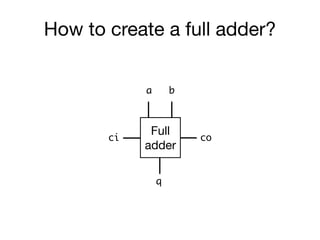
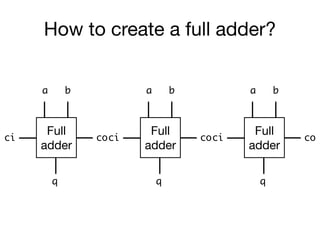
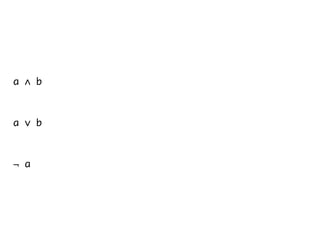The document presents an overview of Boolean algebra, detailing foundational concepts, operators, and laws, including conjunction, disjunction, negation, and various logical identities. Key figures in the development of Boolean algebra such as George Boole and Claude Shannon are mentioned, along with practical examples of Boolean functions and truth tables. It also covers important principles like De Morgan's laws and demonstrates how to derive various Boolean expressions.

1. Boolean
algebra
www.tudorgirba.com

2. computer
information information
computation

3. Alan Turing, 1937

4. George Boole
1815 – 1864

5. George Boole
1815 – 1864
Claude Shannon
1916 – 2001

7. +

8. +
a = 0

9. +
y = 0
a = 0

10. ++
y = 0
a = 0

11. +
a = 1
+
y = 0
a = 0

12. +
y = 1
a = 1
+
y = 0
a = 0

13. +

14. b = 0
a = 0
+

15. b = 0
a = 0
y = 0
∧ ba = y
00 0
+

16. b = 1
a = 0
∧ ba = y
00 0
+

17. b = 1
a = 0
y = 0
∧ ba = y
00 0
10 0
+

18. b = 0
a = 1
∧ ba = y
00 0
10 0
+

19. b = 0
a = 1
y = 0
∧ ba = y
00 0
10 0
01 0
+

20. b = 1
a = 1
∧ ba = y
00 0
10 0
01 0
+

21. b = 1
a = 1
y = 1
∧ ba = y
00 0
10 0
01 0
11 1
+

22. b = x
a = 0
∧ ba = y
00 0
10 0
01 0
11 1
+

23. b = x
a = 0
y = 0
∧ ba = y
00 0
10 0
01 0
11 1
x0 0
+

24. b = x
a = 1
∧ ba = y
00 0
10 0
01 0
11 1
x0 0
+

25. b = x
a = 1
y = x
∧ ba = y
00 0
10 0
01 0
11 1
x0 0
x1 x
+

26. b = x
a = x
∧ ba = y
00 0
10 0
01 0
11 1
x0 0
x1 x
+

27. b = x
a = x
y = x
∧ ba = y
00 0
10 0
01 0
11 1
x0 0
x1 x
xx x
+

28. a = 0 b = 0
+

29. a = 0 b = 0
y = 0
∨ ba = y
00 0
+

30. a = 0 b = 1
∨ ba = y
00 0
+

31. a = 0 b = 1
y = 1
∨ ba = y
00 0
10 1
+

32. a = 1 b = 0
∨ ba = y
00 0
10 1
+

33. a = 1 b = 0
y = 1
∨ ba = y
00 0
10 1
01 1
+

34. a = 1 b = 1
∨ ba = y
00 0
10 1
01 1
+

35. a = 1 b = 1
y = 1
∨ ba = y
00 0
10 1
01 1
11 1
+

36. a = 0 b = x
∨ ba = y
00 0
10 1
01 1
11 1
+

37. a = 0 b = x
y = x
∨ ba = y
00 0
10 1
01 1
11 1
x0 x
+

38. a = 1 b = x
∨ ba = y
00 0
10 1
01 1
11 1
x0 x
+

39. a = 1 b = x
y = 1
∨ ba = y
00 0
10 1
01 1
11 1
x0 x
x1 1
+

40. a = x b = x
∨ ba = y
00 0
10 1
01 1
11 1
x0 x
x1 1
+

41. a = x b = x
y = x
∨ ba = y
00 0
10 1
01 1
11 1
x0 x
x1 1
xx x
+

42. ∨ ba = y
00 0
10 1
01 1
11 1
∧ ba = y
00 0
10 0
01 0
11 1
Conjunction (AND) Disjunction (OR)

43. ∨ ba = y
00 0
10 1
01 1
11 1
∧ ba = y
00 0
10 0
01 0
11 1
?
Conjunction (AND) Disjunction (OR)

44. a = 0

45. a = 0
y = 1
a =¬ y
0 1

46. a = 1
a =¬ y
0 1

47. a = 1
y = 0
a =¬ y
0 1
1 0

48. ∨ ba = y
00 0
10 1
01 1
11 1
∧ ba = y
00 0
10 0
01 0
11 1
a =¬ y
0 1
1 0
Conjunction (AND) Disjunction (OR) Negation (NOT)

49. ¬ a
a ∧ b
a ∨ b

50. - a
a * b
a + b
¬ a
a ∧ b
a ∨ b

51. - a
a * b
a + b
¬ a
a ∧ b
a ∨ b
! a
a & b
a | b

52. - a
a * b
a + b
¬ a
a ∧ b
a ∨ b
! a
a & b
a | b
NOT
OR
AND

53. - a
a * b
a + b
¬ a
a ∧ b
a ∨ b
! a
a & b
a | b
NOT
OR
AND

55. a ∧ 1 = a
a ∨ 0 = a
Neutral elements

56. a ∧ 1 = a
a ∨ 0 = a
Neutral elements
a ∧ 0 = 0
a ∨ 1 = 1
Zero elements

57. a ∧ 1 = a
a ∨ 0 = a
Neutral elements
a ∧ 0 = 0
a ∨ 1 = 1
Zero elements
a ∧ a = a
a ∨ a = a
Idempotence

58. a ∧ 1 = a
a ∨ 0 = a
Neutral elements
a ∧ 0 = 0
a ∨ 1 = 1
Zero elements
a ∧ a = a
a ∨ a = a
Idempotence
a ∧ ¬ a = 0
a ∨ ¬ a = 1
Negation

59. a ∧ 1 = a
a ∨ 0 = a
Neutral elements
a ∧ 0 = 0
a ∨ 1 = 1
Zero elements
a ∧ a = a
a ∨ a = a
Idempotence
a ∧ ¬ a = 0
a ∨ ¬ a = 1
Negation
a ∨ b = b ∨ a
a ∧ b = b ∧ a
Commutativity

60. a ∧ 1 = a
a ∨ 0 = a
Neutral elements
a ∧ 0 = 0
a ∨ 1 = 1
Zero elements
a ∧ a = a
a ∨ a = a
Idempotence
a ∧ ¬ a = 0
a ∨ ¬ a = 1
Negation
a ∨ b = b ∨ a
a ∧ b = b ∧ a
Commutativity
a ∧ (b ∧ c) = (a ∧ b) ∧ c
a ∨ (b ∨ c) = (a ∨ b) ∨ c
Associativity

61. a ∧ 1 = a
a ∨ 0 = a
Neutral elements
a ∧ 0 = 0
a ∨ 1 = 1
Zero elements
a ∧ a = a
a ∨ a = a
Idempotence
a ∧ ¬ a = 0
a ∨ ¬ a = 1
Negation
a ∨ b = b ∨ a
a ∧ b = b ∧ a
Commutativity
a ∧ (b ∧ c) = (a ∧ b) ∧ c
a ∨ (b ∨ c) = (a ∨ b) ∨ c
Associativity
a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)
a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)
Distributivity

62. De Morgan (1806 – 1871)
¬ (a ∧ b) = (¬ a) ∨ (¬ b)
¬ (a ∨ b) = (¬ a) ∧ (¬ b)
DeMorgan’s laws
NAND
NOR

63. De Morgan (1806 – 1871)
¬ (a ∧ b) = (¬ a) ∨ (¬ b)
¬ (a ∨ b) = (¬ a) ∧ (¬ b)
a b a ∨ b ¬ (a ∨ b) ¬ a ¬ b (¬ a) ∧ (¬ b)
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
DeMorgan’s laws
NAND
NOR

64. De Morgan (1806 – 1871)
¬ (a ∧ b) = (¬ a) ∨ (¬ b)
¬ (a ∨ b) = (¬ a) ∧ (¬ b)
a b a ∨ b ¬ (a ∨ b) ¬ a ¬ b (¬ a) ∧ (¬ b)
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
DeMorgan’s laws
NAND
NOR

65. De Morgan (1806 – 1871)
¬ (a ∧ b) = (¬ a) ∨ (¬ b)
¬ (a ∨ b) = (¬ a) ∧ (¬ b)
a b a ∨ b ¬ (a ∨ b) ¬ a ¬ b (¬ a) ∧ (¬ b)
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
DeMorgan’s laws
NAND
NOR

66. De Morgan (1806 – 1871)
¬ (a ∧ b) = (¬ a) ∨ (¬ b)
¬ (a ∨ b) = (¬ a) ∧ (¬ b)
a b a ∨ b ¬ (a ∨ b) ¬ a ¬ b (¬ a) ∧ (¬ b)
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
DeMorgan’s laws
NAND
NOR

67. De Morgan (1806 – 1871)
¬ (a ∧ b) = (¬ a) ∨ (¬ b)
¬ (a ∨ b) = (¬ a) ∧ (¬ b)
a b a ∨ b ¬ (a ∨ b) ¬ a ¬ b (¬ a) ∧ (¬ b)
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
DeMorgan’s laws
NAND
NOR

68. De Morgan (1806 – 1871)
¬ (a ∧ b) = (¬ a) ∨ (¬ b)
¬ (a ∨ b) = (¬ a) ∧ (¬ b)
a b a ∨ b ¬ (a ∨ b) ¬ a ¬ b (¬ a) ∧ (¬ b)
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
DeMorgan’s laws
NAND
NOR

69. De Morgan (1806 – 1871)
¬ (a ∧ b) = (¬ a) ∨ (¬ b)
¬ (a ∨ b) = (¬ a) ∧ (¬ b)
a b a ∨ b ¬ (a ∨ b) ¬ a ¬ b (¬ a) ∧ (¬ b)
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
DeMorgan’s laws
NAND
NOR

70. a ∧ 1 = a a ∨ b = b ∨ a
a ∨ 0 = a
a ∧ 0 = 0
a ∨ 1 = 1
a ∧ a = a
a ∨ a = a
a ∧ ¬ a = 0
a ∨ ¬ a = 1
Neutral elements
Zero elements
Idempotence
Negation
a ∧ (b ∧ c) = (a ∧ b) ∧ c
a ∧ b = b ∧ a
a ∨ (b ∨ c) = (a ∨ b) ∨ c
a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)
a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)
¬ (a ∧ b) = (¬ a) ∨ (¬ b)
¬ (a ∨ b) = (¬ a) ∧ (¬ b)
Commutativity
Associativity
Distributivity
DeMorgan’s

72. ≠ ba = y
00 0
10 1
01 1
11 0
Exclusive OR (XOR)

73. ≠ ba = y
00 0
10 1
01 1
11 0
Exclusive OR (XOR)
ba = y
00 1
10 1
01 0
11 1
Implication

74. ≠ ba = y
00 0
10 1
01 1
11 0
Exclusive OR (XOR)
ba = y
00 1
10 1
01 0
11 1
ba = y
00 1
10 0
01 0
11 1
Implication Equivalence

75. ≠ ba = y
00 0
10 1
01 1
11 0
Exclusive OR (XOR)
ba = y
00 1
10 1
01 0
11 1
ba = y
00 1
10 0
01 0
11 1
Implication Equivalence
∨ ba = y
00 0
10 1
01 1
11 1
∧ ba = y
00 0
10 0
01 0
11 1
Conjunction (AND) Disjunction (OR)
a =¬ y
0 1
1 0
Negation (NOT)

76. ≠ ba = y
00 0
10 1
01 1
11 0
Exclusive OR (XOR)
ba = y
00 1
10 1
01 0
11 1
ba = y
00 1
10 0
01 0
11 1
Implication Equivalence
∨ ba = y
00 0
10 1
01 1
11 1
∧ ba = y
00 0
10 0
01 0
11 1
Conjunction (AND) Disjunction (OR)
a =¬ y
0 1
1 0
Negation (NOT)
4 3 3
3 2 1

77. Tautology
f = 1 (a ∧ (a b)) b
Contradiction
f = 0 a ∧ (¬ a)
Satisfiable
f = 1 sometimes a b

78. How many basic boolean functions
with 2 parameters are possible?

79. How many basic boolean functions
with 2 parameters are possible?

80. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

81. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

82. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

83. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

84. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

85. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

86. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

87. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

88. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

89. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

90. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

91. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

92. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

93. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

94. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

95. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

96. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

97. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?

98. 0011
0101
a
b
0000 y0 = 0
0001 y1 = a ∧ b
0010 y2 = a ∧ ¬ b
0011 y3 = a
0100 y4 = ¬ a ∧ b
0101 y5 = b
0110 y6 = a ≠ b
0111 y7 = a ∨ b
How many basic boolean functions
with 2 parameters are possible?
0011
0101
a
b
1111 y15 = 1
1110 y14 = ¬ a ∨ ¬ b
1101 y13 = ¬ a ∨ b
1100 y12 = ¬ a
1011 y11 = a ∨ ¬ b
1010 y10 = ¬ b
1001 y9 = a b
1000 y8 = ¬ a ∧ ¬ b

99. How to create a half adder?

100. How to create a half adder?
+ ba = co
00 0
10 0
01 0
11 1
q
0
1
1
0

101. How to create a half adder?
a
b
q
co
+ ba = co
00 0
10 0
01 0
11 1
q
0
1
1
0
AND
XOR

102. How to create a full adder?

103. How to create a full adder?
+ ba = co
00 0
10 0
01 0
11 1
q
0
1
1
0
ci +
0
0
0
0
1
1
1
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1

104. How to create a full adder?
+ ba = co
00 0
10 0
01 0
11 1
q
0
1
1
0
ci +
0
0
0
0
1
1
1
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
Full
adder
a b
coci
q

105. How to create a full adder?
Full
adder
a b
coci
q

106. How to create a full adder?
Full
adder
a b
coci
q
Full
adder
a b
coci
q
Full
adder
a b
coci
q

107. Tudor Gîrba
www.tudorgirba.com
creativecommons.org/licenses/by/3.0/