1. ชื่อวิชา ดิจิตอลเบื้องต้น ( Introduction to Digital ) รหัสวิชา 4121701

2. บทที่ 1 ระบบเลขฐาน ความสัมพันธ์ระหว่างเลขฐานสิบและเลขฐานสอง ระบบเลขฐานสอง ระบบเลขฐานแปด 1 ระบบเลขฐานสิบ 2 3 4

3. บทที่ 1 ระบบเลขฐาน ระบบเลขฐานสิบหก การเปลี่ยนเลขฐานสองเป็นเลขฐานแปดและเลขฐานสิบหก การเปลี่ยนเลขฐานระหว่างฐานสองกับฐานสิบหก การเปลี่ยนเลขฐานระหว่างฐานแปดกับฐานสิบหก 5 การเปลี่ยนเลขฐานสิบเป็นเลขฐานอื่น 6 7 8 9

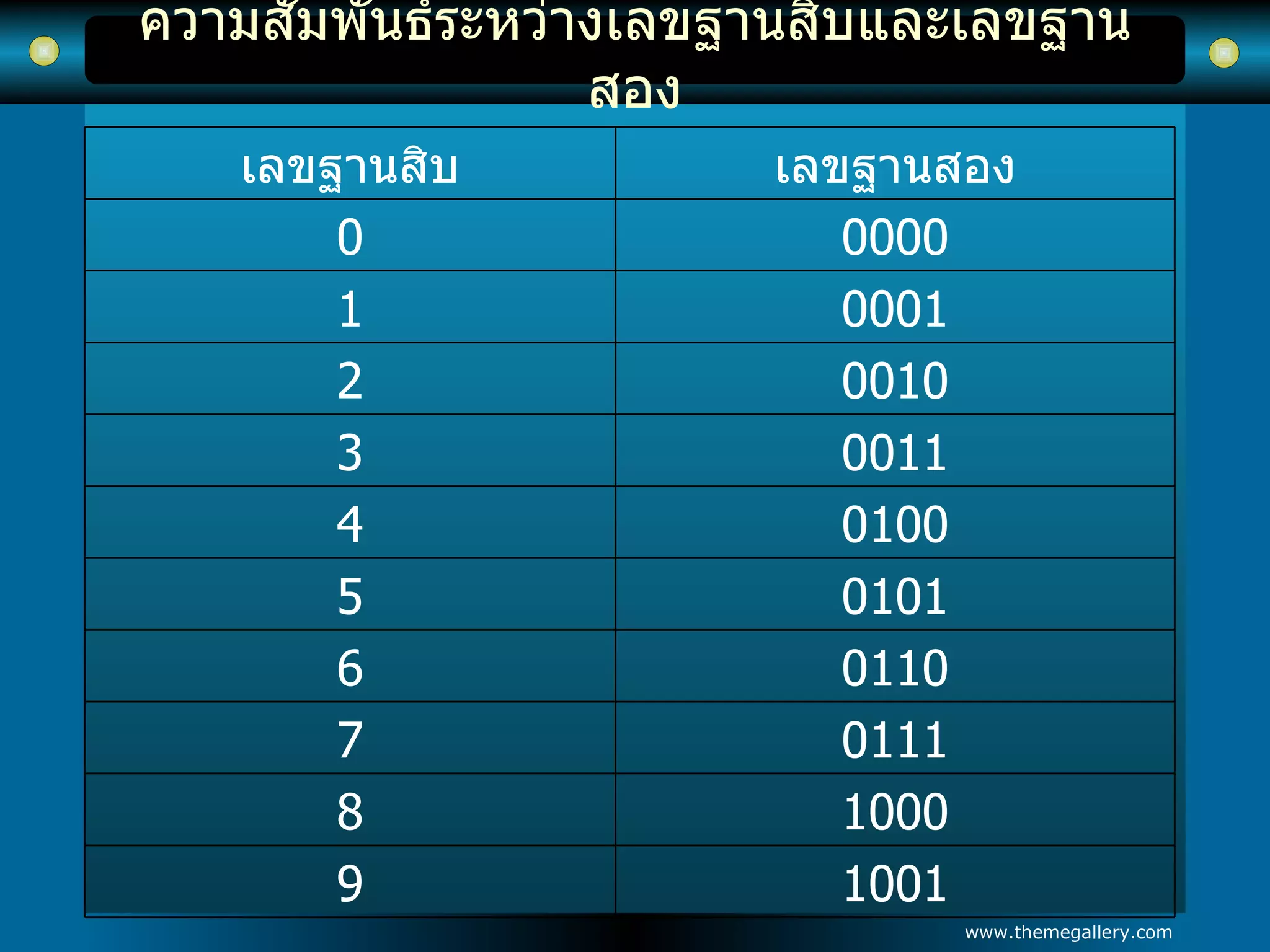
4. ระบบเลขฐาน 1. ความสัมพันธ์ระหว่างเลขฐานสิบและเลขฐานสอง จำนวนเลขฐานสิบประกอบด้วย เลข 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ซึ่งประกอบ ด้วยเลขจำนวนทั้งหมด 10 ตัว จึงเรียกว่าเลขฐานสิบ จำนวนเลขฐานสองประกอบด้วย เลข 0 และ 1 จึงเรียกว่าเลขฐานสอง

5. ความสัมพันธ์ระหว่างเลขฐานสิบและเลขฐานสอง 1001 9 1000 8 0111 7 0110 6 0101 5 0100 4 0011 3 0010 2 0001 1 0000 0 เลขฐานสอง เลขฐานสิบ

6. 2. ระบบเลขฐานสิบ ระบบเลขฐานสิบมีตำแหน่งและค่าน้ำหนักที่มีลำดับความสำคัญต่างกัน การเรียงลำดับเรียงจากค่าน้อยไปหาค่ามาก เริ่มจากค่าความสำคัญน้อยที่สุด ( LSD = Least Significant Digit) อยู่ทางด้านขวามือ และเพิ่มขึ้นเรื่อยๆ จนถึงค่าความสำคัญมากสุด (MSD = Most Significant Digit ) ทางด้านซ้ายมือ

7. 2. ระบบเลขฐานสิบ การเขียนค่าตัวเลขในแต่ละหลักสามารถเขียนได้สองรูปแบบ คือเขียนเป็นค่าปกติ และเขียนในรูปของเลขยกกำลัง 10 -3 10 -2 10 -1 10 0 10 1 10 2 10 3 10 4 0.001 0.01 0.1 1 10 100 1,000 10,000 ทศนิยมที่ 3 ทศนิยมที่ 2 ทศนิยมที่ 1 หลักหน่วย หลักสิบ หลักร้อย หลักพัน หลักหมื่น

8. ตัวอย่างที่ 1

9. ตัวอย่างที่ 2

10. ตัวอย่างที่ 3

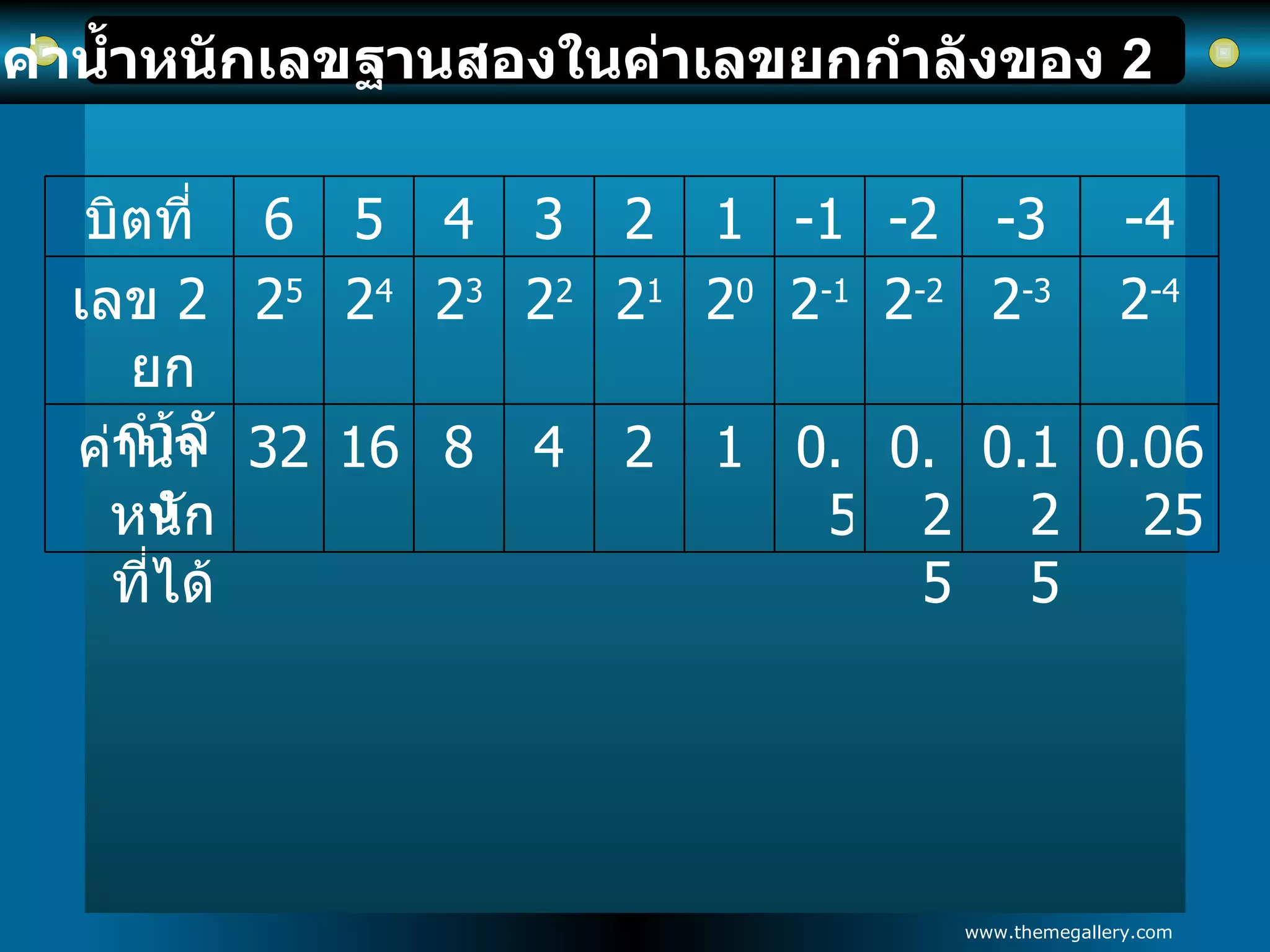
11. 3. ระบบเลขฐานสอง เลขฐานสองมีเพียงสองค่าเท่านั้นคือ เลข 0 และ เลข 1 เหมาะกับการใช้งานกับดิจิตอลและคอมพิวเตอร์ ตัวเลขแต่ละหลักจะถูกเรียกว่า บิต มาจากคำเต็ม Binary Digit เช่น มีเลขฐานสอง 5 ตัวเรียกว่า 5 บิต การแสดงตำแหน่งของระบบเลขฐานสองใช้หลักแสดงตำแหน่ง เรียงลำดับจากความสำคัญน้อย เรียกว่าบิตสำคัญน้อยสุด (LSB = Least Significant Bit ) อยู่ด้านขวามือ เรียงลำดับความสำคัญมากขึ้นไปถึงสำคัญมากสุด เรียกว่า บิตสำคัญมากสุด (MSB = Most Significant Bit ) อยู่ด้านซ้ายมือ

12. ค่าน้ำหนักเลขฐานสองในค่าเลขยกกำลังของ 2 0.0625 0.125 0.25 0.5 1 2 4 8 16 32 ค่าน้ำหนักที่ได้ 2 -4 2 -3 2 -2 2 -1 2 0 2 1 2 2 2 3 2 4 2 5 เลข 2 ยกกำลัง -4 -3 -2 -1 1 2 3 4 5 6 บิตที่

13. ตัวอย่างที่ 4

14. ตัวอย่างที่ 5

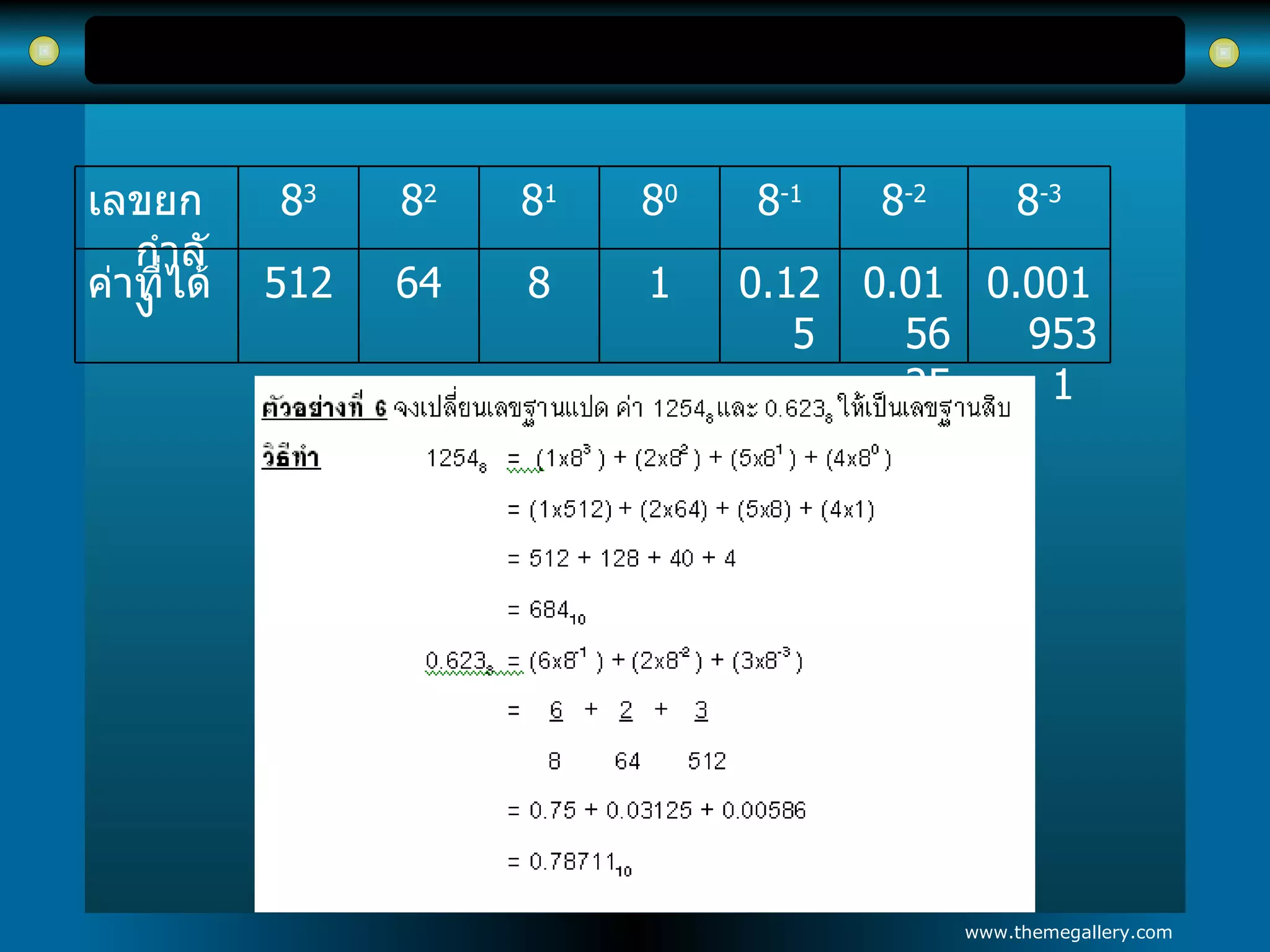
15. 4. ระบบเลขฐานแปด ระบบเลขฐานแปดถูกนำมาใช้กับคอมพิวเตอร์ในยุคแรกๆ เพราะเป็นการลดจำนวนจากเลขฐานสิบให้น้อยลง ซึ่งเลขฐานแปดประกอบด้วย 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 เป็นจำนวนทั้งหมด 8 ตัวจึงเรียกว่าเลขฐานแปด

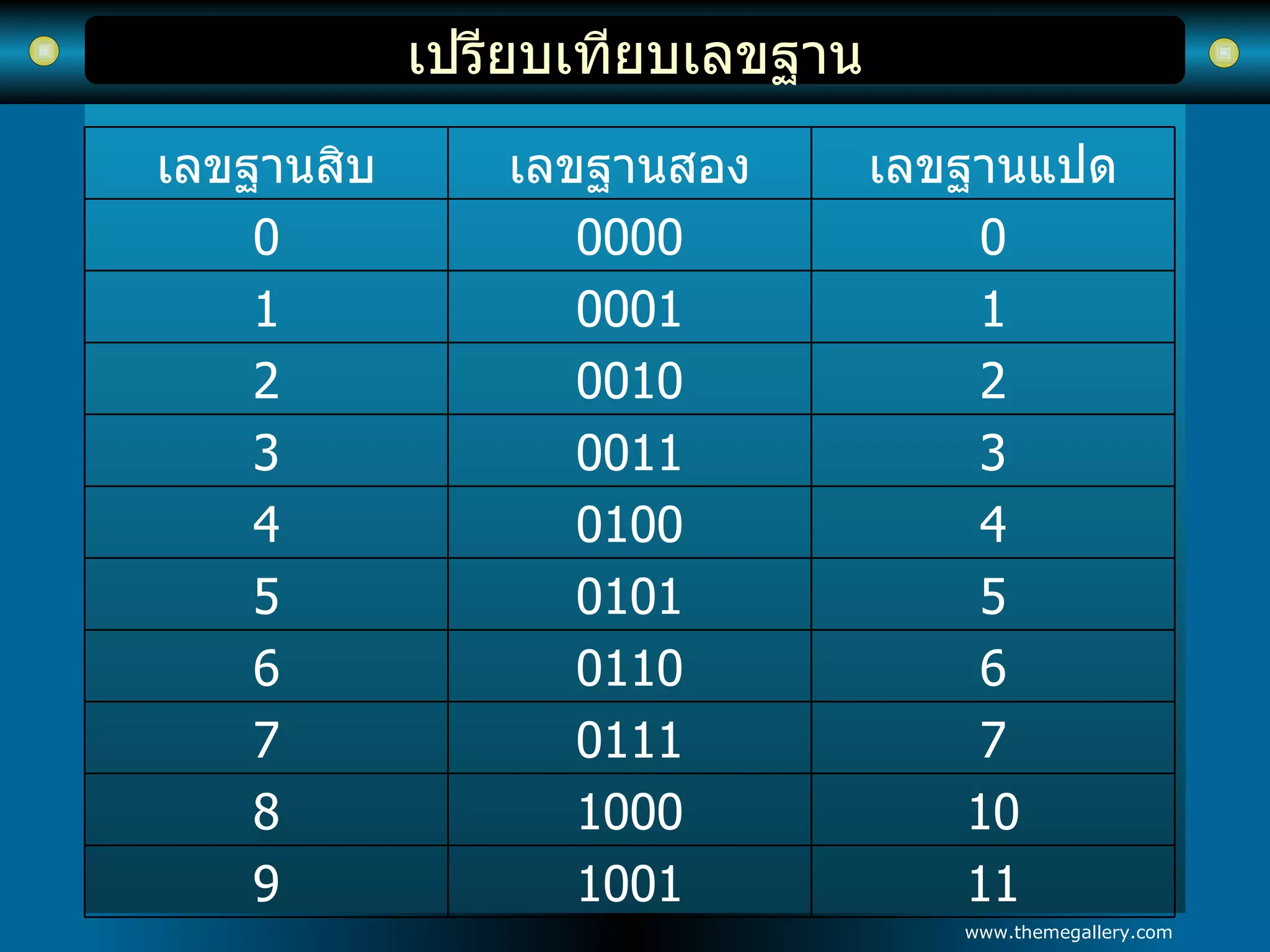
16. เปรียบเทียบเลขฐาน 11 1001 9 10 1000 8 7 0111 7 6 0110 6 5 0101 5 4 0100 4 3 0011 3 2 0010 2 1 0001 1 0 0000 0 เลขฐานแปด เลขฐานสอง เลขฐานสิบ

17. 0.0019531 0.015625 0.125 1 8 64 512 ค่าที่ได้ 8 -3 8 -2 8 -1 8 0 8 1 8 2 8 3 เลขยกกำลัง

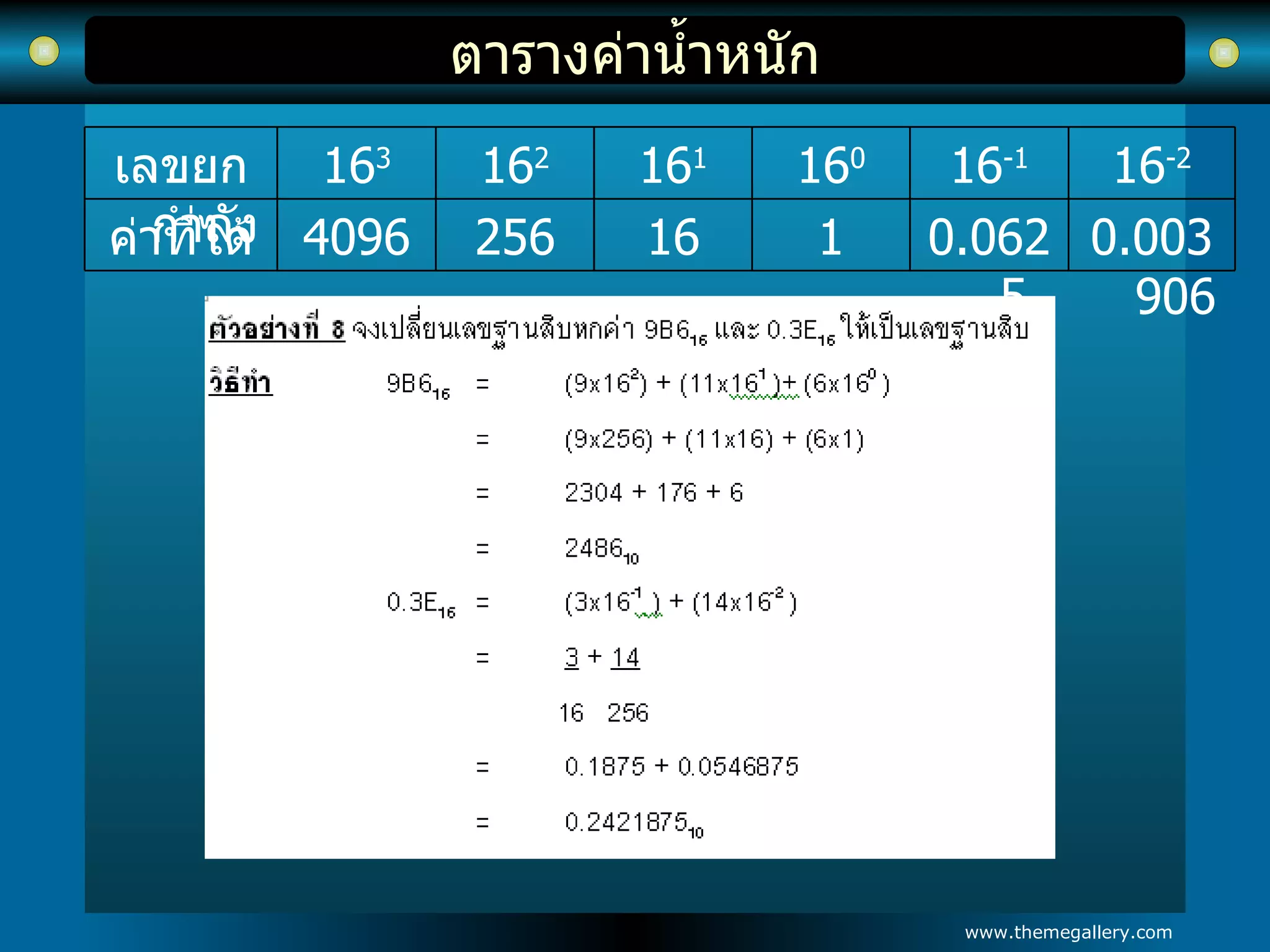
18. 5. ระบบเลขฐานสิบหก เลขฐานสิบหกประกอบด้วย 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , A , B , C , D , E , F จำนวนทั้งหมด 16 ตัวเรียกว่าเลขฐานสิบหก

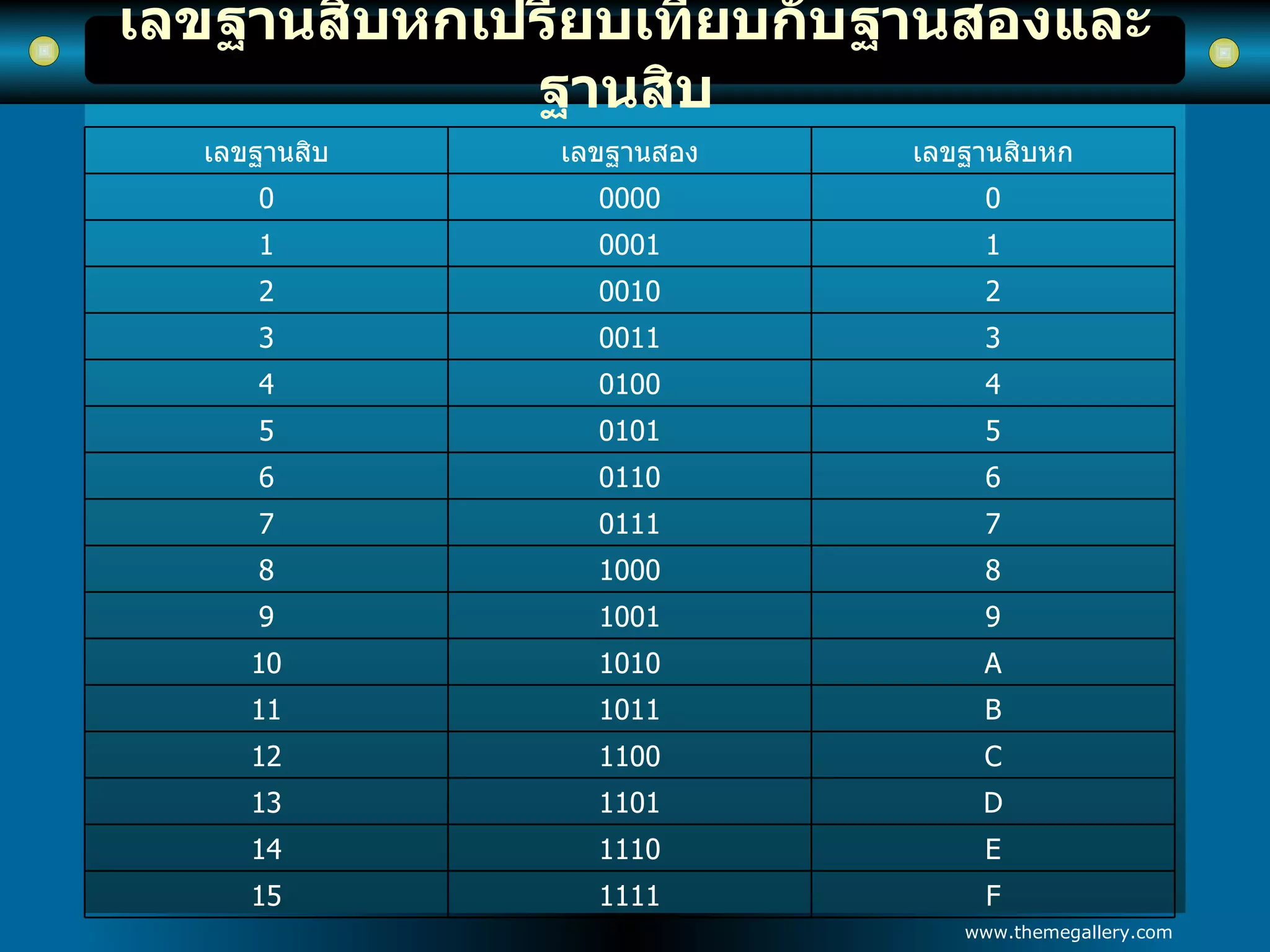
19. เลขฐานสิบหกเปรียบเทียบกับฐานสองและฐานสิบ F 1111 15 E 1110 14 D 1101 13 C 1100 12 B 1011 11 A 1010 10 9 1001 9 8 1000 8 7 0111 7 6 0110 6 5 0101 5 4 0100 4 3 0011 3 2 0010 2 1 0001 1 0 0000 0 เลขฐานสิบหก เลขฐานสอง เลขฐานสิบ

20. ตารางค่าน้ำหนัก 0.003906 0.0625 1 16 256 4096 ค่าที่ได้ 16 -2 16 -1 16 0 16 1 16 2 16 3 เลขยกกำลัง

21. 6. การเปลี่ยนเลขฐานสิบเป็นเลขฐานอื่น

24. 7. การเปลี่ยนเลขฐานสองเป็นเลขฐานแปดและเลขฐานสิบหก การเปลี่ยนเลขฐานสองเป็นฐานแปดให้ใช้วิธีการแบ่งเลขฐานสองออกเป็น 3 บิต โดยบิตทางขวาสุดมีค่าเท่ากับ 1 และเพิ่มขึ้นแบบทวีคูณมาทางด้านซ้าย คือ 4 2 1

25. 8. การเปลี่ยนเลขฐานระหว่างฐานสองกับฐานสิบหก การเปลี่ยนเลขฐานสองเป็นฐานสิบหกให้ใช้วิธีการแบ่งเลขฐานสองออกเป็น 4 บิต โดยบิตทางขวาสุดมีค่าเท่ากับ 1 และเพิ่มขึ้นแบบทวีคูณมาทางด้านซ้าย คือ 8 4 2 1

26. 9. การเปลี่ยนเลขฐานระหว่างฐานแปดกับฐานสิบหก การเปลี่ยนเลขฐานแปดเป็นฐานสิบหกหรือฐานสิบหกเป็นฐานแปดให้ทำการเปลี่ยนเป็นเลขฐานสองก่อน แล้วจึงปรับบิตของฐานแปดเป็น 3 บิต และปรับบิตฐานสิบหกเป็น 4 บิต

28. แบบทดสอบ เลขฐานต่างๆ 1. จงเปลี่ยนเลขฐานต่างๆ ให้เป็นเลขฐานสิบ 1.1 1001101.100111 2 1.2 2750.36 8 1.3 58E.4D 16 2. จงเปลี่ยนเลขฐานสิบให้เป็นเลขฐานต่างๆ 2.1 369.502 10 ให้เป็นฐานสอง 2.2 541.36 10 ให้เป็นฐานแปด 2.3 8264.78 10 ให้เป็นฐานสิบหก 3. จงเปลี่ยนเลขฐานแปดกับฐานสิบหก 3.1 4561.526 8 ให้เป็นฐานสิบหก 3.2 A92C.5E4 16 ให้เป็นฐานแปด