あるLTで使う為の資料

1. ある最適停止問題の解
2016.01.30 下野寿之
1

2. 例題-1
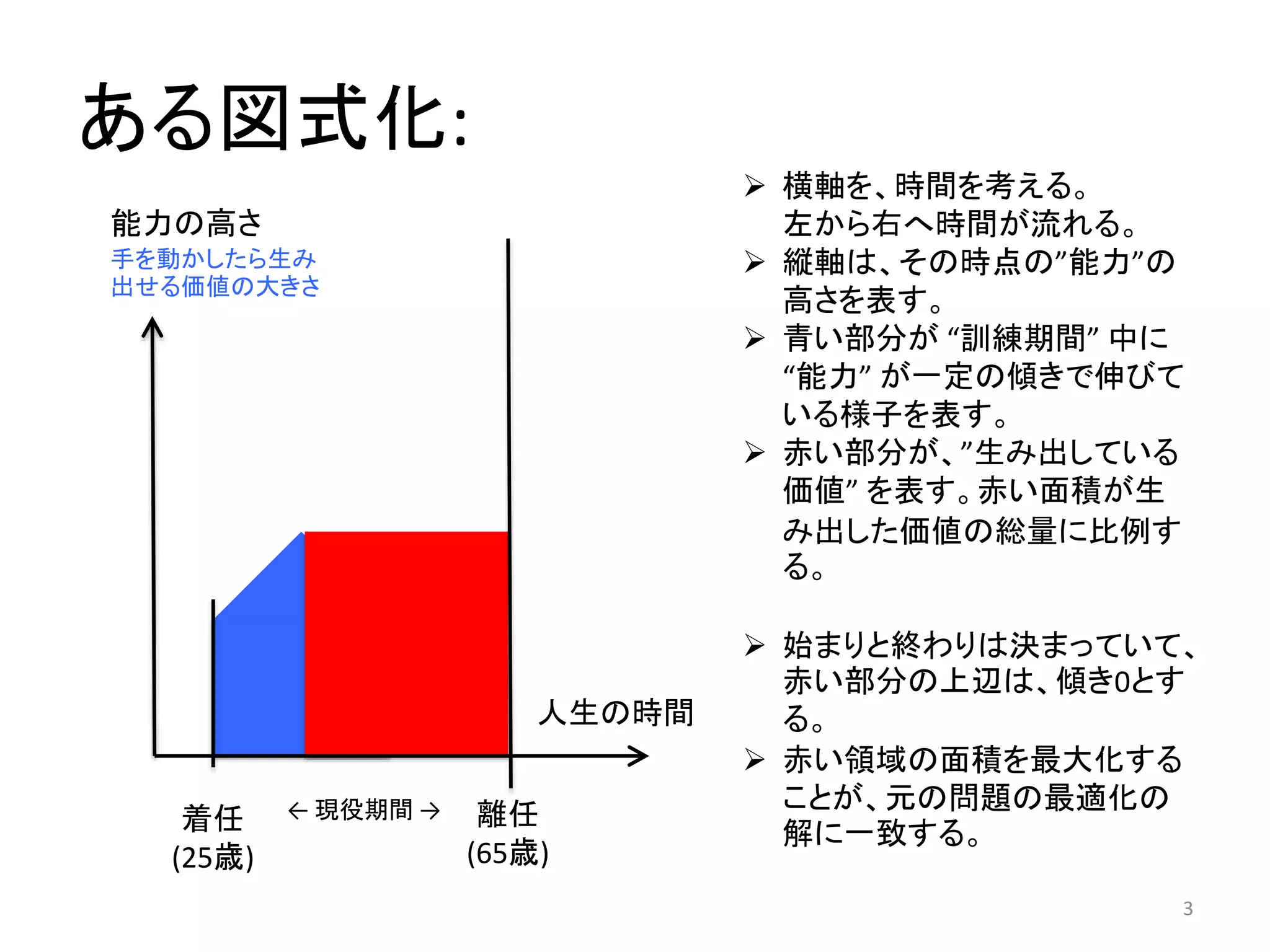
 問題設定 :
- ある病院にある心臓外科医が雇われているとする。
- ”訓練” の経験時間に比例して、”能力が増大” し、
単位時間当たり(例, 1週間または1ヶ月)に行える “手術” によって、
救える人の命の数が増える( “価値を出力” する) ものとする。
- ただし、”訓練” ではない時間(手術をしている時間を含む) は
その能力が増えないものとする。
- その医師が(25歳で)着任してから(65歳で)定年になるまでの
現役期間にどういう訓練期間を与えると、
救える人の命の数が、最大になるだろうか?
2
ここに記載した問題設定は、後で述べる理屈を分かり安く説明するための例として、
心臓外科医を持ち出したのであって、医療の問題をこのスライドで触れる訳では全
くありません。伝統工芸品を作る人が、生涯の製造品の価値の総和を最大化する
問題として置き換えることができます。具体例はいくらでも作れます。

3. ある図式化:
3
人生の時間
着任
(25歳)
離任
(65歳)
← 現役期間 →
能力の高さ
手を動かしたら生み
出せる価値の大きさ
 横軸を、時間を考える。
左から右へ時間が流れる。
 縦軸は、その時点の”能力”の
高さを表す。
 青い部分が “訓練期間” 中に
“能力” が一定の傾きで伸びて
いる様子を表す。
 赤い部分が、”生み出している
価値” を表す。赤い面積が生
み出した価値の総量に比例す
る。
 始まりと終わりは決まっていて、
赤い部分の上辺は、傾き0とす
る。
 赤い領域の面積を最大化する
ことが、元の問題の最適化の
解に一致する。

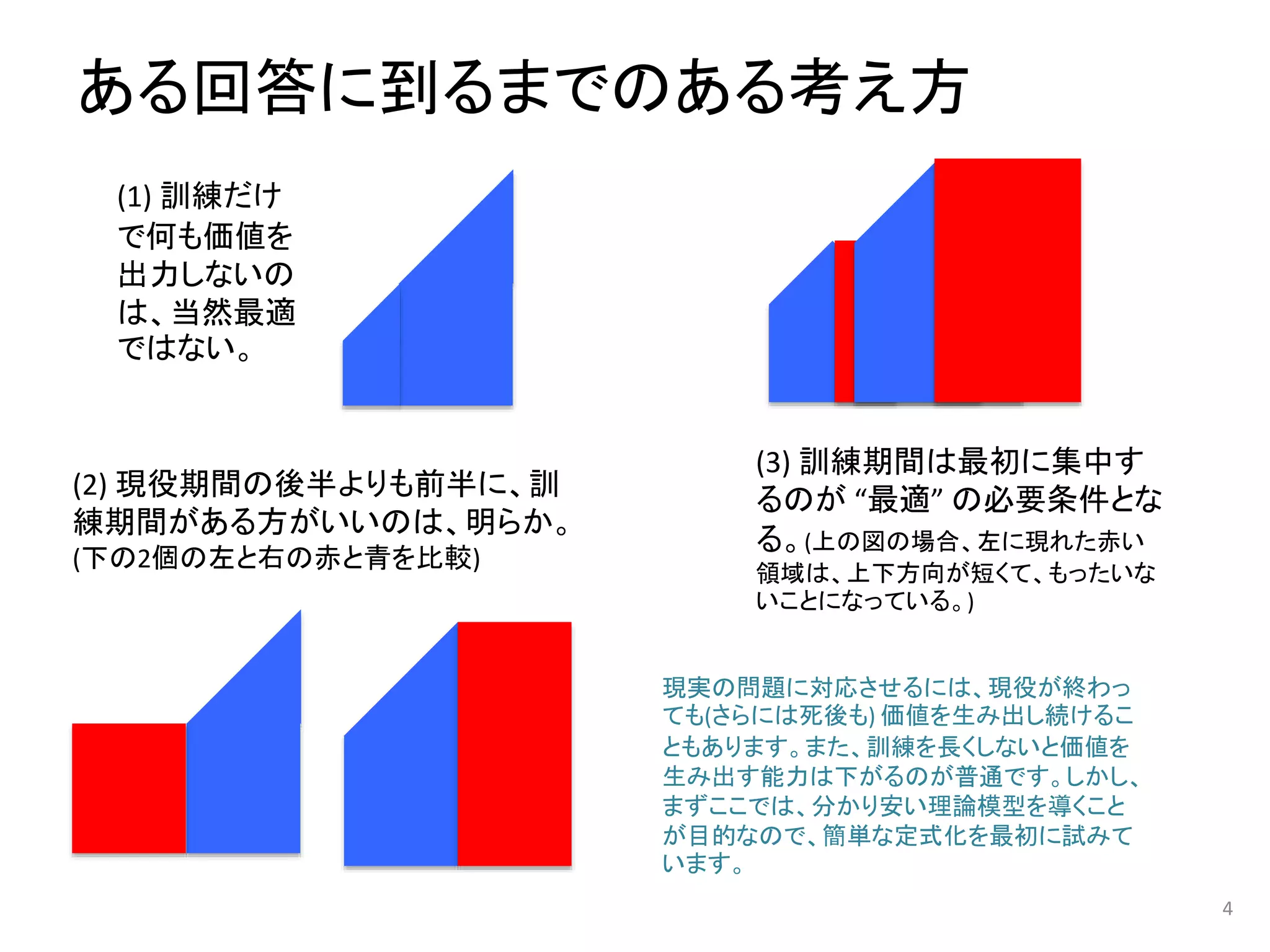
4. ある回答に到るまでのある考え方
4
(3) 訓練期間は最初に集中す
るのが “最適” の必要条件とな
る。(上の図の場合、左に現れた赤い
領域は、上下方向が短くて、もったいな
いことになっている。)
(1) 訓練だけ
で何も価値を
出力しないの
は、当然最適
ではない。
(2) 現役期間の後半よりも前半に、訓
練期間がある方がいいのは、明らか。
(下の2個の左と右の赤と青を比較)
現実の問題に対応させるには、現役が終わっ
ても(さらには死後も) 価値を生み出し続けるこ
ともあります。また、訓練を長くしないと価値を
生み出す能力は下がるのが普通です。しかし、
まずここでは、分かり安い理論模型を導くこと
が目的なので、簡単な定式化を最初に試みて
います。

5. 例題-1 の解
5
人生の時間
着任
(25歳)
離任
(65歳)
← 現役期間 →
能力の高さ
手を動かしたら生み
出せる価値の大きさ
解のある表現 :
仮にずっと最後まで訓練した場合
に到達しうる最大能力を H とする。
H の50%、つまり H/2 に能力が到
達するまで訓練期間を維持し、そ
の後、価値を最後の日まで、出力
をし続ければ良い。
H
H/2
図式的に解説すると、冒頭の問題の最適解の
導き方は、理解しやすいと思われます。ただし、
数学的な定式化はやや大変かもしれません。
ひょっとしたら、機械的なアルゴリズムで検証
可能な形で、数学的な証明を書き下すのは、
ひとつ面白い問題だと思います。ç

6. 例題-2
6
前問では、”成長カーブ” は直線であった。
では、その成長カーブを次のように変えた
らどうなるか? (最適な変更点はどこか?)
(1) 平方根関数 t1/2
(1’) 冪指数が α >0 の場合 : tα
(2) 指数関数 exp( β t ) ただし、β>0
ただし、一般性を失わない仮定として、
t の範囲は 0 から 1 とする。
平方根関数
2乗の関数
指数関数 exp(3t)

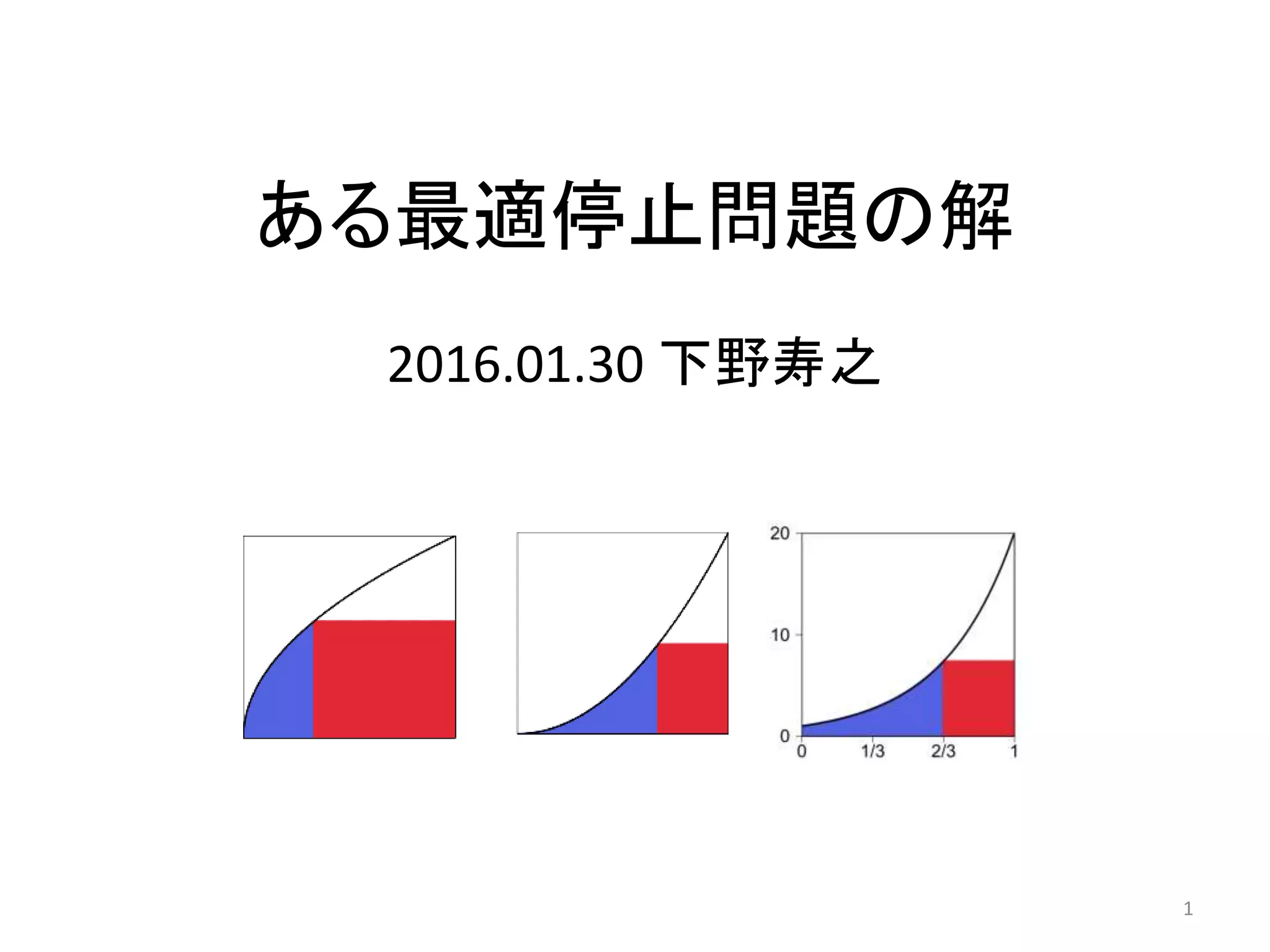
7. 例題-2 の解
7
(1) (1’)
冪指数が固定の場合: h(t) := tα とする(α>0)。
赤の領域の面積は、s := (1-t)tα = tα-tα+1
∴ ds/dt = αtα-1 - (α+1)tα
∴ ds/dt = 0 ⇔ t = α/(α+1) = 1 – 1/(α+1)
従って、
α =1/2 であれば、t=1/3, h(t) = 0.577.. の時点が最適な変更点。
α = 2 であれば、 t=2/3, h(t) = 0.444.. の時点が最適な変更点。
(2) 指数関数の場合 : h(t) := exp( β t ) とする(β>0)。
赤の領域の面積は、s := (1-t)eβt = eβt-teβt
∴ ds/dt = βeβt-(eβt+tβeβt) = (β-1)eβt-βteβt
∴ ds/dt = 0 ⇔ t=(β-1)/β = 1 - 1/β
0≦t≦1の制約により
β >1であれば t = 1-1/β, h(t) = e-1 = 0.367879.. が最適変更点。
β ≦1であれば、t = 0 が最適変更点(青い領域は消失する)。
本題とは関係ありませんが、e3(3) = 20.0855.. で、20からのずれが、たったの0.42..%です。

8. 得られる知見
8
※ 平方根関数は、「”既に身に付けた能力” にちょうど反比
例(-1乗に比例して)、次の1単位の能力の習得に時間がかか
る」をモデリングした微分方程式の解になっている。
横軸は、”成長カーブ”のベキ乗の指
数αを、逆tangent変換したものに対応。
2本の曲線について:
- 細線は T (最適停止時刻)の値
- 太線は h(T) (目標とすべき到達点)
(1) 加速度的/指数関数的に成長できる場合 :
最初はなかなか成長しなくても、
訓練期間は長くする。
ただし、到達可能最高点の約40%で、
あきらめを付けた方が良い。— ???
(2) 成熟後に能力飽和の傾向がある場合:
とりあえず ”達人” の6-7割になれる
までは訓練してみる。
与えられた期間の最初の約30%を
訓練に当てるとよい。
(1)
(2)

9. おまけ
• 密度関数が xα-1(1-x)β-1 /B(α,β) となる [0,1]区間上の確率分布を ベータ
分布と言う。(α,β>0であり、Bはベータ関数。)
• α>1かつβ>1の条件が成り立たないときは、ベータ分布の密度関数の、
対数を取ったものは、上に凸ではない。
• ところが、xをロジット変換( log[x/(1-x)] )したものの密度関数を、対数を
取ると、上に凸になる。
• では、ベータ分布を1変量ではなくて多変量に拡張したディリクレ分布に
ついて、その多変量をどう同時変換したら、密度関数の対数を取ると、
上に凸な関数になるだろうか??
9
本文とは全く脈略無く、
最近思いついた問題です :-)