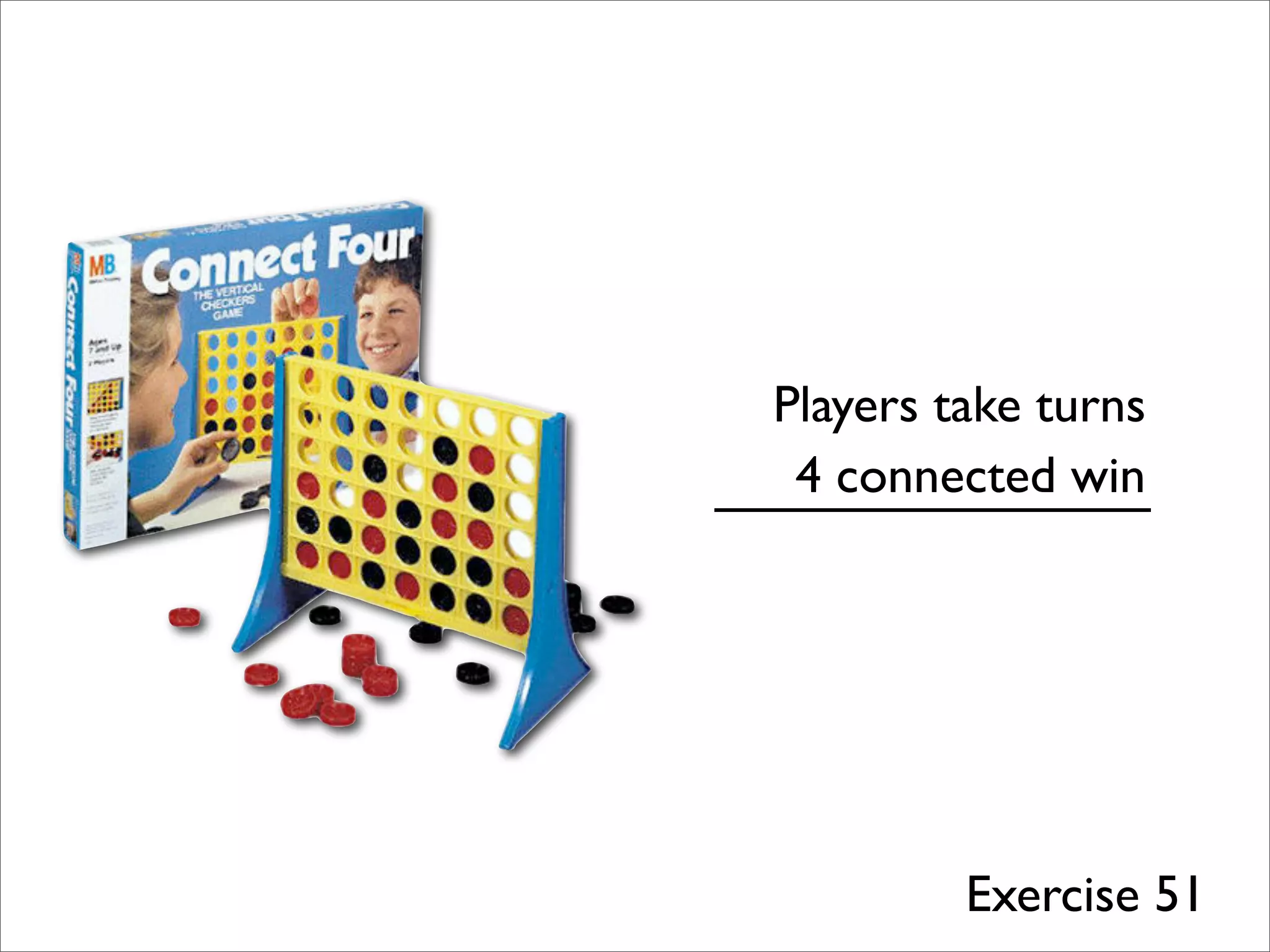
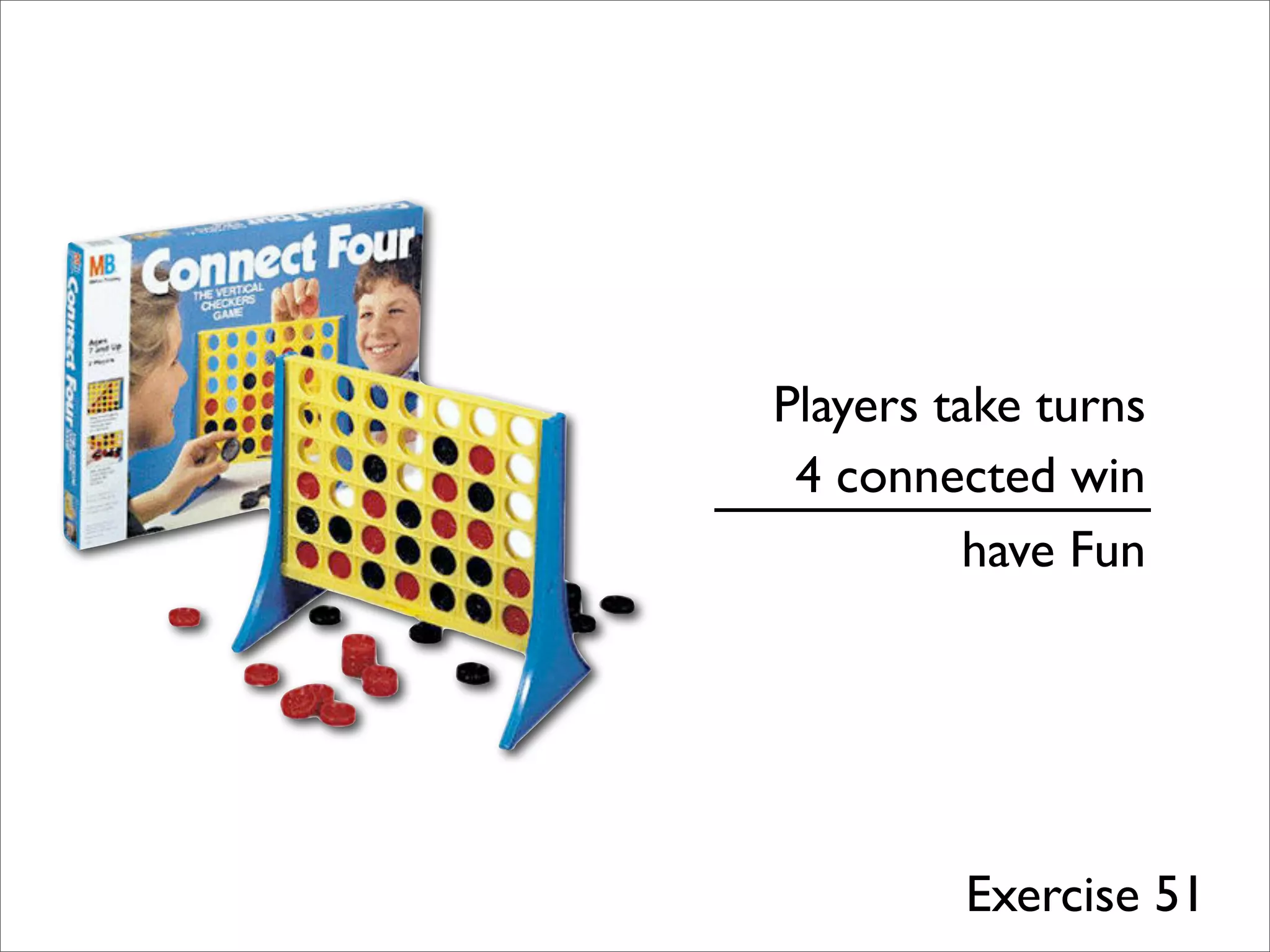
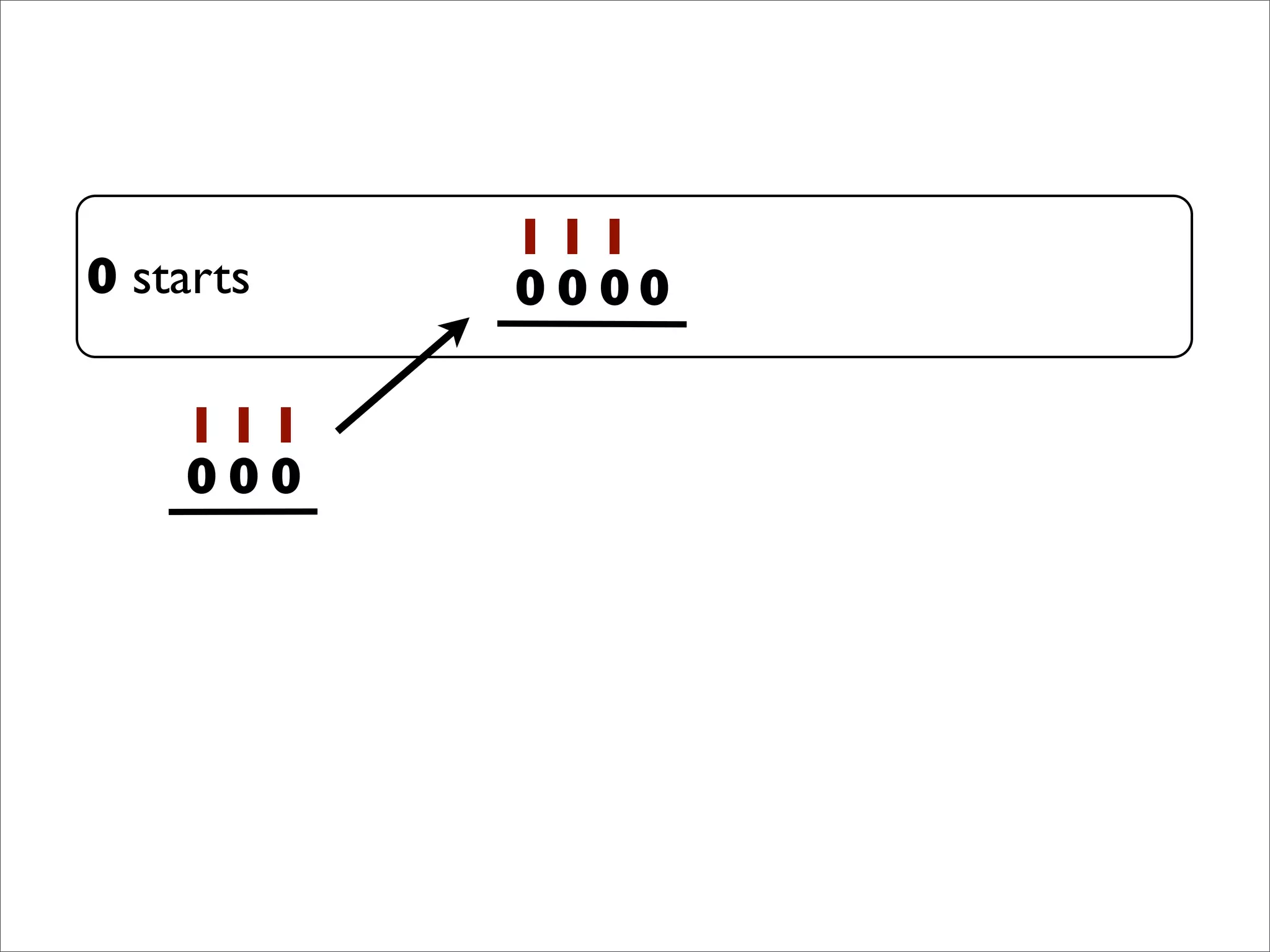
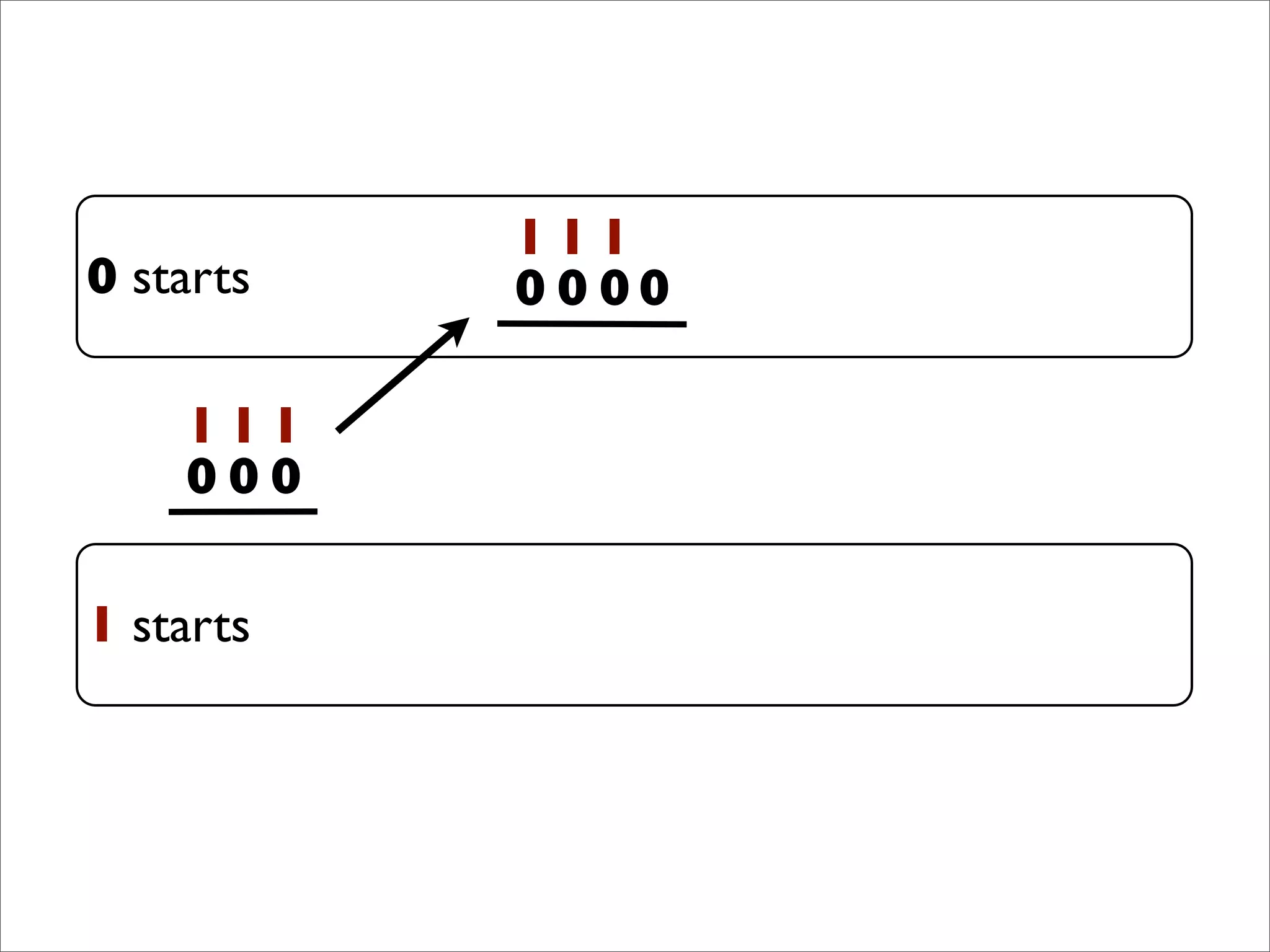
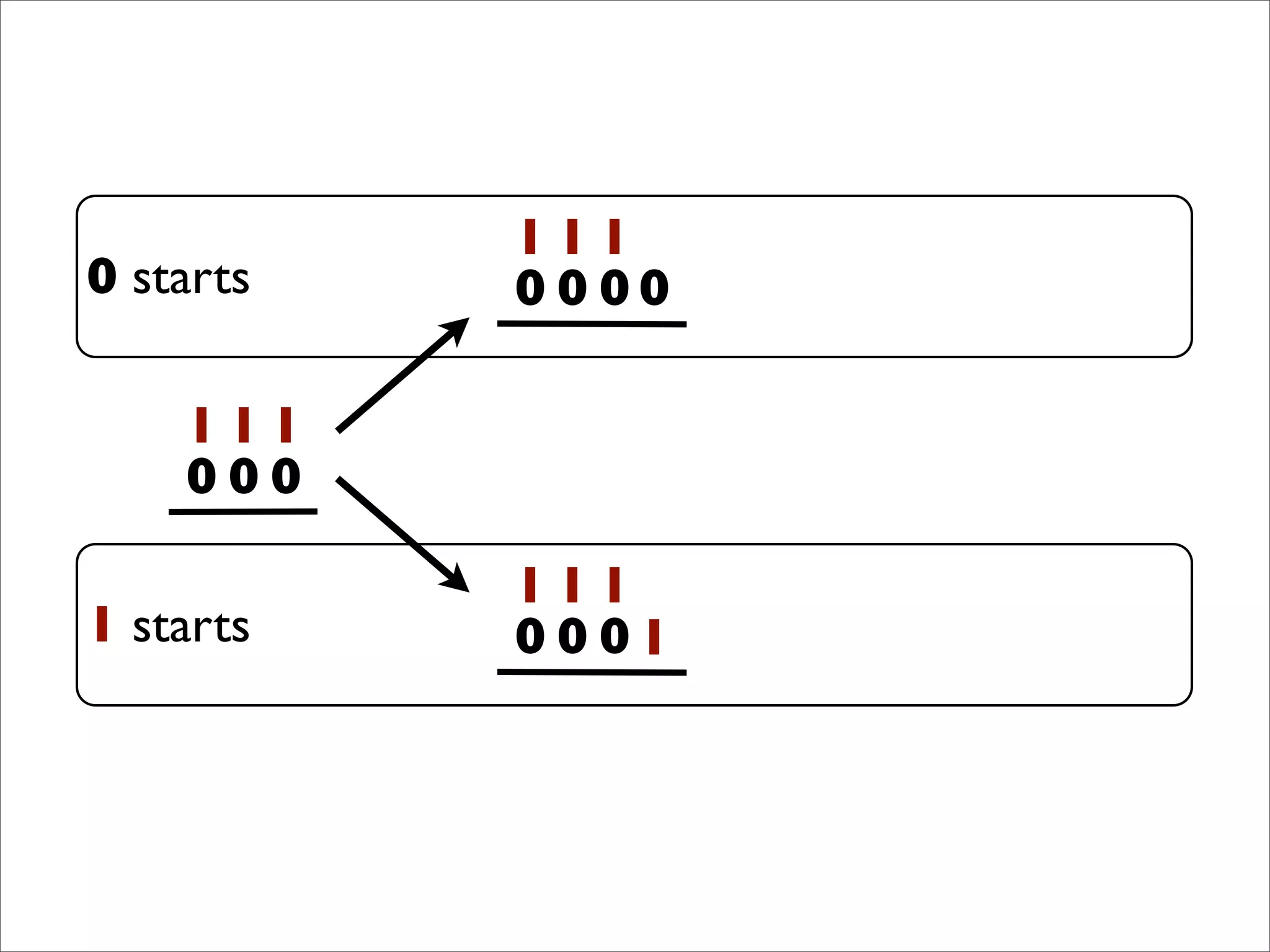
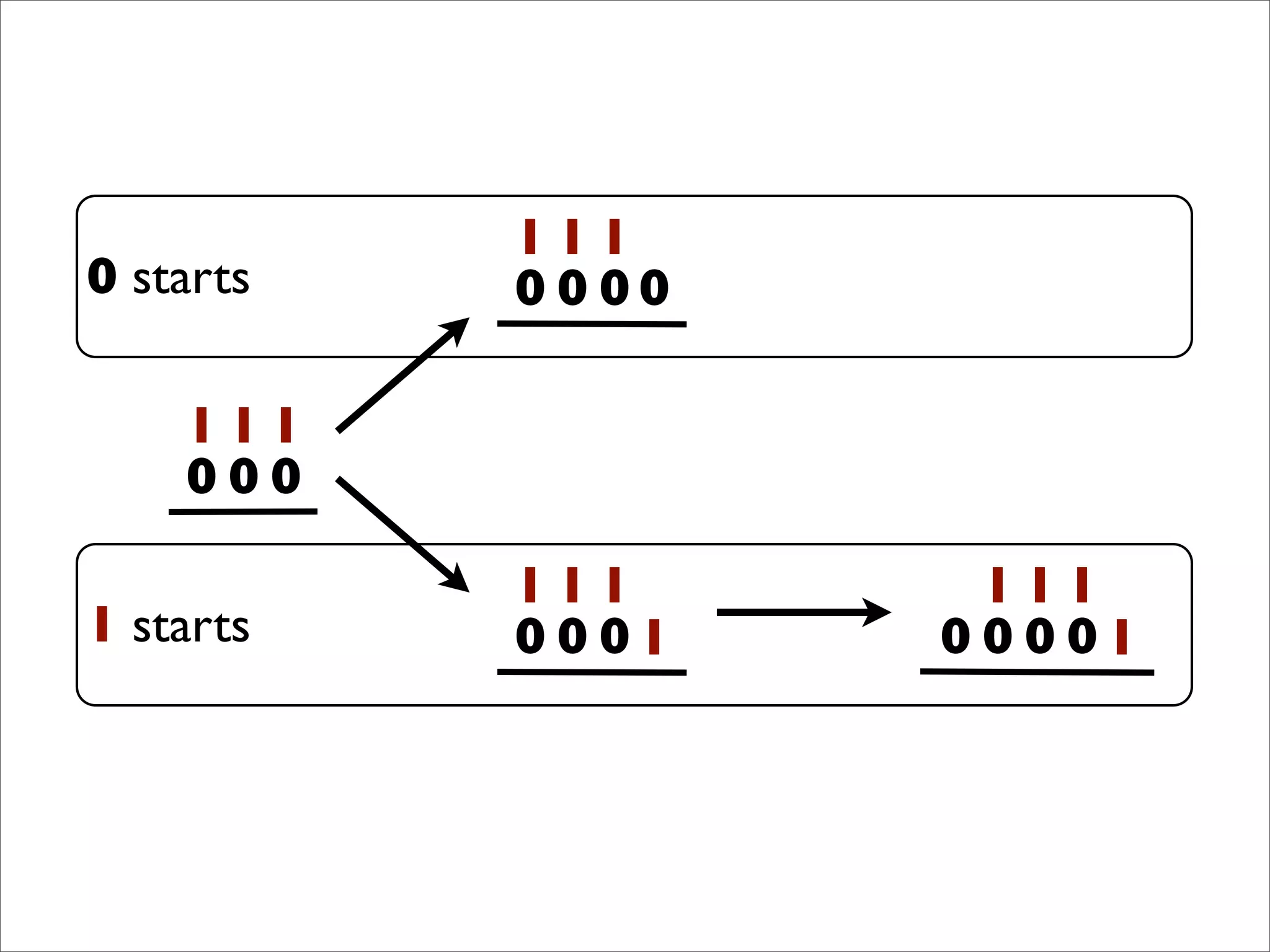
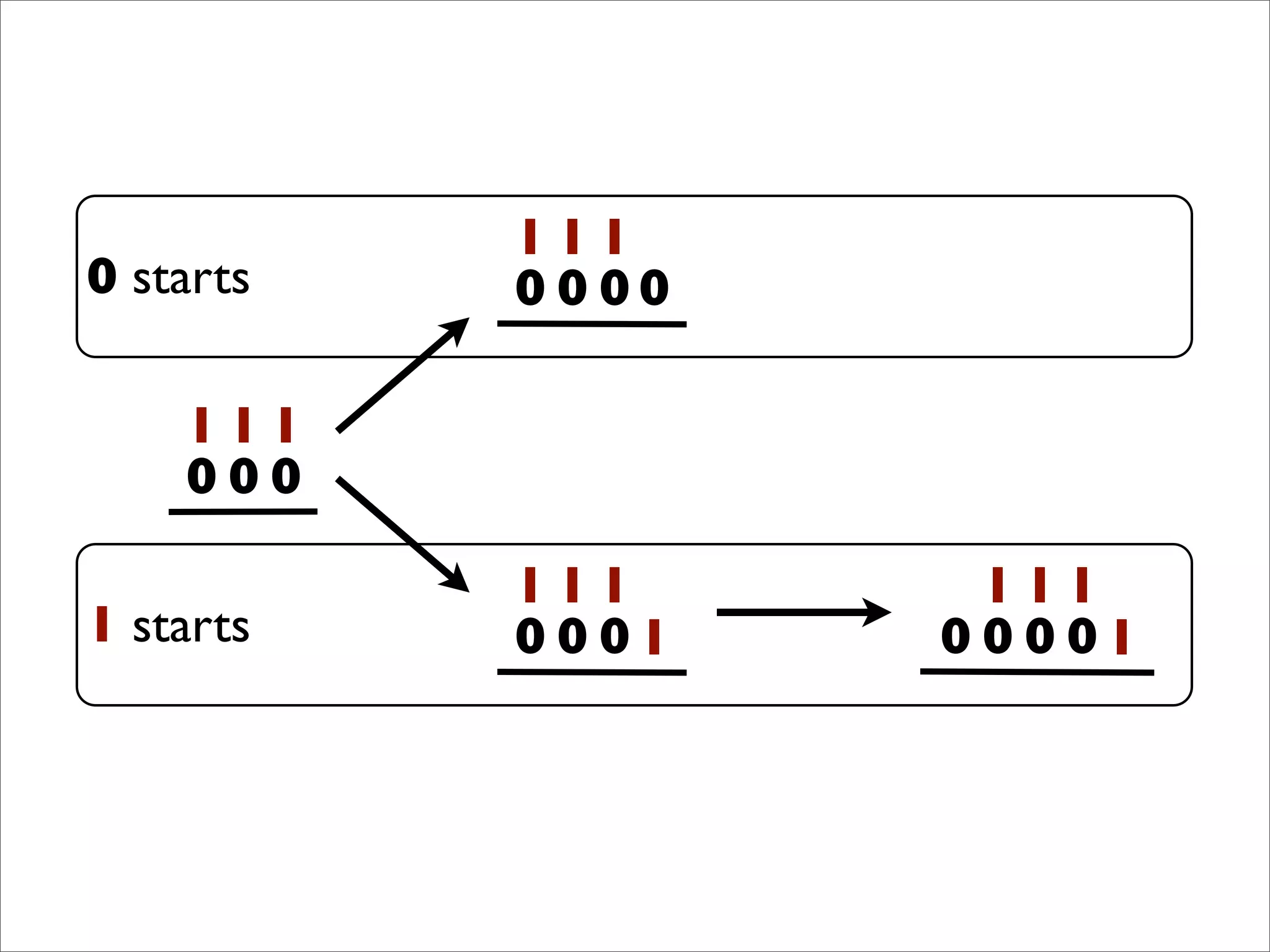
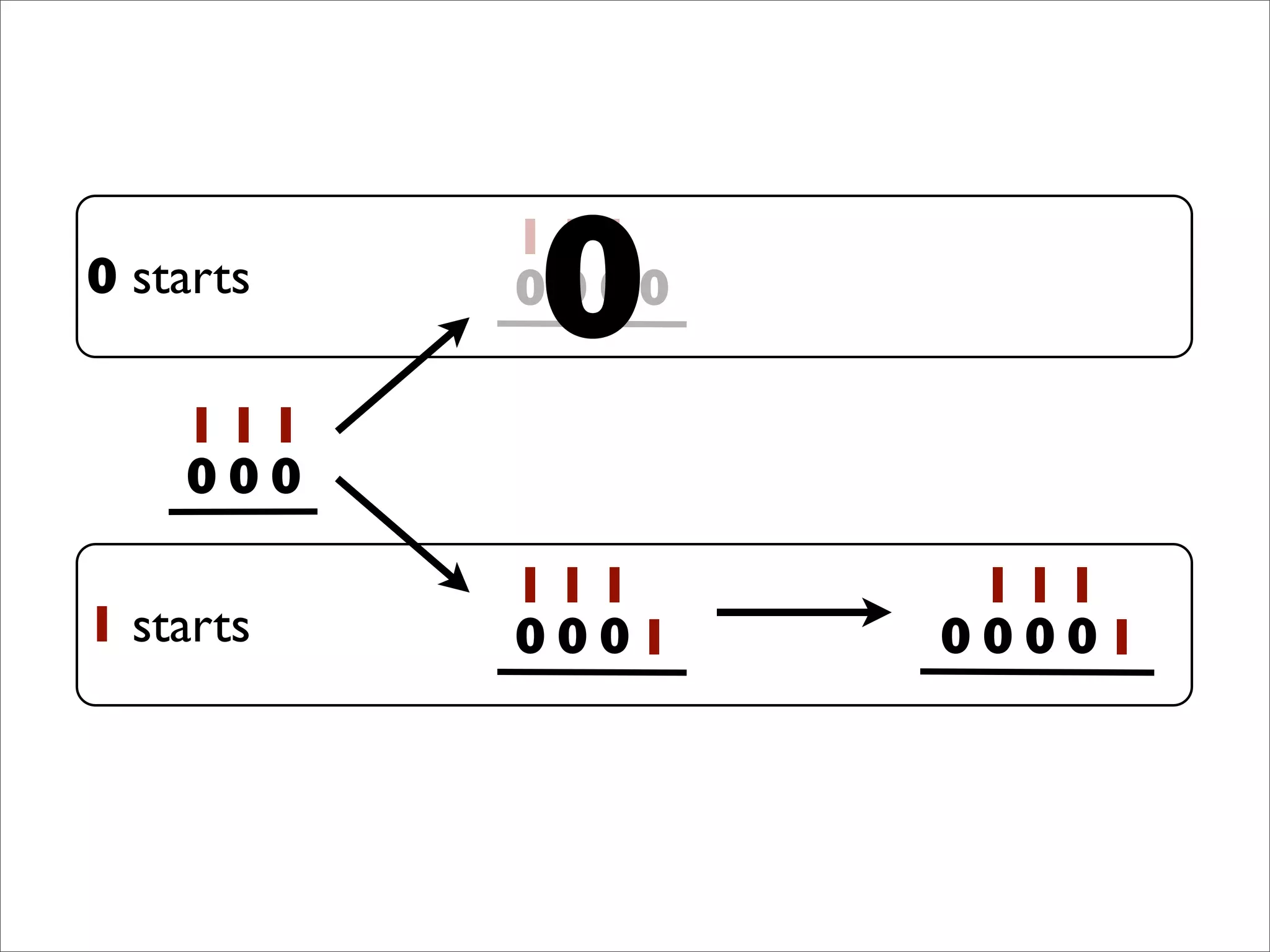
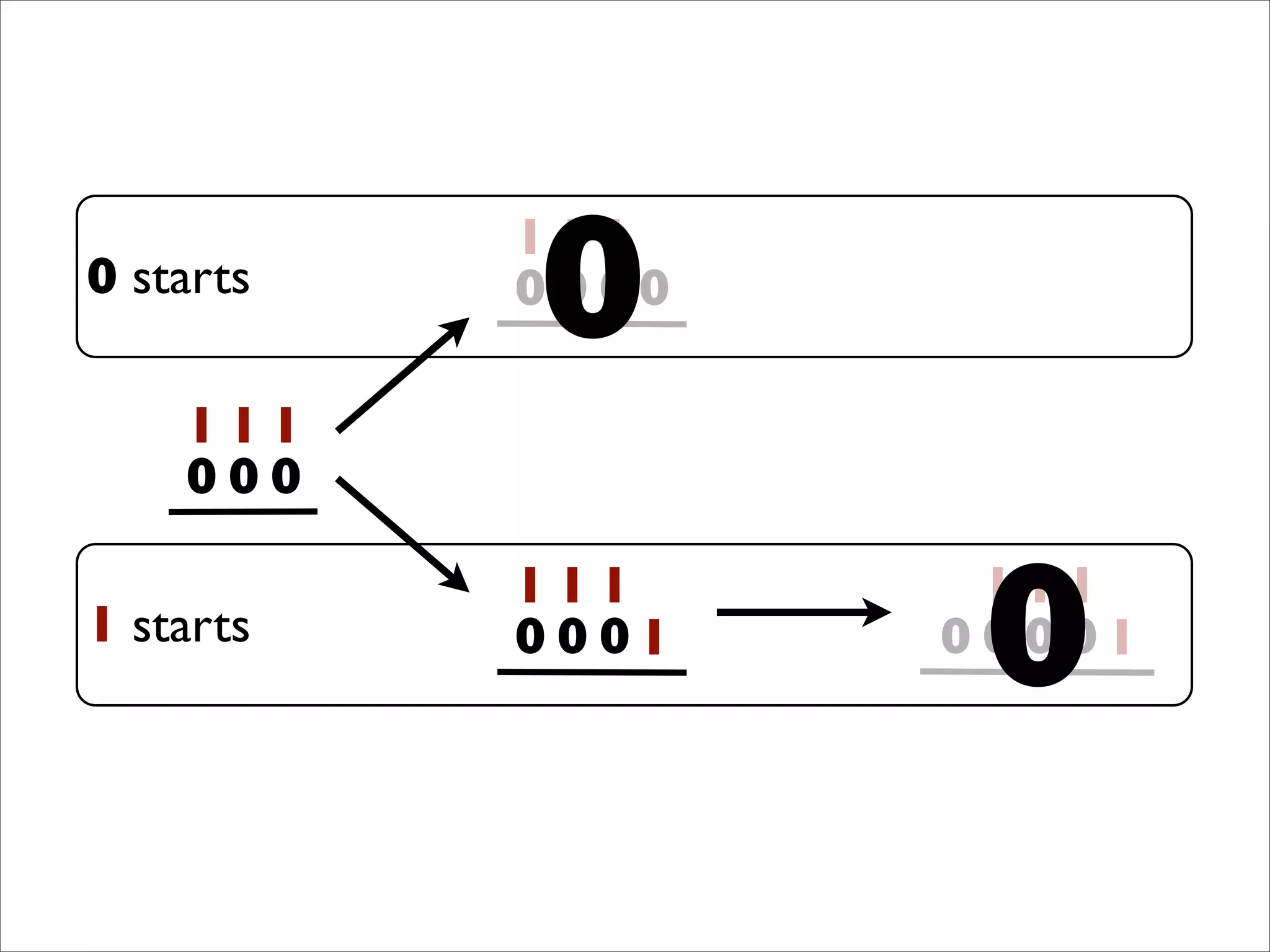
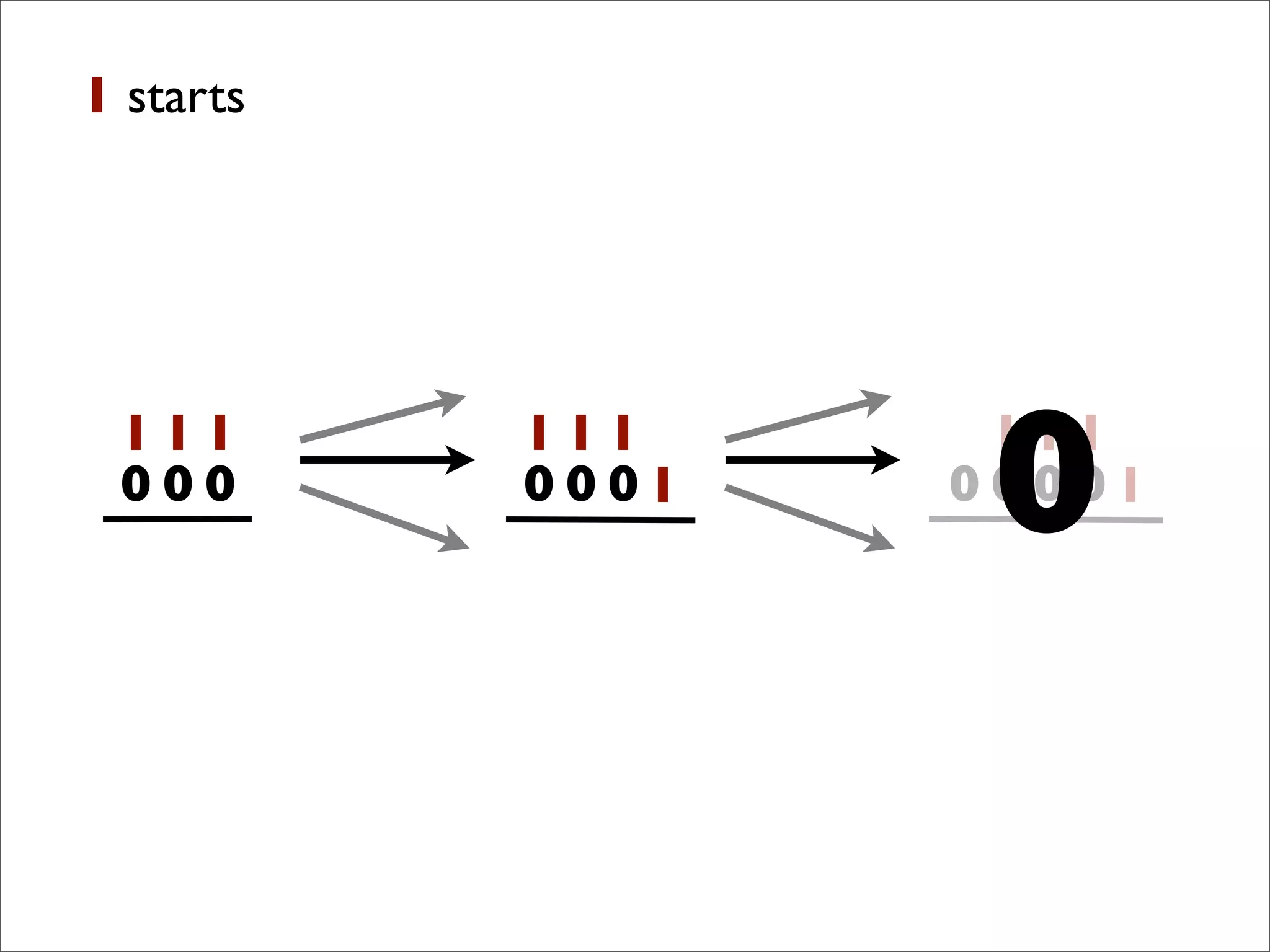
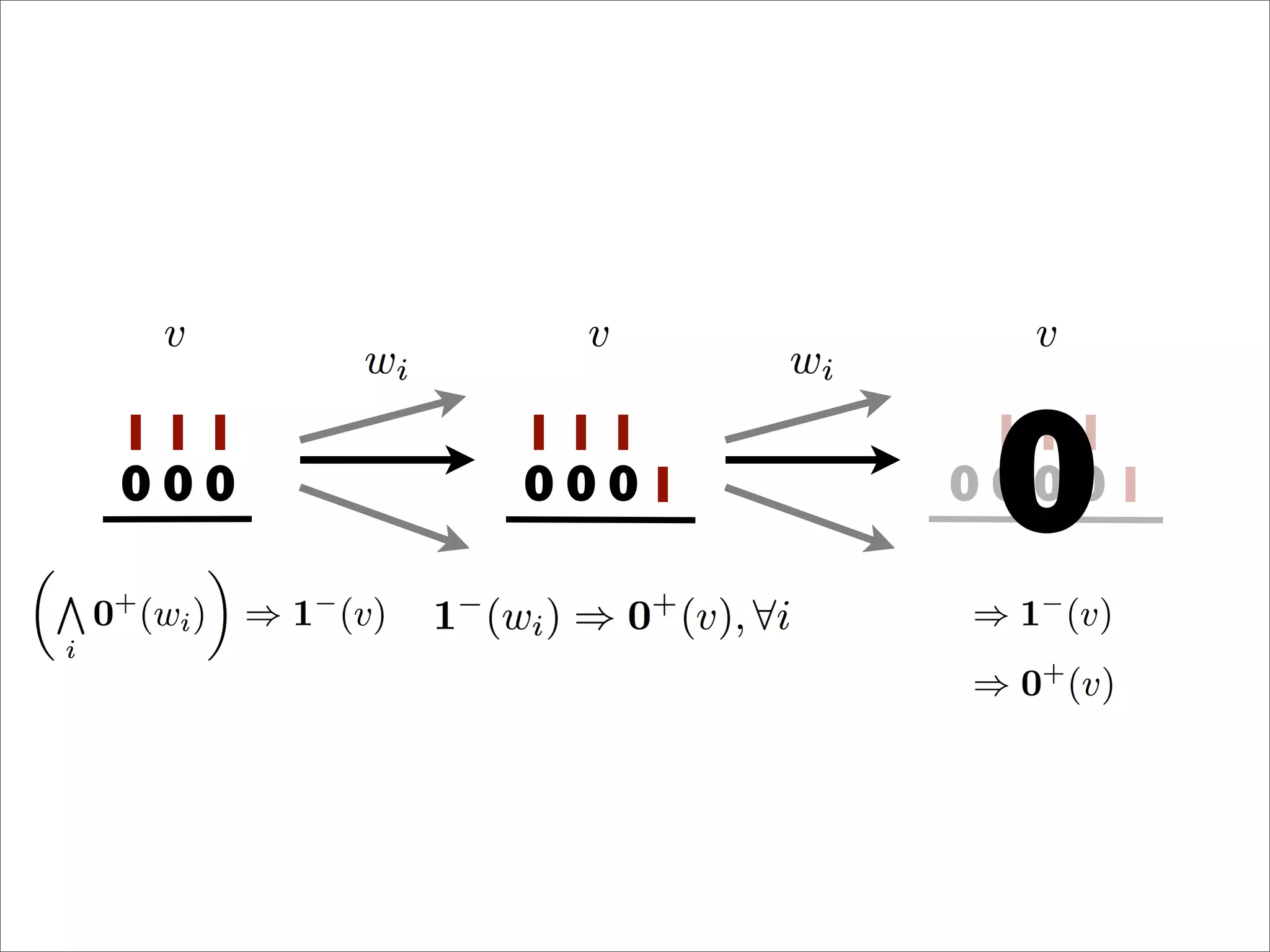
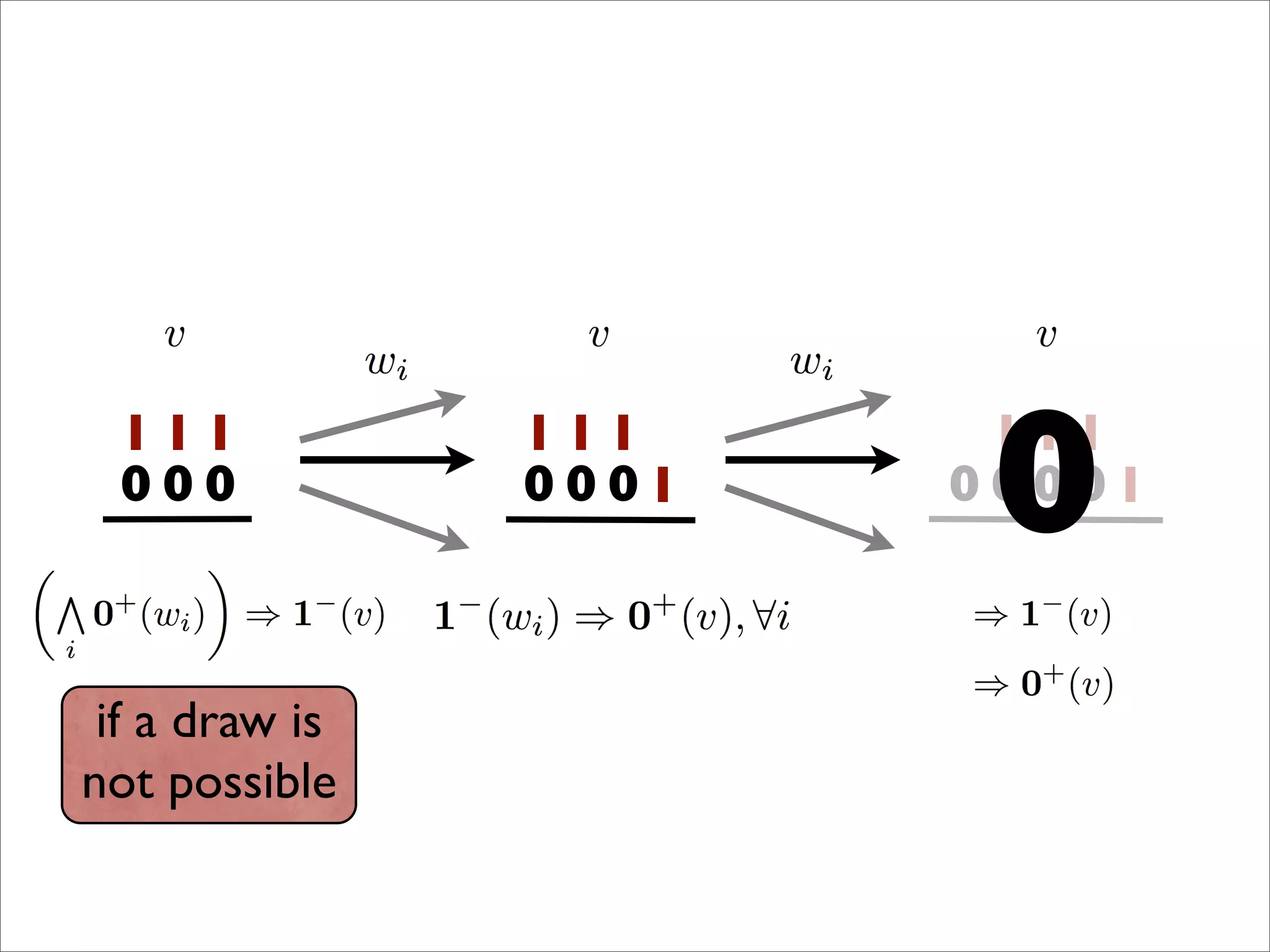
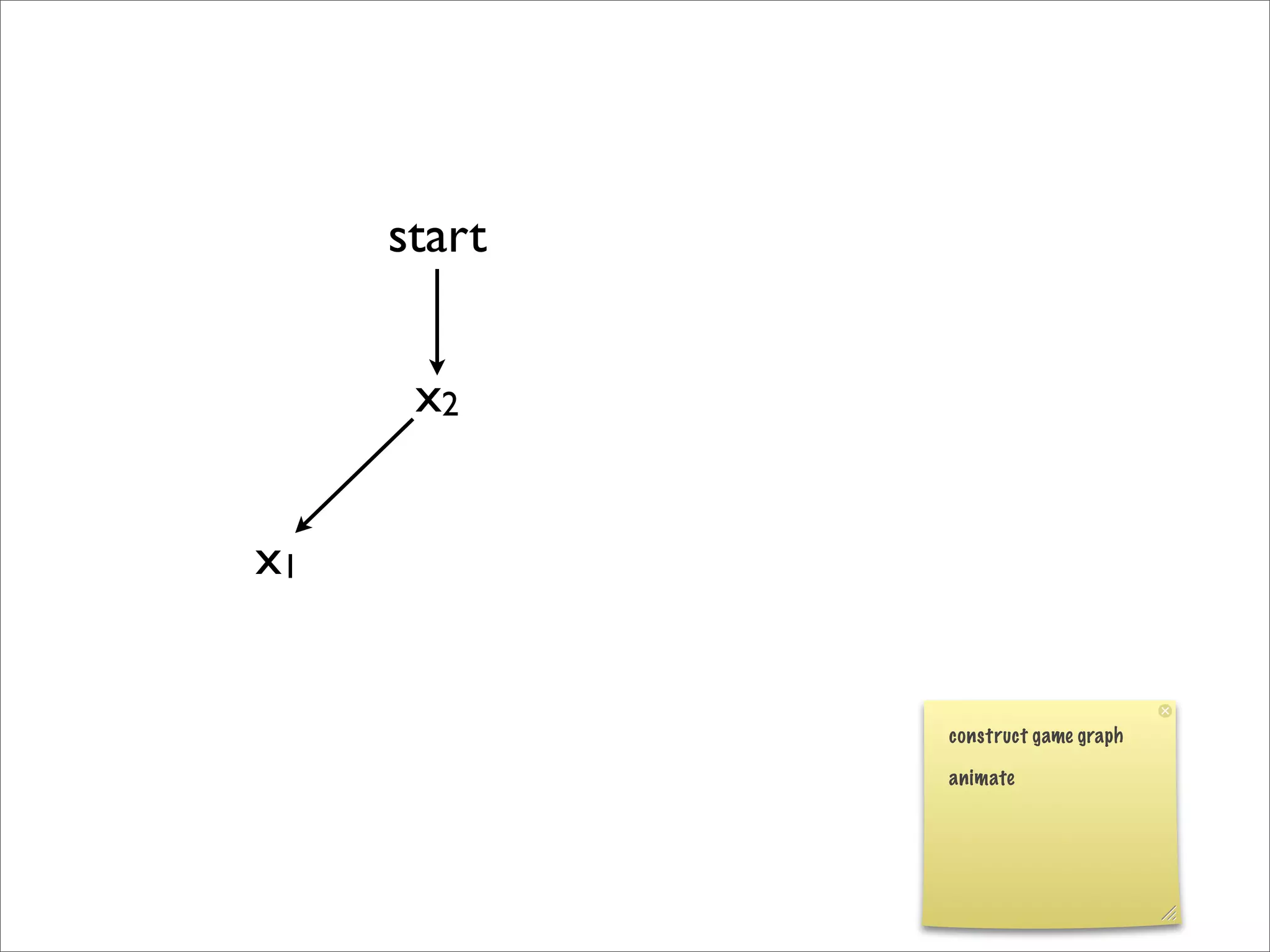
- The document describes Boolean games, which are turn-based, one-on-one games between two players. - Players take turns selecting values (0 or 1) that are added to the game board. The first player to get four values in a connected row wins. - The document discusses generalizing Boolean games and constructing a graph representation of games. It also provides examples of different Boolean functions that define the rules and outcomes of games with varying numbers of positions.

1. 1vs.
Boolean Games
turn based, one on one

2. Exercise 51

3. Players take turns
Exercise 51

4. Players take turns
4 connected win
Exercise 51

5. Players take turns
4 connected win
Exercise 51

6. have Fun
Players take turns
4 connected win
Exercise 51

8. 1
0
1
0
1
0

9. 1
0
1
0
1
0
0 starts

10. 1
0
1
0
1
0
1
0
1
0
1
0 00 starts

11. 1
0
1
0
1
0
1
0
1
0
1
0 0
1 starts
0 starts

12. 1
0
1
0
1
0
1
0
1
0
1
0 0
1
0
1
0
1
0 11 starts
0 starts

13. 1
0
1
0
1
0
1
0
1
0
1
0 0
1
0
1
0
1
0 1
1
0
1
0
1
0 101 starts
0 starts

14. Task: construct a set of Horn clauses that
describe if a player has already won
or lost.

15. 1
0
1
0
1
0
1
0
1
0
1
0 0
1
0
1
0
1
0 1
1
0
1
0
1
0 101 starts
0 starts

16. 1
0
1
0
1
0
1
0
1
0
1
0 0
1
0
1
0
1
0 1
1
0
1
0
1
0 101 starts
0 starts
0

17. 1
0
1
0
1
0
1
0
1
0
1
0 0
1
0
1
0
1
0 1
1
0
1
0
1
0 101 starts
0 starts
0
0

18. 1
0
1
0
1
0
1
0
1
0
1
0 1
1
0
1
0
1
0 10
1 starts
0

19. 1
0
1
0
1
0
1
0
1
0
1
0 1
1
0
1
0
1
0 10
1 starts
0

20. 1
0
1
0
1
0
1
0
1
0
1
0 1
1
0
1
0
1
0 10
1 starts
0

21. 1
0
1
0
1
0
1
0
1
0
1
0 1
1
0
1
0
1
0 10
1 starts
0

22. How can we generalize?

23. 1
0
1
0
1
0
1
0
1
0
1
0 1
1
0
1
0
1
0 10
0

24. 1
0
1
0
1
0
1
0
1
0
1
0 1
1
0
1
0
1
0 10
0

25. 1
0
1
0
1
0
1
0
1
0
1
0 1
1
0
1
0
1
0 10
0
if a draw is
not possible

26. 00001110001000110000111000001100011100001110000001
10001000011000110000110000011000001000110000001000
00111000000111000100011000011100000110001110000111
00000011000100001100011000011000001100000100011000
00010000011100000011100010001100001110000011000111
00001110001000110001000011000110000110000011000001
00011000000100000111000000111000100011000011100000
11000111000011100000011000100001100011000011000001
10000010001100000010000011100000011100010001100001
11000001100011100001110000001100010000110001100001
10000011000001000110000001000001110000001110001000
11000011100000110001110000111000000110001000011000
11000011001000110000010001100002001000001110000001
11000100011000011100000110001110000111000000110001
00001100011000011000001100000100011000000100000111
00000011100010001100001110000011000111000011100000
“Any Boolean function leads to
a Game ...”
Donald E. Knuth
Exercise 52

27. construct game graph
animate
x2
start

28. construct game graph
animate
x2
x1
start

29. construct game graph
animate
x2
x1
x4
start

30. construct game graph
animate
x2
x3 x5 x7
x6 x8
x9x1
x4
start

31. x1 x3 x5 x7
x6x4 x8
x9
1
some example steps
- max 4 possible moves
-
start

32. x1 x3 x5 x7
x6 x8
x9
1 0
some example steps
- max 4 possible moves
-
start

33. x1 x5 x7
x6 x8
x9
1 0
1
some example steps
- max 4 possible moves
-
start

34. x1 x5 x7
x6 x8
x9
0
1
0
some example steps
- max 4 possible moves
-
start

35. x1
x2

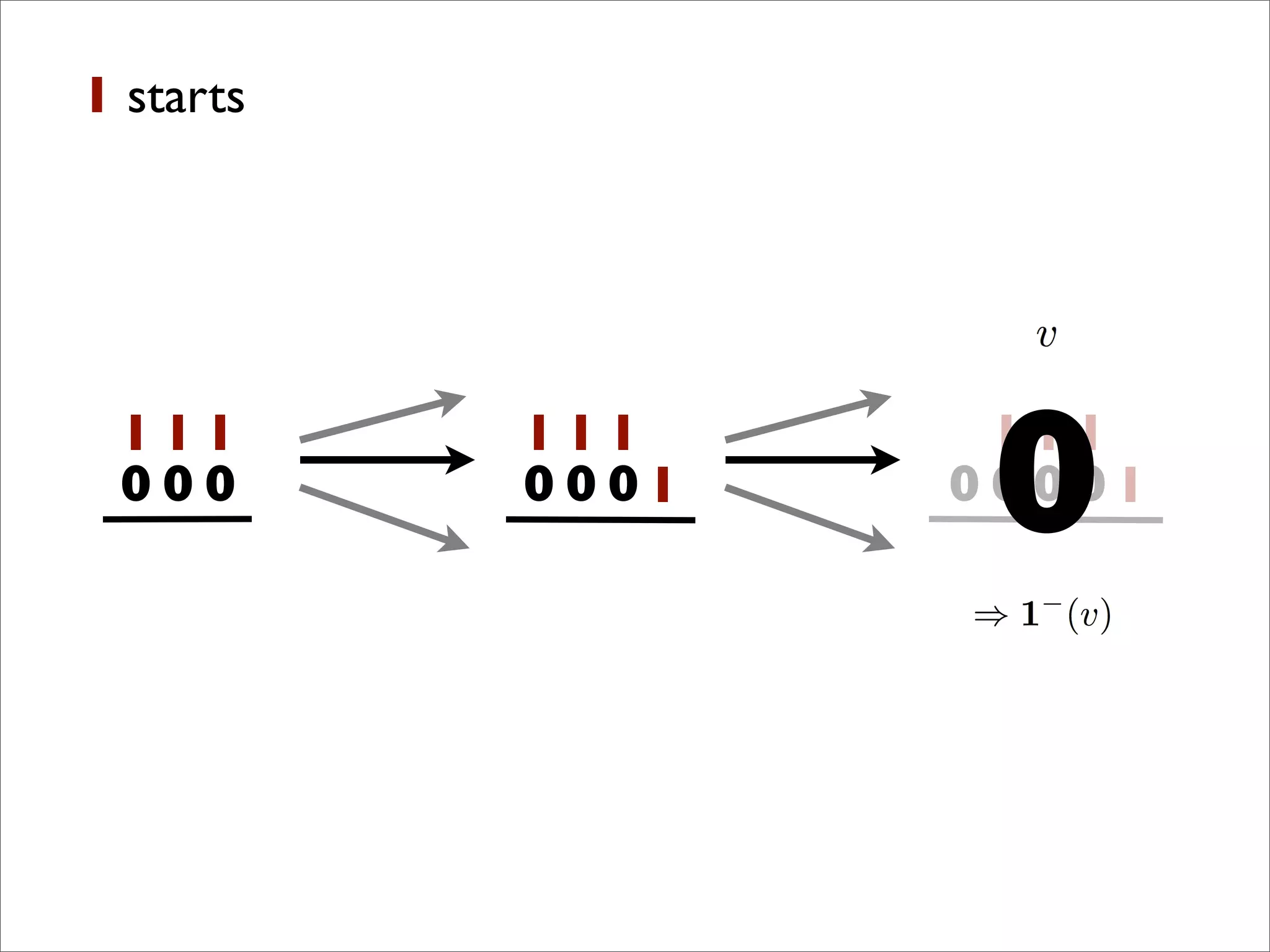
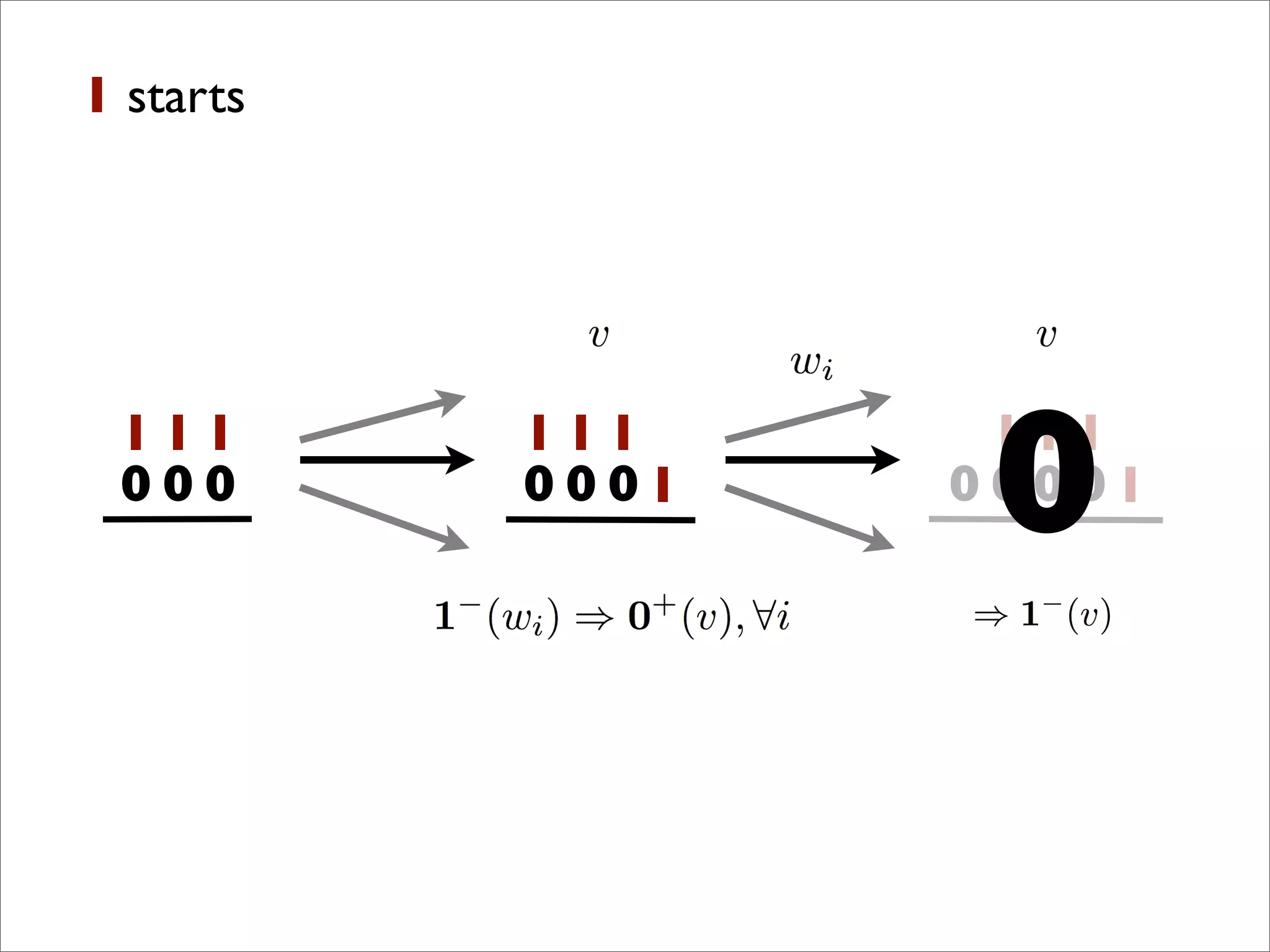
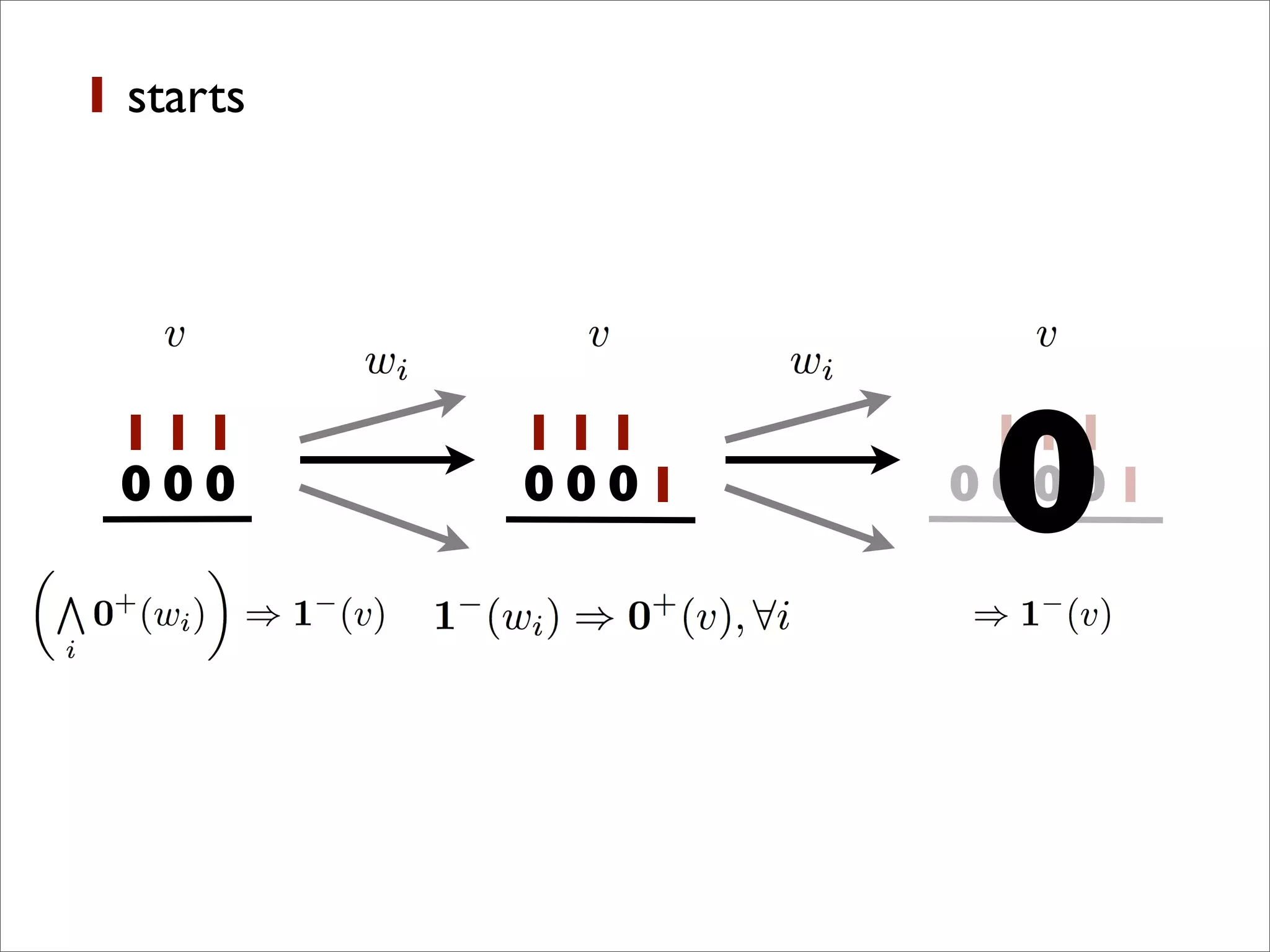
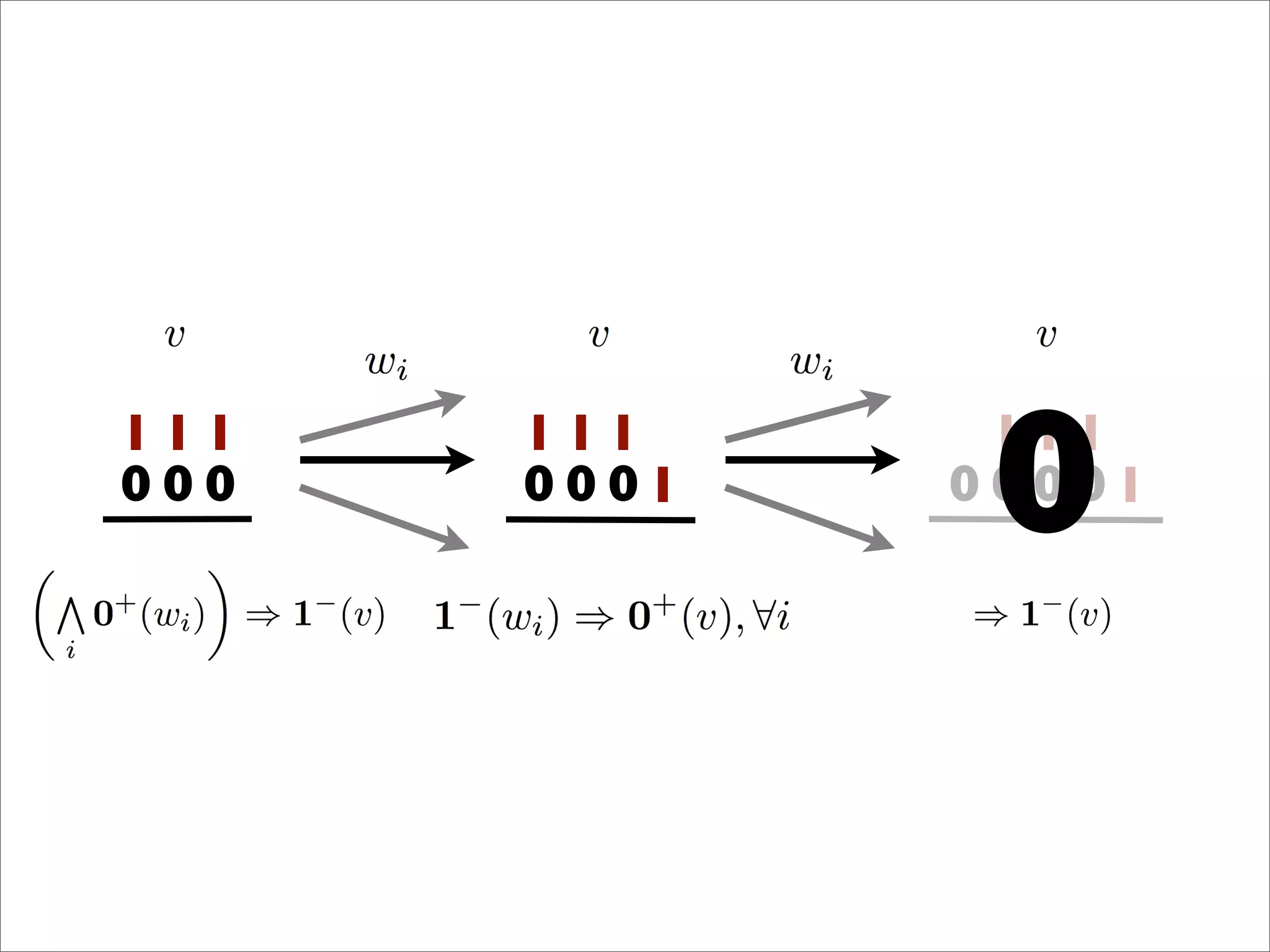
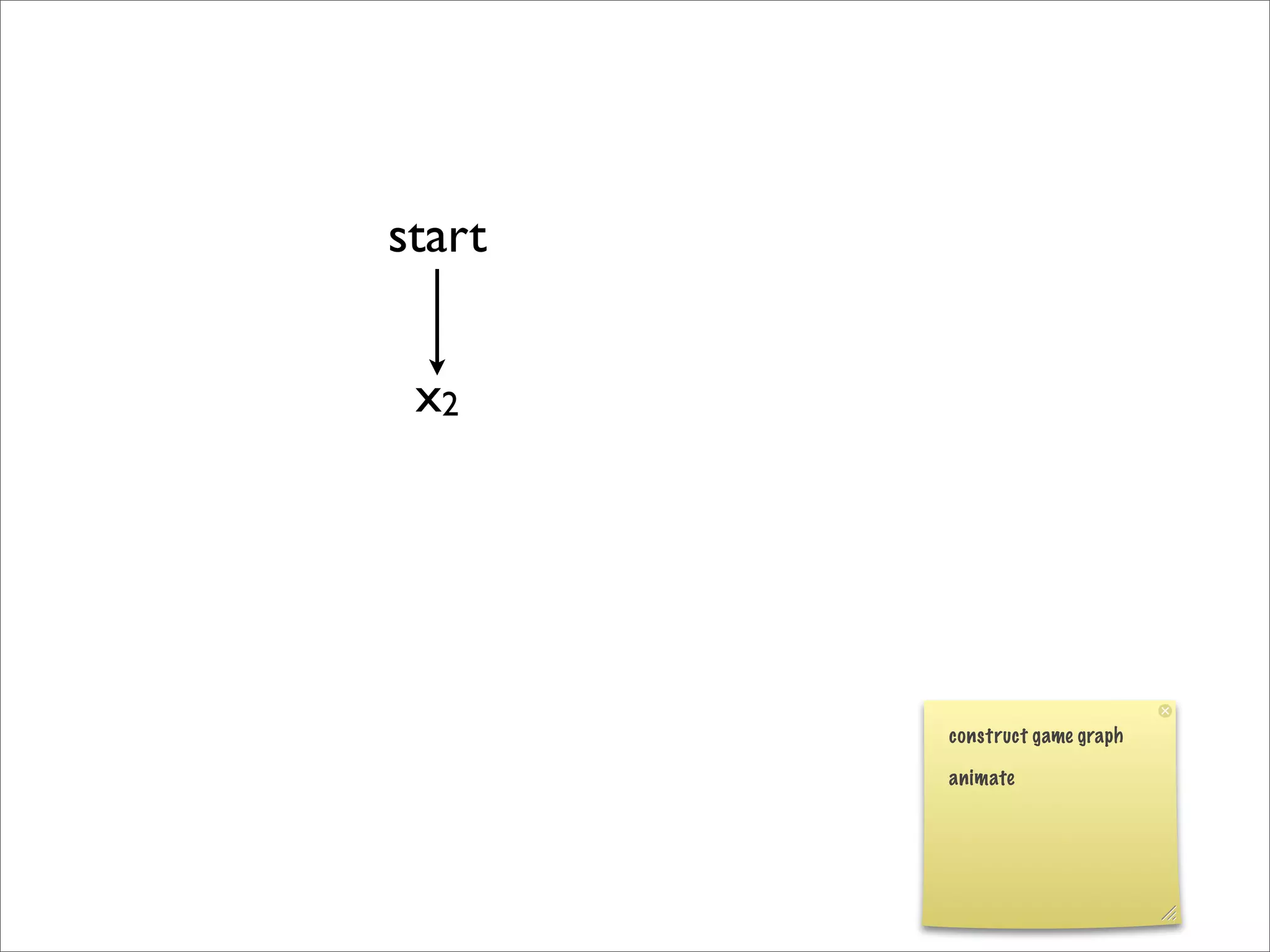
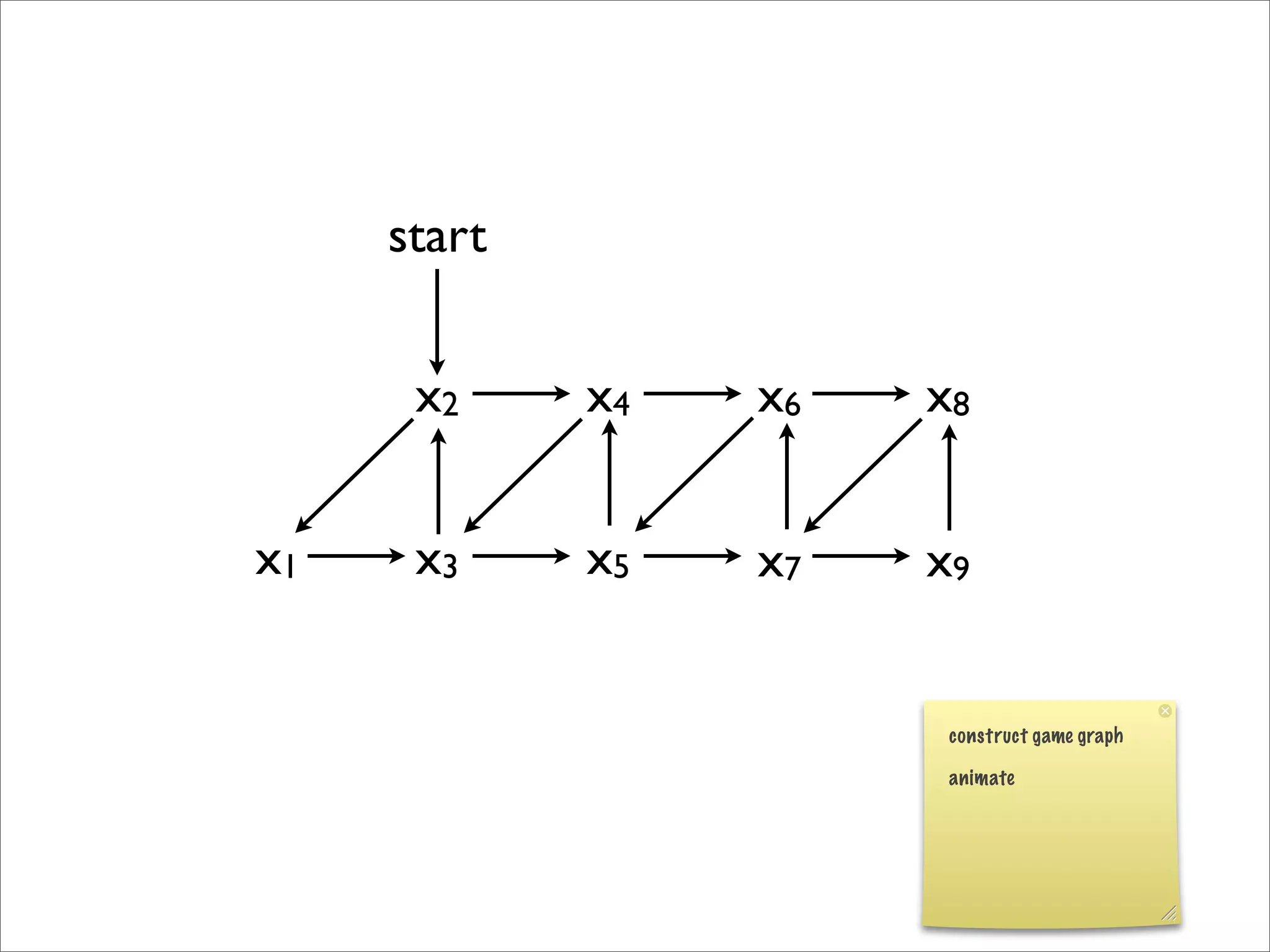
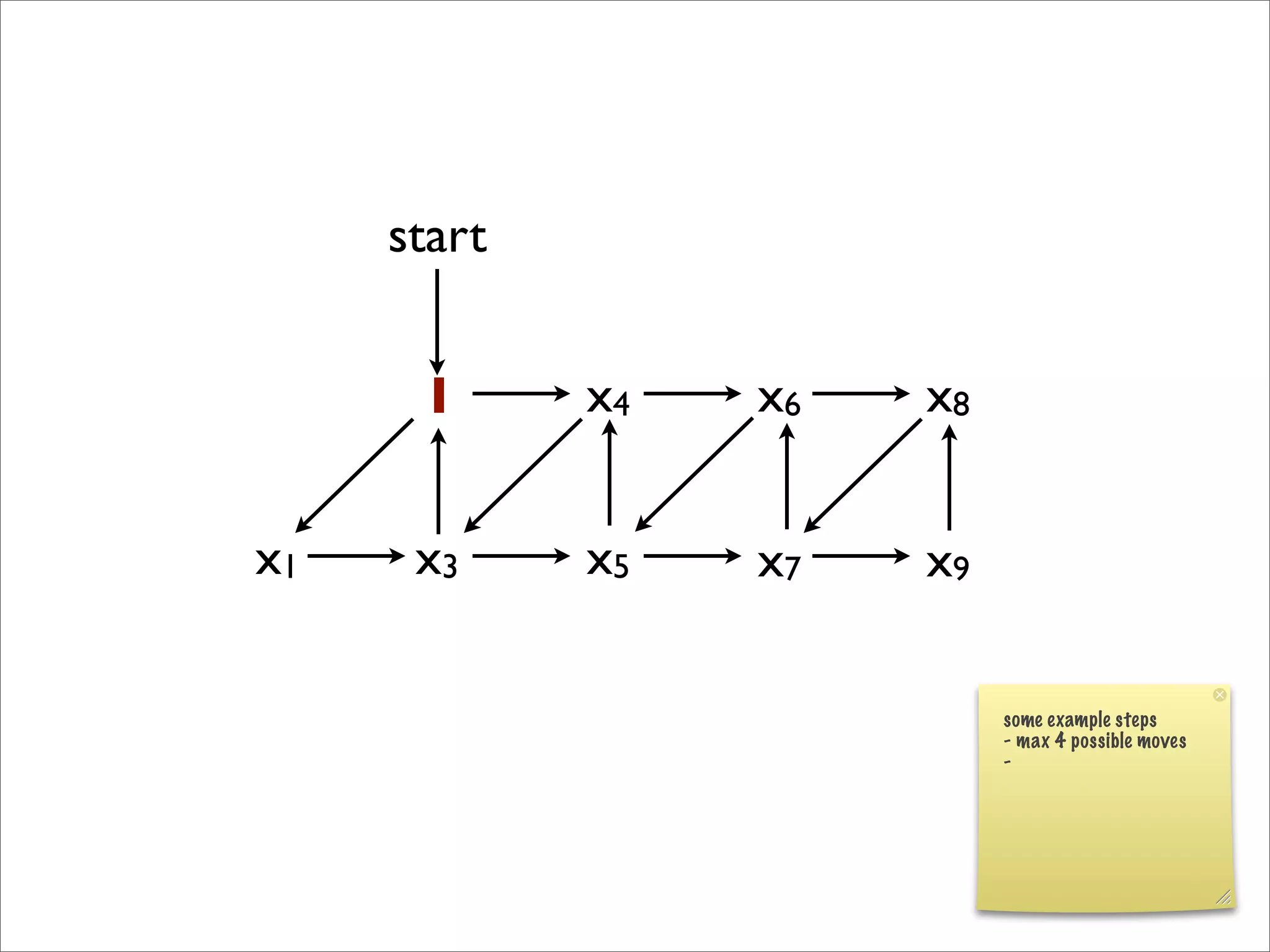
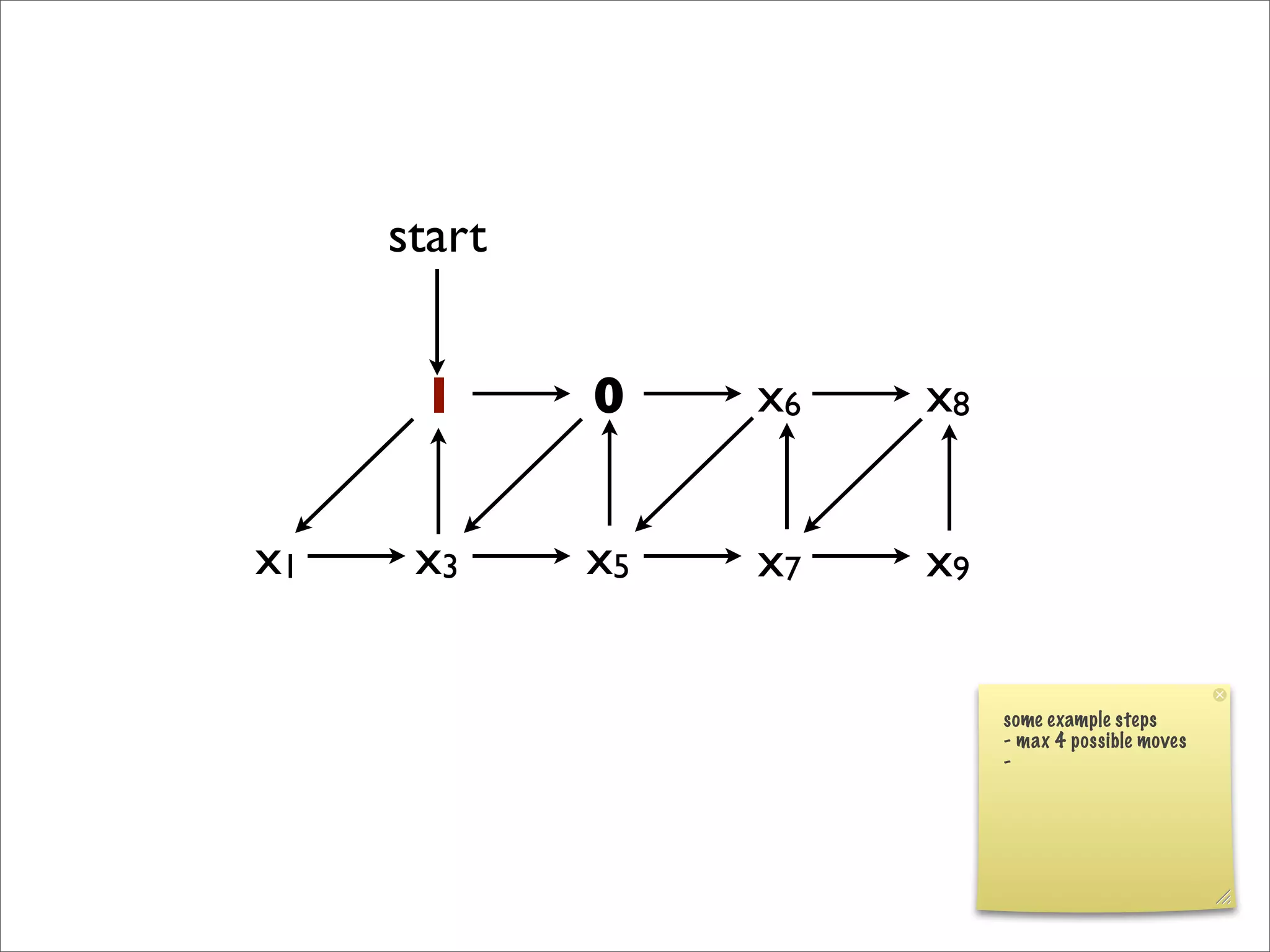
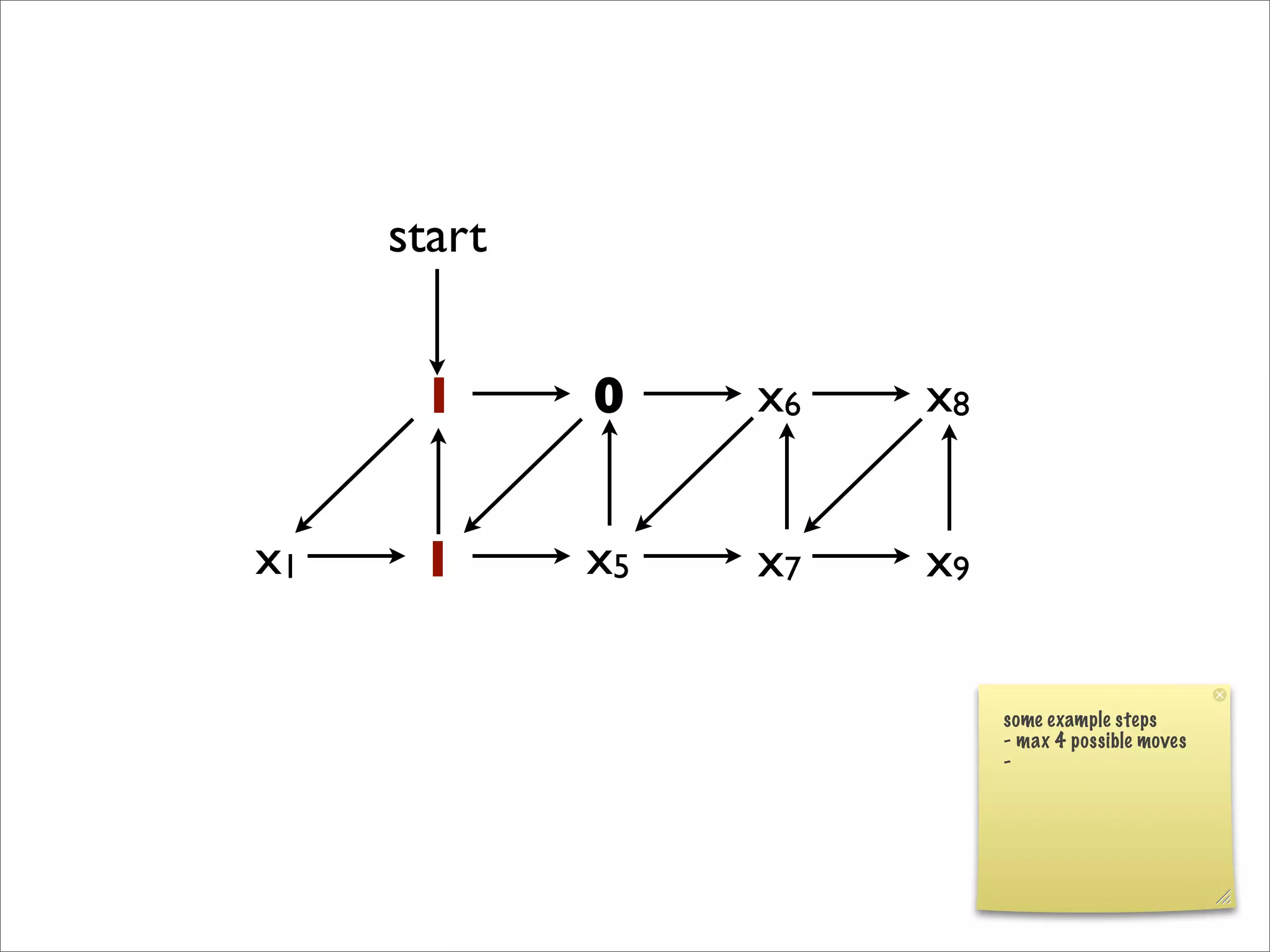
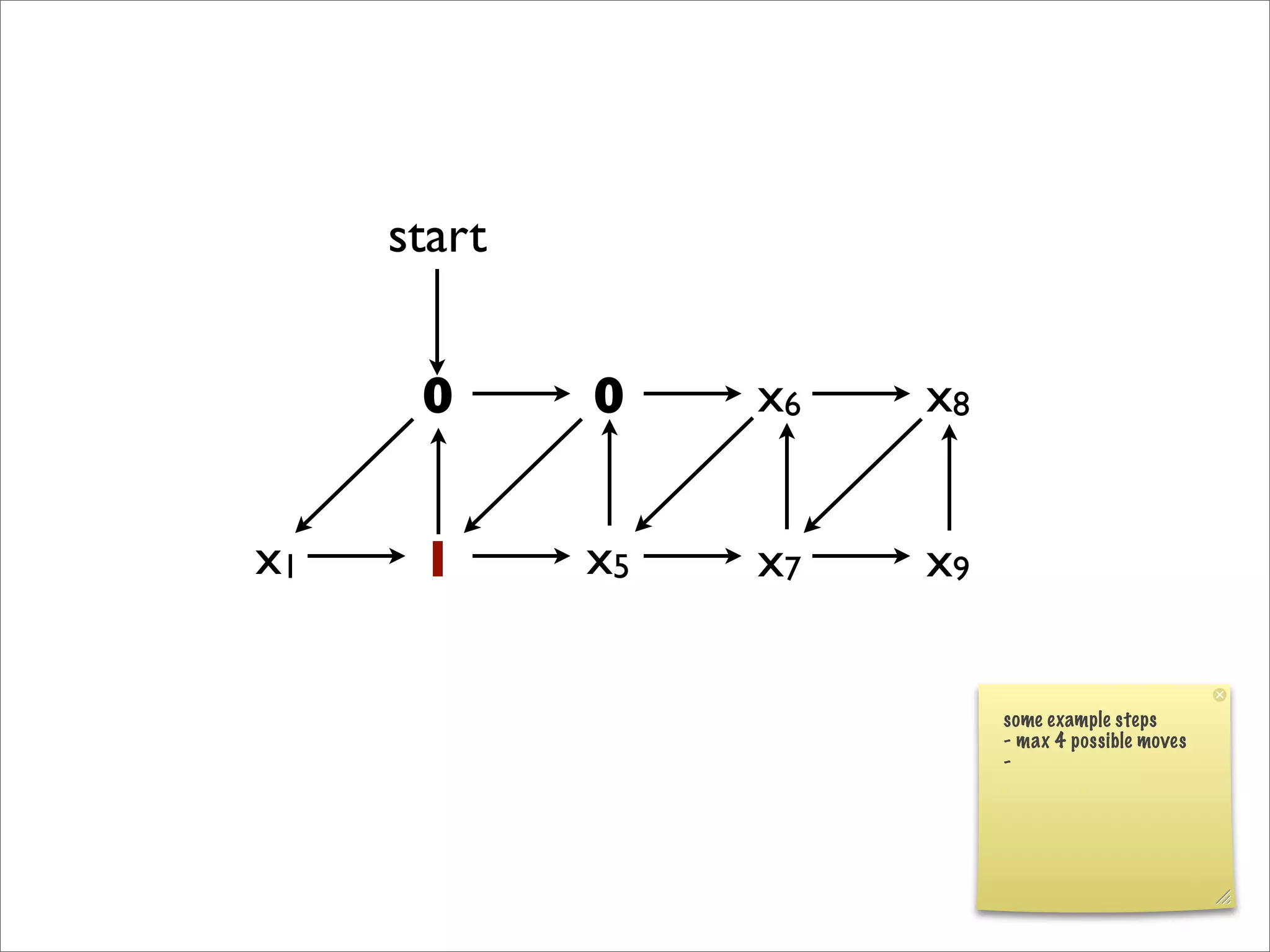
36. x1
x2
(a) f(x[1:n]) = x[1:n] < x[n:1]╓
╙
╓
╙

37. x1
x2
xx
(a) f(x[1:n]) = x[1:n] < x[n:1]╓
╙
╓
╙

38. x1
x2
xx
x0
x1
(a) f(x[1:n]) = x[1:n] < x[n:1]╓
╙
╓
╙

39. x1
x2
xx
x0
x1
00
10
01
11
(a) f(x[1:n]) = x[1:n] < x[n:1]╓
╙
╓
╙

40. x1
x2
xx
x0
x1
0
0
0
1
(a) f(x[1:n]) = x[1:n] < x[n:1]╓
╙
╓
╙

41. x1
x2
xx
x1
0
0
0
1
0
(a) f(x[1:n]) = x[1:n] < x[n:1]╓
╙
╓
╙

42. Algorithm C

43. n (a)
2 0 wins
3 0 wins
4 first wins
5 second wins
6 second wins
7 1 loses if first
8 draw
9 draw
(a) f(x[1:n]) = x[1:n] < x[n:1]╓
╙
╓
╙

44. n (b)
2 second wins
3 first wins
4 first wins
5 draw
6 second wins
7 second wins
8 draw
9 draw
(b) f(x[1:n]) = xi⊕i

45. n (c)
2 1 wins
3 first wins
4 first wins
5 draw
6 1 loses if first
7 1 loses if first
8 draw
9 draw
(c) f(x[1:n]) = x[1:n] contains
no two consecutive 1’s
╓
╙ ╓
╙

46. n (d)
2 second wins
3 first wins
4 first wins
5 1 loses if first
6 1 loses if first
7 1 loses if first
8 1 loses if first
9 1 loses if first
(d) f(x[1:n]) = (x[1:n])2 is prime╓
╙
╓
╙

47. Questions?