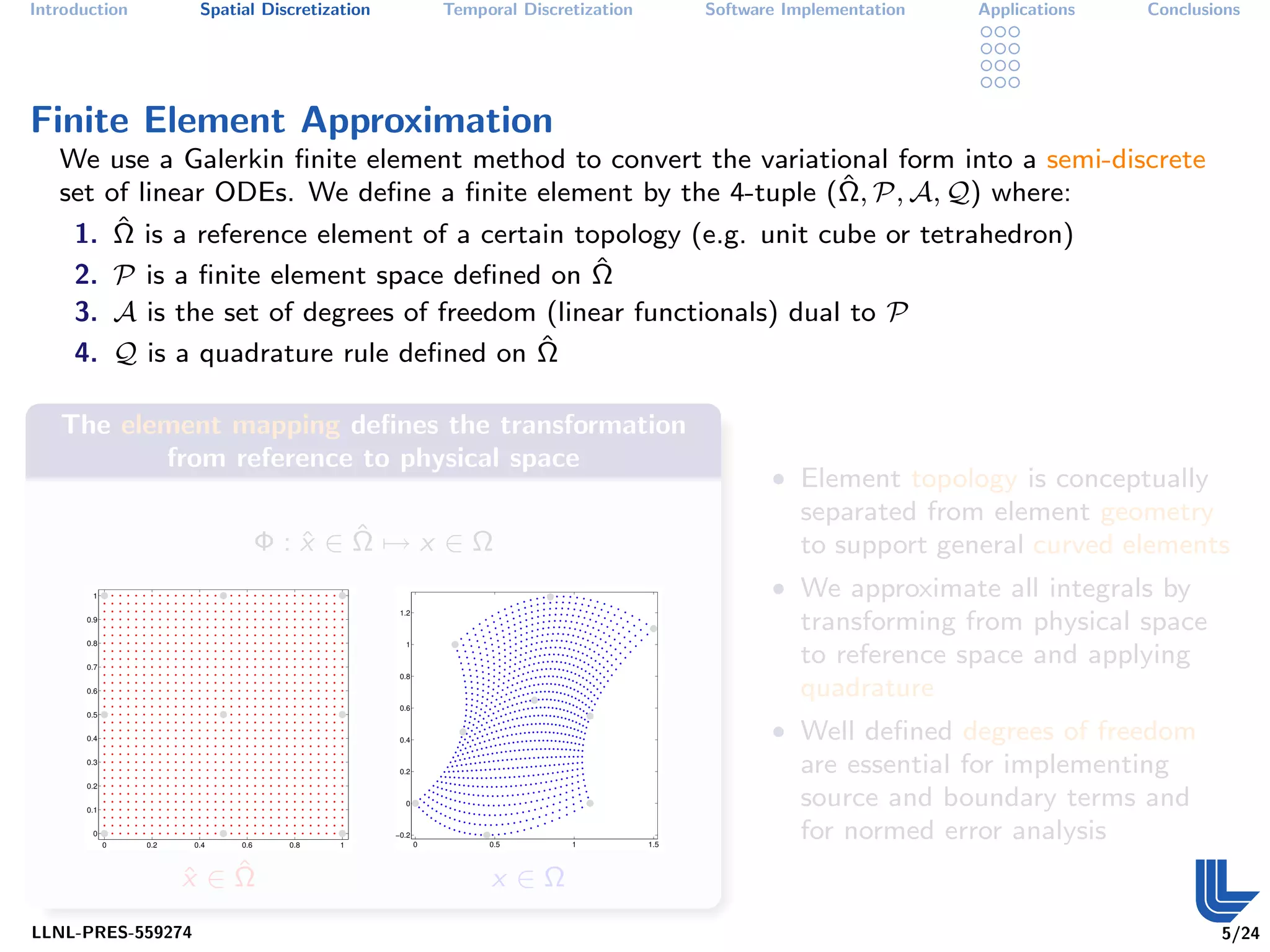
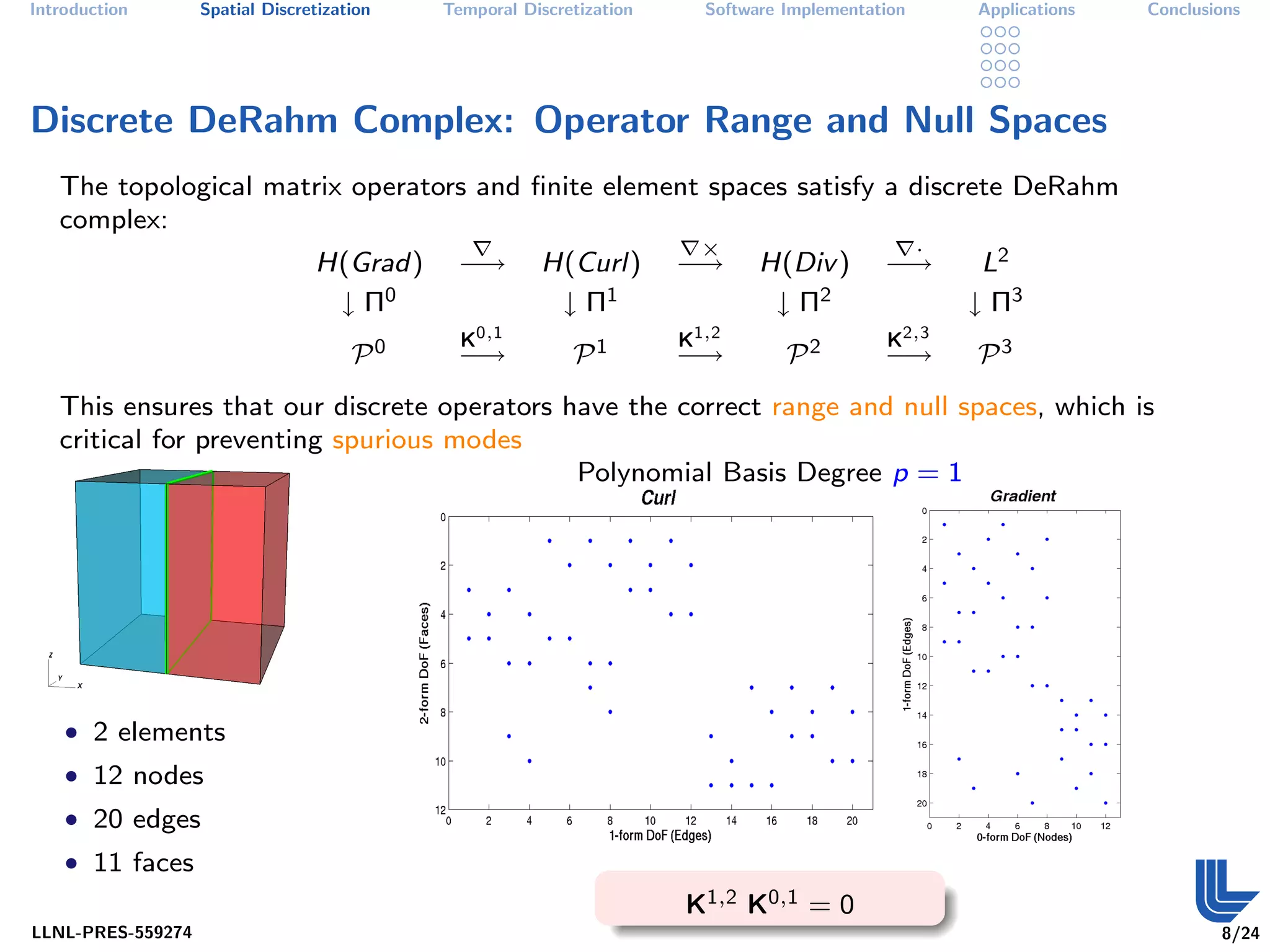
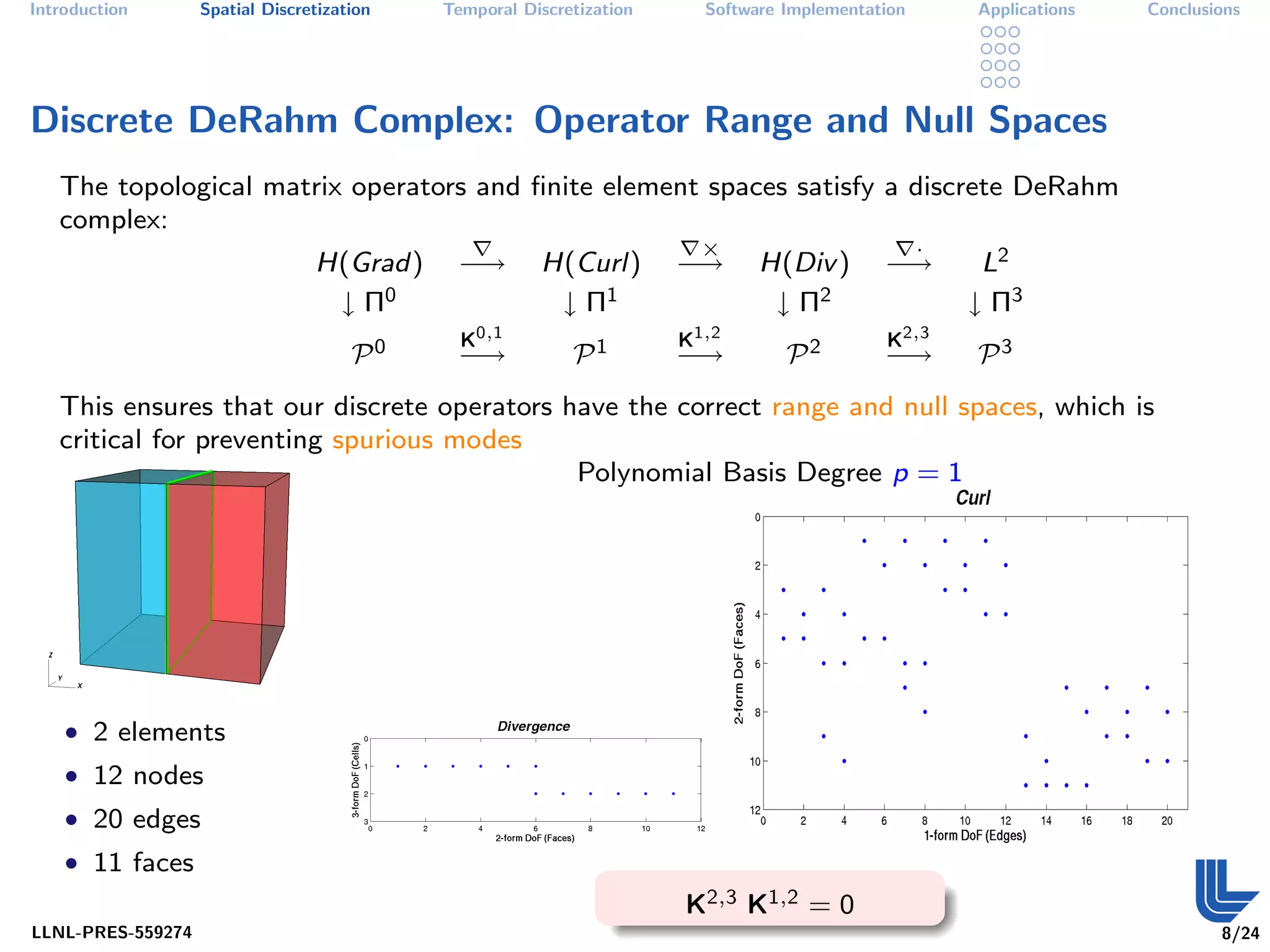
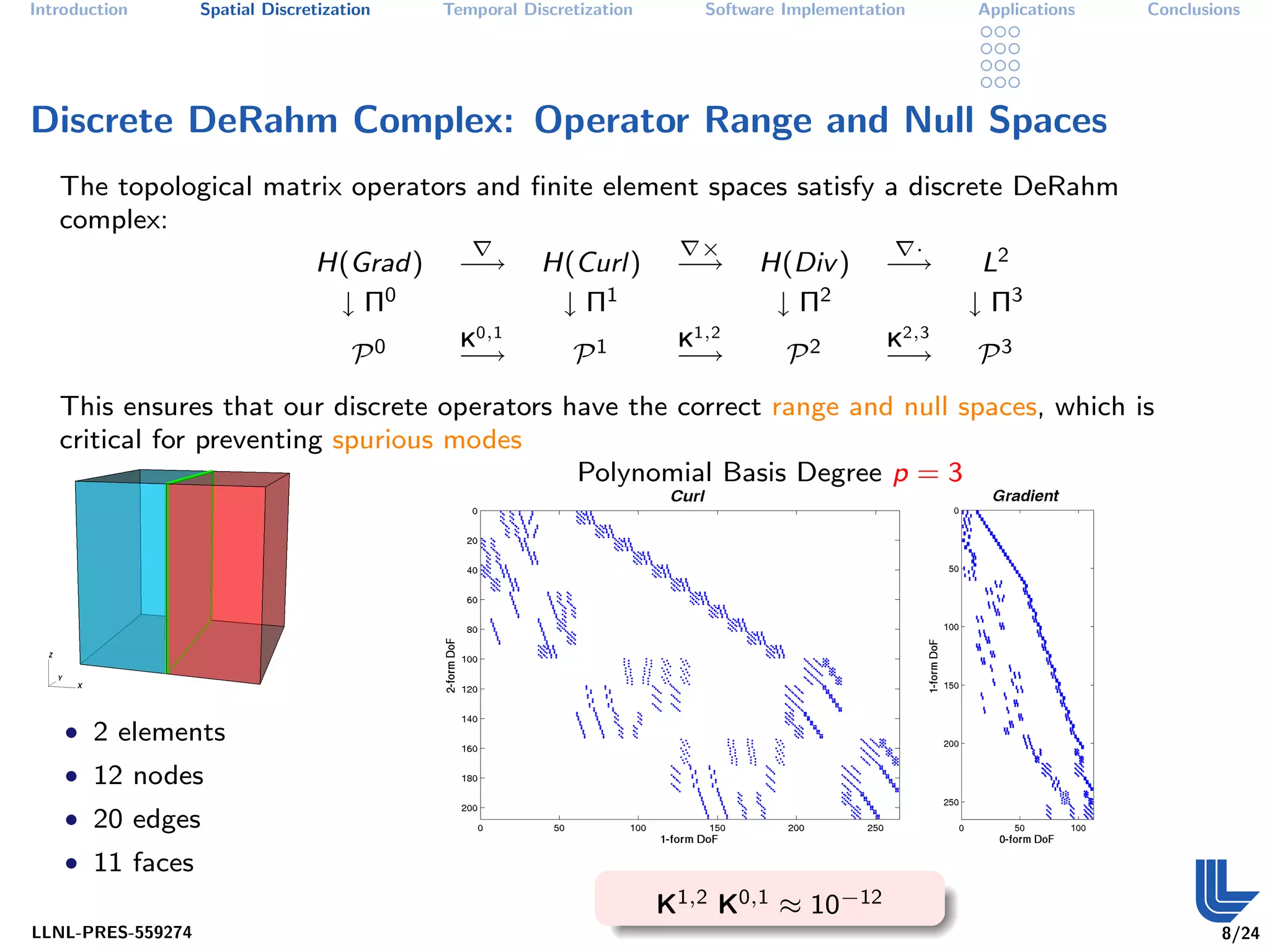
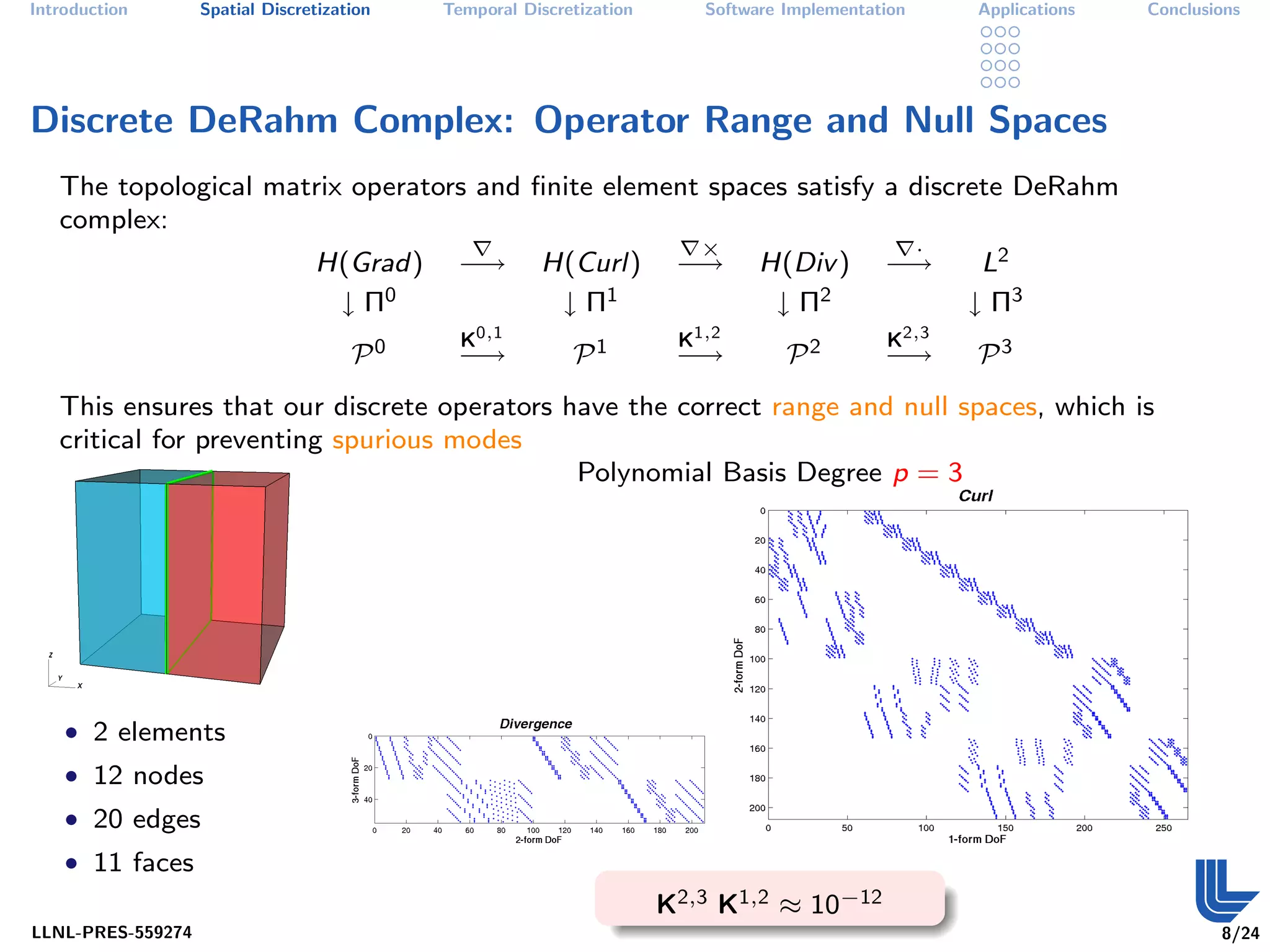
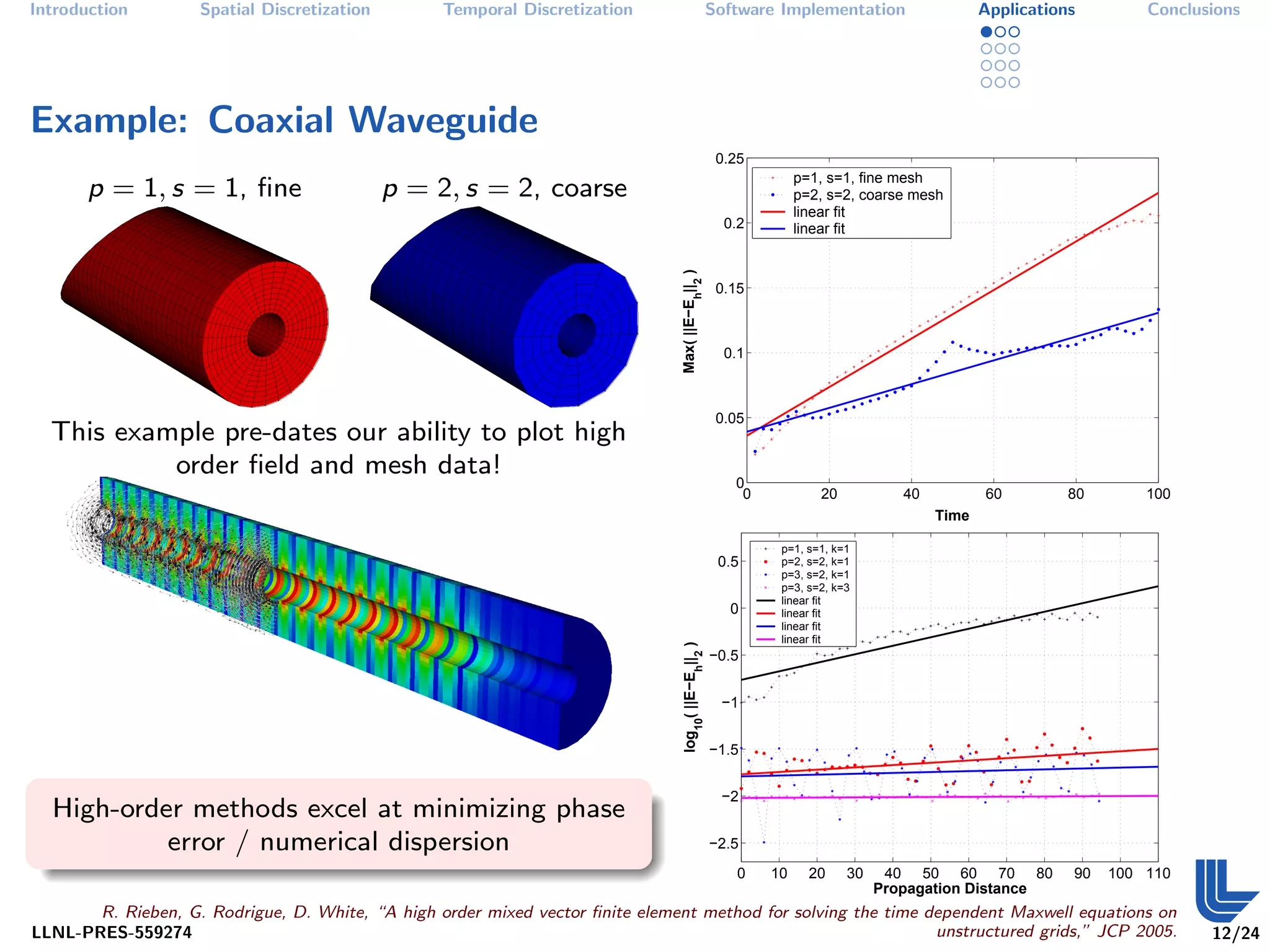
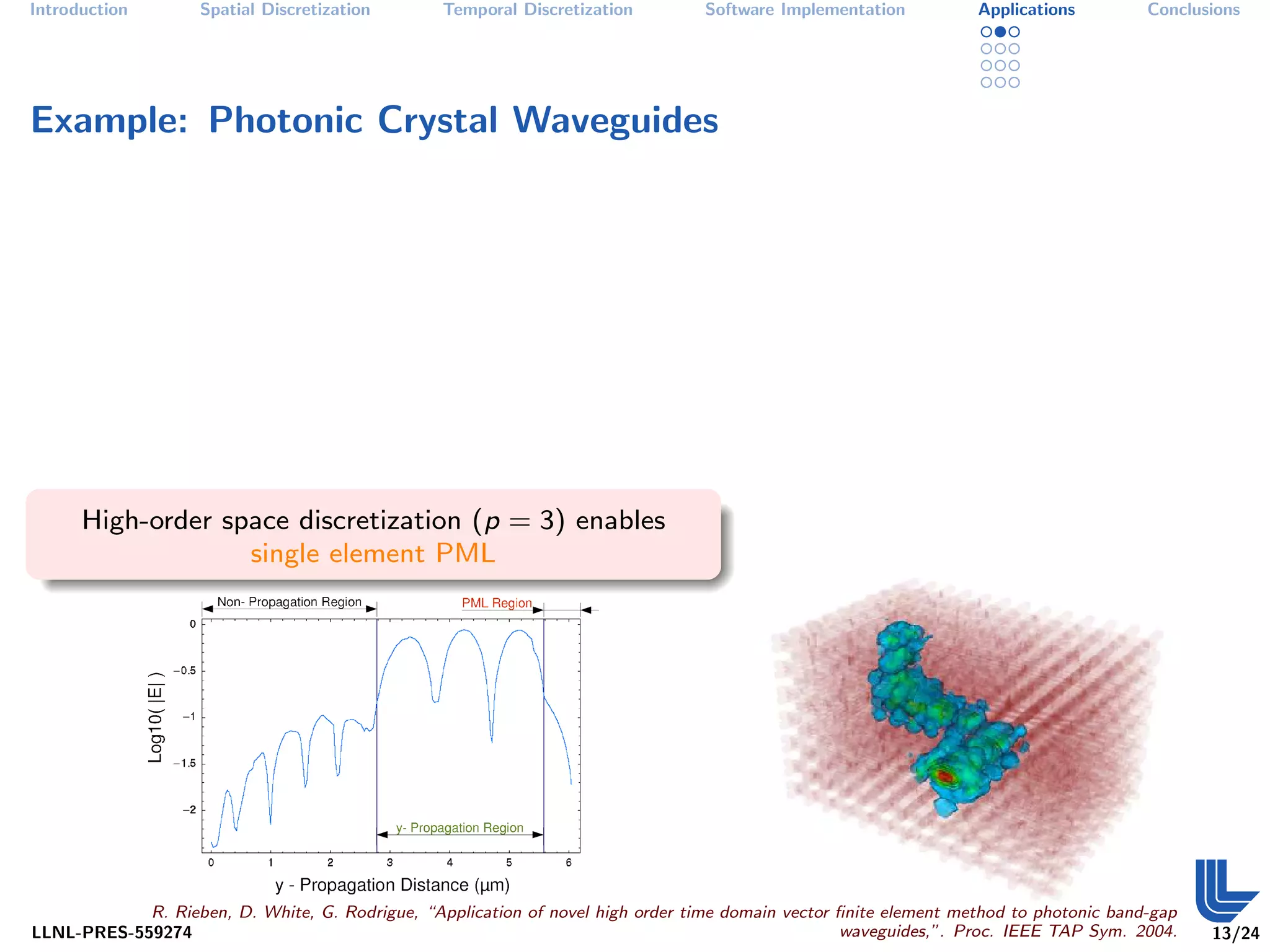
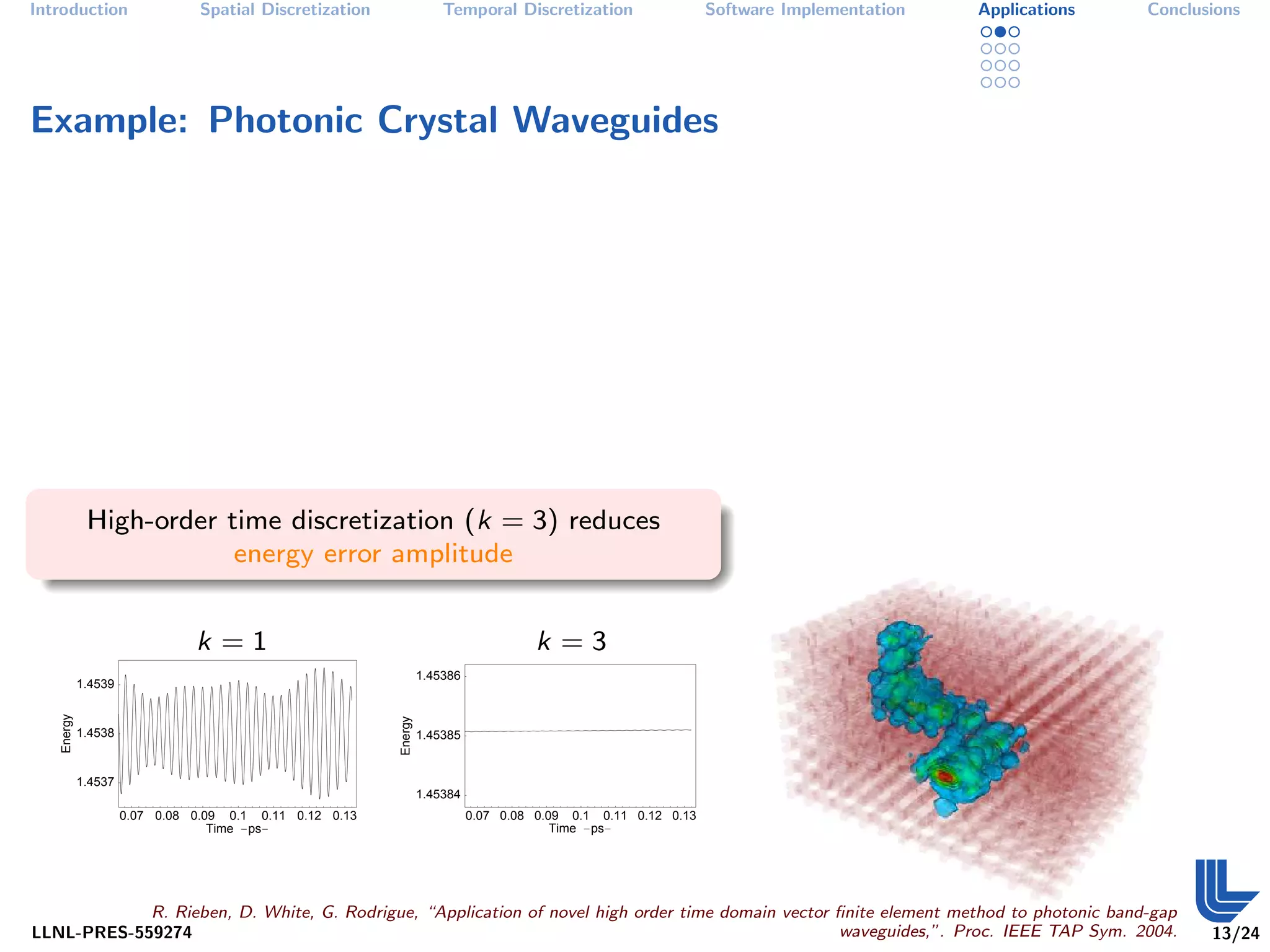
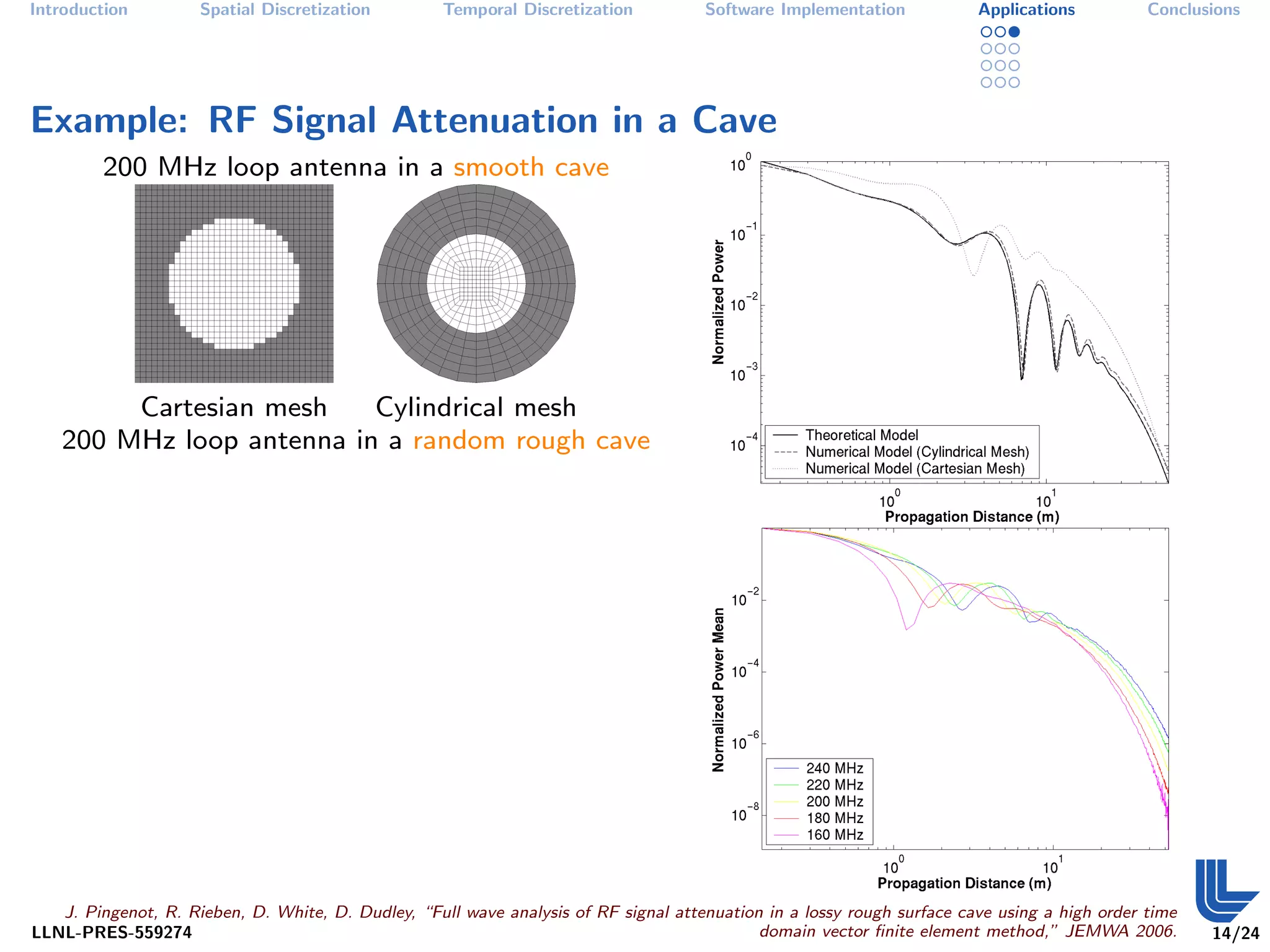
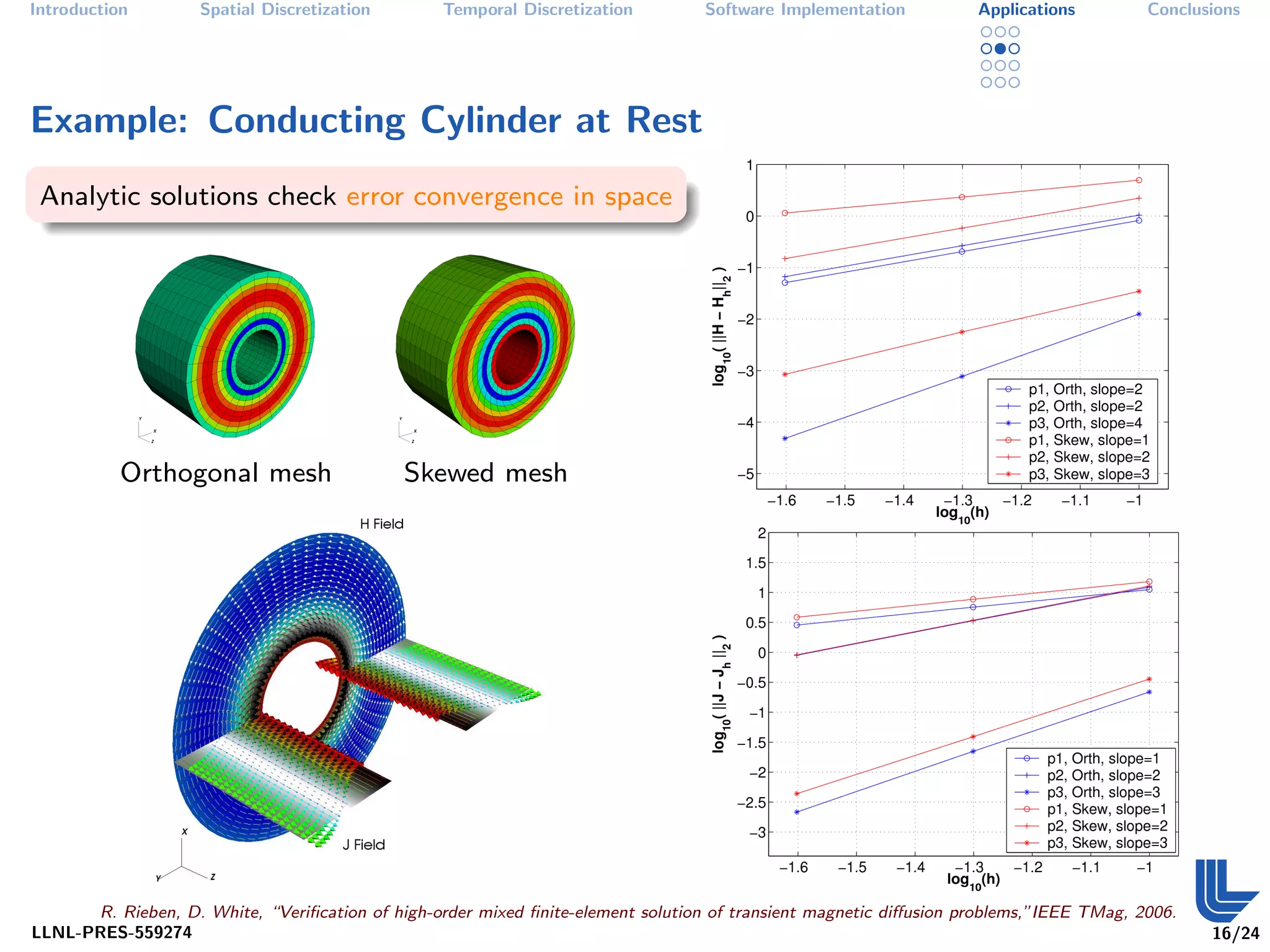
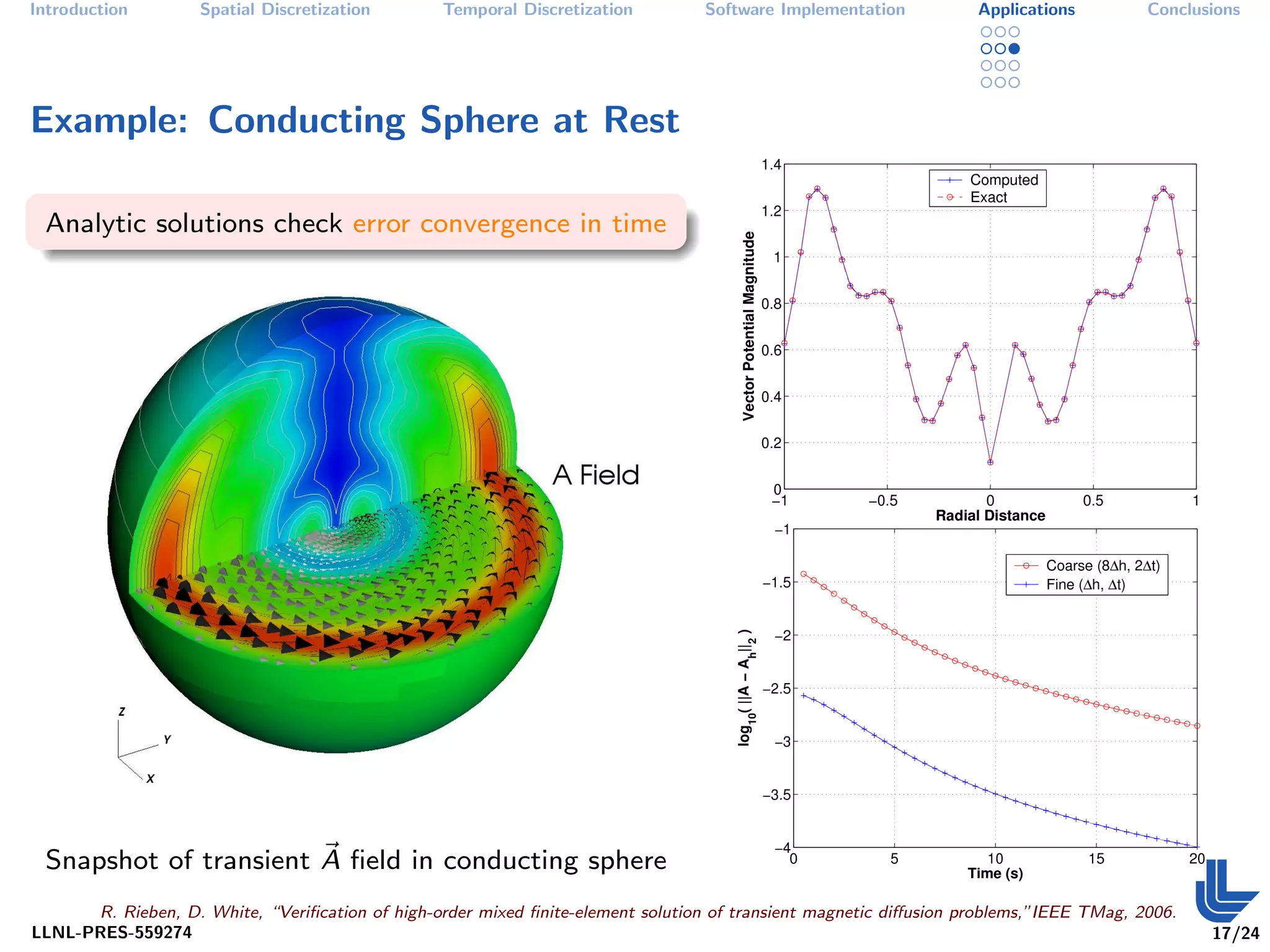
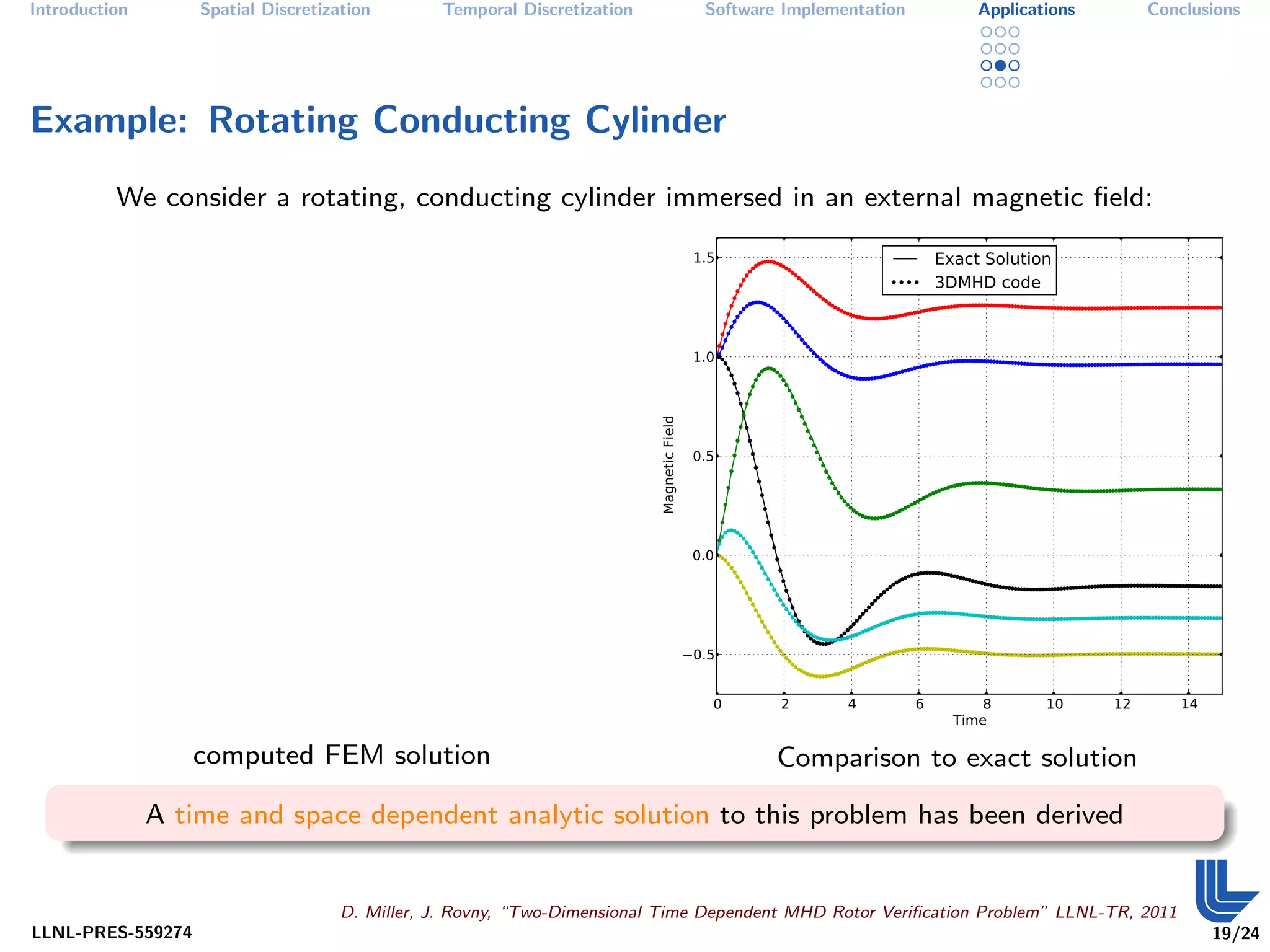
The document discusses high order finite element methods for computational physics from Lawrence Livermore National Laboratory's perspective. It introduces the weak variational formulation of partial differential equations, finite element approximation using a Galerkin method, and the use of discrete differential forms and basis functions to represent solutions. The goal is to develop robust, modular software for solving multi-physics problems on massively parallel architectures.